f(n) 是第n项的值。

f(1)= 1; f(2) =1;

f(n)= f(n-1) + （n-2)

下面的介绍是我从网上查到了，收益匪浅。

分两步推导：

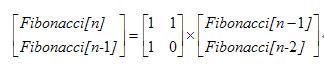
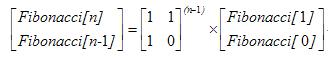
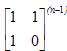   问题的求解就变成 的解决，而幂的求可用二分法来求 

#include <cstdio>
#include <cstdlib>
#include <iostream>
#include <string.h>
#include <algorithm>

using namespace std;
struct matrix
{
	int a[2][2];
};
matrix mul(matrix &x, matrix &y)
{
	matrix res;
	int sum;
	for(int i=0; i<2; i++)
	for(int j=0; j<2; j++)
	{
		sum = 0;
		for(int k=0; k<2; k++)
		sum += x.a[i][k]*y.a[k][j];
		res.a[i][j] = sum;
	}
	x = res;
	return x;
}
matrix pow(matrix x, long e)
{
	matrix ans, temp;
	if(e == 0)
	{
		ans.a[0][0]=1;
		ans.a[0][1]=0;
		ans.a[1][0]=0;
		ans.a[1][1]=1;
		return ans;
	}
	if(e == 1)
	return x;
	temp = pow(x, e>>1);
	ans = mul(temp, temp);
	if(e&1)
	ans = mul(ans,x);
	return ans;
	
}
int main()
{
	int n;
	matrix ans;
	matrix base ={{1,1,1,0}};
	while(~scanf("%d", &n))
	{
		if(!n) printf("0\n");
		else
		{
			ans = pow(base, n-1);
			printf("%d\n",ans.a[0][0]);
		}
	}
system("pause");
return 0;
}