Around the start of the COVID-19 outbreak earlier this year, my friends and I were working out ways to adjust to a life on lockdown. In addition to the physical separation of the quarantine, I had recently accepted a job out-of-state that would require me to move in the coming year, and so it was important for us to find a way to stay in touch over the time and distance.

在今年早些时候爆发COVID-19的前后，我和我的朋友们正在研究适应锁定生活的方法。 除了隔离隔离区外，我最近还接受了一份州外工作，要求我在来年搬家，因此对我们而言，找到一种保持联系的方式很重要和距离。

As an answer to this, I decided to start running a Dungeons and Dragons campaign for my friends. As a varied collection of assorted nerds, this would feed into our collective hobbyist, RPG enthusiast, and geeky natures, and the idea was very positively received by everyone involved.

为此，我决定开始为我的朋友们举办《龙与地下城》战役。 作为各种各样的书呆子，这将使我们的集体业余爱好者，RPG爱好者和怪异的本性得到满足，并且所涉及的每个人都非常满意这个想法。

Setting up the game and running it came with some challenges, which led me to a very interesting mathematical and coding problem, but first, I’ll explain a little about the game.

设置游戏并运行它会遇到一些挑战，这使我遇到了一个非常有趣的数学和编码问题，但首先，我将对游戏进行一些解释。

龙与地下城，掷骰子RPG (Dungeons and Dragons, a Dice-Rolling RPG)

For those of you unfamiliar with D&D, Dungeons and Dragons is a tabletop fantasy role-playing game. Its hallmarks are a group of friends gathering around a table, placing themselves in the shoes of warriors and wizards to go on adventures, undergo quests, and explore dungeons. The game is run and organized by a single person, the Game Master(GM) and the “players” create characters that they use for role-play, combat, exploration, etc.

对于不熟悉D＆D的人来说，Dungeons and Dragons是一款桌上型幻想角色扮演游戏。 它的标志是一群朋友围坐在一张桌子旁，将自己置于战士和巫师的鞋子里，进行冒险，进行任务和探索地牢。 该游戏由一个人运行和组织，Game Master(GM)和“玩家”创建他们用于角色扮演，战斗，探索等的角色。

The game is very open in how it’s played, but one factor is consistent across the majority of rulesets; outcomes and results in the game are decided by dice rolls taking the notation of nds, with n being the number of die to roll and s being the number of sides of each die.

游戏的玩法非常开放，但其中一个因素在大多数规则集中是一致的。 游戏中的结果和结果由掷骰子决定，掷骰子使用n d s表示 ，其中n是掷骰数， s是每个骰子的边数。

For example, in combat the success or failure of an attack might be determined by a roll of 1d20, or one twenty-sided die. The higher the role, the more likely you are to successfully hit something. Similarly, multiple dice can be used. For the damage of a certain spell, the rules may ask you to roll 3d8, which simply means roll three eight-sided die, and the damage you do is the sum of these results.

例如，在战斗中，攻击的成败可能取决于1d20掷骰或二十面骰。 角色越高，您成功击中某事的可能性就越大。 类似地，可以使用多个骰子。 对于某种咒语的伤害，规则可能会要求您掷出3d8，这仅意味着掷出三个八面骰子，而您造成的伤害是这些结果的总和。

As the GM of our game session, the responsibilities of building the world that my players would explore fell to me. This includes writing the story, creating the non-player characters, and perhaps most importantly, designing and orchestrating the combat encounters. As a part of this, it is important for me as the GM to create encounters that challenge my players, without sending something at them that just kills them outright in a turn or two.

作为我们游戏环节的总经理，建立玩家可以探索的世界的责任落在了我身上。 这包括编写故事，创建非玩家角色以及最重要的是设计和编排战斗遭遇。 作为这一过程的一部分，对于我来说，作为总经理来说，创造挑战我的玩家的遭遇，而不是向他们发送任何东西，只会在一两个回合中彻底杀死他们是很重要的。

There is a problem with this however. If you follow the rulesets properly, more difficult encounters with higher-level monsters invariably carry a higher risk of accidentally killing off the party. Stronger creatures mean higher die counts and rolls to their damage, and I can’t control the outcome of these rolls without fudging the rules a bit (something you can technically do, but is generally avoided if at all possible).

但是，这有一个问题。 如果您正确地遵守规则集，与更高级别的怪物进行更困难的遭遇总是会带来更高的意外杀死党的风险。 更强的生物意味着更高的死亡次数和掷骰次数，并且如果不对规则稍加改动，我将无法控制掷骰的结果(从技术上讲是可以做的，但是如果可能的话，通常可以避免这样做)。

So I started looking into the nature of dice rolls, and the way that their outcomes are distributed across various combinations. If I wanted to avoid falsifying dice rolls, I instead had to work with the likelihood of die outcomes and design encounters that maybe looked more difficult than they actually were. To do this, let’s talk about dice roll outcomes and statistics.

因此，我开始研究掷骰子的性质以及其结果在各种组合中的分配方式。 如果我想避免伪造掷骰，我反而不得不将工作与模成果和设计的遭遇，也许看上去比实际更困难的可能性。 为此，我们来谈谈骰子掷骰结果和统计数据。

模具结果的分布 (Distributions of Die Outcomes)

Let’s say I know that my most delicate player has a max health of 22. Through various manipulations, I can balance an encounter around having creatures with only a 5% chance of taking them out in one shot, while also consistently being able to do around 60–80% of their health in a single hit. In this way, I guarantee that my players will feel challenged and most likely terrified by what I throw at them, while also avoiding the potentially un-fun outcome of being taken out in the first turn and not being able to contribute to an encounter at all.

假设我知道我最精巧的玩家的最大生命值是22。通过各种操作，我可以平衡一次拥有生物的机会，一次只有5％的几率将其淘汰，同时也能够始终做到一次击中其健康的60–80％。 这样，我保证我的球员会感到挑战，并且很可能会被我扔给他们的东西吓坏，同时还避免了在第一回合被淘汰并在比赛中无助于贡献的潜在的无趣结果。所有。

To understand this, let’s look at die distributions. As common sense would dictate, rolling any fair die will result in each side coming up approximately the same number of times (randomness doesn’t actually work that way necessarily, but that’s a different article). Below is a probability distribution for one twenty-sided die:

为了理解这一点，让我们看一下模具分布。 就像常识所表明的那样，滚动任何合理的死机将导致每边出现大约相同的次数(随机不一定会那样工作，但这是另一篇文章)。 下面是一个二十面骰子的概率分布：

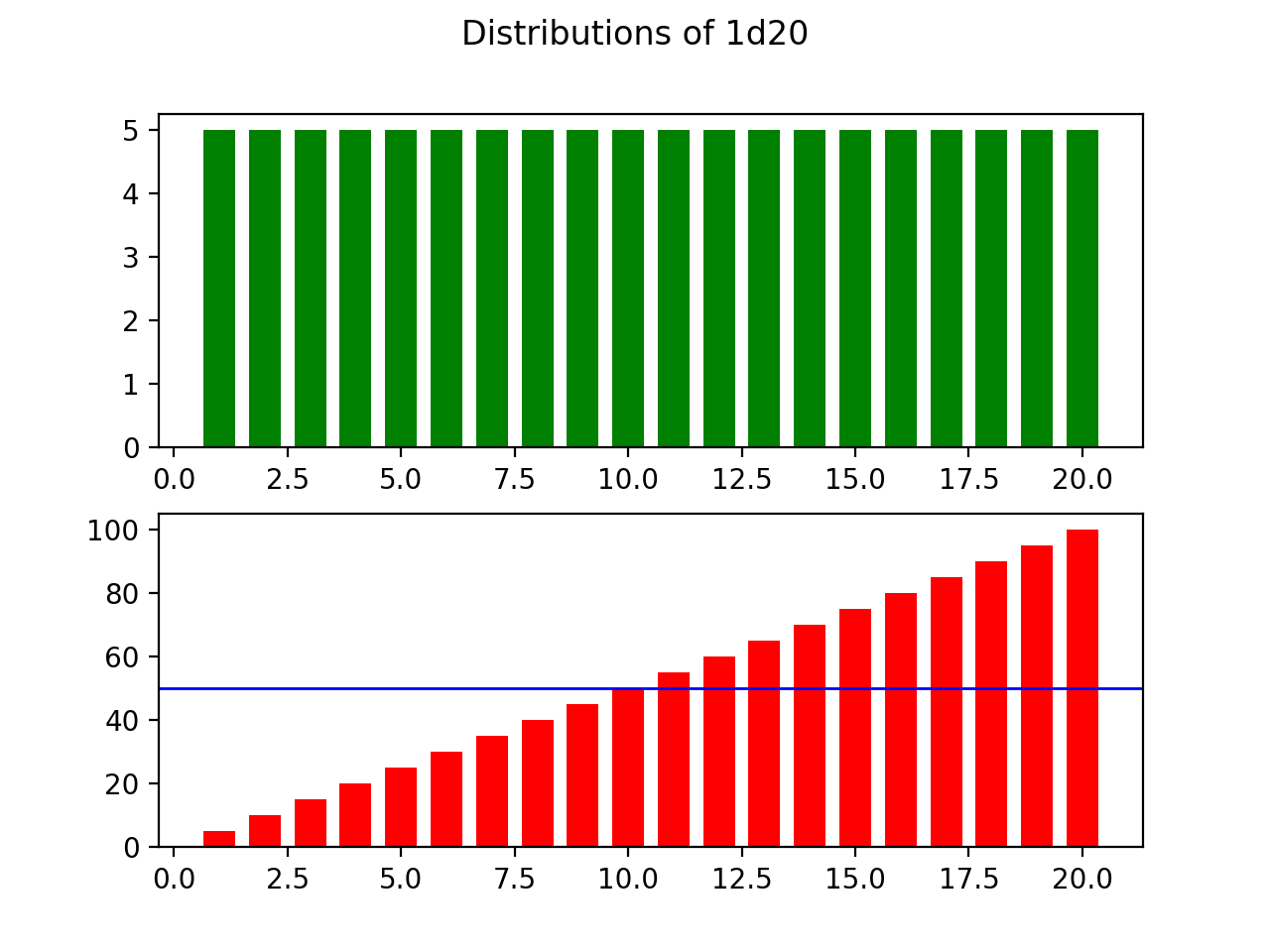
If we think about this distribution in terms of damage, a player could take anywhere between 1 and 20 damage, taking an average of 10.5 damage. But the variance here is as high as it can possibly be. On any given roll, a player is as likely to take 20dmg as they are to take 10dmg or even 1dmg. This inconsistency might be sought after in some cases, but there are ways to represent similar ranges with more consistent results.

如果我们从伤害的角度考虑这种分布，玩家可能会受到1到20伤害之间的任何伤害，平均受到10.5伤害。 但是，这里的差异尽可能大。 在任何给定的掷骰中，玩家服用20毫克的可能性和服用10毫克甚至1毫克的可能性一样。 在某些情况下，可能会寻求这种不一致的地方，但是有一些方法可以表示相似范围的结果更为一致。

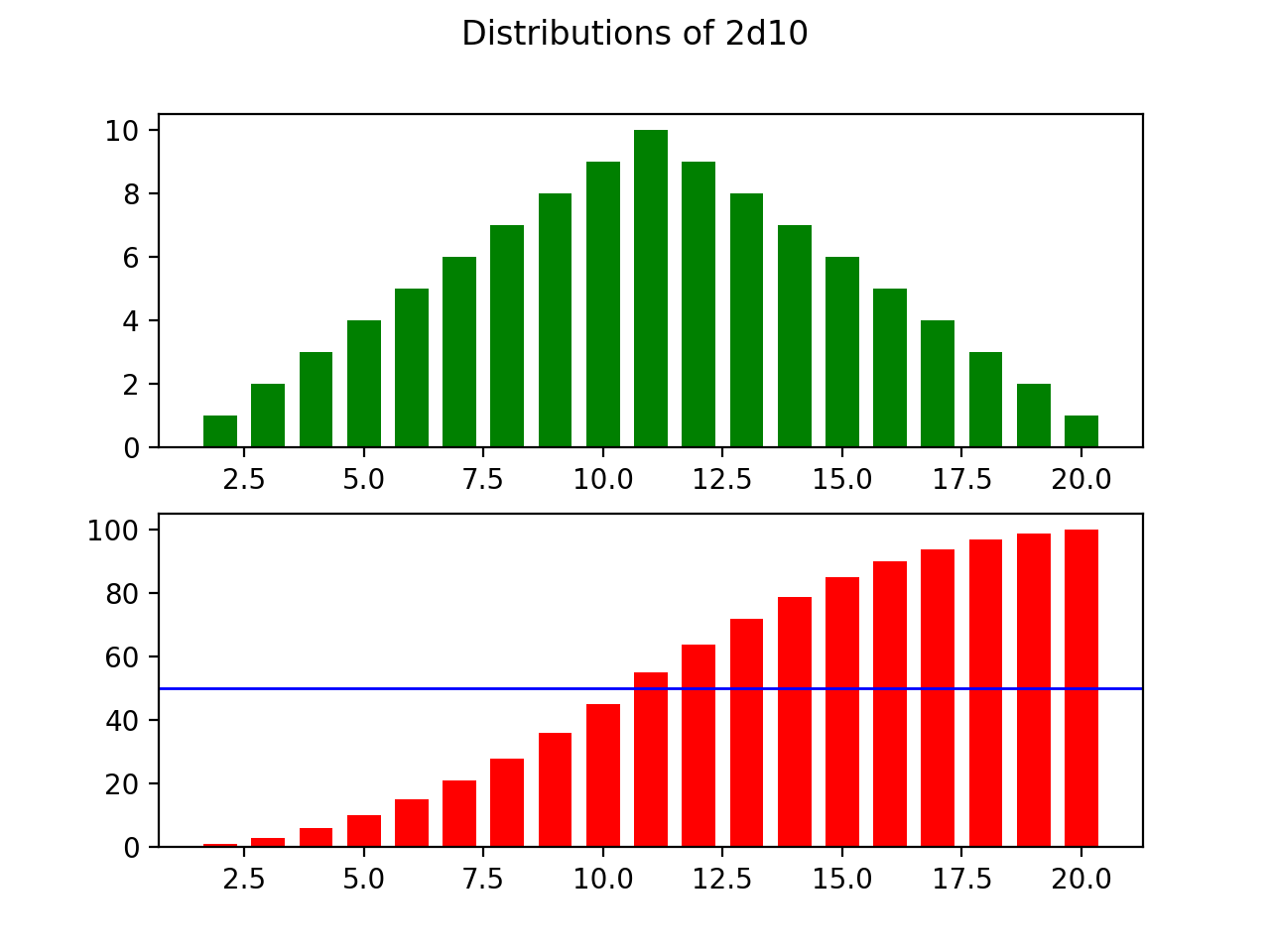
This distribution above shows a slightly different range of 2–20, but the outcomes much more consistently hover around the average. In this scenario, the odds of rolling max damage of 20 and min damage of 2 have dropped from 5% to just under 1% odds. Furthermore, the result of the approximate average of 11 has gone from a 5% odds to just under 10%, almost double the likelihood. Similarly, the values flanking the average have also seen their odds jump.

上面的分布显示2-20的范围略有不同，但是结果更加一致地徘徊在平均值附近。 在这种情况下，最大滚动伤害为20，最小伤害滚动为2的几率已从5％降至不到1％。 此外，大约11的平均值的结果已从5％的几率降至不到10％，几乎是可能性的两倍。 同样，位于平均值两侧的值也出现了几率上升。

As it turns out, in dice rolling, the greater the number of dice that you roll compared to the number of sides on the die, the more closely the distribution approximates a normal distribution with discrete values. To show this, observe what happens when we maintain the number of sides on the die, but repeatedly increase the number rolled:

事实证明，在掷骰子时，与骰子侧面的数量相比，掷骰子的数量越大，分布越接近具有离散值的正态分布。 为了说明这一点，请观察当我们保持模具上的边数但重复增加滚动数时会发生什么：

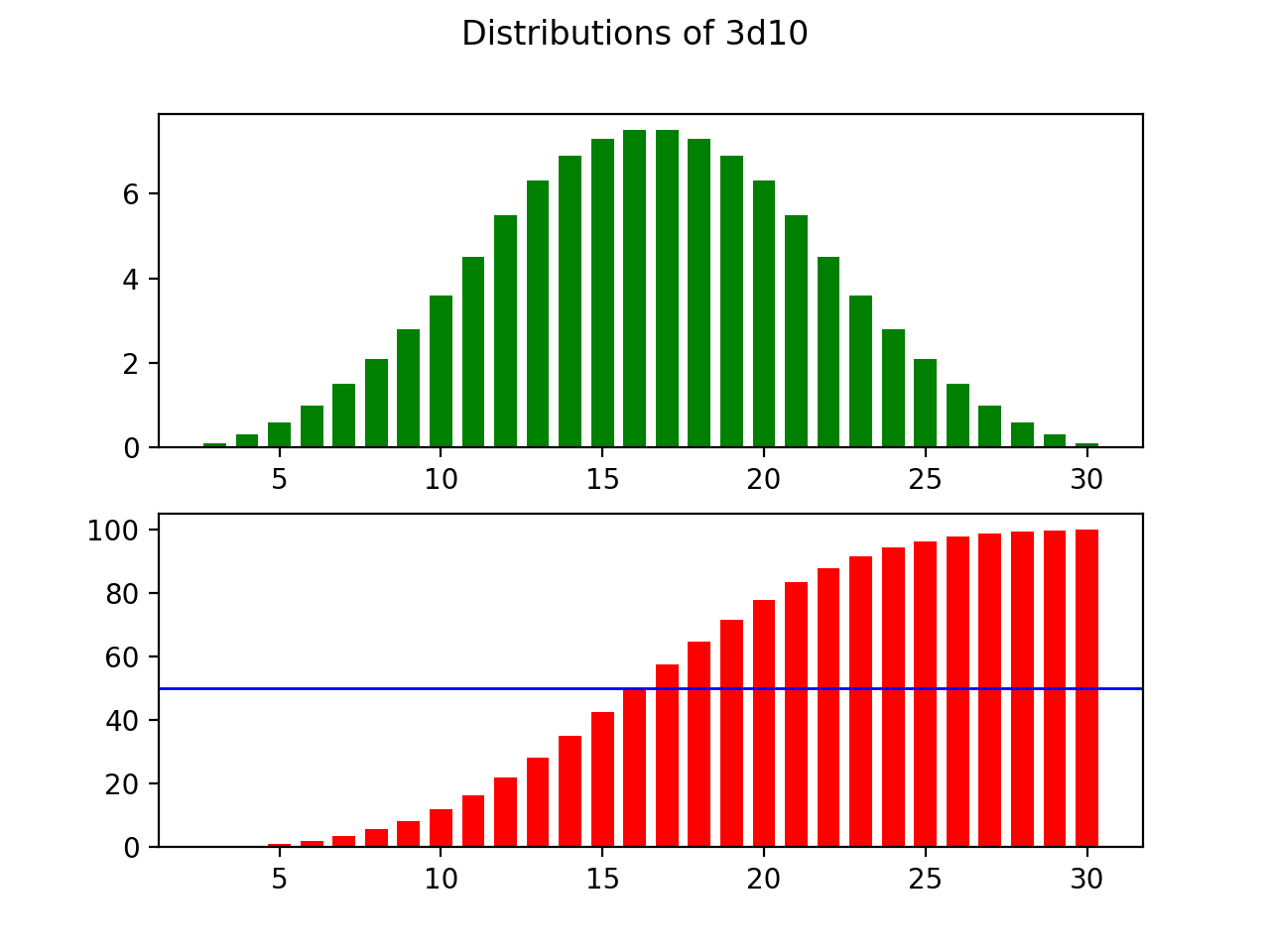
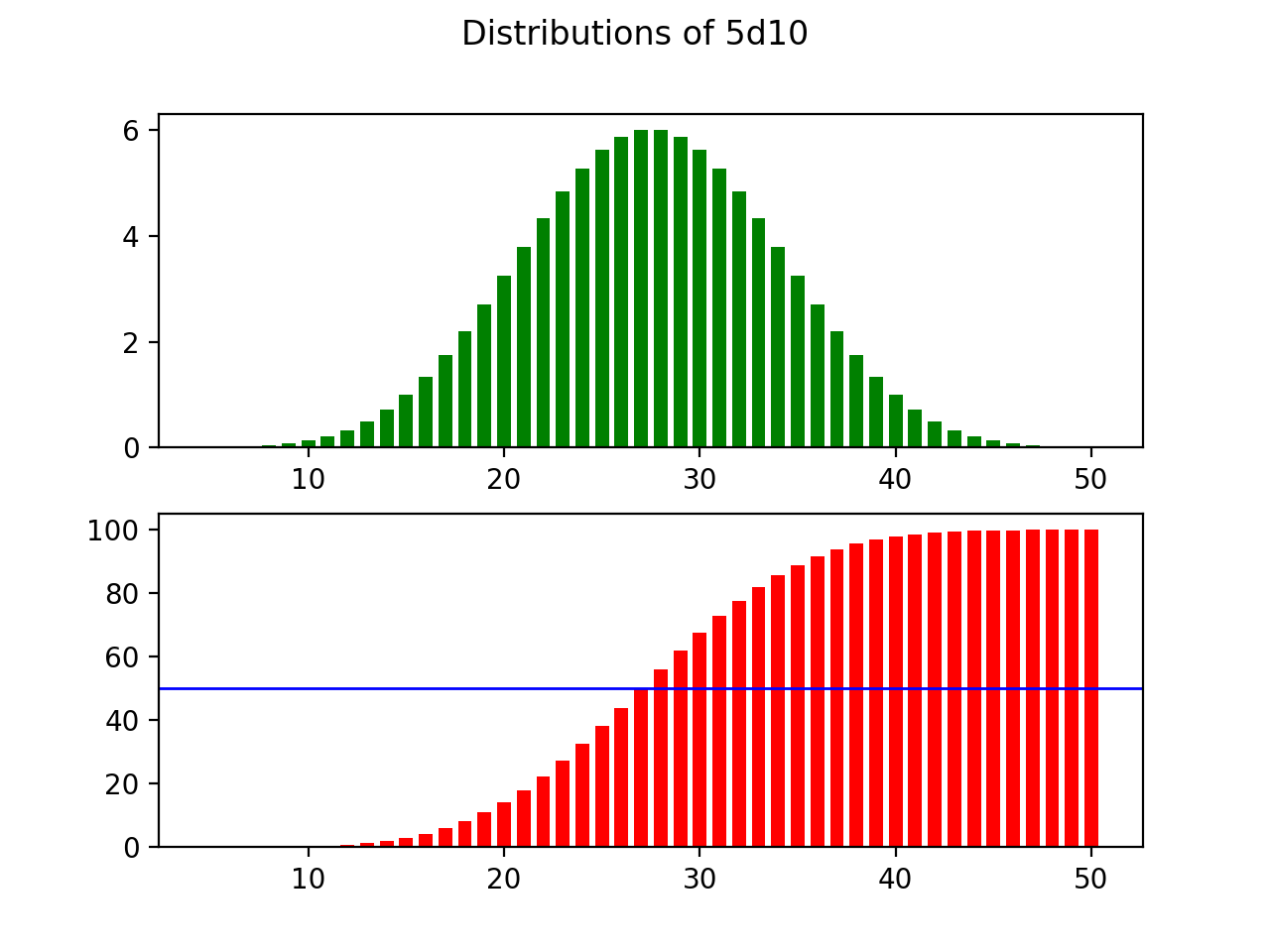
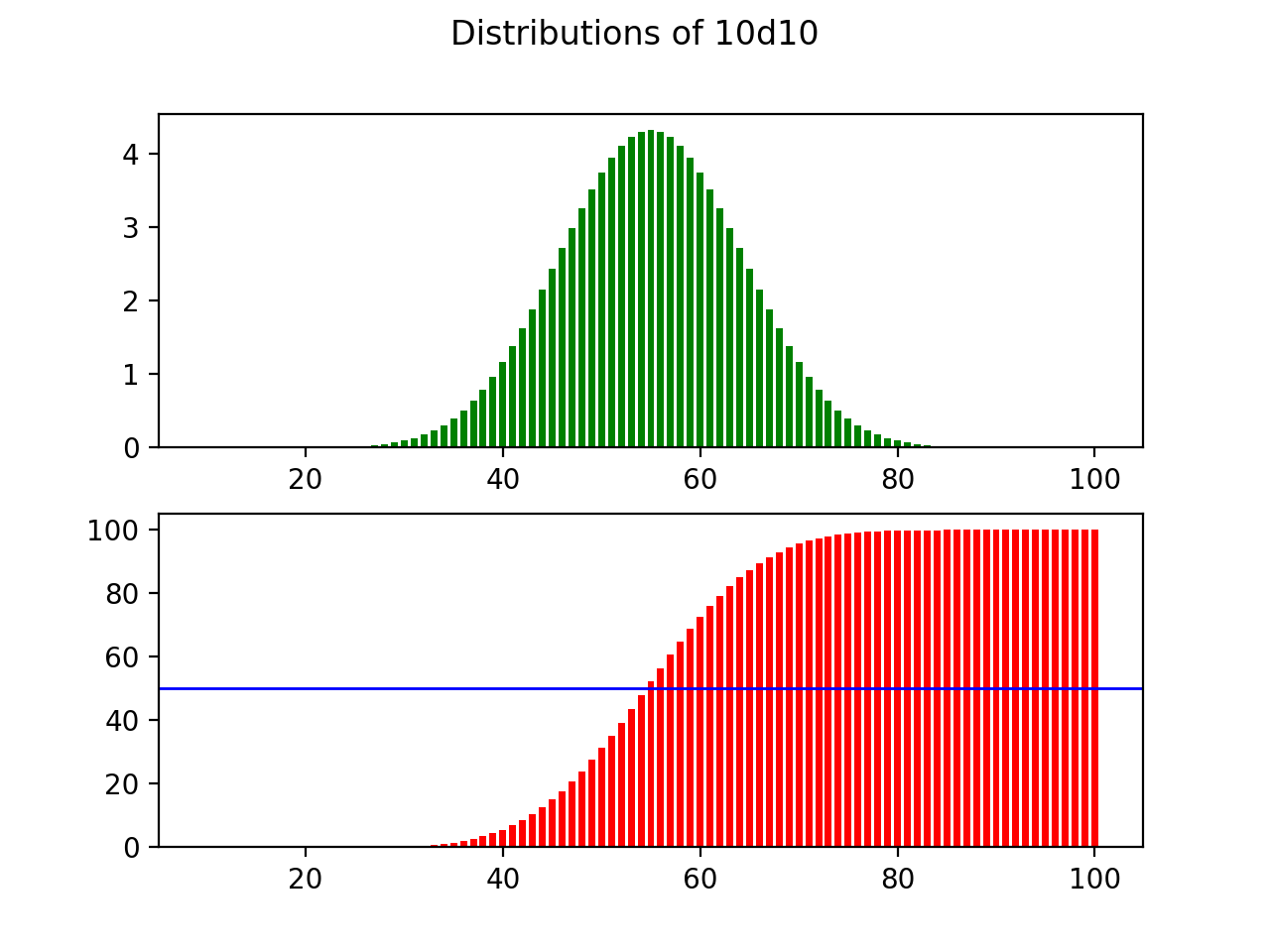
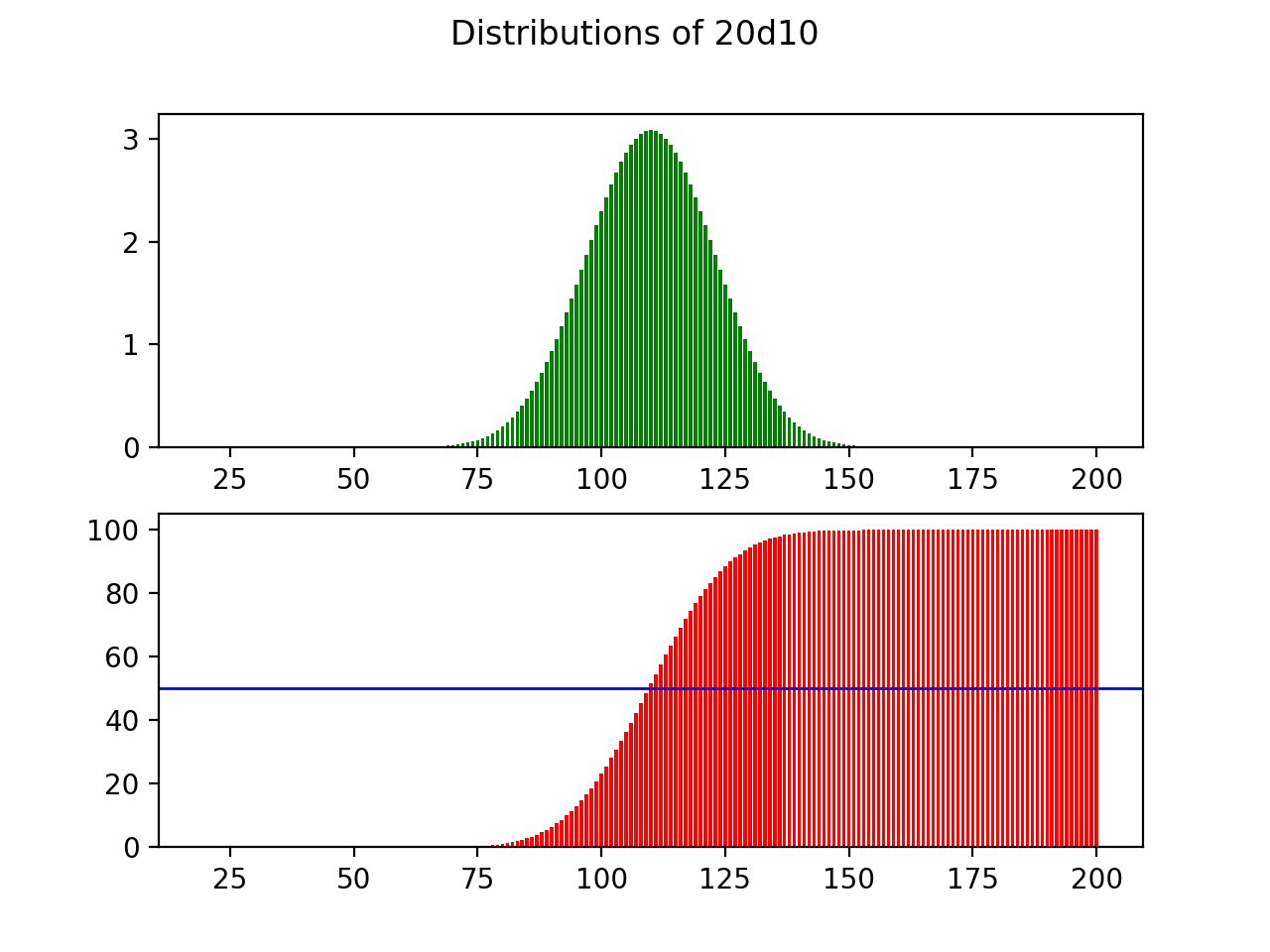
Similarly, there seems to be a direct relationship between this ratio and the standard deviation of the output distribution. A higher number of dice reduces the standard deviation, and the outcomes more strongly cluster around the average. On the other hand, increasing the number of sides on the die increases the standard deviation, and spreads the outcome to make the extremes more likely.

同样，该比率与输出分布的标准偏差之间似乎存在直接关系。 更高数量的骰子可减少标准偏差，并且结果在平均值附近更加集中。 另一方面，增加芯片上的边数会增加标准偏差，并扩展结果以使极端情况更可能发生。

Understanding these concepts makes it surprisingly easy to design encounters that run much more consistently with what you as the engineer have in mind, while still providing the illusion of randomness and the “just-good-enough” roll that feels so satisfying to play. Players can take near-fatal blows that just miss killing them, without realizing that your manipulations make the odds of a near-fatal blow about 90%, while the odds of an actually fatal blow lie below 2%.

理解了这些概念后，就可以轻松设计出与工程师想像的一致的运行体验，同时仍然提供随机感和“玩够了”的感觉。 玩家可能遭受致命的打击，只是错过了杀死它们的机会，而没有意识到您的操作使致命打击的几率约为90％，而实际致命打击的几率低于2％。

This understanding greatly helped me improve the quality of my games, as I could design encounters that felt threatening and kept my players on their toes. Encounters that challenged them to think and plan with real danger in the midst. At the same time, I’m able to avoid a game-breaking snowball, where one of my players dies from the outset, and a fight planned for five people is now only four strong.

这种理解极大地帮助我提高了游戏质量，因为我可以设计遇到威胁的比赛并让球员保持警惕。 遇到挑战的人在中间遇到真正的危险进行思考和计划。 同时，我能够避免打破常规的雪球，我的一名球员从一开始就死于一场比赛，而计划中的五个人的战斗现在只有四个人。

With this new understanding at hand, I decided to generate a toolkit to help me produce these distributions. I wanted a way to plug in these die rolls and print a distribution output so I could easily see how likely I was to kill my players.

有了这种新的理解，我决定生成一个工具包来帮助我生成这些发行版。 我想要一种插入这些骰子并打印分配输出的方法，这样我就可以很容易地看出我杀死玩家的可能性。

As it turns out, this problem was more difficult than I originally thought.

事实证明，这个问题比我最初想的要困难。

产生模具结果并快速完成 (Generating Die Outcomes, and Doing it Fast)

I chose to approach this problem in the same language that I do most of my quick scratch-work: Python. Python has the benefit of already containing a large online repo of math-based libraries, and given the ease of coding in it, I figured it was a good place to start.

我选择使用与我大部分快速工作相同的语言来解决此问题：Python。 Python的好处是已经包含了大量在线的基于数学的库，并且考虑到其中的编码简便性，我认为这是一个不错的起点。

I started this approach the way a lot of people start a lot of problems. The good-ol’ brute force method! With the help of my good friend Kyle Silver (who is substantially better at abstract math than me), we made an algorithm to generate all possible outcomes of n rolls of s sided die through a clever mathematical trick.

我以很多人开始遇到很多问题的方式开始了这种方法。 善意的蛮力法！ 随着我的好朋友凯尔银(谁大大改善是在抽象的数学比我)的帮助下，我们做了一个算法生成的n个 S的卷通过巧妙的数学技巧面的骰子所有可能的结果。

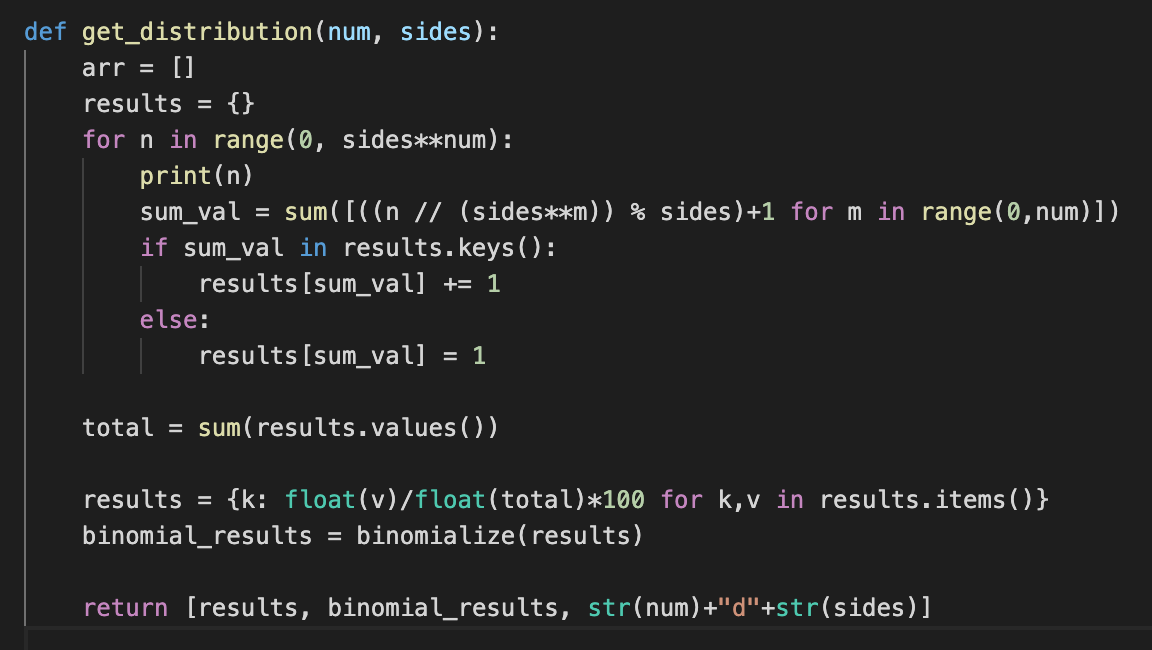
The way this algorithm works is as follows:

该算法的工作方式如下：

1. First, we figure out how many possible outcomes of die rolls there are and iterate through these in a loop (for n in range(0,sides**num))

   首先，我们找出模辊的可能结果，并循环遍历这些结果(对于n在range(0， 侧面 ** num )中)

2. Next, for each number, we represent the number in mod base => #sides. For example, in mod 4, 10 would be represented as 22.

   接下来，对于每个数字，我们用mod base =>＃ 侧面表示数字。 例如，在mod 4中，10将表示为22。

3. Last, for each number, we chop off digits num number of times, and add 1 to each digit. This represents a single die outcome in the roll.

   最后，对于每个数字，我们将数字num斩除一次，然后在每个数字上加1。 这代表了掷骰的结果。

This produces the effect of generating all outcomes of n rolls by counting from 0 to the number of expected outcomes in mod base of the number of die sides. This is probably better explained with an example…

通过从0到以模具边数为基数的期望结果数进行计数，这产生了生成n卷所有结果的效果。 用一个例子可以更好地解释这一点……

Say I roll 2d3, or two three-sided die. The number of possible outcomes for this combination is 2³ or 8 possible outcomes. To generate the number of outcomes, we count from 0 to 8 in base 3 with two digits, which looks like this:

假设我掷2d3或两个三面骰。 此组合可能产生的结果数为2³或8个可能的结果。 为了生成结果数，我们以2为基数从0到8进行计数，如下所示：

1. 0 = 00 => (1,1)
   0 = 00 =>(1,1)
2. 1 = 01 => (1,2)
   1 = 01 =>(1,2)
3. 2 = 02 => (1,3)
   2 = 02 =>(1,3)
4. 3 = 10 => (2,1)
   3 = 10 =>(2,1)
5. 4 = 11 => (2,2)
   4 = 11 =>(2,2)
6. 5 = 12 => (2,3)
   5 = 12 =>(2,3)
7. 6 = 20 => (3,1)
   6 = 20 =>(3,1)
8. 7 = 21 => (3,2)
   7 = 21 =>(3,2)
9. 8 = 22 => (3,3)
   8 = 22 =>(3,3)

As you can see above, with this counting method, we can mathematically generate all possible outcomes of the set of die rolls consistently across any combination of dice. By taking the sums of these resulting digit outcomes, we can generate our distribution. But this algorithm comes with a problem:

如上所示，使用这种计数方法，我们可以在任何骰子组合上以数学方式一致地生成一组掷骰子的所有可能结果。 通过取这些结果数字结果的总和，我们可以生成我们的分布。 但是这个算法有一个问题：

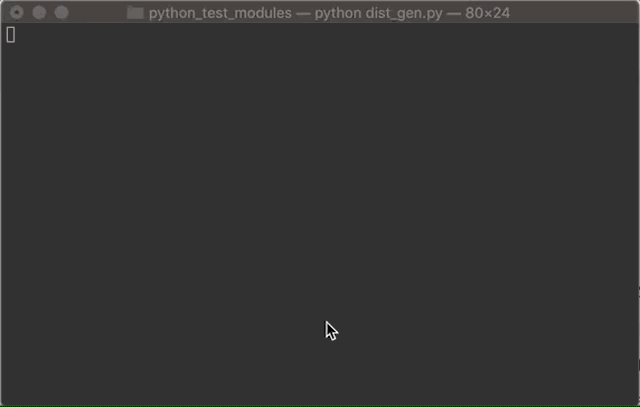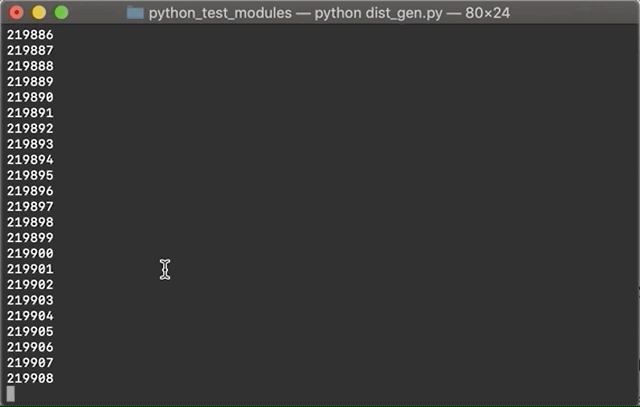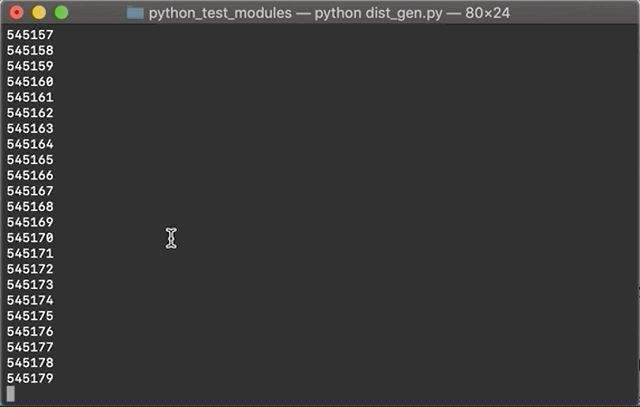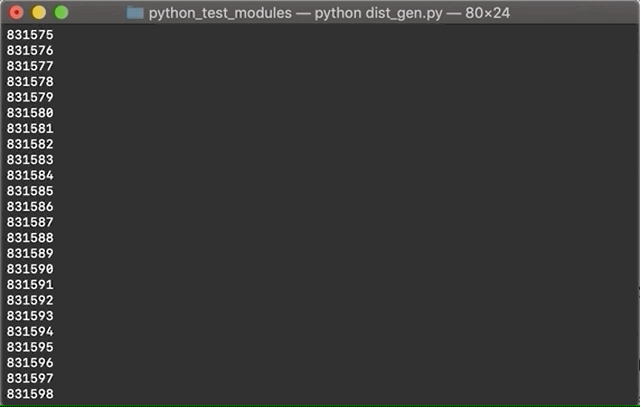
This method is sloooooooooooooow. The example I show above is the algorithm running through a 14d6 calculation, which is the damage for a 9th level Fireball in D&D if anyone is curious. I didn’t test the full runtime of it, but the reason I didn’t take the time is because I projected how long it would take after tracking its pace for about an hour, and it came out to approximately two-weeks of runtime to finish the 14d6 operation. I decided not to wait that long, killed the program, and talked to my buddy Kyle. In his own words, “Hmmm, it could probably use some optimization.”

这种方法是sloooooooooooooow 。 我上面显示的示例是通过14d6计算运行的算法，如果有人好奇，这是D＆D中第9级火球的损害。 我没有测试它的完整运行时间，但是我没有花时间的原因是因为我预测了跟踪它的速度大约一个小时后要花费多长时间，并且它花费了大约两周的运行时间完成14d6操作。 我决定不等那么久，终止该程序，并与我的好友Kyle进行了交谈。 用他自己的话说，“嗯，它可能需要进行一些优化。”

So I poured over the problem for a whole evening, did some research and finally came to a realization. By generating every possible combination of numbers from 1 to [#sides of the die] allowing for duplicates, I could produce a list of all possible number combinations that would appear in a series of die rolls of a certain number of sides. For example in a 3d4 setting, I could generate all combinations as follows:

因此，我整个晚上都在思考这个问题，做了一些研究，最后才意识到。 通过生成从1到[模具的＃面]的每种可能的数字组合(允许重复)，我可以生成所有可能的数字组合的列表，这些列表将出现在一定数量的侧面的一系列模辊中。 例如，在3d4设置中，我可以生成以下所有组合：

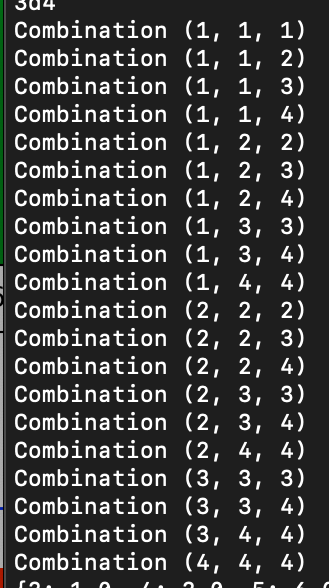
With these combinations, I could generate all possible die roll outcomes as permutations of each set. For example 1,2,4 could be 2,1,4 or 4,2,1, etc. All of these are valid rolls, and the benefit of this method is that the sum of each combination (and thus all of its permutations) would be the same, and I’d only need to calculate it once per combination.

通过这些组合，我可以生成所有可能的冲模结果作为每组的排列。 例如1,2,4可以是2,1,4或4,2,1，依此类推。所有这些都是有效的掷骰，这种方法的好处是每个组合的总和(以及所有组合的排列) )将是相同的，并且我只需要为每个组合计算一次即可。

The downside was twofold. For starters, generating all of the permutations from the combinations was part of the problem in the first algorithm, and tended to be fairly slow. Second, many of the combinations had duplicates, and generating permutations that swapped duplicate values (e.g. 1,1,2 becoming 1,1,2 by ‘swapping’ the 1's, despite the outcome being the same) would have to be checked against and removed, decreasing speed further. But as it turns out, I didn’t need to generate all the permutations of each combination in order to produce the distribution. All I needed to know was how many unique permutations there are for each combination, and increment the sum bin accordingly. As it turns out, there’s a formula just for this:

缺点是双重的。 对于初学者来说，从组合中生成所有排列是第一个算法中问题的一部分，而且往往相当缓慢。 其次，许多组合都具有重复项，并且必须检查生成替换掉重复值的排列(例如，尽管结果相同，但通过“交换” 1将1,1,2变成1,1,2)，并且删除，进一步降低了速度。 但事实证明，我不需要生成每个组合的所有排列即可生成分布。 我只需要知道有多少 每个组合都有唯一的排列，并相应增加求和箱。 事实证明，有一个公式专门用于此：

• (factorial of the length of the set)/(factorials of the duplicates)
  (集合长度的因数)/(重复项的因数)

What this means is that if I have the following combination: (1,1,2,3,4,4,4,5), I have a set of length 8, a duplicate set of length 2, and a duplicate set of length 3. Thus, the total number of unique permutations for this set can be calculated as follows:

这意味着如果我具有以下组合：(1,1,2,3,4,4,4,5)，则我有一组长度8，一组重复的长度2和一组重复的长度3。因此，此集合的唯一排列总数可以计算如下：

8!/(2!3!)

8！/(2！3！)

Essentially, you take the factorial of the length, which is the standard way of determining permutations of a set, and divide out the permutations of the subsets of duplicates. Because of this operation, I no longer had to generate every possible outcome if I just generated every combination and performed a mathematical operation on each. The code came out something like this:

本质上，您采用长度的阶乘(这是确定集合的排列的标准方法)，并划分出重复项子集的排列。 由于此操作，如果我仅生成每个组合并对每个组合执行数学运算，则不再需要生成所有可能的结果。 代码出来是这样的：

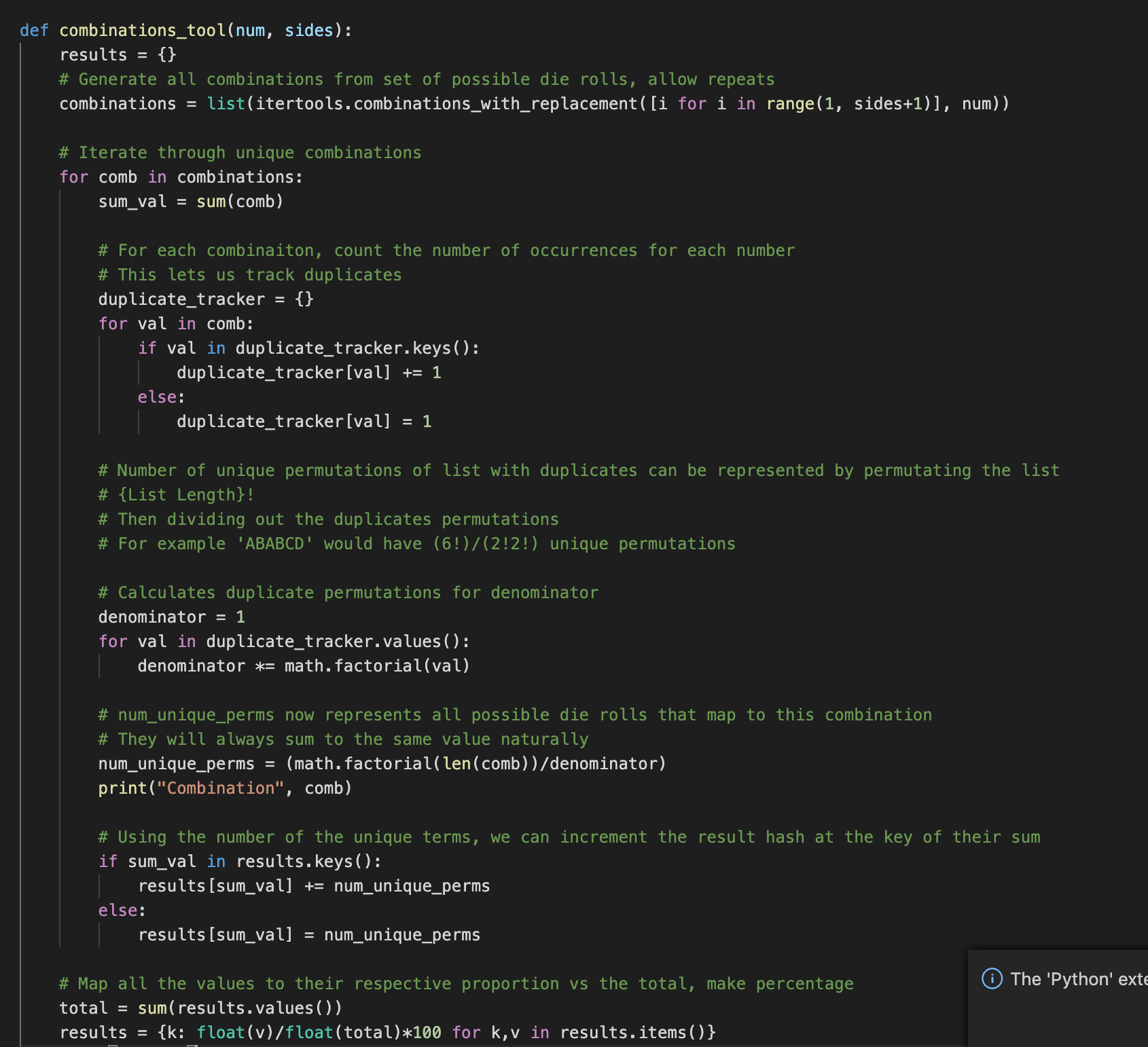
After constructing this method, I wanted to test it on the same set I faced a problem with in the previous algorithm. So I ran it for 14d6…

构建完此方法后，我想在遇到先前算法存在问题的同一集合上对其进行测试。 所以我跑了14d6

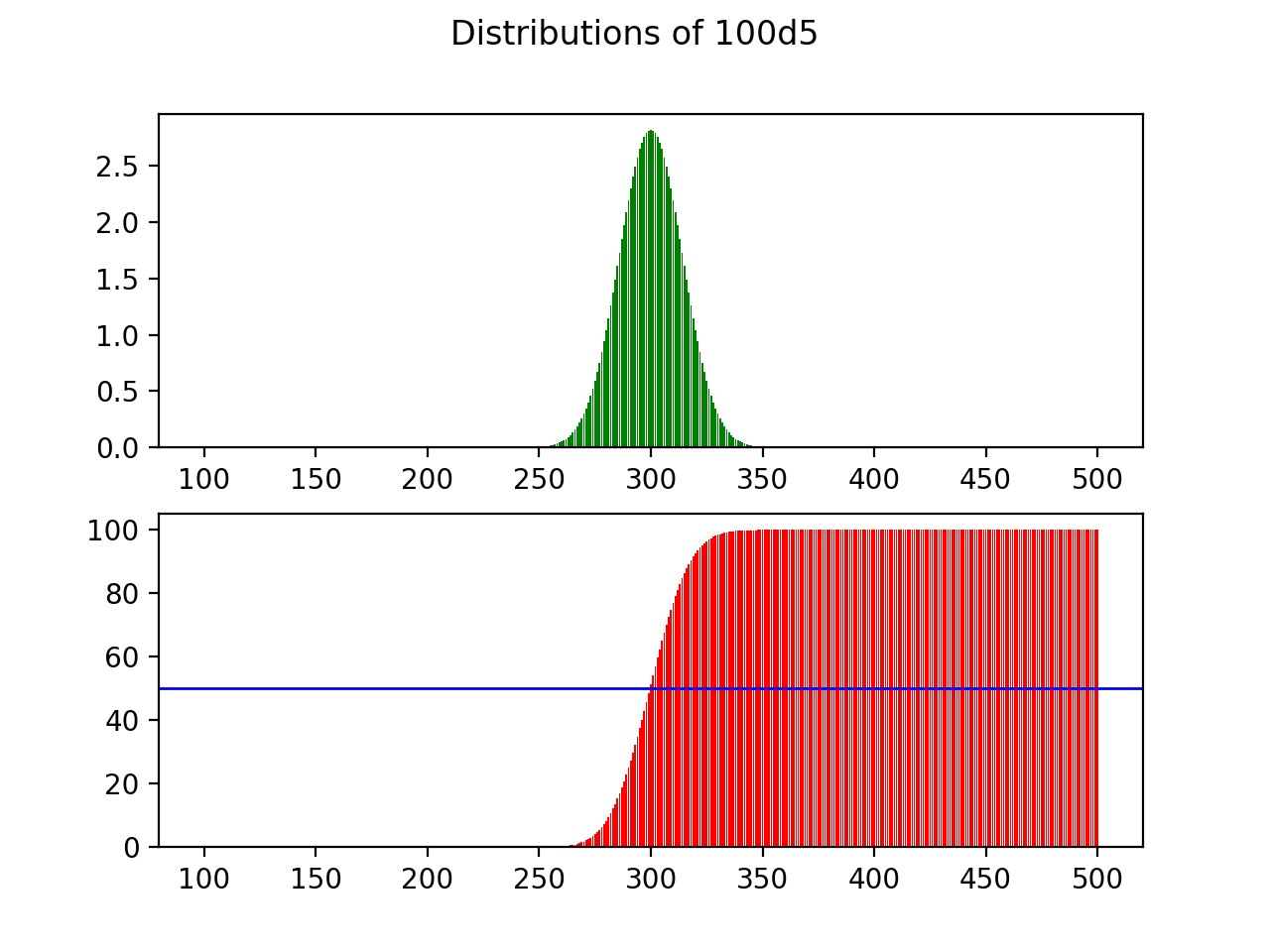
And it goes without saying, compared to the first build, the second method in unexaggeratedly, blindingly fast compared to the first one, completing the 14d6 distribution in less than a second. In fact, I went on to test this method for higher, more absurd dice counts, and it performs ‘reasonably’ even for 20d10 counts or 100d5 counts (and by ‘reasonably’, I mean it finishes within 10–20min, which is really quite impressive for the latter).

不用说，与第一个构建相比，第二个方法毫不夸张地比第一个方法快得令人眼花fast乱，在不到一秒钟的时间内完成了14d6分布。 实际上，我继续测试了此方法的更高，更荒谬的骰子计数，即使20d10计数或100d5计数也能“合理地”执行(并且“合理地”是指它在10至20分钟内完成，这的确是对于后者而言相当令人印象深刻)。

I haven’t really done any analysis as to the actual BigO notation for both of these methods, but they did strike me as very easy-to-recognize examples of just how important BigO efficiency is. Even in these problems, a totally plausible and useful real world example of generating the distribution of 14d6 had a runtime difference of between 1-second and 2-weeks depending on the algorithm we used, and the faster algorithm in this case allowed us to query sets that would have been completely unreasonable or impossible to run with the original build.

对于这两种方法的实际BigO表示法，我还没有进行任何分析，但是它们确实使我印象深刻，因为它很容易说明BigO效率的重要性。 即使在这些问题中，根据我们使用的算法，生成14d6分布的一个完全合理且有用的现实世界示例在运行时间上的差异介于1秒和2周之间，在这种情况下，更快的算法使我们可以查询设置将完全不合理或无法与原始版本一起运行。

I still haven’t been able to find a faster way to generate the distribution of die outcomes for an arbitrary number of arbitrarily sided die, despite my research. I’m strongly convinced that there is something out there to help, but I just haven’t known where to look. Regardless, this was a fun side-project to work on that I’ve been able to get a good deal of personal use out of, an exciting math problem to approach in my own time, and a solid reminder of the importance of runtime efficiency. Last but not least, this project has given me a cool, cathartic screen saver for a number-nerd like myself, and there’s always a way to push the algorithm to last as long as I want.

尽管我进行了研究，但我仍然无法找到一种更快的方法来生成任意数量任意面的模具的模具结果分布。 我坚信可以提供一些帮助，但是我不知道在哪里寻找。 无论如何，这是一个有趣的副项目，我可以充分利用它，在自己的时间内解决了一个令人兴奋的数学问题，并牢牢提醒了运行时效率的重要性。 最后但并非最不重要的一点是，该项目为像我这样的书呆子们提供了一个酷炫的导流屏保，并且总有一种方法可以使算法持续我想要的时间。

Below I’ve included another research article about a somewhat related, and somewhat unrelated dice problem analysis. I came across this article after I had done the work on this project, and if you liked this write-up, you will also certainly enjoy the one below. I hope you’ve enjoyed this project, and thanks for reading!

下面，我包括另一篇有关骰子问题分析的文章。 在完成该项目的工作后，我遇到了这篇文章，如果您喜欢这篇文章，那么您当然也会喜欢下面的文章。 希望您喜欢这个项目，并感谢您的阅读！