简介:计算机科学中的树结构和二叉树是数据组织的基础。树可以转换为二叉树,反之亦然。森林与广义表也可相互转换,通过递归或栈技术实现。理解这些转换与遍历方法对于掌握数据结构和算法设计至关重要。本话题涵盖了树与二叉树的转换细节,树的先序、中序遍历,以及森林的先根、后根遍历,并提供了相应的源代码实现。
1. 树与二叉树的定义和区别
在计算机科学中,树和二叉树是两种基本的数据结构,它们在信息的组织和检索中起着至关重要的作用。本章将对这两种结构进行详细介绍,并阐述它们之间的本质区别。
树的定义
树 是由节点(或称为顶点)与连接这些节点的边组成的图形结构。在树结构中,存在一个特殊的节点称为根节点,而每一个非根节点都有一个父节点,并且可以有多个子节点。节点之间没有环路,并且从根节点到任何节点都存在唯一的路径。
二叉树的定义
二叉树 是一种特殊的树结构,其每个节点最多有两个子节点,通常称为左子节点和右子节点。在二叉树中,节点的次序非常重要,因为这决定了树的形状和特性。二叉树在计算机科学中应用广泛,尤其是在构建表达式解析树和二叉搜索树时。
树与二叉树的区别
- 节点数量 :普通树的节点可以有任意数量的子节点,而二叉树每个节点最多有两个子节点。
- 子节点关系 :二叉树中节点的次序固定,左子节点和右子节点有明显的区别,但在普通树中这些关系并不明显。
- 结构特性 :二叉树的形状受其节点子节点数量的限制,因此对于具有n个节点的二叉树,其可能的形状数量是固定的。而普通树的形状则更为灵活。
通过理解这些基本概念和区别,我们可以进一步探讨树和二叉树在算法和数据结构中的应用,以及它们如何影响数据的组织和处理效率。接下来的章节将深入探讨树和二叉树的操作和应用。
2. 广义表与森林的转换方法
2.1 广义表的定义和特点
2.1.1 广义表的概念解析
在数据结构中,广义表是线性表的推广,可以将其视为列表的一种泛化形式。一个广义表可以是空表,也可以是由若干个表元素组成的序列。这些元素可以是单个数据元素,称为原子项,也可以是另一个广义表,称为子表。广义表的表示通常采用括号表示法,其结构类似于数学中的集合和函数的组合。
例如, (a, b, (c, d), e) 是一个广义表,其中 a , b , e 是原子项, (c, d) 是一个子表。
广义表与普通线性表的区别在于它的元素可以是原子也可以是子表,而普通线性表只能由原子组成。
2.1.2 广义表的线性结构与非线性结构
广义表可以拥有复杂的嵌套关系,因此它可以同时具有线性结构和非线性结构的特性。在分析广义表时,我们可以将其视为线性表的递归扩展:
-
线性结构: 如果我们忽略广义表中的子表,只考虑表尾的顺序,那么广义表就呈现出了线性结构的特性。例如,在广义表
(a, (b, c), d)中,如果我们只关注表尾的顺序,那么其线性结构为a -> b -> c -> d。 -
非线性结构: 广义表的非线性结构体现在其子表的存在上。这使得广义表不仅仅是一个简单的线性序列,而是一个可以多层次嵌套的复杂结构。在同一个广义表中,可以包含多个不同层次的子表,从而形成一种层次化的数据组织方式。
我们可以通过遍历广义表来展示其线性和非线性结构,尤其是其递归性质。在遍历过程中,我们需要同时处理原子项和子表,这在实际编程实现中需要特别注意。
2.2 森林的定义及其与树的关系
2.2.1 森林的构成和特性
森林是由多棵互不相交的树构成的集合,它是树的推广。在森林中,每棵树都保持其树的性质,即有且仅有一个根节点,并且树之间互不相连。森林的概念为树结构提供了一种更广阔的应用场景,特别是在需要处理多个树结构时。
森林的特性包括:
- 互不相交: 森林中的每棵树都是独立的,树与树之间没有任何连接点。
- 有序性: 森林可以看作是树的有序集合,树在森林中的排列顺序是有序的。
- 层次性: 每棵树都有明确的层次结构,从根节点到叶子节点形成清晰的路径。
2.2.2 森林与树的相互转换原理
森林与树之间的转换基于森林可以分解为多个独立树的事实。转换的主要原理是将森林中的树进行适当的组织以形成树或森林结构。这种转换通常通过以下方式实现:
- 将树转换为森林: 可以通过移除一棵树的根节点,将这棵树从森林中分离出来,其他树则形成新的森林。
- 将森林转换为树: 可以通过选取森林中的任意一棵树,并将其余树作为这棵树的子树,从而合并成一棵新的树。
在进行转换时,需要注意树结构的根节点是唯一的,并且在合并成树的过程中要保持原有的层次结构和父子关系不变。
这一转换过程不仅在理论上有趣,而且在实际应用中,如数据库设计和某些类型的数据结构处理中,也具有很大的价值。
下一章节将详细探讨森林转换为二叉树的算法,以及二叉树转换回森林的实现步骤。
3. 森林与二叉树的转换实现
在计算机科学中,森林和二叉树是两种不同的数据结构,它们在表示和处理信息方面各有所长。森林是一组不相交的树的集合,而二叉树是一种每个节点最多有两个子节点的树形结构。在某些情况下,将森林转换为二叉树,或者反之,可以简化问题,提高处理效率。本章将介绍森林与二叉树之间的转换方法,并探讨它们的实现细节。
3.1 森林转换为二叉树的算法
转换森林到二叉树是数据结构中一个重要的概念,尤其在编译原理中,对于表达式树的构造有直接的应用。这一过程的核心是建立一个二叉树,以保持原森林中所有树的结构和节点间的关系。
3.1.1 森林转换为二叉树的步骤
转换算法的基础思想是: 1. 从森林中取出第一棵树,将这棵树的根节点作为二叉树的根节点。 2. 然后,把这棵树的右子树设定为森林中下一颗树的根节点。 3. 重复以上步骤,直到森林中所有树都被转换成二叉树的右子树。
3.1.2 转换过程中节点关系的处理
为了在转换中保持节点间的关系,需要遵守以下规则: - 每棵树的第一个孩子成为转换后的二叉树节点的左孩子。 - 每棵树的下一棵树(即兄弟)成为转换后的二叉树节点的右孩子。
示例代码
下面是一个森林转换为二叉树的示例代码:
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def forest_to_btree(forest):
if not forest:
return None
root = forest[0] # 第一棵树的根节点作为二叉树的根
btree = root
btree.right = forest_to_btree(forest[1:]) # 将剩余的森林转换为右子树
current = btree
while current.left: # 将二叉树的左孩子设置为下一棵树的根节点
current = current.left
current.left = forest_to_btree([tree for tree in forest if tree != btree]) # 剩余森林中的第一棵树设为左孩子
return btree
# 假设有一个森林由多个TreeNode构成的列表
forest = [TreeNode(1), TreeNode(2), TreeNode(3)]
btree = forest_to_btree(forest)
在上述代码中,我们定义了一个 TreeNode 类,它代表二叉树中的一个节点。 forest_to_btree 函数接收一个森林的列表(每个树由一个根节点表示),并返回对应的二叉树的根节点。该函数递归地将森林转换为二叉树,并保持了森林中树间的关系。
3.2 二叉树转换回森林的实现
由于森林可以看作是多个根节点不相交的树,因此从二叉树转换回森林的原理也相对简单。每个二叉树的节点的左孩子和右孩子可以构成原森林中的一棵树。
3.2.1 二叉树转换为森林的原则
转换二叉树到森林的基本原则是: 1. 将二叉树的左孩子和右孩子分别作为一棵独立树的根节点。 2. 重复上述步骤直到所有的节点都被处理,且各自构成一棵独立的树。
3.2.2 转换后的森林结构分析
在转换过程中,每一步的节点都可能从二叉树的节点变为森林中一棵树的根节点。该过程遵循以下转换规则: - 二叉树节点的左孩子将作为转换后森林中的一棵树的根节点。 - 二叉树节点的右孩子将作为另一棵树的根节点,同时,该节点的右孩子又可能成为另一棵树的根节点,以此类推。
示例代码
以下是一个二叉树转换为森林的示例代码:
def btree_to_forest(btree):
if not btree:
return []
# 将左孩子和右孩子分别作为新森林的根节点
left_forest = btree_to_forest(btree.left) if btree.left else []
right_forest = btree_to_forest(btree.right) if btree.right else []
# 合并左子树森林和右子树森林,当前节点作为森林中的一棵树
return left_forest + right_forest + [btree]
# 假设有一个二叉树的根节点TreeNode实例btree
forest = btree_to_forest(btree)
在这段代码中, btree_to_forest 函数接收一个二叉树的根节点,并返回森林的列表,其中每个森林中的树由二叉树中的节点构成。函数通过递归地处理二叉树的左孩子和右孩子,最终形成森林结构。
4. 二叉树与遍历序列的相互转换
4.1 二叉树的遍历序列类型
4.1.1 先序遍历序列的构成
先序遍历(Pre-order Traversal)是一种深度优先的树遍历策略,其遍历顺序为根节点 -> 左子树 -> 右子树。在遍历过程中,首先访问根节点,然后递归地先序遍历左子树,接着递归地先序遍历右子树。先序遍历的顺序性使它在很多情况下能直接确定二叉树的结构,是理解其他遍历序列类型的基础。
4.1.2 中序遍历序列的构成
中序遍历(In-order Traversal)按照左子树 -> 根节点 -> 右子树的顺序访问节点。通过中序遍历可以获取一棵二叉搜索树(Binary Search Tree, BST)的所有节点值按照大小顺序排列的序列,这是其最主要的应用场景之一。中序遍历对于恢复树的结构也非常重要,尤其是当树的结构比较复杂时。
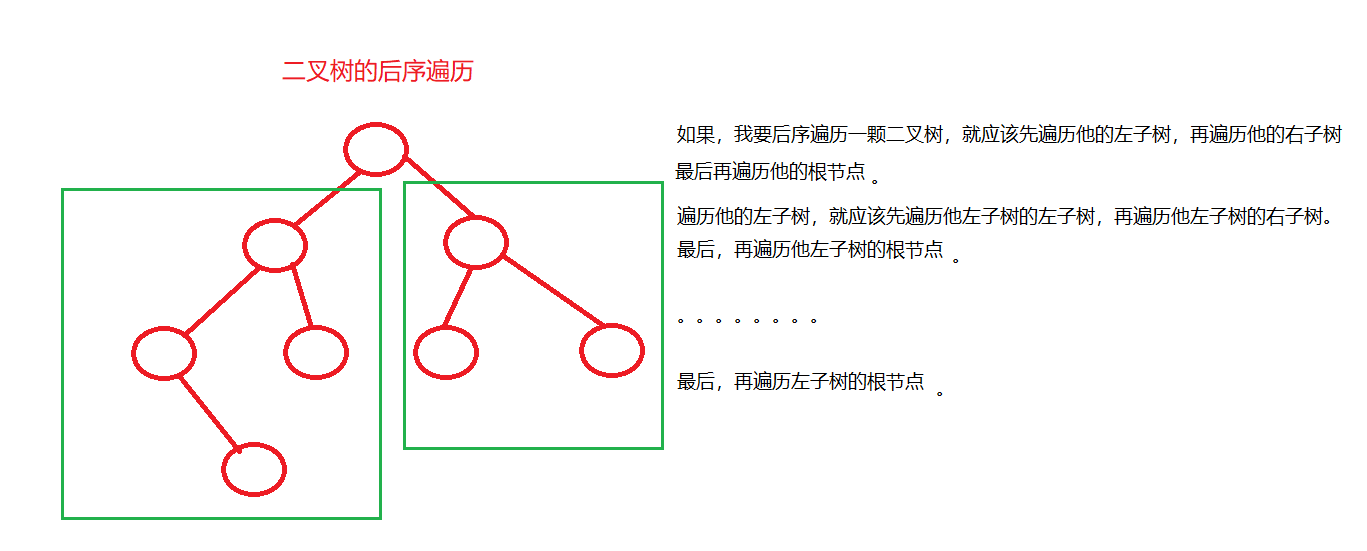
4.1.3 后序遍历序列的构成
后序遍历(Post-order Traversal)的顺序是左子树 -> 右子树 -> 根节点,是二叉树遍历的另一种深度优先策略。后序遍历序列能帮助我们了解二叉树的层次关系,特别适用于释放树的节点时,以确保先释放子节点再释放父节点,从而避免内存泄漏。
4.2 遍历序列重构二叉树的方法
4.2.1 已知先序和中序序列重构
要从先序遍历序列和中序遍历序列重构二叉树,我们需要明白两个遍历序列之间的关系。先序遍历的第一个值总是树的根节点,而在中序遍历序列中,根节点的值将序列分为左右两部分,对应左右子树。通过递归方式,我们可以将问题分解为更小的子问题,最终重构出原始二叉树。
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
def buildTree(preorder, inorder):
if not preorder or not inorder:
return None
# 先序遍历的第一个值是根节点
root_val = preorder[0]
root = TreeNode(root_val)
# 在中序遍历中找到根节点的位置
mid_idx = inorder.index(root_val)
# 递归地构建左子树和右子树
root.left = buildTree(preorder[1:mid_idx+1], inorder[:mid_idx])
root.right = buildTree(preorder[mid_idx+1:], inorder[mid_idx+1:])
return root
上述代码展示了如何递归地从给定的先序和中序遍历序列构建二叉树。每递归一次,我们就确定了树的一部分结构。
4.2.2 已知中序和后序序列重构
与先序和中序序列重构类似,中序和后序序列的结合也可以用来恢复二叉树的结构。后序遍历的最后一个值是树的根节点,在中序遍历序列中,根节点的位置同样将序列分为两部分,代表左右子树。通过递归方式,我们可以分别重构左右子树。
def buildTreeInPost(inorder, postorder):
if not inorder or not postorder:
return None
# 后序遍历的最后一个值是根节点
root_val = postorder[-1]
root = TreeNode(root_val)
# 在中序遍历中找到根节点的位置
mid_idx = inorder.index(root_val)
# 递归地构建左子树和右子树
root.left = buildTreeInPost(inorder[:mid_idx], postorder[:mid_idx])
root.right = buildTreeInPost(inorder[mid_idx+1:], postorder[mid_idx:-1])
return root
通过这种方式,我们可以根据中序和后序遍历序列恢复出原始的二叉树结构。重构二叉树的算法在数据恢复、二叉树操作等多个场景中有着广泛应用。
5. 先序遍历与中序遍历的具体步骤
5.1 先序遍历的算法实现
5.1.1 先序遍历的递归实现
先序遍历是树的遍历算法中的一种,它首先访问树的根节点,然后访问左子树,最后访问右子树。在递归实现中,算法会不断地将根节点的左子树和右子树分别进行先序遍历。
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
def preorderTraversal(root):
if root is None:
return []
return [root.val] + preorderTraversal(root.left) + preorderTraversal(root.right)
在上面的Python代码中, preorderTraversal 函数接受一个树节点作为输入,并返回一个列表,该列表中包含该树按先序遍历的节点值。首先检查当前节点是否为空,如果为空,则返回空列表。如果不是空,则将当前节点值添加到结果列表中,然后递归调用左子树,最后递归调用右子树。
5.1.2 先序遍历的非递归实现
非递归的先序遍历可以通过显式使用栈来实现。由于递归本质上就是使用了系统调用栈,因此转换为非递归形式就是用用户自定义的栈来模拟系统栈的行为。
def preorderTraversalIterative(root):
stack, result = [root], []
while stack:
node = stack.pop()
if node is not None:
result.append(node.val)
# 先右后左,保证左子树先被访问
stack.append(node.right)
stack.append(node.left)
return result
在这段代码中,我们创建了一个栈 stack 来存储将要访问的节点,并创建了 result 列表来存储遍历的结果。遍历过程中,我们从栈中弹出一个节点,访问它的值,并将其右子节点和左子节点压入栈中。右子节点先入栈是为了保证左子节点在之后能被首先访问,因为在栈结构中后进先出。
5.2 中序遍历的算法实现
5.2.1 中序遍历的递归实现
中序遍历先访问树的左子树,然后访问根节点,最后访问右子树。递归实现中,它不断地将左子树和右子树分别进行中序遍历,再访问根节点。
def inorderTraversal(root):
if root is None:
return []
return inorderTraversal(root.left) + [root.val] + inorderTraversal(root.right)
在这段代码中,我们递归地遍历了左子树,然后访问当前节点的值,接着递归遍历右子树。通过函数调用的返回顺序,我们可以保证节点值按左子节点、根节点、右子节点的顺序被添加到结果列表中。
5.2.2 中序遍历的非递归实现
非递归的中序遍历稍微复杂一些,因为它需要记录访问过的节点,以避免重复访问。这是通过一个额外的循环和栈来实现的。
def inorderTraversalIterative(root):
stack, result = [], []
current = root
while current is not None or stack:
# 遍历至左子节点最深
while current is not None:
stack.append(current)
current = current.left
# 访问节点
current = stack.pop()
result.append(current.val)
# 转向右子树
current = current.right
return result
在这段代码中,我们使用一个栈来保存遍历路径上的所有节点,然后使用一个循环来遍历树的左子树,直到最左边。当无法再向左移动时,我们开始出栈,访问节点值,并转向右子树。如此反复,直到栈为空且当前节点也为空。
通过上述递归和非递归两种方法,我们能够清晰地理解先序遍历和中序遍历的具体步骤和算法实现。接下来的第六章将探讨森林的遍历方法,包括先根遍历和后根遍历,以及递归和栈在树结构操作中的应用。
6. 森林先根遍历和后根遍历的描述
6.1 森林先根遍历的定义与算法
森林先根遍历,也称为先序遍历,是一种按照先访问根节点然后遍历子树的顺序来访问森林中所有节点的遍历方法。在遍历过程中,每个节点会按照"根节点-左子树-右子树"的顺序进行处理。
6.1.1 先根遍历的概念与步骤
先根遍历算法的步骤可以描述如下:
- 访问当前节点(即森林的第一个树的根节点)。
- 对当前节点的左子树递归执行先根遍历。
- 对当前节点的右子树递归执行先根遍历。
6.1.2 先根遍历的递归与非递归实现
递归实现先根遍历的伪代码如下:
FUNCTION PreorderTraversal(node)
IF node IS NOT NULL THEN
VISIT node
PreorderTraversal(node.left)
PreorderTraversal(node.right)
END IF
END FUNCTION
在非递归实现中,通常使用栈来模拟递归过程。以下是使用栈进行非递归先根遍历的伪代码:
FUNCTION PreorderTraversalIterative(root)
STACK stack = EMPTY_STACK
VISIT root
stack.push(root)
WHILE NOT stack.isEmpty() DO
node = stack.pop()
IF node.right IS NOT NULL THEN
stack.push(node.right)
END IF
IF node.left IS NOT NULL THEN
stack.push(node.left)
END IF
END WHILE
END FUNCTION
在森林中进行遍历时,可以通过遍历森林中的每棵树来实现先根遍历。对于森林中的每一棵树,按照树的先根遍历规则进行操作。
6.2 森林后根遍历的定义与算法
森林后根遍历,也称为后序遍历,是指按照先遍历子树然后访问根节点的顺序来访问森林中所有节点的遍历方法。在遍历过程中,每个节点会按照"左子树-右子树-根节点"的顺序进行处理。
6.2.1 后根遍历的概念与步骤
后根遍历算法的步骤可以描述如下:
- 对当前节点的左子树递归执行后根遍历。
- 对当前节点的右子树递归执行后根遍历。
- 访问当前节点(即森林的第一个树的根节点)。
6.2.2 后根遍历的递归与非递归实现
递归实现后根遍历的伪代码如下:
FUNCTION PostorderTraversal(node)
IF node IS NOT NULL THEN
PostorderTraversal(node.left)
PostorderTraversal(node.right)
VISIT node
END IF
END FUNCTION
非递归实现后根遍历通常较为复杂,因为需要记录节点的访问状态以及子树的访问顺序。一种可能的伪代码实现如下:
FUNCTION PostorderTraversalIterative(root)
STACK stack = EMPTY_STACK
STACK output = EMPTY_STACK
stack.push(root)
WHILE NOT stack.isEmpty() DO
node = stack.pop()
output.push(node)
IF node.left IS NOT NULL THEN
stack.push(node.left)
END IF
IF node.right IS NOT NULL THEN
stack.push(node.right)
END IF
END WHILE
WHILE NOT output.isEmpty() DO
node = output.pop()
VISIT node
END WHILE
END FUNCTION
在森林中进行后根遍历时,需要对森林中的每棵树分别进行后根遍历,并在适当的时候合并结果。
通过以上章节,我们了解到森林的遍历方法与树的遍历方法密切相关,但在实际应用中需要注意森林与树的结构差异,并适当调整遍历策略。递归和非递归实现提供了灵活的处理方式,适用于不同的情景和需求。
简介:计算机科学中的树结构和二叉树是数据组织的基础。树可以转换为二叉树,反之亦然。森林与广义表也可相互转换,通过递归或栈技术实现。理解这些转换与遍历方法对于掌握数据结构和算法设计至关重要。本话题涵盖了树与二叉树的转换细节,树的先序、中序遍历,以及森林的先根、后根遍历,并提供了相应的源代码实现。