C语言学习笔记：函数递归-斐波那契数列

C语言学习笔记：函数递归-斐波那契数列

什么是递归

在数学和计算机科学中，递归指由一种(或多种)简单的基本情况定义的一类对象或方法，并规定其他所有情况都能被还原为其基本情况。

递归就是在运行的过程中调用自己，递归关系就是实体自己和自己建立关系。

构成递归需具备的条件

1、子问题须与原始问题为同样的事，且更为简单；

2、不能无限制地调用本身，须有个出口，化简为非递归状况处理。

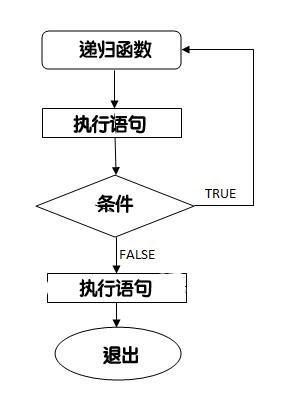
递归流程图

斐波纳契数列

这里有一道较为古典的问题：有一对兔子，从出生后第3个月起每个月都生一对兔子，小兔子长到第三个月后每个月又生一对兔子，假如兔子都不死，问每个月的兔子总数为多少？

这个问题我们可以通过找规律来解决：

第1个月的兔子对数: 1

第2个月的兔子对数: 1

第3个月的兔子对数: 2

第4个月的兔子对数: 3

第5个月的兔子对数: 5

第6个月的兔子对数: 8

第7个月的兔子对数: 13

……

通过列举这些月份的兔子数量，我们可以发现除了1、2月对数为1，后面每月的数量为前两月数量之和

放在数列里就成为{ a1=1，a2=1，an=a(n-1)+a(n-2)(n>=3,n∈N*1)}

而这个就是斐波那契数列，斐波纳契数列也是典型的递归案例

下面我们通过c语言编程来解决这个问题：

#include

int main(int argc,char const*argv[])

{

int n=0;

printf("输入月份：\n");

scanf("%d",&n);

printf("现在有%d对兔子\n",fbnq(n));

return 0;

}

int fbnq(int i)

{

if (i==1||i==2)

{

return 1;

}

else

{

return fbnq(i-1)+fbnq(i-2);

}

}

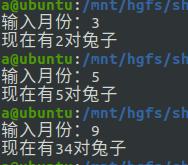
运行结果：

C语言学习笔记：函数递归-斐波那契数列相关教程