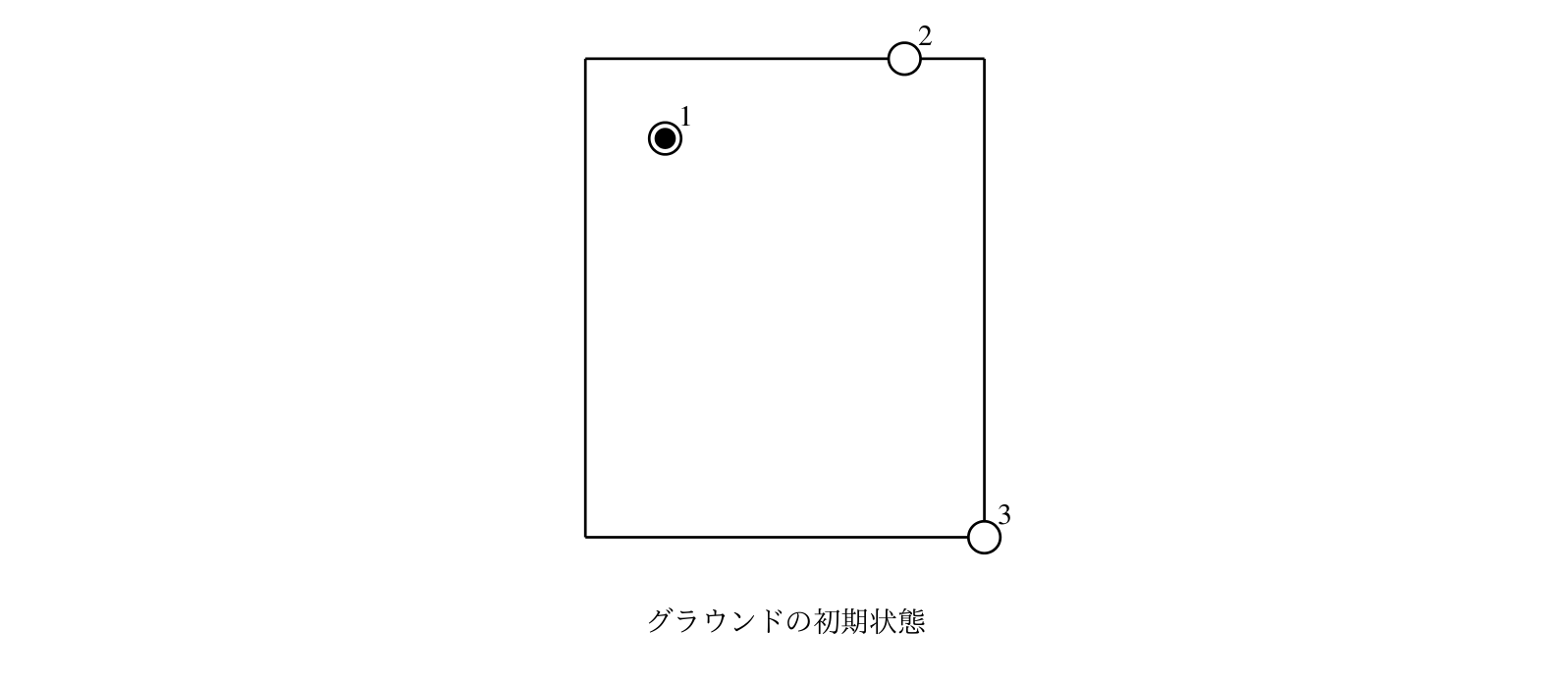
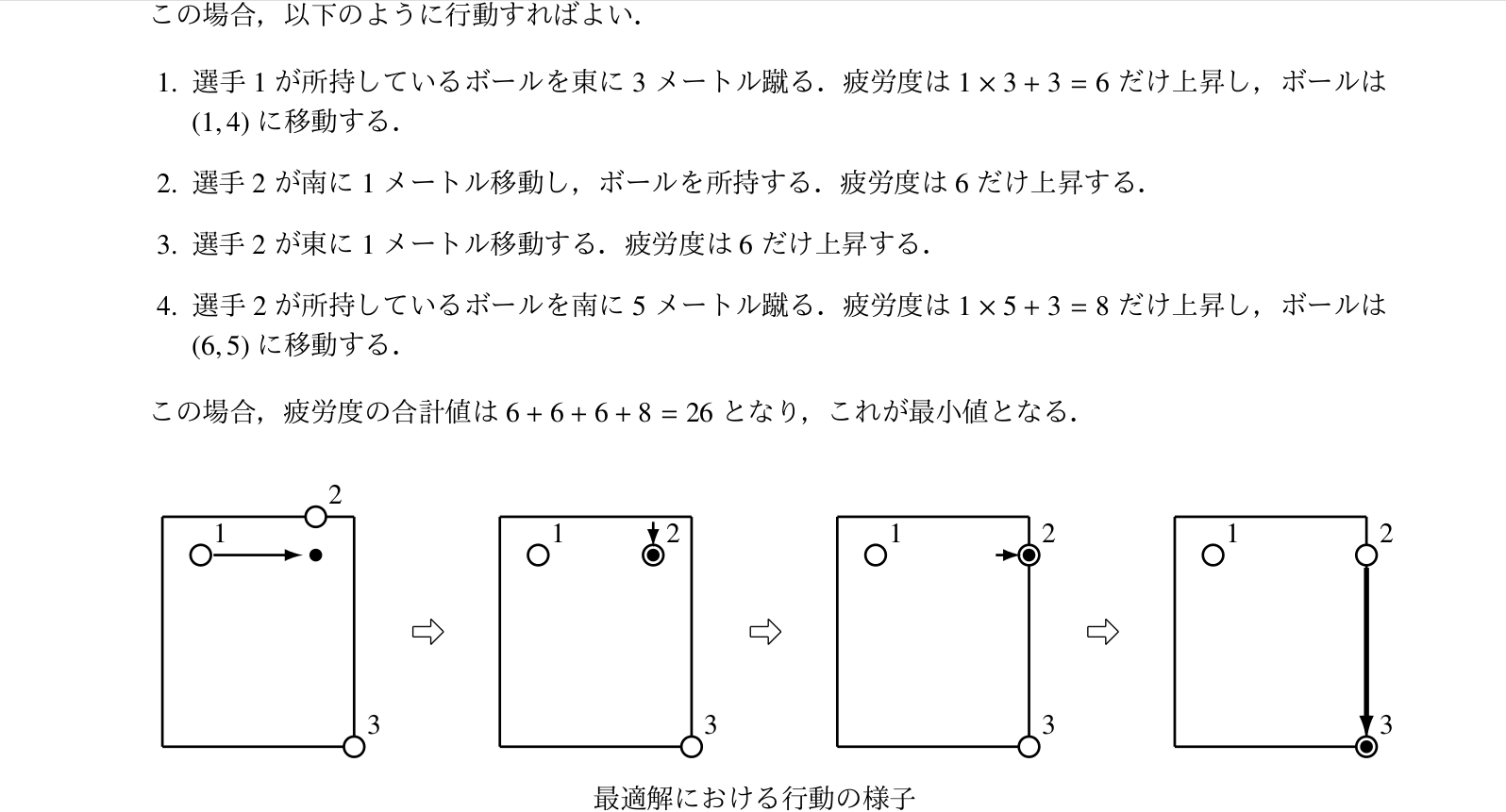
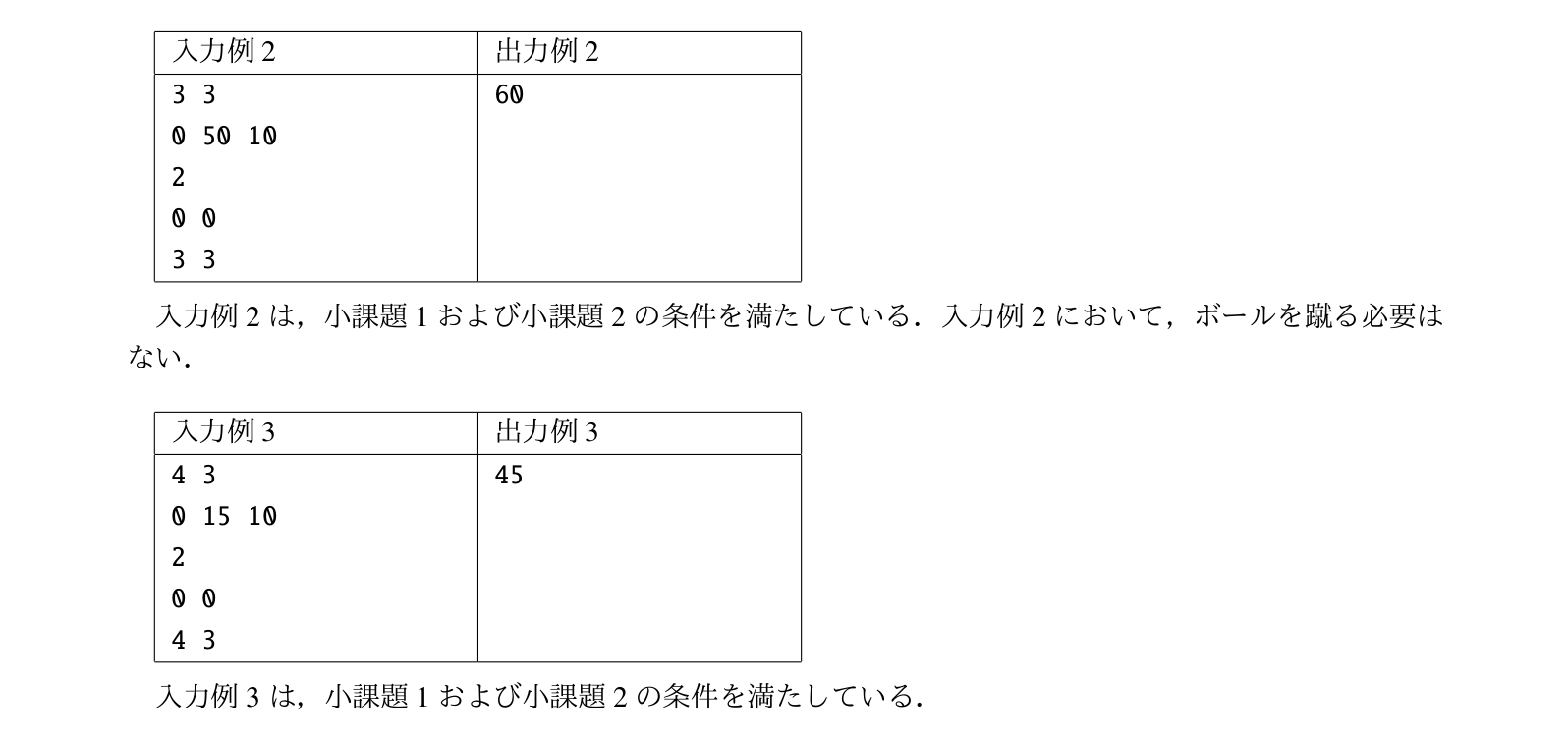
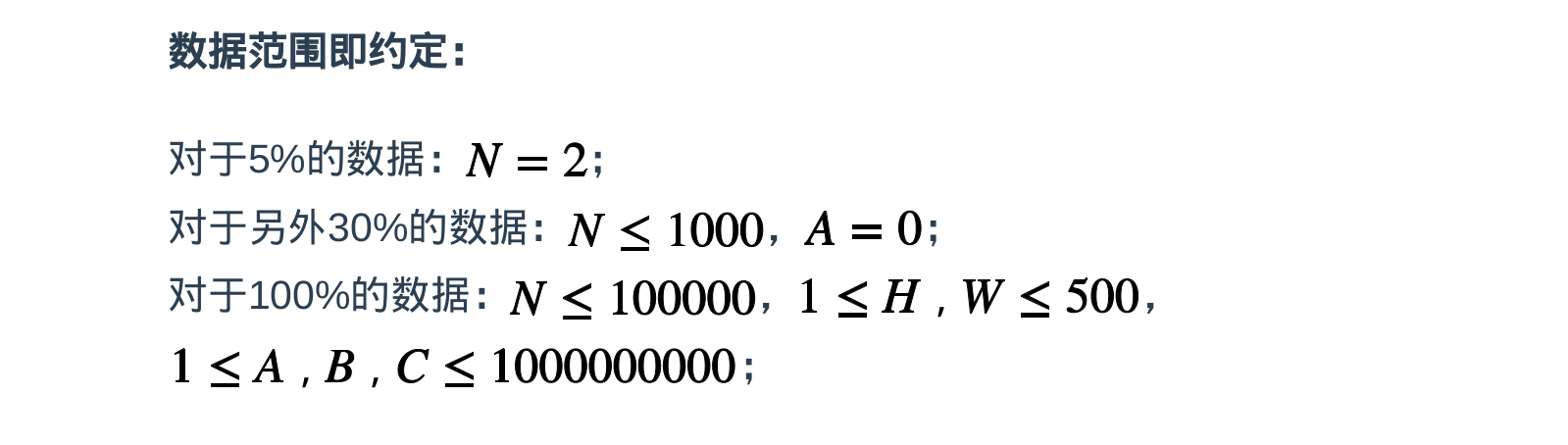原题题面看不懂的可以看下面的\(CJ\)版中文题面
$
$
\(CJ\)版:
$
$
这道题是\(JOI\)的\(T4\),放到联赛大概就是\(Day2,T3\)的难度
$
$
\(5\)分:
这一档分就是一个分类讨论,因为\(N=2\)
一共有\(3\)种情况可以出现最优解:
- \(1\)带球跑到\(2\),\(ans=C*(\left|h1-h2\right|+\left|w1-w2\right|)\)
- \(1\)带球纵向跑到与\(2\)齐平,踢球,\(ans=C*\left|h1-h2\right|+A*\left|w1-w2\right|+B\)
- \(1\)带球横向跑到与\(2\)齐平,踢球,\(ans=C*\left|w1-w2\right|+A*\left|h1-h2\right|+B\)
另外\(30\)分:
\(A=0\),也就是说踢球不取决于距离,踢球的花费完全取决于踢球的次数。
所以这里有两个结论,为了达到最优解,一个人不会踢球两次,一个人不会跑到其他地方去捡球来踢,这个结论画几个图就能够看出来,就不证明了。
那么整个过程就可以简化成:一个人带球跑,踢球,另一人接球,带球,再踢球。。。
这样就可以通过这个求出一个点到另一个点的最小花费,最后跑个最短路就可以求出来
\(100\)分:
这一问没有了\(A=0\)的条件,不过没有关系,上面的结论依然能用,一个人不会踢球两次。
而且这一问的\(N\)比较大,所以不可能直接对运动员进行处理。
然后我们就来想一下其他的做法。满数据的\(H\),\(W\)都比较小,我们可以把对运动员的处理换成直接对网格的处理。
设\(a[x][y]\)为步行到\((x,y)\)这个点的最小花费,这个可以\(bfs\)处理出来。
设\(ans[x][y][k]\),为在\((x,y)\)这个点时的几个状态的最小疲劳值,当\(0\le k\le3\)时,表示球从\(k\)方向滚到\((x,y)\)的最小疲劳值;当\(k=4\)时,表示运动员在\((x,y)\)持球的最小疲劳值。
那么具体怎么转移呢?
对于一个\(k=4\)的状态,它可以这样转移:
- 向各个方向走一格,\(ans[x'][y'][4]=ans[x][y][4]+C\);
- 向各个方向踢出球,\(ans[x][y][k']=ans[x][y][4]+B\);
对于一个\(k!=4\)的状态,它可以这样转移:
- 继续向前滚,\(ans[x'][y'][k]=ans[x][y][k]+A\);
- 一个运动员跑过来持球,\(ans[x][y][4]=ans[x][y][k]+C*a[x][y]\);
这个算法可以通过\(Dij\)来实现,最终的答案就是\(ans[hn][wn][4]\)。
时间复杂度:\(O(HW*logHW)\)
$
$
//made by Hero_of_Someone
#include<iostream>
#include<cstdio>
#include<cstdlib>
#define inf (1e17)
#define ll long long
#define il inline
#define RG register
using namespace std;
il int gi(){ RG int x=0,q=1; RG char ch=getchar(); while( ( ch<'0' || ch>'9' ) && ch!='-' ) ch=getchar();
if( ch=='-' ) q=-1,ch=getchar(); while(ch>='0' && ch<='9') x=x*10+ch-48,ch=getchar(); return q*x; }
il void File(){freopen("soccer.in","r",stdin); freopen("soccer.out","w",stdout);}
int h,w,n;
ll A,B,C;
ll a[540][540];
ll dis[50000010];
int H[1000010],W[1000010];
int qh[1000010],qw[1000010];
bool vis[540][540],v[50000010];
int dh[]={0,-1,0,1},dw[]={-1,0,1,0};
struct heap{
#define fa (x>>1)
#define ls (x<<1)
#define rs (x<<1|1)
int b[50000010],id[50000010],len;
il int top(){ return b[1]; }
il void push(RG int u){
if(!id[u]) id[u]=++len,b[len]=u; RG int x=id[u];
while(fa){
if(dis[b[x]]>=dis[b[fa]]) break;
swap(b[x],b[fa]),id[b[x]]=x,id[b[fa]]=fa,x=fa;
}
return;
}
il void pop(){
id[b[1]]=0,b[1]=b[len--]; if (len) id[b[1]]=1; RG int x=1,son;
while(ls<=len){
son=(rs<=len && dis[b[rs]]<dis[b[ls]]) ? rs : ls;
if(dis[b[x]]<=dis[b[son]]) break;
swap(b[x],b[son]),id[b[x]]=x,id[b[son]]=son,x=son;
}
return;
}
#undef fa
#undef ls
#undef rs
}que;
il void init(){
h=gi(),w=gi(),A=gi(),B=gi(),C=gi(),n=gi();
for(RG int i=0;i<n;i++){
H[i]=gi(),W[i]=gi();
if(!vis[H[i]][W[i]])
vis[H[i]][W[i]]=1;
else continue;
}
for(RG int i=0;i<=h;i++)
for(RG int j=0;j<=w;j++)
a[i][j]=inf;
RG int hd=0,tl=0;
for(RG int i=0;i<=h;i++)
for(RG int j=0;j<=w;j++)
if(vis[i][j]){ a[i][j]=0;
qh[tl]=i,qw[tl++]=j;
}
while(hd<tl){
RG int x=qh[hd],y=qw[hd];
for(RG int i=0;i<4;i++){
RG int xx=x+dh[i],yy=y+dw[i];
if(xx<0||xx>h||yy<0||yy>w) continue;
if(a[xx][yy]!=inf) continue;
a[xx][yy]=a[x][y]+1;
qh[tl]=xx,qw[tl++]=yy;
}
hd++;
}
}
il void work(){
for(RG int i=0;i<=h;i++)
for(RG int j=0;j<=w;j++)
for(RG int k=0;k<=4;k++)
dis[i*5000+j+k*10000000]=inf;
RG int t=H[0]*5000+W[0]+40000000;
dis[t]=0; que.push(t);
while(que.len){
RG int q=que.top();que.pop();
if(v[q]) continue; v[q]=1;
RG ll c=dis[q];
RG int dir=q/10000000;q%=10000000;
RG int x=q/5000,y=q%5000;
if(dir==4){
for(RG int i=0;i<4;i++){
RG int xx=x+dh[i],yy=y+dw[i];
if(xx<0||xx>h||yy<0||yy>w) continue;
RG int t=xx*5000+yy+40000000;
if(c+C<dis[t]){ dis[t]=c+C; que.push(t); }
}
for(RG int i=0;i<4;i++){
RG int t=x*5000+y+10000000*i;
if(c+B<dis[t]){ dis[t]=c+B; que.push(t); }
}
}
else{
RG int t=x*5000+y+40000000;
if(c+C*a[x][y]<dis[t]){
dis[t]=c+C*a[x][y]; que.push(t);
}
RG int xx=x+dh[dir],yy=y+dw[dir];
if(xx<0||xx>h||yy<0||yy>w) continue;
t=xx*5000+yy+10000000*dir;
if(c+A<dis[t]){ dis[t]=c+A; que.push(t); }
}
}
printf("%lld\n",dis[H[n-1]*5000+W[n-1]+40000000]);
}
int main(){ File(); init(); work(); return 0; }
(没事干写手写堆来玩玩)