模拟信号的数字处理,就是用离散时间系统来处理连续时间信号。我们在连续时间信号的离散时间处理以及离散时间信号的连续时间处理中已经学习过连续时间信号的离散时间处理,不过那只是单纯从理想的数学角度进行最简略的分析,这一篇文章中我们将从现实角度对这一过程进行分析,其中会讨论实现这一系统所需的各个模块。
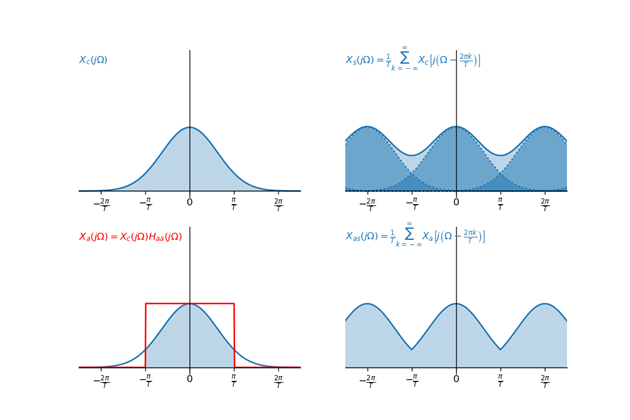
前面的笔记中的结构模型如下
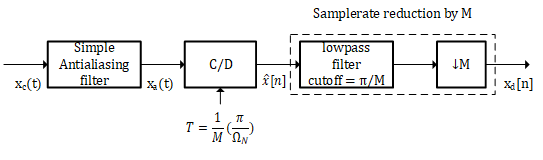
本文所讨论的较为现实的模型如下
其中包含
- 连续时间抗混叠滤波器
- 电平的采样与保持
- A/D转换器
- 离散时间系统
- D/A转换器
- 补偿重构滤波器
消除混叠的预滤波
理想抗混叠滤波器
在模拟信号转换成数字信号过程中,采样周期影响着每秒内数字信号的数量。采样周期越大(采样频率越小),则每秒所采集得到的数字信号的数量越少,这也意味着后续对这些数字信号处理所需的计算量越小。因此在对模拟信号进行采样的时候,总是希望在保证所需信号频率的前提下,使用尽量小的采样频率。以电话为例,尽管声音在4~20kHz内含有明显分量,不过电话的主要目的是传播人声,这只需要保证声音的频率在4kHz内就够了,因此电话在对声音进行采集的时候的采样率为8kHz。但是如果直接对原始声音进行采样,就会发生混叠现象,混叠引起的噪声被称为加性噪声(addictive noise)。为了避免这种噪声的产生,需要先对原始声音进行低通滤波,把大于4kHz的频率消去,这种滤波器被称为抗混叠滤波器(Antialiasing filter)。
理想情况下,抗混叠滤波器的频率响应为
$H_{aa}(j\Omega) = \left\{\begin{matrix}1, &|\Omega|<\Omega_c\leqslant \pi/T\\ 0, &|\Omega|\geqslant\Omega_c \end{matrix}\right.$
易实现的抗混叠滤波器
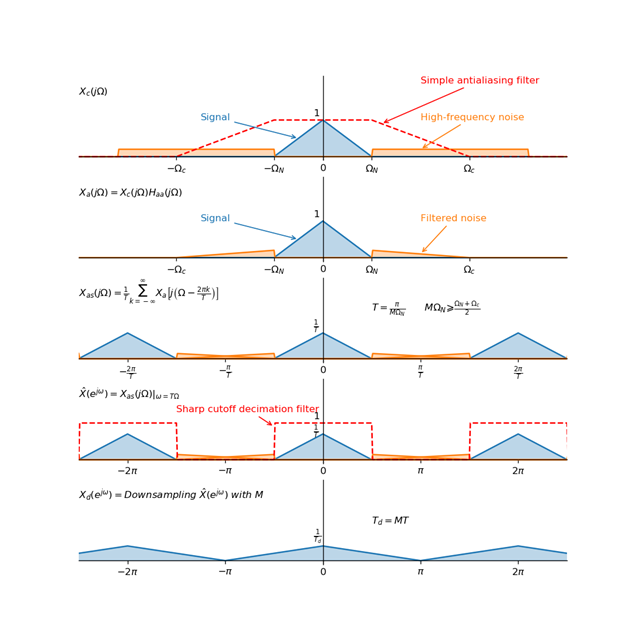
不过在模拟信号下的,设计一个在频域上具有直角(锐截止)的滤波器较为困难,并且需要较高的成本,因此下面将提出一个易于实现的抗混叠滤波器。该滤波器有如下结构:
- 在对模拟信号进行预滤波时,先用一个简单的不那么严格的低通滤波器进行滤波。频域上,该滤波器在$\Omega_N$一直到$M\Omega_c$处逐渐降为$0$。
- 在对预滤波后的信号进行采集的时候,仅要求$\Omega_N$内的频谱不被混叠,为了满足此条件,采样周期应满足$\frac{2\pi}{T}-\Omega_c\geqslant\Omega_N$,这里假设满足这一条件的采样周期为$T=\frac{\pi}{M\Omega_N}$,有$2M\Omega_N\geqslant\Omega_N+\Omega_c$。
- 等到了数字信号阶段,在对所采集得到的信号进行倍率为$M$的减采样,就能得到截至频率为$\Omega_N$的数字信号。
总结地说就是把较难实现的模拟信号低通滤波器进行简化,然后在数字信号进行处理时进行补救。这种实现方式在模拟信号的数字处理中有很广泛的应用。
模数(A/D)转换
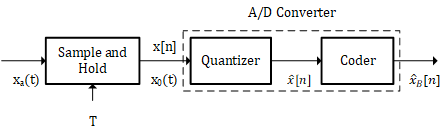
A/D转换目的是把连续时间信号转换为离散时间信号,具体表现为把代表连续时间信号的电压或者电流值转化为二进制码。A/D转换有如下结构
转换分为三个步骤
- 采样与保持。每间隔$T$对原始信号$x_a(t)$进行一次采样可得到一个电平,不过由于A/D转换不是瞬时就能完成的,因此有必要为A/D转换器提供一个稳定的电平,以此才能让A/D转换器输出一个准确的数值。
- 量化。A/D转换器得到电平后会对该数值进行量化,量化步长通常都是均匀的。
- 编码。得到量化电平之后,需要对该电平值进行二进制编码。
采样与保持
用数学式子来表示采样为
$x_s(t) = \displaystyle{\sum_{n=-\infty}^{\infty}x_a(nT)\delta(t-nT)}$
保持(这里又称零阶保持)的冲击响应为
$h_0(t) = \left\{\begin{matrix}1, & 0<t<T\\0, &else \end{matrix}\right.$
采样与保持系统也就是这两者的级联系统
$\begin{align*}
x_0(t) &= h_0(t)*\sum_{n=-\infty}^{\infty}x_a(nT)\delta(t-nT)\\
&= h_0(t)*\sum_{n=-\infty}^{\infty}x[n]\delta(t-nT)\\
&= \sum_{n=-\infty}^{\infty}x[n]h_0(t-nT)\\
\end{align*}$
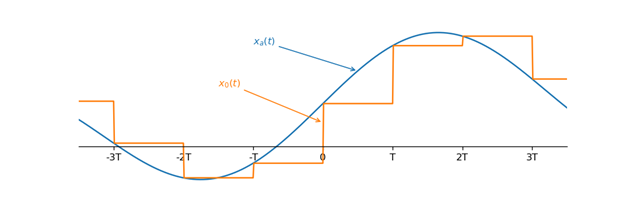
信号通过采用与保持系统后输出的将是一个阶梯波形
量化
量化就是把输入的样本$x[n]$映射到一个集合,该集合中的元素的数量是有限的,可表示为
$\hat{x}[n] = Q(x[n])$
$\hat{x}[n]$被称为量化样本,一般的量化器有如下表达式
$\hat{x}[n]= \left \lfloor\frac{ x[n]+\Delta/2 }{\Delta}\right \rfloor\Delta$
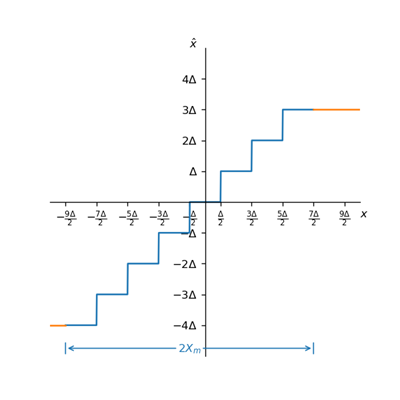
这个式子建立了从输入到输出的映射如下
x为输入,$\hat{x}$为输出,上图中有8个输出值可供映射($-4\Delta,-3\Delta,\cdot\cdot\cdot,3\Delta$)。除了输入以及输出外,量化器有两个重要参数:量化步长(又称量化阶)$\Delta$,全部量化区间的大小$2X_m$,量化会尽量把失真控制在$\frac{\Delta}{2}$以内,不过如果输入值超出量化区间的话,信号会由于截断而丢失过多的信息。
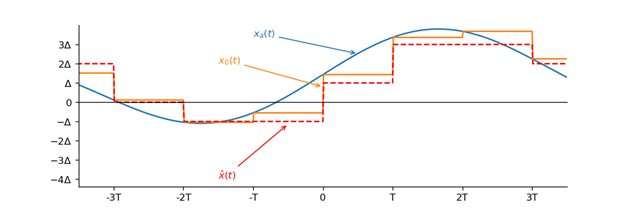
量化过后,波形会变为
二进制编码
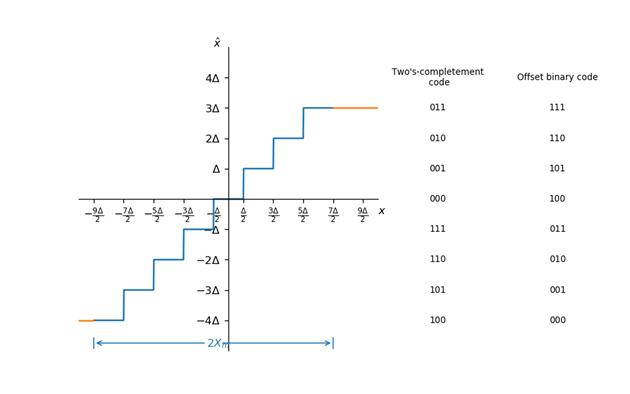
量化的结果是最终输出计算机能够处理的二进制数值,这里的二进制编码就是把上面的量化电平(量化后的样本)编码成二进制数值然后进行输出。以这一节所讨论的量化过程为例,一共有$-4\Delta$~$3\Delta$共8个量化电平,也就是说我们只用三个bit就能完成对该量化电平的编码。
上图有两种编码方法,每种编码方法都有8个码值,分别对应$-4\Delta$~$3\Delta$。
- 右边的编码方法的是Offset binary code,000代表在负数上最小的值,111代表正数最大的值。
- 左边的编码方法是Two's complement code,这种方法采用的是补码的方式进行编码,也就是计算机上对整数的编码方式,码字的最高位是符号位,剩下的是数值位。不过为了计算方便我们这里实际上会把除了符号为之外的数值当作分数,分母为$2^{B}$,其中$B+1$为码字的总长度。
| Two's complement code | Decimal | Fraction |
| 011 | 3 | 3/4 |
| 010 | 2 | 2/4 |
| 001 | 1 | 1/4 |
| 000 | 0 | 0 |
| 111 | -1 | -1/4 |
| 110 | -2 | -2/4 |
| 101 | -3 | -3/4 |
| 100 | -4 | -1 |
对于这种正负都有样本的信号,常用Two's complement code的编码方式,并且把编码的码值当作分数(如上述表格),这么一来,用$X_m$乘以该码值代表的分数就能得到量化样本。
$\hat{x}[n] = X_m\hat{x}_B[n]$
这里用$\hat{x}_B[n]$表示编码后输出的码字所代表的分数。
量化误差分析
量化误差的定义
量化前后的差值就是量化误差
$e[n] = \hat{x}[n] – x[n]$
继续对前面描述的例子展开讨论,例子当中会把$-\frac{\Delta}{2}<x[n]\leqslant \frac{\Delta}{2}$映射到$0$进行输出,把$\frac{\Delta}{2}<x[n]\leqslant\frac{3\Delta}{2}$映射到$\Delta$进行输出,以此类推。也就是说在上述例子中,如果能保证$-\frac{9\Delta}{2}<x[n]\leqslant \frac{7\Delta}{2}$,那么量化的误差能被控制在
$-\frac{\Delta}{2}<e[n]\leqslant \frac{\Delta}{2}$
如果输入的样本超出规定的范围,那么量化误差的幅度将超出$\frac{\Delta}{2}$,这些样本的状态被称为clipped,此时的量化器的状态被称为overloaded。
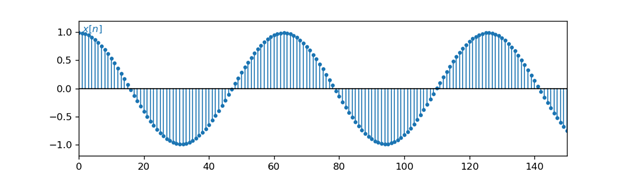
下面假设有一个余弦信号经过采样后的离散序列表示为$x[n] = 0.99cos(n/10)$:
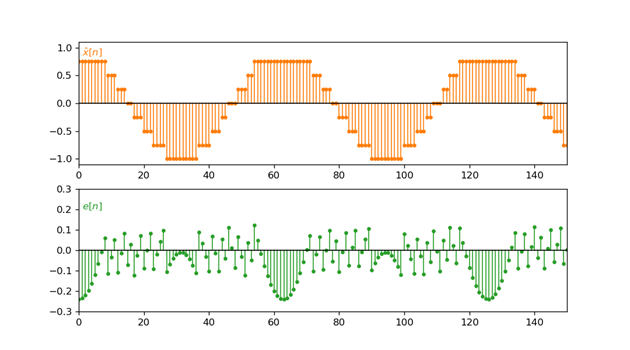
先采用三位的量化器($B+1=3$)对其进行量化:
可以发现该3位量化器的规定量化范围是$(-1.125, 0.875]$,而实际样本的范围是$[-0.99, 0.99]$,因此会出现overloaded的情况,见上图$e[n]$在$n=0,63,125$附近会出现较大的幅度。
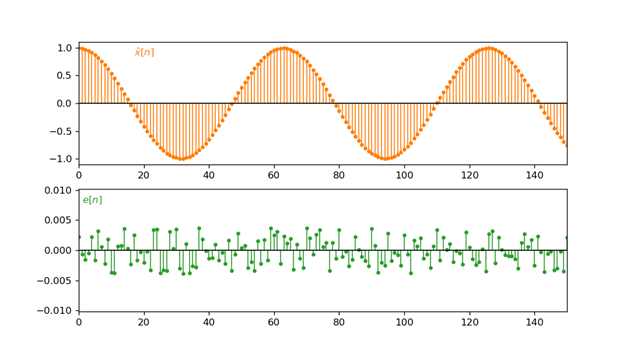
如果我们采用的是一个8位量化器$B+1=8$,那么有如下量化结果:
该8位量化器的规定量化范围为$(-\frac{257}{256}, \frac{255}{256}]$,涵盖了样本的范围$[-0.99, 0.99]$,因此不会出现overloaded现象。
量化误差的统计表示
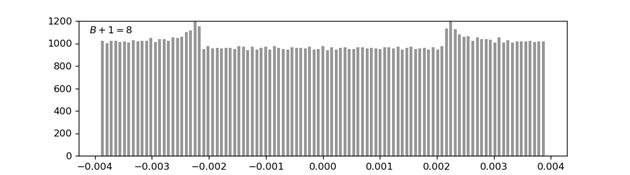
观察上面例子,发现在采用8位量化器的时候,量化误差有均匀概率随机分布的倾向。下面我们来对$n\in [0, 101000)$内的所有量化误差进行统计,以判断该量化误差是否为随机。我们这里把$(-\frac{\Delta}{2},\frac{\Delta}{2}]$分为101个区间,如果量化误差在$(-\frac{\Delta}{2},\frac{\Delta}{2}]$内呈现均匀概率的随机(Uniform Random),那么该101个区间中,每个区间的量化误差数目应该都在1000左右。
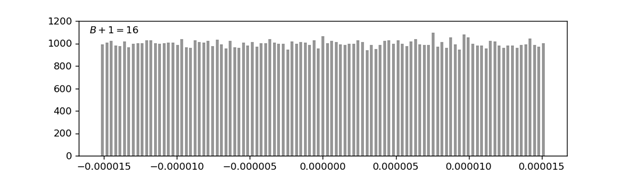
从上图可以看到虽然存在一定偏差,但是可以看到101个区间中统计得到的量化误差数目都在1000左右。下面是以16位量化器($B+1=16$)进行量化时的分布
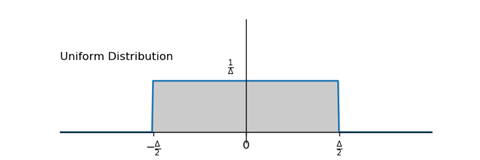
可以发现16位量化器比8位量化器的分布更加均匀,更加接近均匀概率密度的分布。实际上当信号是一个复杂信号的时候(语音或者音乐),通常就可以假设这些信号的量化噪声为这种均匀概率的随机过程。而量化位数越高,所得的分布曲线就会越接近理想的均匀概率分布(Uniform Distribution)曲线。
总结来说,量化误差的统计表示是基于如下假设:
- 误差序列$e[n]$是平稳随机过程的一个样本序列;
- 误差序列与序列$x[n]$不相关;
- 误差过程的随机变量之间是不相关的,也就是说,误差是一个白噪声过程;
- 误差过程的概率分布就是一个均匀概率分布。
信噪比
信噪比(SNR)主要用于判断噪声对原信号的污染程度,信噪比越大,则表明污染越小。
理论分析
前面的小节中已经得到了一个假设:$e[n]$是一个服从均匀概率分布的白噪声序列,均值为$\mu=0$,其方差为
$\displaystyle{\sigma_e^2=\int_{-\Delta/2}^{\Delta/2}(e-\mu)^2\frac{1}{\Delta}de= \left.\frac{1}{3\Delta}e^3\right|_{-\Delta/2}^{\Delta/2} = \frac{\Delta^2}{12}}$
对于一个$(B+1)$的量化器,其满幅度值为$X_m$,那么噪声方差或者说功率为
$\sigma_e^2 = \frac{2^{-2B}X_m^2}{12}$
信噪比的定义为信号的方差对噪声方差的比值,以db(分贝)表示:
$\color{red}{SNR_Q = 10log_{10}\left(\frac{\sigma_x^2}{\sigma_e^2}\right) = 10log_{10}\left(\frac{12\cdot 2^{2B}\sigma_x^2}{X_m^2}\right) = 6.02B+10.8-20log_{10}\left(\frac{X_m}{\sigma_x}\right)}$
从上面的式子可以看出,要提高信噪比,可以通过增加B,即增加量化器的量化位数来得到。每增加一位,就能增加约6db的信噪比。
此外,式子中还有需要特别考虑的一项
$-20log_{10}\left(\frac{X_m}{\sigma_x}\right)$
其中的$X_m$是量化范围的一半,通常在一个实际系统中是一个固定值,$\sigma_x$是信号的标准差,不过$\sigma_x$与原信号的峰值幅度$X_p$有正关系,这意味着$X_p$越大,则$\sigma_x$就会越大,这意味着,如果$\sigma_x$越大,则$X_p$有可能会超过$X_m$,使得$e[n]$不再服从均匀分布,那么上面信噪比的式子也就不再成立;如果$\sigma_x$越小,由于这一项是负项,因此这一项会随着$\frac{X_m}{\sigma_x}$的变大而变小,从而使得信噪比降低。
实际分析
我们这里研究实际信号的信噪比与$X_m/\sigma_x$以及$B$之间的关系。
实际的信噪比我们可以通过下面的式子进行计算得到
$\color{red}{SNR_Q = 10log_{10}\left(\frac{\sigma_x^2}{\sigma_e^2}\right) = 10log_{10}\left(\frac{\displaystyle{\frac{1}{N}\sum_{n=0}^{N-1}(x[n])^2}}{\displaystyle{\frac{1}{N}\sum_{n=0}^{N-1}(e[n])^2}}\right)}$
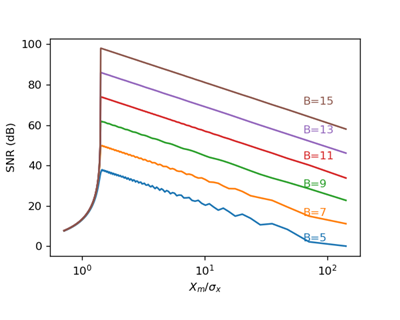
首先规定系统的$X_m = 1$,对于信号$x[n] = Acos(n/10)$,我们改变$A$就能改变$\sigma_x$,因此实现$X_m/\sigma_x$的改变。实际信号的信噪比与$X_m/\sigma_x$以及$B$的关系如下图:
- 观察发现当$X_m/\sigma_x$较大时,相邻的曲线之间相差约为$12dB$,回顾前面的理论$SNR_Q$公式,可以发现这是因为相邻的曲线相差的位数为$2$,$6.02B \approx 12$。
- 随着$X_m/\sigma_x$的变小,SNR也将上升到峰值。不过$X_m/\sigma_x$的变小意味着$\sigma_x$的增大,即信号的峰值$A$的增大,当$A$大到超出量化器规定的范围后,信号会被clipped,这会导致信噪比急速下降。
信噪比的实际应用
对于语音和音乐这样的模拟信号,幅度分布趋向于集中在零附近,并随着幅度的增加迅速跌落。在这些情况下,样本幅度超过标准差$\sigma_x$的3倍或者4倍的概率非常小。例如,如果信号幅度是一个高斯型分布,那么仅有0.064%的样本的幅度大于$4\sigma_x$。因此,为了避免信号峰值被clipped,可以在A/D转换器之前设置滤波器和放大器的增益,以使得$\sigma_x = X_m/4$,这就能保证被clipped的信号的概率小于0.064%。那么此时的信噪比为
$SNR_Q\approx 6B-1.25dB$
在对高质量的音乐进行录制或者重放时,如果采用的是这种系统,要获得90~96dB的信噪比,就要求有16位的量化。但是要记住,要达到这种性能需要知道输入信号的幅度的分布以及A/D转换器的规定范围,并对着两者进行精心匹配后才能实现。
数模(D/A)转换器
在连续时间信号的采样与重构中我们学习过,对离散序列重构为连续的信号,可以采用低通滤波器来实现。
$X_r(j\Omega) = X(e^{j\Omega T})H_r(j\Omega)$
式中,$X(e^{j\Omega T})=X(e^{j\omega})|_{\omega = \Omega T}$为样本序列的离散时间傅里叶变换,$X_r(j\Omega)$为重构的连续时间信号的傅里叶变换,理想重构滤波器为$H_r(j\Omega) = \left\{\begin{matrix}T, & |\Omega|<\pi/T\\0, &|\Omega|\geqslant\pi/T \end{matrix}\right.$。时域上,重构的信号与离散序列有如下关系
$x_r(t) = \displaystyle{ \sum_{n=-\infty}^{\infty}x[n]\frac{sin[\pi(t-nT)/T]}{\pi(t-nT)/T} }$
上述为一个理想D/C转换器。不过实际的系统通常把D/C转换分为两个部分:
- 数模(D/A)转换器
- 补偿重构滤波器
这一节主要讨论D/A转换器。
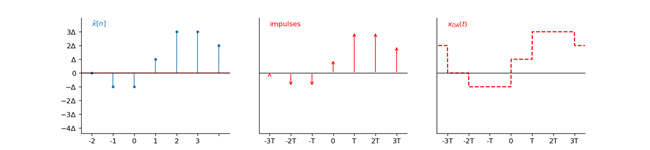
首先我们前面说过,这里的量化所得的二进制码字$\hat{x}_B[n]$是一个小数,用$X_m$乘以$\hat{x}_B[n]$即可得到实际的量化样本$\hat{x}[n]$。而D/A转换器就是A/D转换器的逆操作:以二进制码字序列$\hat{x}_B[n]$作为输入,产生一个由$\hat{x}[n]$保持$T$个单位时间的阶梯信号$x_{DA}(t)$。
这个过程中产生的信号变化如下
前面已经说过信号保持的脉冲响应如下:
$h_0(t) = \left\{\begin{matrix}1, & 0<t<T\\0, &else \end{matrix}\right.$
因此有
$\begin{align*}
x_{DA}(t) &= \sum_{n=-\infty}^{\infty}X_m\hat{x}_B[n]h_0(t-nT)\\
&= \sum_{n=-\infty}^{\infty}\hat{x}[n]h_0(t-nT)
\end{align*}$
补偿重构滤波器
通过D/A转换已经能得到一个连续时间的阶梯信号,在频域上有如下表示:
$\begin{align*}
X_{DA}(j\Omega) &= \mathcal{F}\left\{\sum_{n=-\infty}^{\infty}\hat{x}[n]h_0(t-nT)\right\}\\
&= \mathcal{F}\left\{\sum_{n=-\infty}^{\infty}\hat{x}[n]\delta(t-nT)*h_0(t)\right\}\\
&= \mathcal{F}\left\{\sum_{n=-\infty}^{\infty}\hat{x}[n]\delta(t-nT)\right\}\cdot\mathcal{F}\left\{h_0(t)\right\}\\
&= \left\{\sum_{n=-\infty}^{\infty}\hat{x}[n]\cdot\mathcal{F}\delta(t-nT) \right\}H_0(j\Omega)\\
&= \left\{\sum_{n=-\infty}^{\infty}\hat{x}[n]e^{-j\Omega Tn} \right\}H_0(j\Omega)\\
&= \hat{X}(e^{j\Omega T})H_0(j\Omega)
\end{align*}$
此时得到的已经是连续时间信号,但是阶梯信号并不是我们最终需要的重构信号,而所需要得到的重构信号为
$X_r(j\Omega) = \hat{X}(e^{j\Omega T})H_r(j\Omega)$
因此我们可以对$x_{DA}(t)$进行补偿,补偿滤波器在频域上的表示如下:
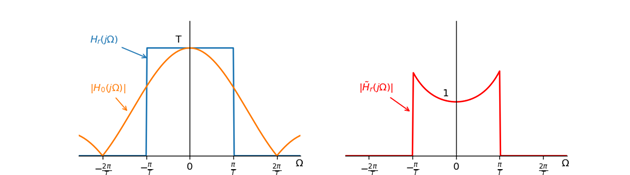
$\tilde{H}_r(j\Omega)=\frac{X_r(j\Omega)}{X_{DA}(j\Omega)}=\frac{H_r(j\Omega)}{H_0(j\Omega)}$
低通滤波器以及零阶保持滤波器的频率响应分别为:
$H_r(j\Omega)=\left\{\begin{matrix} T, &|\Omega|<\pi/T\\0, &|\Omega|\geqslant\pi/T \end{matrix}\right.\qquad H_0(j\Omega) = \frac{2sin(\Omega T/2)}{\Omega}e^{j\Omega T/2}$
因此补偿滤波器的频率响应为:
$\tilde{H}_r(j\Omega)=\left\{\begin{matrix} \frac{\pi T/2}{sin(\Omega T/2)}e^{j\Omega T/2}, &|\Omega|<\pi/T\\0, &|\Omega|\geqslant\pi/T \end{matrix}\right.$
系统的有效响应
本文主要讨论利用离散时间系统处理连续时间信号的模型,上述的各个小节分别对模型中的各个模块进行了较为详细的分析
对该模型进行逆推能得到下面的式子
$\begin{align*}Y_r(j\Omega)&=\tilde{H}_r(j\Omega)H_0(j\Omega)Y(e^{j\omega})\qquad lowpass\ filter\ H_r(j\Omega)=\tilde{H}_r(j\Omega)H_0(j\Omega)\ for\ restruction\\
&=\tilde{H}_r(j\Omega)H_0(j\Omega)H(e^{j\omega})\hat{X}(e^{j\omega})\qquad LTI\ system\ frequency\ response\ H(e^{j\omega})\\
&=\tilde{H}_r(j\Omega)H_0(j\Omega)H(e^{j\Omega T})\mathcal{F}\{x[n]+e[n]\}\qquad \hat{x}[n]=x[n]+e[n]\\
&=\tilde{H}_r(j\Omega)H_0(j\Omega)H(e^{j\Omega T})(X(e^{j\omega})+E(e^{j\omega}))\\
&=\tilde{H}_r(j\Omega)H_0(j\Omega)H(e^{j\Omega T})\left(\frac{1}{T}\sum_{k=-\infty}^{\infty}X_a\left[ j\left(\Omega-\frac{2\pi k}{T}\right)\right ]+E(e^{j\omega})\right)\\
&=\tilde{H}_r(j\Omega)H_0(j\Omega)H(e^{j\Omega T})\left(\frac{1}{T}X_a(j\Omega)+E(e^{j\omega})\right) \qquad \tilde{H}_r(j\Omega)\ will\ cutoff\ entries\ k\neq 0\\
&=\tilde{H}_r(j\Omega)H_0(j\Omega)H(e^{j\Omega T})\left(\frac{1}{T}H_{aa}(j\Omega)X_c(j\Omega)+E(e^{j\omega})\right)
\end{align*}$
其中$H_{aa}(j\Omega)$、$H_0(j\Omega)$、$\tilde{H}_r(j\Omega)$分别为抗混叠滤波器、D/A转换的零阶保持、补偿重构滤波器,$H(e^{j\Omega T})$是离散系统的频率响应。在忽略噪声的情况下,整个系统的有效响应为
$\color{red}{H_{eff}(j\Omega) = \frac{1}{T}\tilde{H}_r(j\Omega)H_0(j\Omega)H(e^{j\Omega T})H_{aa}(j\Omega)}$
从这个等效式子能够看出,理论上,系统中任意一个滤波器的不完善都能由其余的项来进行补足。