一、介绍

在正态分布中σ代表标准差,μ代表均值。x=μ即为图像的对称轴

3σ原则为

数值分布在（μ-σ,μ+σ)中的概率为0.6827

数值分布在（μ-2σ,μ+2σ)中的概率为0.9545

数值分布在（μ-3σ,μ+3σ)中的概率为0.9973

二、代码

数据主要是一串相似的值，自己提前判断能不能用σ就好了。用于处理小概率事件的剔除，当然，剔除是有代价的，需要样本数量足够大，具体要多大还得看你自己想提出成什么样子

主要地，先计算均值、标准差值，最后σ按自己设置的区间进行运算。当然这里也可以选择直接把坏值m(t)剔除，置零操作。

  对于代码内提到的'matlab.mat'，举个例子，就不方便把数据拿出来，拿出来好像也没什么用。如下：

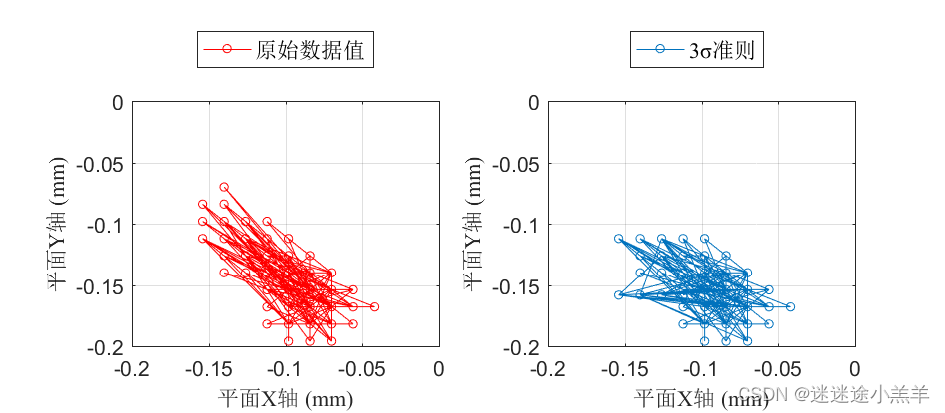
        我在监视一辆小车保持于原点，但实际上监视得到的点并不准确（会有零漂、温漂等问题导致波动）；我已知在实际运动中，小车X轴的运动轨迹是准确的，而Y轴有问题，为了粗略计算我只能设法省略掉那些漂移的点。所以，（jiguangx，jiguangy）这是图一的坐标各点；然后单独对Y轴矢量进行概率省略，省略掉的Y轴用平均值替代，就能得到（jiguangx，n）如图二。
当然也可以适用于X轴或是平面（x，y）坐标点，不过如果是对二维坐标点进行概率省略，可能更适合对位移平方进行省略？具体情况具体分析吧。

clc;
clear;
load('matlab.mat');
figure(1);
set(gcf,'units','centimeters','Position',[5,5,16,7], 'color','w');

%第一幅图，原始数据
subplot(1,2,1);
plot(jiguangx,jiguuangy,'ro-','MarkerSize',4);
axis([-0.2 0,-0.2,0]);
lg1=legend( '\fontname{宋体}原始数据值','Location','NorthOutside','Orientation','horizontal');
set(lg1,'FontSize',10.5);
grid on;
box on;
xlabel('\fontname{宋体}平面\fontname{Times New Roman}X\fontname{宋体}轴\fontname{Times New Roman} (mm)','FontSize',10.5);
ylabel('\fontname{宋体}平面\fontname{Times New Roman}Y\fontname{宋体}轴\fontname{Times New Roman} (mm)','FontSize',10.5);


%装载数据开始剔除小概率事件
%数值分布在（μ-3σ,μ+3σ)
a=jiguuangy;
aa=mean(a); %计算平均值
sig=std(a); %计算标准偏差
m=zeros(1,length(a));%所有数据列为一个矩阵
i=1;
for t=1:length(a)
	m(t)=abs(a(t)-aa);
	if m(t)>3*sig
  		n(t)=aa;%将异常值替换成了均值
  		i=i+1;
	else
  		n(t)=a(t);
  	end
end

%第二幅图，剔除后的数据
subplot(1,2,2);
plot(jiguangx,n,'o-','MarkerSize',4);
axis([-0.2 0,-0.2,0]);
lg1=legend( '\fontname{Times New Roman}3σ\fontname{宋体}准则','Location','NorthOutside','Orientation','horizontal');
set(lg1,'FontSize',10.5);
grid on;
box on;
xlabel('\fontname{宋体}平面\fontname{Times New Roman}X\fontname{宋体}轴\fontname{Times New Roman} (mm)','FontSize',10.5);
ylabel('\fontname{宋体}平面\fontname{Times New Roman}Y\fontname{宋体}轴\fontname{Times New Roman} (mm)','FontSize',10.5);

三、运行效果

 基本实现功能