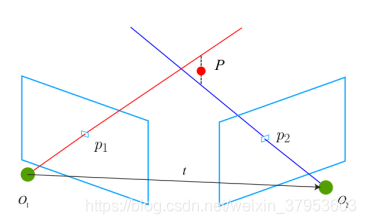
问题描述：
考虑某个路标点 $y$（上图的P）被若干关键帧 $\mathrm{k}=1,2\dots \mathrm{n}$（上图的O）看到。
其中，$y\in {\mathbb{R}}^4$取齐次坐标，即$y=[x,y,z,1{]}^T$。每次观测为$x_k={\left[u_k,v_k,1\right]}^T$，取相机归一化平面坐标（这样可以忽略内参）。
记世界系到相机系的投影矩阵为$P_k=\left[R_k,t_k\right]\in {\mathbb{R}}^{3\times 4}$。
投影关系：
$$\forall \mathrm{k},{\lambda }_{\mathrm{k}}{\mathrm{x}}_{\mathrm{k}}={\mathrm{P}}_{\mathrm{k}}\mathrm{y}$$
其中观测点深度值${\lambda }_{\mathrm{k}}$未知
将投影关系写开：
$$\{\begin{array}{l}{\lambda }_k{u}_k=p_{k,1}y=\left[R_{k,1}\mid t_{k,1}\right][x,y,z,1{]}^T\\ {\lambda }_k{v}_k=p_{k,2}y=\left[R_{k,2}\mid t_{k,2}\right][x,y,z,1{]}^T\\ {\lambda }_k=p_{k,3}y=\left[R_{k,3}\mid t_{k,3}\right][x,y,z,1{]}^T\end{array}$$
其中为的第一行，容易发现第三式可以带入上两个式子，将深度值消元。
$$\{\begin{array}{l}{p}_{k,3}y{u}_k=p_{k,1}y\\ p_{k,3}y{v}_k=p_{k,2}y\end{array}$$
化简得:
$$\{\begin{array}{l}\left(p_{k,3}{u}_k-p_{k,1}\right)y=0\\ \left(p_{k,3}{v}_k-p_{k,2}\right)y=0\end{array}$$
由于我们现在要求解$y=[x,y,z,1{]}^T$，有三个未知数，上面两个方程是不够的，至少得多一个观测(当然多几个观测结果是一样的)：
$$\{\begin{array}{l}\left(p_{1,3}{u}_k-p_{1,1}\right)y=0\\ \left(p_{1,3}{v}_k-p_{1,2}\right)y=0\\ \left(p_{2,3}{u}_k-p_{2,1}\right)y=0\\ \left(p_{2,3}{v}_k-p_{2,2}\right)y=0\end{array}$$
整合得:
$$\left[\begin{array}{l}{p}_{1,3}{u}_k-p_{1,1}\\ p_{1,3}{v}_k-p_{1,2}\\ p_{2,3}{u}_k-p_{2,1}\\ p_{2,3}{v}_k-p_{2,2}\end{array}\right][y]=0\Rightarrow Dy=0$$
y为D零空间的一个非零元素。本来就是三个未知数，这时来了四个方程，系数矩阵必不满秩（在丁点噪声都没有的情况下,也就是上图红蓝线相交）。
若对D的SVD分解，$\mathrm{D}=\mathrm{U}\Sigma {\mathrm{V}}^{\mathrm{T}}$，$\Sigma$为矩阵D特征值由大到小的组成的对角矩阵。挪一下位置，实际上是$\mathrm{D}\mathrm{V}=\mathrm{U}\Sigma$，如果将上述结果$\mathrm{D}\mathrm{y}=0$，对应地放入SVD分解的式子中。
$$\mathrm{D}\left[{\mathrm{v}}_1\dots \mathrm{y}\right]=\mathrm{U}\left[\begin{array}{ccc}{\sigma }_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \dots & 0\end{array}\right]$$
显而易见，我们求解y只要对D做SVD分解，再取V矩阵的最后一维即可。But……实际操作上，我们会对做奇异值分解（这就成了特征值分解了阿），同样取V的最后一维。
$$D^{T}D={\left(U\Sigma V^T\right)}^{T}U\Sigma V^T=V{\Sigma }^T{U}^{T}U\Sigma V^T=V\left({\Sigma }^T\Sigma \right)V^T$$

一开始，我也很迷，为啥要算，分明算D就行了。认识太薄弱了，然后去b站学习了，MIT还有3b1b。
视频参考（MIT），这就明明白白：SVD分解
发现老师是这么讲的，我们用手算的过程也是这么算的，关键还是我代码这样运行是比较快的，哈哈哈。

另外，由于噪声的存在，D矩阵经常是满秩，这样我们原来假设零空间里的y就不存在了。因此在解SVD的时候，我们还要判断奇异值的${\sigma }_3>>{\sigma }_4$是否成立。若不成立，这意味着则三角测量是失败的，我们则要增加观测。
为什么要增加观测呢？我自己理解哈，噪声是服从零均值的高斯分布的（这是不是又太理想了，哈哈哈），只要你采样多了，这个“零”就会显现了，反之少的时候，一下子就把你带偏了；另外“多次实验得出普遍真理”嘛～

碎碎念：投影矩阵实际上就是相机的位姿变换。我们定第一帧坐标与世界坐标重合，根据上回说到的极对约束，我们根据匹配点，求解得第一帧与第二帧相机运动关系。同时这些匹配点，根据定义的第一帧与世界坐标重合，确定了点的世界坐标。在通过PNP等即可生成往后连续的位姿。这样说来，投影矩阵P所有是已知的。（我们用路标点求解位姿，又返回来用位姿去优化路标点的“深度”，形成一个“闭环”）

文为小记，但若有不当之处，还望赐教！
参考及盗图：深蓝学院vio，MIT线代，3b1b，十四讲