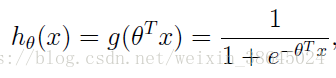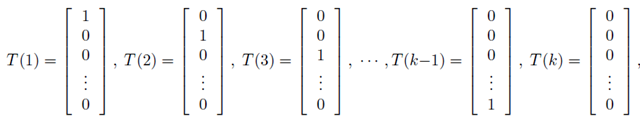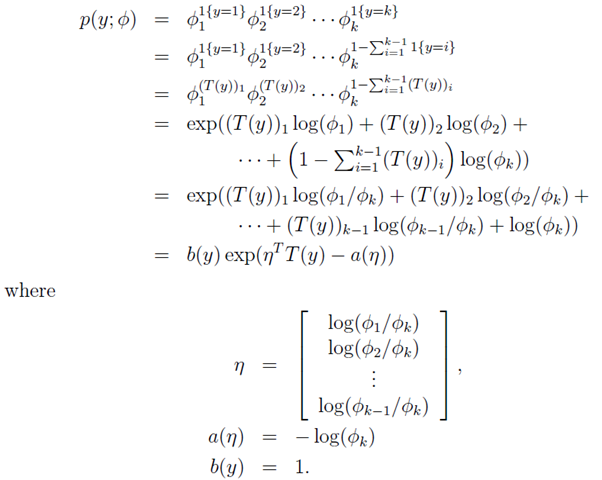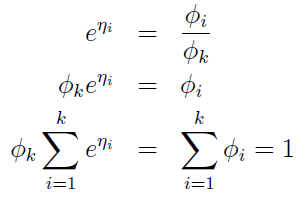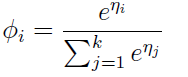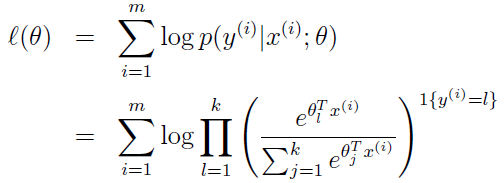1 回归与分类
线性回归的损失函数选择时候,基于误差分布的客观假定,通过最大似然的计算法则得出了损失函数。其实在对一个样本分布进行建模和预测的时候,更本质上来讲是对一个样本概率分布的预测,其概率分布依赖于训练样本和规则(算法)。因此在数学意义上来讲,机器学习的最优化选择是样本概率分布的最大点的预测。
回归模型和分类模型可以通过sigmoid函数和softmax函数建立联系。
注意:回归预测模型是通过离散的数据点建立连续模型,因此线性回归等预测模型收到噪声点影响比较大。
2 logical分类器和softmax分类器
logistic分类器是以Bernoulli(伯努利)分布为模型建模的,它可以用来分两种类别;而softmax分类器以多项式分布(Multinomial Distribution)为模型建模的,它可以分多种互斥的类别。
Logistic 分类器
要解决什么样的问题呢??假设有一训练样本集合X = {x1, x2, x3, ……},其中样本 xi 由一系列的属性表示即,xi = (a1, a2, a3,……),并且对于样本集合X中的样本要么属于类别0, 要么属于类别1.
现在呢,我们有一个测试样本x, 我们根椐上面的知识来推断: 样本x 属于类别0 还是类别1呢??
下面来解决这个问题哦:
1,首先引入参数θ=(θ1,θ2,θ3,……),对于样本中的属性进行加权,得到:θTx
2,引入logistic函数(sigmoid函数):g(z) = 1 / (1 + e-z), 该函数常作为神经网络里的激活函数的;构建这么一个式子(待会就会明白它的含义):
3. 现在我们有: P(y = 1 | x; θ) = hθ(x) , 与 P(y = 0 | x; θ) = 1 - hθ(x), 那么呢,我们把它俩联合起来, 得到:P(y | x; θ) = {hθ(x)}y{(1-hθ(x)}1-y.
4. P(y | x; θ) 含义是在给定样本 x 与参数 θ 时,标签为y 的概率。现在我们假设每一个训练样本是独立的,我们写出它们联合概率密度:
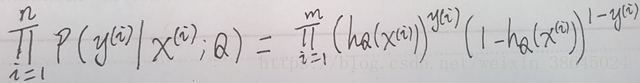
5.最大化似然函数,求出合适的参数θ。
softmax分类器
假设有一训练样本集合X = {x1, x2, x3, ……},其中样本 xi 由一系列的属性表示即,xi = (a1, a2, a3,……),并且对于样本集合X中的样本属于类别C = {c1, c2, c3, ……}中的一种。
下面正式推一下softmax回归 (可以用它用分类器的哦)
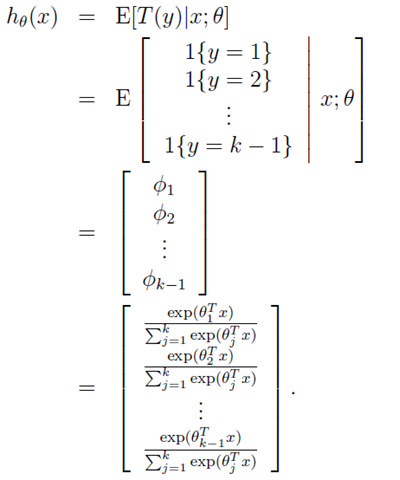
上面已经说了,对于给定的测试样本 x , 它的输出 有k种可能 (即可以分为k类),我们分别φ1,φ2,φ3,φ4,……,然后呢,我们定义T(y)如下:
并且定义一个运算 I{真} = 1, I{假} = 0; 所以呢,有:
1,上面的(T(y))i = I{y = i} ,其中(T(y))i 表示T(y)的第i 个元素);
2,E[(T(y))i] = P(y = i) = φi.
下面为推导过程:假设以已经φ的情况,把 p(y; φ)写出指数分布族的形式,如下 所示:
注意上面的η是K-1 维的哦,我们现在规定ηk = log(φk/φk) = 0。所以呢, ηi = log(φi / φk),其中i =1,2,……,k)
然后呢,
所以呢,推出:
上面我们假设的φi 已经知道了,其实我们不知道哦,现在我们就推出了怎么去求φi 了。上面的式子表示了怎么由ηi去求θi,这就是softmax函数。对于上式的 ηi = θiT x.(应用上面的第三个假设)。 还因为ηk =0,所以呢,我们又规定了θk = 0。(所以,这里一定注意,θk还是未知数哈,待会用得到这一点)。
其实到这里基本已经完了,因为我们所关心的φi 已经知道怎么去求了。
接下来呢,我们来预测T(y)的值哈(看假设的广义线性模型中的第二点哦)
到这里就剩下最后一步了,求拟合参数 θ1,θ2,……,θk-1。 可能会问什么没有θk呢,因为我们上面规定了θk=0. 追根到底是因为:φk =1-(φ1+φ2+ ……+φk-1).
如何求呢,我们写出它的似然函数,然后就可以转变为:用梯主下降或牛顿法等求最值的问题了。它的拟然函数为:
现在呢,我们把参数已经求出来了,可以解决我们的问题了,即给定了一个测试样本,我们估计它属于哪一类。方法是我们分别求出对应的φi, 哪个最大,它就属于哪一类了。
3 代码实例
一个基于Python实现的关于垃圾邮件分类的实例。代码