蓝桥杯 第几个幸运数

2018年蓝桥杯做出这个填空题，没想到2022年我竟然还能看到这道题，四年了

到x星球旅行的游客都被发给一个整数，作为游客编号。
x星的国王有个怪癖，他只喜欢数字3,5和7。
国王规定，游客的编号如果只含有因子：3,5,7,就可以获得一份奖品。

我们来看前10个幸运数字是：
3 5 7 9 15 21 25 27 35 45
因而第11个幸运数字是：49

小明领到了一个幸运数字 59084709587505，他去领奖的时候，人家要求他准确地说出这是第几个幸运数字，否则领不到奖品。

请你帮小明计算一下，59084709587505是第几个幸运数字。

需要提交的是一个整数，请不要填写任何多余内容。

思路 ：构造数，用当前构造出来的数依次$\ast 3,\ast 5,\ast 7$,如果构造出来的数比幸运数字大就舍弃，轮到幸运数去$\ast 3,\ast 5，\ast 7$ 时，set的长度即为幸运数字的序号

方案1

#include<bits/stdc++.h>

using namespace std;
typedef long long LL;
const LL Max = 59084709587505;
int a[3] = {3,5,7};

void Find(LL Max)
{
    set<LL> se;
    LL t  = 1;
    while(1)
    {
        for(int i = 0; i < 3; ++i)
        {
            LL tt = t*a[i];
            if(tt <= Max)
            se.insert(tt);
        }
        t = *se.upper_bound(t);
        if(t == Max)
            break;
    }
    set<LL>::iterator it;
    for(it = se.begin(); it != se.end(); ++it)
        cout<<*it<<endl;

    cout<<"answer = "<<se.size()<<endl;
}
int main(void)
{
    Find(Max);
    return 0;
}

输出 前 1905 个幸运数

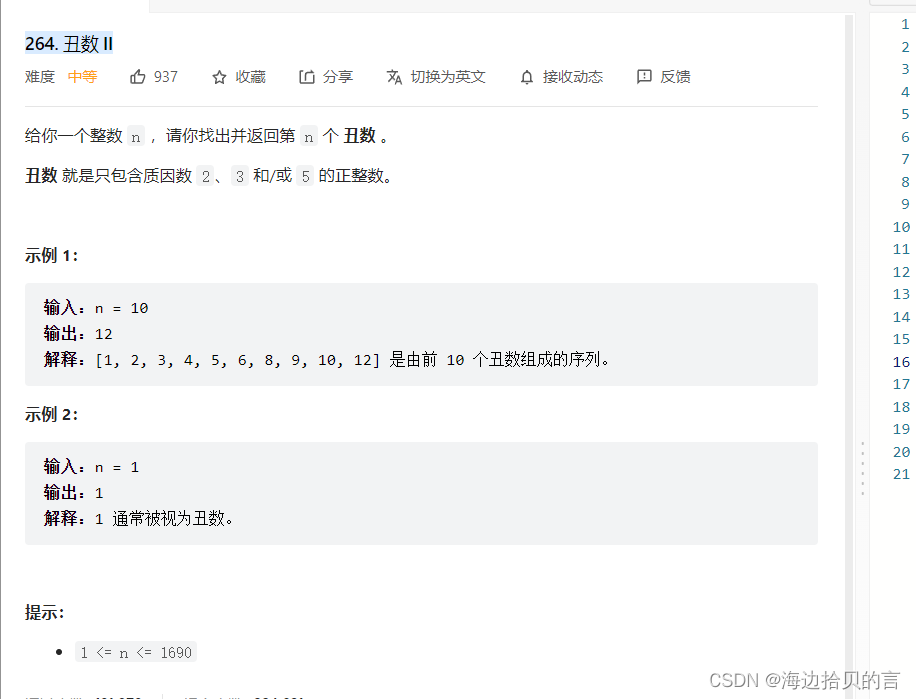
LeetCode264. 丑数 II 链接

方案2

动态规划
具体解析去看leetcode

class Solution {
public:
    int nthUglyNumber(int n) {
        int cnt = 0;
        set<long long > s;
        vector<long long > dp(1691,0);
        dp[0] = 1;
        int p1,p2,p3;
        p1 = p2 = p3 = 0;
        for(int i = 1;i <= n; ++i) {
            int t = min(dp[p1]*2,min(dp[p2]*3,dp[p3]*5));
            dp[i] = t;
            if(dp[p1]*2 == t) p1++;
            if(dp[p2]*3 == t) p2++;
            if(dp[p3]*5 == t) p3++;
            // cout<<t<<endl;
        }
        return dp[n-1];

    }
};