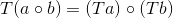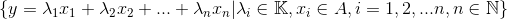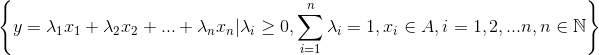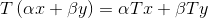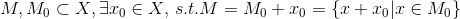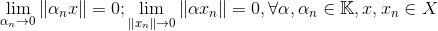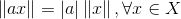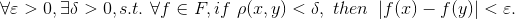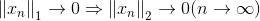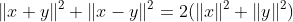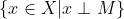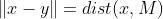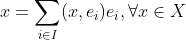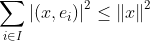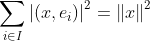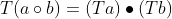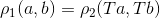1 线性空间
满足加法数乘的线性运算
- 线性包spanA:
- 凸包coA:
即有限凸组合组成的集合 - 同构:
是双射且
- 线性流形:线性子空间对某个向量的平移,
2 赋范线性空间
2.1 定义
1.准范数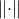
[1]正定性: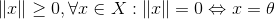
[2]三角不等式: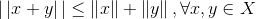
[3]偶性: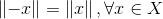
[4]连续性:
2.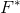
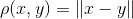
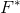
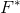
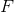
3.范数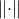
[1]正定性: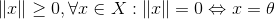
[2]三角不等式: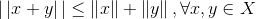
[3]齐次性:
4.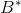
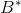
2.2 Araela-Ascoli 定理
F是C(M)的一个子集,M是距离空间
- 一致有界:
- 等度连续:
- F列紧
F一致有界,等度连续.
2.3 等价范数
比
强:
- 范数等价:
比
强且
比
强
2.4 有限维空间
-
Riesz引理:
是赋范线性空间
的真闭子空间,
,存在
,满足
,且对一切
,有
-
局部列紧性:赋范线性空间E是有限维的,当且仅当E中的单位球是列紧的。
3 内积空间
3.1 定义
- 正定性;共轭对称性;共轭齐次性;加法等式。
- 赋范线性空间能引入内积
它的范数满足平行四边形法则
- 完备的内积空间称为Hilbert空间
3.2 正交与正交基
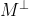
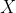
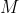
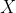
[正交分解(不知道这个讲义为啥将这两部分分开)]
1.M是Hilbert空间X中的一个非空闭凸集,对于
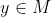
2.M是Hilbert空间X中的一个闭子空间,对于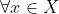
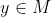
3.M是Hilbert空间X中的一个真闭子空间,对于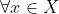
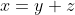
4.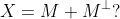
3.3 Bessel不等式
:;
;
是
的闭线性子空间;
- 设
是Hilbert空间,则
。
Define: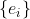
Bessel不等式:
Parseval等式:
3.4 Hilbert空间的同构
同构: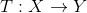
线性同构:同构+线性,即双射且
等距同构:线性同构+等距,即双射且