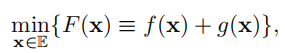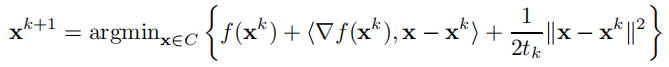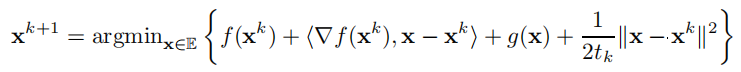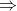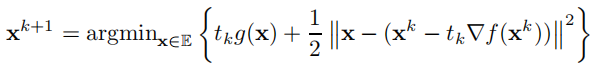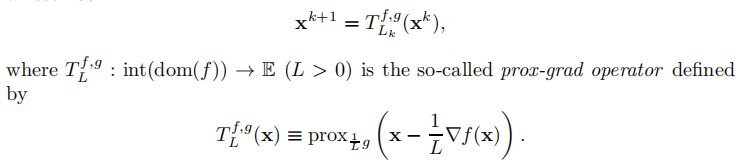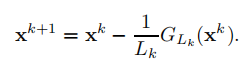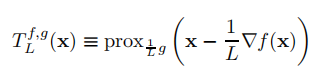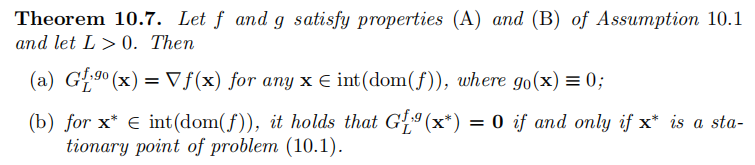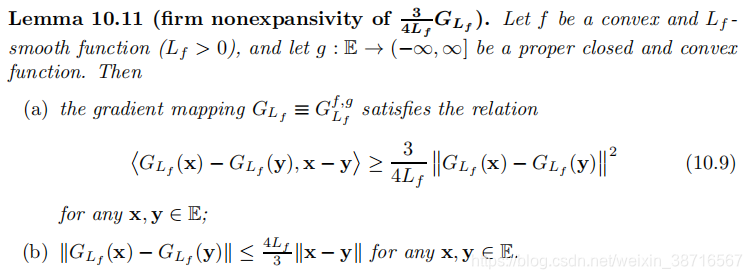参考文献：first-order methods in optimization: Amir Beck

Underlying  Space:Euclidean norm

1 The Composite Model

本章主要考虑的复合函数模型及假设如下：

2  The Proximal Gradient Method

考虑以下问题（)：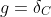

投影梯度方法：

等价于

回到更一般的复合函数问题，有：

这里的步长是取定的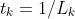。介绍一个新的算子符号：

下面我们非凸和凸两种情况讨论这种算法的收敛性:

3  Analysis of the Proximal Gradient Method—The Nonconvex Case

3.1 Sufficient Decrease

讨论非凸情形下的充分下降性：

易证。

3.2 The Gradient Mapping

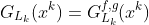
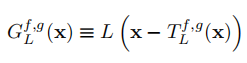
其中，可以看作梯度的推广。根据

很容易得到该式。  此时若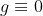，后半部分为梯度（与红字相呼应），如定理10.7 所述:

我们把G看作一个度量，实际上同原始的梯度相同，一开始都是<0，但到达稳定点时，等于0。

探索G的性质，实际上10.7也属于G的性质：

3.3 Convergence of the Proximal Gradient Method—The Nonconvex Case

步长选取：

4  Analysis of the Proximal Gradient Method—The Convex Case