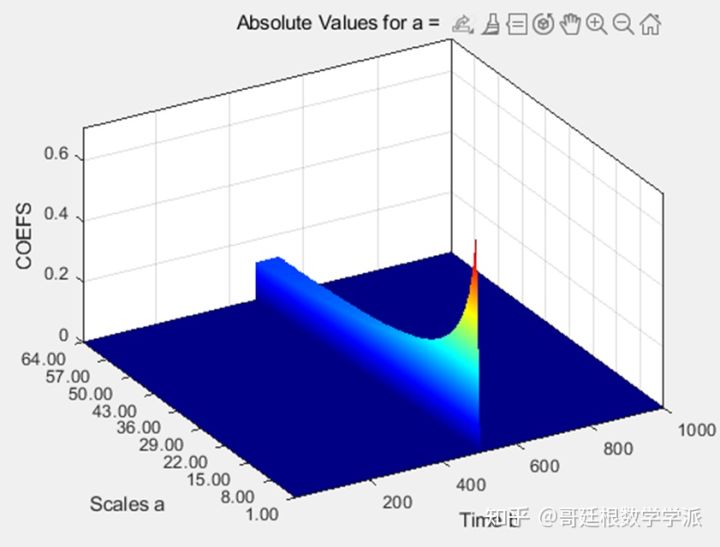
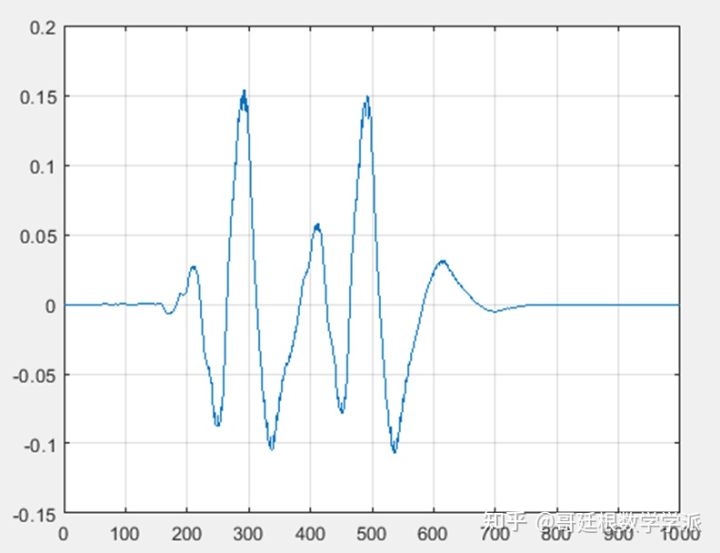
连续小波变换CWT是一种冗余变换,CWT系数取决于所用的小波,所以理解起来稍微有些困难。为更好地理解CWT系数,本文从简单信号和简单小波开始分析。小波擅长检测信号的不连续性或奇异点,信号的突变点处具有较大的绝对值系数。首先设置一个移位脉冲信号,脉冲发生在第500点的位置。
x = zeros(1000,1);
x(500) = 1;
选择了一个简单信号,自然要选择一个简单小波,那自然是haar小波了
在1-128的尺度范围上使用Haar小波计算CWT
CWTcoeffs = cwt(x,1:128,'haar');CWTcoeffs是一个大小为128×1000的矩阵,矩阵的每一行都包含一个尺度的 CWT系数。由于CWT的尺度为1:128,因此共128 行,矩阵的列维度与输入信号的长度相同。
看一下CWT的时间-尺度谱
cwt(x,1:128,'haar','plot');
colormap jet; colorbar;
还可以绘制一下3D图,为了便于观察,减小尺度范围
cwt(x,1:64,'haar','3Dplot'); colormap jet;检查移位脉冲信号的CWT,可以看到CWT较大的系数集集中在时间-尺度平面以点 500 为中心的小尺度的狭窄区域。随着尺度的增加,CWT较大的系数集变宽,但仍以点 500 为中心。如果跟踪该区域的边界,类似于下图
该区域成为Haar小波在点500处的“影响锥”。要理解“影响锥”,假设一个小波的支撑区间为[-C, C],将小波移动 b并缩放尺度a ,支撑区间变为[-Ca+b, Ca+b]。对于移位脉冲δ(t−τ),CWT 系数仅在 τ 附近的区间非零,该区间等于小波在每个尺度上的支撑区间,可以通过移位脉冲的CWT表达式来理解:
对于脉冲信号而言,可以通过选定几个尺度绘制CWT系数看一下
“影响锥”取决于小波种类。以两个移位脉冲的叠加δ(t−300)+δ(t−500)为例子,在这种情况下,使用具有4阶消失矩db4小波。下图显示了使用 db4小波对第300和第500点的影响锥。
查看第20尺度的第400个点,在该尺度下,可以看到两个“影响锥”都没有与第400点重叠。因此, CWT系数在该点和该尺度上为零,可以看一下小波系数图:
接下来,查看尺度80处第400点,在尺度80处,第300 和 第500点的影响锥都包括第400点,即使信号在第400点处为零,仍会在该尺度下获得非零的CWT 系数。看一下小波系数图:
在前面的例子中,CWT 系数在信号突变点附件较大,这种检测信号不连续性的能力是小波变换的优势。前面的例子还证明了CWT的系数在较小尺度上最更好的不连续定位能力。
下面看一个稍微复杂的例子,构建一个由突变和平滑振荡组成的信号,该信号是一个2Hz正弦曲线,带有2个不连续点
N = 1024;
t = linspace(0,1,1024);
x = 4*sin(4*pi*t);
x = x - sign(t - .3) - sign(.72 - t);
plot(t,x); xlabel('t'); ylabel('x');
grid on;
注意 t=0.3和 t=0.7附近的不连续性,使用 sym4小波绘制 CWT
CWT可以检测出信号中的突变点和振荡部分,突变点会影响所有尺度的CWT 系数,并清楚地与小尺度上更平滑的信号特征区分开来。另一方面,2Hz 正弦波的最大值和最小值在较大尺度的 CWT 系数中很明显,而在小尺度上不明显。
最后总结一下,理解CWT的系数时,一个点的CWT系数可能会受到远离该点的信号值的影响。必须考虑小波在特定尺度上的支撑区间,并非所有小波的支撑区间都相同。例如,Haar小波在所有尺度上的支撑区间都小于 sym4 小波。此外小波对于检测信号的突变非常有用,信号中的突变会产生相对较大的小波系数(以所有尺度的不连续点为中心)。最后,平滑信号在小波与信号特征最相关的尺度上产生相对较大的小波系数。