本文介绍GMM-HMM语音识别系统，虽然现在主流端到端系统，但是传统识别系统的学习是很有必要的。阅读本文前，需要了解语音特征提取、混合高斯模型GMM、隐马尔科夫模型HMM的基础知识（可以参考我的前几篇文章）。笔者能力有限，如有错误请指正！

GMM-HMM语音识别系统的框架：

1. 数据准备：数据源准备(wav/txt)、其他数据(词典、音素集等)、验证集、测试集
2. 特征提取：MFCC
3. 单音素GMM-HMM训练：单音素为三音素提供对齐
4. 三音素GMM-HMM训练
5. 解码

语音识别的几个概念：

• 对齐：音频和文本的对应关系
• 训练：已知对齐，迭代计算模型参数
• 解码：根据训练得到的模型参数，从音频推出文本

基于孤立词的GMM-HMM语音识别

问题简化，我们考虑(0-9)数字识别。整体思路：

• 训练阶段，对于每个词用不同的音频作为训练样本，构建一个生成模型$P(X|W)$，W是词，X是音频特征（MFCC、Fbank参考这篇博客）
• 解码阶段：给定一段音频特征，经过训练得到的模型，看哪个词生成这段音频的概率最大，取最大的那个词作为识别结果。

${\mathbf{X}}_{test}$测试特征，$P_w(\mathbf{X})$是词$w$的概率模型，$vocab$是词表：

$$answer=\underset{w\in \text{ vocab }}{\mathrm{argmax}}{P}_w\left({\mathbf{X}}_{\text{test }}\right)$$

假设我们给每个词建立了一个模型：$P_{one}(X),P_{two}(X)...$，计算在每个词上的概率，选择所有词中概率最大的词作为识别结果。这样会有几个问题：用什么方法进行建模：DNN，GMM?这些够可以进行建模，但是语音任务的特点是序列性，不定长性，很难使用DNN、GMM直接进行建模。为了解决这些问题，我们可以利用HMM来进行序列建模。

语音是一个序列，$P_w(X)$可以用HMM的概率问题来描述，并且其中的观测是连续概率密度分布，我们可以为每个词建立一个GMM-HMM模型。

建模

语音识别中的GMM，采用对角GMM（协方差为对角阵），因为一般我们使用MFCC特征，MFCC特征各维之间已经做了去相关处理，各维之间相互独立，直接使用对角阵就可以描述，而且对角GMM参数量小。

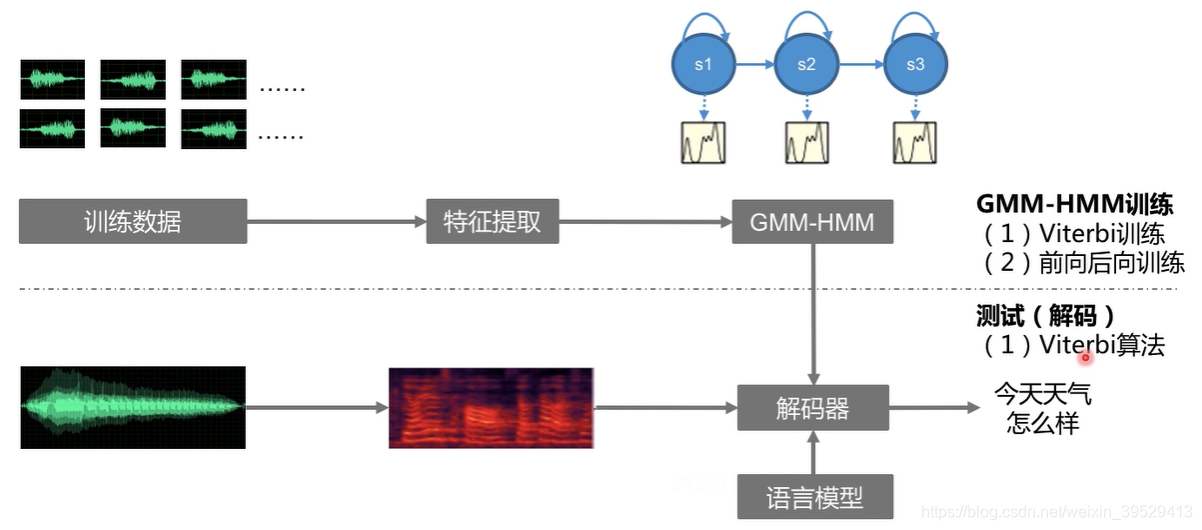
语音识别中的HMM，采用3状态，左右模型的HMM：

• 为什么采用3状态？这是前人大量实验给出的经验值；
• 左右模型的HMM：对于每个状态，它只能跳转到自身或者下一个状态。类似于人的发音过程，连续不可逆。

HMM、GMM语音识别中如何结合？

对于每个状态有一个GMM模型，对于每个词有一个HMM模型，当一段语音输入后，根据Viterbi算法得到一个序列在GMM-HMM上的概率，然后通过Viterbi回溯得到每帧属于HMM的哪个状态（对齐）。

训练

GMM-HMM模型参数：

• 初始化参数（左右HMM）：这参数没必要
• 转移参数：自跳或者跳向下一个（两个参数）
• 观测参数：混合系数、均值、方差

Viterbi训练

1. E步
   • Viterbi算法得到最优的状态序列（对齐），也就是在t时刻处于状态i上的概率（非0即1）
   • GMM模型中在t时刻处于状态i第k个GMM分量的概率
2. M步
   • 更新转移参数、GMM参数（混合系数、均值、方差）
3. 重复E、M步

如何初始化GMM-HMM模型的参数？把语音进行均等切分，给每个状态分配对应的特征，然后去估计初始化的参数。

前向后向训练（Baum-Welch训练）

1. E步
   • 通过前向后向算法得到在时刻t处于状态i的概率
   • 在时刻t处于状态i且为GMM第k个分量的概率
2. M步
   • 更新转移参数、GMM参数（混合系数、均值、方差）
3. 重复E、M步

Viterbi和Baum-Welch学习算法的详细内容参考我之前的文章。

解码

输入：各个词的GMM-HMM模型，未知的测试语音特征。

输出：哪个词。

主要关键点：对所有的词，如果计算$P_w(X_{test})$。可以通过：前向后算法，或者Viterbi算法（可以回溯到最优的状态序列），一般采用Viterbi算法。

解码主要在图上做，我们现在看one two两个数字识别问题：

构建HMM模型的拓扑图，下图是紧凑的解码图：

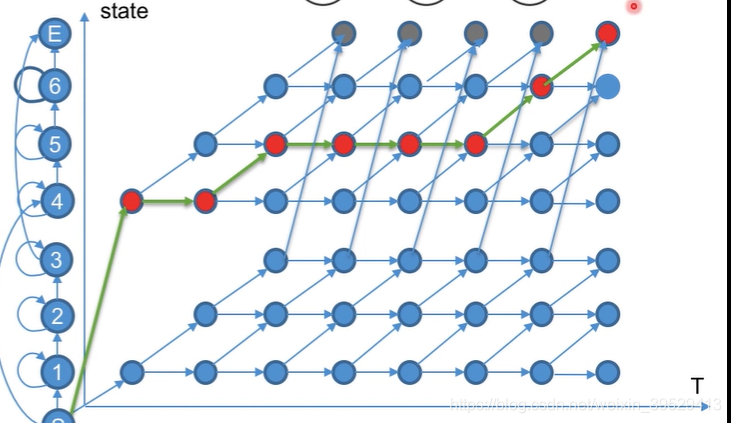
通过Viterbi算法，找过最优的路径得到最终输出的词。那么如果我们需要对连续的多个词识别，需要如何建模？

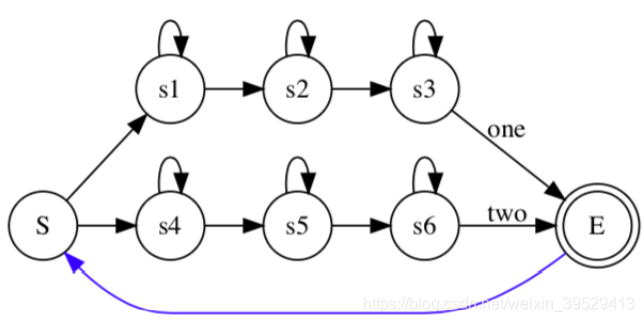
我们只需要再拓扑图上加一个循环连接，对于孤立词，如果达到了识别状态就结束了，对于连续词，如果达到了结束状态，就继续识别下一个词。每个HMM内部还是采用Viterbi算法，在每个时刻对于每个状态选择一条最大概率的路径。因为是并行的，在某个时刻，可能同时会有多个词达到结束状态，分别对应着一段路径，然后又要同时进行下一个词的识别，那么为了避免多余的计算，采用和Viterbi一样的思路，只选取最大概率的路径，扔掉其他。

基于单音素的GMM-HMM语音识别系统

孤立词系统的缺点：

• 建模单元数、计算量和词典大小成正比
• OOV（out of Vocabulary）问题，训练中没有这个词，测试中存在这个词；
• 词的状态数对每个词不用，长词使用的状态数更多

为了克服上边的问题，采用音素建模。每个音素使用3状态结构：

问题：如果一句话中包含多个单词？

这个采用和上述相同的方法，加入循环结构，当到达结束状态时进行下一个词的识别。

基于三音素的GMM-HMM语音识别系统

单音素缺点：

• 建模单元数少，一般英文系统的音素数30-60个，中文的音素数100个左右；
• 音素的发音受上下文影响，比如：连读、吞音。

可以考虑音素的上下文，一般考虑前一个/后一个，称为三音素，表示为A-B+C。比如：KEEP K IY P => #-K+IY, K-IY+P, IY-P+#。

问题1：假设有N个音素，一共有多少个三音素？$N^3$

问题2：有的三音素训练数据少或者不存在，怎么办？

问题3：有的三音素在训练中不存在，但在测试中有怎么办?

问题2和问题3通过参数共享解决，下文将介绍决策树。

参数共享

共享可以在不同层面：

• 共享高斯模型：所有状态都用同样的高斯模型，只是混合权重不一样；
• 共享状态：允许不同的HMM模型使用一些相同的状态；
• 共享模型：相似的三音素使用同样的HMM模型。

笔者主要介绍共享状态，可以采用自顶向下的拆分，建立决策树来聚类。

三音素决策树

决策树是一个二叉树，每个非叶子节点上会有一个问题，叶子节点是一个绑定三音素的集合。绑定的粒度为状态（A-B+C和A-B+D的第1个状态绑定在一起，并不表示其第二第三个状态也要绑定在一起），也就是B的每个状态都有一颗小的决策树。

问题集

常见的有：

• 元音 AA AE AH AO AW AX AXR AY EH ER …
• 爆破音 B D G P T K
• 鼻音 M N NG
• 摩擦音 CH DH F JH S SH TH V Z ZH
• 流音 L R W Y

问题集的构建：语言学家定义，Kaldi中通过自顶向下的聚类自动构建问题集。

决策树构建

初始条件类似图中的根节点，"*-zh+*"，从问题集中选择合适的问题，分裂该节点，使相近的三音素分类到相同的节点上。假设根节点所有三音素对应的特征服从一个多元单高斯分布，可以计算出该单高斯分布的均值和方差，则可以计算出该节点任意一个特征在高斯上的似然。

模型：假设其服从单高斯分布，并且各维独立，也就是对角GMM
$$\mathrm{Pr}[x]=\frac{1}{{\prod }_{k=1}^N{\left(2\pi {\sigma }_k^2\right)}^{1/2}}\prod _{k=1}^N\exp \left(-\frac{1}{2}\frac{{\left(x_k-{\mu }_k\right)}^2}{{\sigma }_k^2}\right)$$
似然
$$\begin{array}{rl}L(S)& =-\frac{1}{2}\sum _{i=1}^m\left[\sum _{k=1}^N\log \left(2\pi {\sigma }_k^2\right)+\sum _{k=1}^N\frac{{\left(x_{ik}-{\mu }_k\right)}^2}{{\sigma }_k^2}\right]\\ & =-\frac{1}{2}\left[m\sum _{k=1}^N\log \left(2\pi {\sigma }_k^2\right)+m\sum _{k=1}^N\frac{{\sigma }_k^2}{{\sigma }_k^2}\right]\\ & =-\frac{1}{2}\left[mN(1+\log (2\pi ))+m\sum _{k=1}^N\log \left({\sigma }_k^2\right)\right]\end{array}$$

假设通过某个问题将该节点的三音素对应的特征分成两部分(l 和 r)，则这两部分的似然和为：
$$L\left(S_l\right)+L\left(S_r\right)=-\frac{1}{2}mN(1+\log (2\pi ))-\frac{1}{2}\left[m_l\sum _{k=1}^N\log \left({\sigma }_{lk}^2\right)+m_r\sum _{k=1}^N\log \left({\sigma }_{rk}^2\right)\right]$$
分裂前后的似然变化（增益）为：
$$L\left(S_l\right)+L\left(S_r\right)-L(S)$$
似然增益越大，说明分裂后两部分数据之间的差异越大，则应该使用两个单独的GMM分别建模，则选择似然增益最大的问题进行划分（最优问题）。根节点一份为2后，递归执行该算法直至达到一定终止条件，通常是分裂达到一定数量的叶子节点或者似然增益已经低于一定阈值。

总结

1. 初始状态（单因素系统对齐，一个根节点）
2. 选择一个节点，从问题集中选择似然增益最大的问题作为该节点问题，建立该节点左右子节点，并将该节点一分为二
3. 重复2，直至满足一定的终止条件。

基于GMM-HMM语音识别系统流程

1. 数据准备：音素列表、词典、训练数据
2. 特征提取：MFCC特征
3. 单音素GMM-HMM：Viterbi训练
4. 三音素GMM-HMM：三音素决策树、Viterbi训练
5. 解码

问题：为什么先做单音素训练？

通过单音素模型上Viterbi算法得到与输入对应的最佳状态序列（对齐）。

参考：

https://blog.csdn.net/Magical_Bubble/article/details/90408095

https://zhuanlan.zhihu.com/p/63753017