在这篇文章中，我们将探索欧拉公式，解释它是什么，它从哪里来，并揭示它神奇的性质。

欧拉公式是什么？

欧拉公式是欧哈德·欧拉在十八世纪创造的，是数学界最著名、最美丽的公式之一。之所以如此，是因为它涉及到各种显然非常不同的元素，比如无理数e、虚数和三角函数。让我们看看它是什么样的：

• 欧拉公式

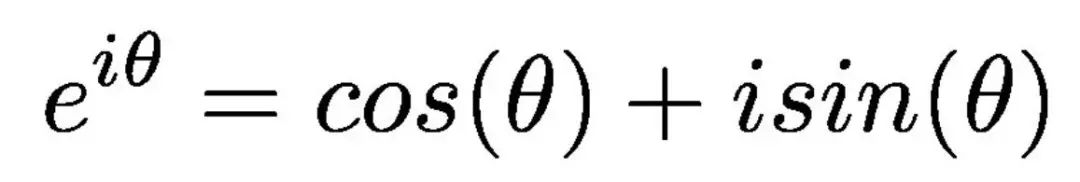
正如我们所看到的，左边是e，右边是cos和sin三角函数，两边都有虚数i。在我们从微积分和几何的角度研究这个公式之前，让我们先看看这个疯狂的关系是从哪里来的。

欧拉公式的历史

1714年，英国物理学家和数学家罗杰·柯茨在一个公式中建立了对数、三角函数和虚数之间的关系。二十年后，莱昂哈德·欧拉用指数函数代替对数得到了同样的公式。柯茨的公式如下：

• 罗杰·柯茨公式

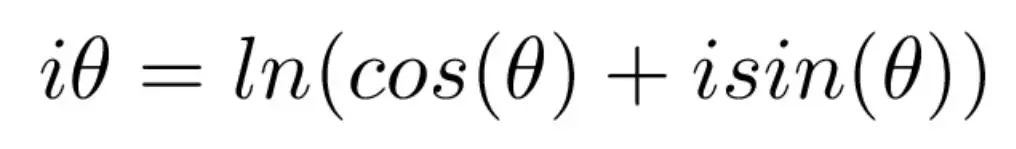
从柯特公式到欧拉公式我们只需要在两边都应用指数。为了将欧拉公式转化为柯特公式，我们用对数反转这个过程。奇怪的是，每个公式的作者都没有看到它的几何含义，而这正是从这些公式中可以得到的最令人着迷的东西之一。下图展示了一个复平面，我们将在这里看到这些几何内涵。

• 复平面，周长为1

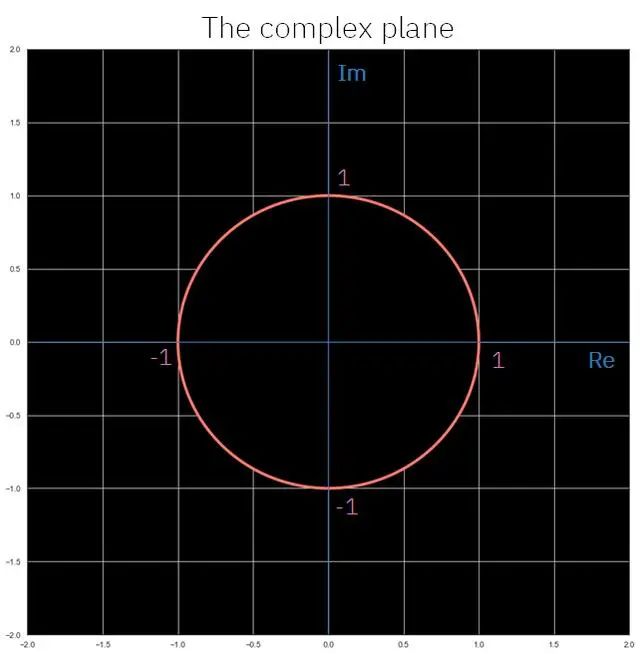
在此之前，你应该知道，如果我们把欧拉公式的值特殊化为：θ = π，我们得到了著名的欧拉恒等式。

欧拉恒等式

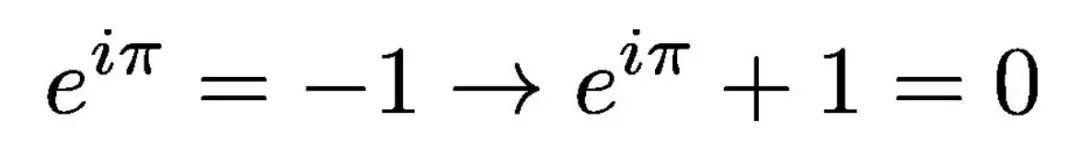
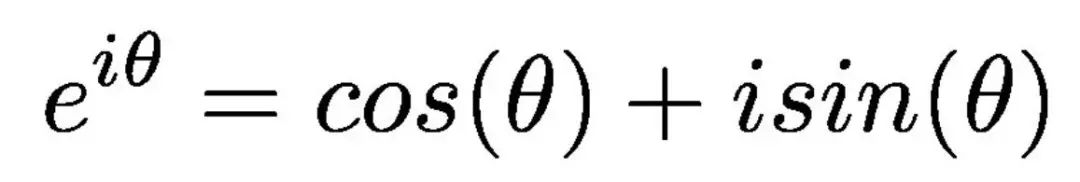
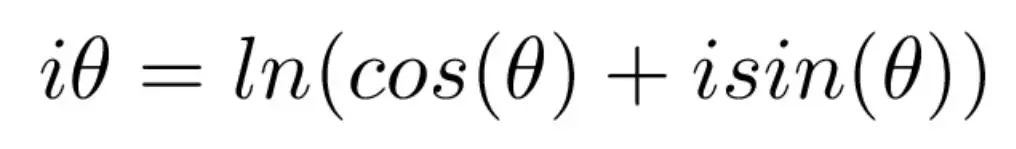
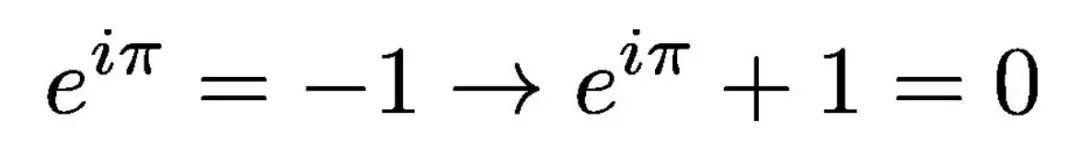如前所述，如果我们设θ = π，欧拉公式就变成了欧拉恒等式。 现在我们知道了欧拉公式和欧拉等式是什么，让我们把前者分解成单独的元