前面我们已经深入讨论了二分类任务的评估,接下来我们看一下对多分类问题的指标评估:多分类问题的所有指标基本上都来自二分类指标,但是要求对所有类别进行平均。
多分类的精度被定义为正确分类的样本所占的比例,同样,如果类别是不平衡的,精度比不是很好的评估度量。一般来说,多分类问题比二分类问题更加难以理解。除了精度,常用的工具也有混淆矩阵和分类报告,我们在上一节二分类的例子中出现过。下面我们将这两种详细的评估方法应用于对digits数据集中10种不同手写数字进行分类任务:
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
from sklearn.datasets import load_digits
digits = load_digits()
y = digits.target
from sklearn.metrics import accuracy_score
x_train, x_test, y_train, y_test = train_test_split(digits.data, y, random_state=0)
lr = LogisticRegression().fit(x_train, y_train)
pred = lr.predict(x_test)
print("Accuracy value is: {:.3f}".format(accuracy_score(y_test, pred)))
print("Confusion matrix:{}".format(confusion_matrix(y_test, pred)))
运行后其结果为:

digits数据集的预测精度和混合矩阵结果
从运行结果可以看出,其精度为0.976,这个精度已经很高了,混淆矩阵提供了更多的细节,与二分类的情况类似,每一行对应于真实标签,每一列对应于预测标签。
对于其视觉显示代码如下:
score_image = mglearn.tools.heatmap(confusion_matrix(y_test, pred), xlabel='predicted label',
ylabel='True label', xticklabels=digits.target_names,
yticklabels=digits.target_names, cmap=plt.cm.gray_r, fmt="%d")
plt.title("Confusion_matrix")
plt.gca().invert_yaxis()
运行结果为:
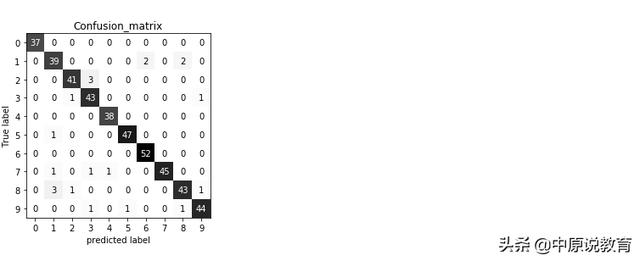
10个数字分类任务的混淆矩阵
从运行结果来看,第一个类别(数字0),包含了37个样本,所有这些样本都被划分为类别0(即没有假反例:因为混淆矩阵中的第一行其他所有元素都为0;另外同时其他数字没有被误分为0,这是混淆矩阵第一列中其他所有元素都为0(类别0也没有假反例))。
类别2(数字1)43个样本,其中39个被划分为1,分别有2个被划分成了6和8(假反例),有5个假正例,分别为1个5和1个7还有3个8。其他类别的样例分析类似。
利用classification_report函数分别计算每个类别的准确率、召回率以及f-分数
print(classification_report(y_test, pred))
from sklearn.metrics import classification_report
运行后结果为:
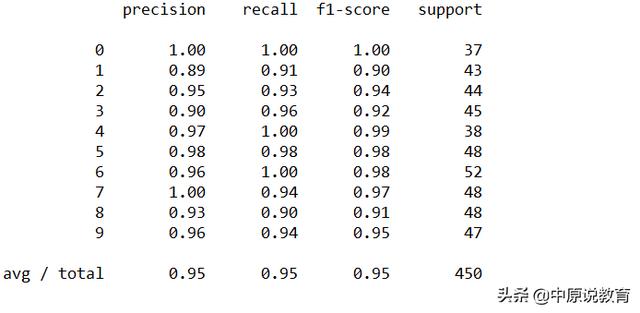
结果10个数字分类任务的classification_report
正如所料,类别0的准确率和召回率都是完美的1,因为这个类别中没有混淆;类别7的争取率为1,因为没有其他类别被误分为7,但是其回收率为0.74,因为有1个7被误分为1,说明有假正例。同理方式用来分析其他类。
对于多分类问题中的不平衡数据集,最常用的指标就是多分类版本的f-分数,多数分类f-分数的背后思想是,对于每个类别计算一个二分类f-分数,其中该类别是正类,其他所有类别是反类。然后,使用以下策略之一对这些f-分数进行平均。
“宏”(macro)平均:计算未加权的按类别f1-分数,他对所有类别给出相同的权重,无论类别中的样本量大小。
“加权”(weight)平均:以每个类别的支持作为权重来计算按类别f1-分数的平均值,分类报告中给出的就是这个值。
“微”(micro)平均:计算所有类别中假正例、假反例和真正例的总数,然后利用这些计算来计算准确率、召回率和f1-分数。
如果你对每个样本等同看待,那么推荐用“微”平均f1-分数;如果对每个类别等同看待,则推荐用“宏”平均f1-分数。
print("Micro average f1 score: {:.3f}".format(f1_score(y_test, pred, average="micro")))
print("Macro average f1 score: {:.3f}".format(f1_score(y_test, pred, average="macro")))
运行后其f1-分数分别为:
Micro average f1 score: 0.953
Macro average f1 score: 0.954
回归指标:对回归问题可以像分类问题一样进行详细评估。如:对目标值估计过高与目标值估计过低进行对比分析。但是,对于我们见过的大多数应用来说,使用默认R²就足够了,它由所有回归其的score方法给出。业务决策有时是根据均方误差或平均绝对误差做出的,这会鼓励人们使用这些指标来调节模型。但是一般来说,我们认为R²是评估回归模型更直观的指标。