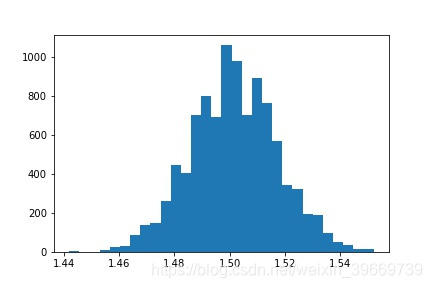
推断统计是指用样本数量特征推断总体特征 ，在现实生活中，我们只抽取一个样本，计算出一个统计量(样本均值，样本方差，样本比例等）的值，将其作为总体参数的一个估计值，这种方法也称点估计，但是这样做往往不准确，但是我们有了抽样分布的概念，指的是所有估计值的集合，以样本均值为例，由中心极限定理(clt)知，

从均值$\mu$、方差为${\sigma }^2$的任意一个总体中抽取样本容量为$n$的样本，当$n$充分大时，样本均值$\bar{x}$的抽样分布渐进服从均值为$\mu$,方差为$\frac{{\sigma }^2}{n}$的正态分布。

#中心极限定理实现
import numpy as np
import matplotlib.pyplot as plt
random_data=np.random.randint(1,3,10000)
s=[]
for i in range(10000):
    sample=np.random.choice(random_data,1000)
    s.append(sample.mean())
plt.hist(s,bins=30)

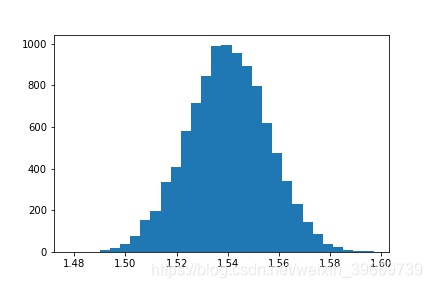
但是样本容量小或者说我们收集到的数据有限时，抽样分布不再服从正态分布，那我们如何做统计推断呢，可以采用bootstrap抽样法，

基本思想是从总体中抽出一个样本，然后从这个样本中进行有放回抽样，抽取若干个样本（一般大于1000且每个样本容量和初始抽取样本容量相同，每个样本计算出样本统计量的值，仍以均值为例，计算出$\overline{x_1},\overline{x_2}\dots \overline{x_n}$，得到均值的抽样分布，此时
总体均值$$\hat{\mu }=\frac{{\sum }_{i=1}^n\overline{x_i}}{n}$$
总体方差$$\widehat{{\sigma }^2}=\frac{{\sum }_{i=1}^n(\widehat{\mu -\bar{x_i}{)}^2}}{n-1}$$
这就是用bootstrap方法去估计总体均值和方差。

# bootstrap实现
np.random.seed(123)
s=np.random.choice(random_data,100)
b=[]
for i in range(10000):
    c=np.random.choice(s,1000)
    b.append(c.mean())
plt.hist(b,bins=30)