这方面在网上各种博客也没有找到相关的好用的总结文章,最近看了几篇文章,总结一下相关的算法。这几篇文章读完,基本上对半监督学习图像分类有一个相对直观的了解。
总结一下这一堆算法的套路:
- 熵最小化
- 一致性正则化
- 正则化
- mixup
- dropout
主要对自己阅读过的几篇论文做一下总结:
- Pseudo-Label : The Simple and Efficient Semi-Supervised Learning Method for Deep Neural Networks
- Virtual Adversarial Training: a Regularization Method for Supervised and Semi-supervised Learning
- Temporal Ensembling for Semi-Supervised Learning
- Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results
- mixup: BEYOND EMPIRICAL RISK MINIMIZATION
- Interpolation Consistency Training forSemi-Supervised Learning
- MixMatch: A Holistic Approach to Semi-supervise learning
- ReMixMatch: Semi-Supervised Learning with Distribution Alignment and Augmentation Anchoring
- FixMatch: Simplifying Semi-Supervised Learning withConsistency and Confidence
这几篇文章是我最近学习这方面资料所已经读过和将要读的一些文章,先看理论知识,然后了解基本的思路之后,再研究代码的实现问题。
算法1:Pseudo-Label : The Simple and Efficient Semi-Supervised Learning Method for Deep Neural Networks
2013年的一篇文章。
基本算法思路
Pseudo-label是将未标注样本预测来率最大的目标类作为看作真实的标签(也就是经过CNN前向传播,最终softmax输出的最大概率对应的类别作为其pseudo label)。
在训练的过程中,每次权重更新之后,重新计算无标注样本的伪标签作为真实的标签,然后使用与有监督训练分类过程中的交叉熵损失函数,同时对于有标注样本与无标注样本的损失函数进行加权处理。
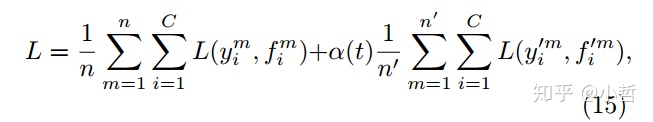
alpha时调节二者权重的系数,如果alpha太大,那么消除了有标注样本的作用; 如果太小,那么半监督学习几乎没有意义,因此设置alpha为下面的分段调整的形式,能够得到更好的效果。
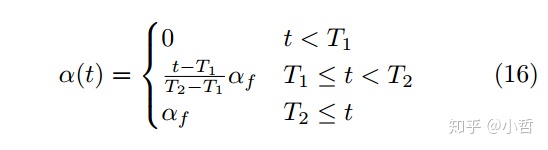
pseudo-label起作用的一些理论依据
- 决策边界应该穿过数据分布的低密度区域
正常的直觉也是这样,当分类决策边界位于数据集的样本低密度区域时,算法能够较好的将数据分割开来,算法分类更加合理,分类准确率更高。
cluster assumption 在这篇2005年的论文中说明了理论。
- 熵正则化
Entropy Regularization在这篇2006年的文章中说明,应用熵正则化可以从无标注数据的最大后验概率估计中受益,通过最小化类概率的条件熵,可以在不进行密度建模的情况下,实现低密度区域的分离。
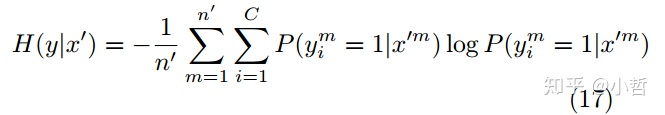
在这个式子中,熵是未重叠的类别的度量,熵越小,随着类别重叠的越小,数据样本的密度就越小。
最大化后验概率估计:
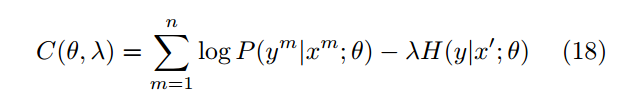
在这个式子中,第一项时有标注样本的概率最大,第二项时对于无标注样本来说的上最小,使得数据点的密度最小。由此可以得到更好的泛化能力。
- 以伪标签作为熵正则化进行训练
分别分析上边的式子(18)与式子(15),18的第一项对应15的第一项,18的第二项对应于15的第二项,因此伪标签的方法等价与熵正则化。
使用伪标签的训练,使得无标注数据样本的熵变得更小,使得决策边界处于数据样本密度更低的位置,分类泛化性能更好。
算法2:Temporal Ensembling for Semi-Supervised Learning
2017年的文章
算法思想
文中主要提出了两个模型第一个是 II model,网络结构以及算法伪代码如下图所示。
- II Model
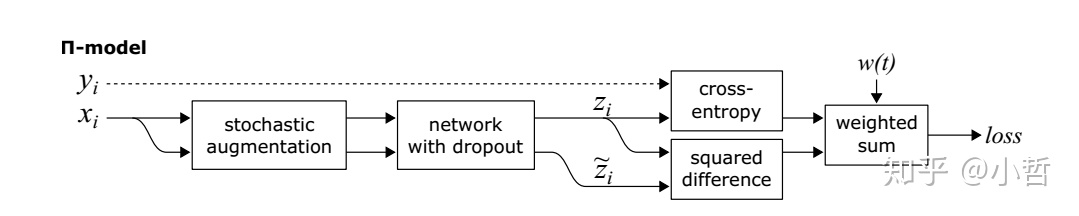
根据以上结构图简要介绍算法的操作流程。
- 训练的过程中,对于一个输入图片经过随机噪声及dropout的网络之后,得到两个不同的输出Zi与Zi‘。
- 损失函数有两部分组成,第一部分评估有标注样本的交叉熵损失函数(仅处理有标注样本),第二部分惩罚两个输入Zi与Zi’的不一致(MSE,处理所有的样本,包括有标注与无标注)
- 损失函数两项的权值采用加权的形式,加权系数为w(t),这个系数随时间变化,在训练刚开始时,我们希望有标注样本占据主要部分,因此交叉熵损失比重应该大,随着训练过程的进行,第二种损失的比重逐渐变大。