目录

问题描述：

EK算法：

算法描述：

伪代码：

例子：

控制台对应输出为：

关键定理证明：

最大流最小割定理：

1推2：

2推3：

3推1：

时间复杂度分析

分析

关键边定义：

时间复杂度计算：

FF算法：

FF算法介绍

FF算法缺陷分析：

问题描述：

G=（V，E）是一个有向图，其中每条边（u，v）有一个非负的容量值c（u，v），而且如果E中包含一条边（u，v），那么图中就不存在它的反向边。在流网络中有两个特殊的结点，源结点s和汇点t，源结点s只会流出不会流进，汇点只会流进不会流出，我们要求的就是从源结点流到汇结点的路径的值之和的最大值

EK算法：

算法描述：

每次从残留网络中找出一条从源结点到汇结点的最短路径，流选为路径中的残存容量，依据流更新残存网络（将每条边的残存容量改为当前容量减去流的大小，并添加对应的反向边，边的容量为流的大小）

重复选最短路径，更新残存网络，直到没有最短路径为止

此时的流累加和即为最大流

由于每次要找的是最短路径，所以需要用BFS找路径

伪代码：

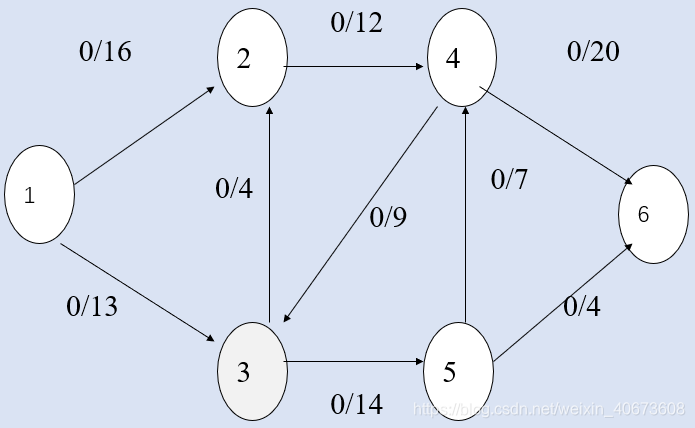
例子：

初始图：

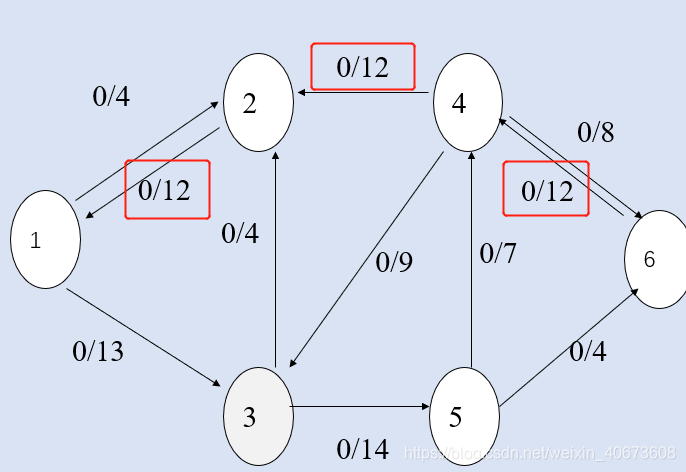
第一次路径1->2->4->6，流大小：12

更新后图为：

第二次路径为1->3->5->6，流大小：4

更新后图为：