前言

原文：原文

准确的自我状态和相对状态估计是完成群体任务的关键前提，例如协作自主探索、目标跟踪、搜索与救援。本文提出了一种名为Swarm-LIO的完全去中心化状态估计方法，适用于空中群体系统，其中每个无人机进行精确的自我状态估计，通过无线通信交换自我状态和相互观测信息，并实时估计与其他无人机的相对状态，所有这些仅基于激光雷达-惯性测量。提出了一种新颖的基于3D激光雷达的无人机检测、识别与跟踪方法，以获取队友无人机的观测数据。然后，将相互观测的测量结果与IMU和LiDAR测量结果紧密耦合，以实时和准确地联合估计自我状态和相对状态。大量真实世界实验表明，该方法对复杂场景具有广泛的适应性，包括GPS受限场景、相机（黑暗夜晚）或激光雷达（面对单一墙壁）的退化场景。与运动捕捉系统提供的真实值相比，结果显示出厘米级的定位精度，优于其他先进的单无人机系统的激光雷达-惯性里程计。

一、介绍

多机器人系统，特别是空中群体系统，在许多方面具有巨大潜力，如自主探索[1]、[2]、目标跟踪[3]、搜索和救援等。得益于其出色的团队合作能力，群体系统即使在单个无人机的退化环境中也能完成复杂场景下的任务。对于单个无人机系统，准确的自我定位[4]-[7]是避障[8]-[10]和飞行控制[11]的先决条件。对于空中群体，鲁棒、准确的自我和相对状态估计[12]同样起着至关重要的作用。对于群体来说，要完成合作任务，群体中的每架无人机都需要实时、精确地进行自我定位，并且始终保持对其他无人机状态的了解。

最近关于空中群体的研究主要集中在协作规划[13]-[15]上，而对群体系统的自我和相对状态估计的研究仍然存在很大差距。在室外场景中，通常采用GPS和RTK-GPS[16]、[17]。而在GPS拒绝的地方，如室内场景，运动捕捉系统[15]、视觉（惯性）里程计[14]、[18]或激光雷达（惯性）里程计[1]、[19]方法更受青睐。此外，超宽带（UWB）也在[13]、[20]中被采用，以产生鲁棒的定位结果。尽管RTK-GPS、运动捕捉和带有锚点的UWB[21]具有很高的精度，但它们依赖于笨重、额外的设备，并且会导致繁琐的安装工作。此外，这些提到的方法使整个系统变得集中化，容易受到单点故障（SPOF）的影响。相机因其轻巧、低成本和丰富的颜色信息而被广泛使用，但它容易受到光照不足的影响，缺乏直接的深度测量，导致在计算3D测量时计算复杂性高。此外，相机的深度测量范围相当有限。无锚点的UWB也是低成本和轻巧的。然而，它只能提供一维距离测量，精度相当有限（通常为米级），这可能会降低整个群体系统的总体精度。

与相机和无锚点UWB相比，激光雷达可以提供准确的3D测量，并且对光照变化也具有鲁棒性。即使在黑暗场景中，例如地下隧道，激光雷达也可以帮助进行准确的定位和制图[18]。近年来，一些成本效益高的固态激光雷达，如Livox1，已经在市场上出现，这显著扩大了基于激光雷达的研究范围。在本文中，我们提出了一种基于激光雷达-惯性测量的鲁棒、实时和去中心化的群体里程计。主要贡献如下：

• 提出了一种新颖的基于3D激光雷达的无人机检测、识别和跟踪方法，提供用于自我和相对状态估计的准确3D相互观察测量。每架无人机都附有反光带，以便通过激光雷达点的反射率值可靠高效地检测队友无人机。然后通过卡尔曼滤波器跟踪检测到的队友无人机，并与共享网络接收到的轨迹匹配，以获得队友的身份及其初始相对状态。
• 一个完全去中心化、稳健、数据高效且计算高效的自我状态和相对状态估计框架。在该框架中，每个无人机只需交换其自我状态和队友观测信息，这需要极低的通信带宽。相互观测的测量结果与激光雷达和IMU测量结果在误差状态迭代卡尔曼滤波（ESIKF）[22]框架下紧密耦合，以实现稳健、准确且同步的自我状态和相对状态估计。
• 低成本、去中心化的硬件和软件框架。传感器和计算资源完全在机载系统上，包括Livox激光雷达、IMU和机载计算机。通信通过标准网络模块上的Ad-Hoc网络实现。
• 在广泛的真实世界实验中实施和验证所提出的方法，涵盖室内（见图1）、户外和退化场景。

二、相关工作

与基于学习的检测方法 [12]、[24] 相比，我们在每架无人机上附加反光带，并利用激光雷达传感器测量的反射率来检测队友无人机。与 [12]、[14] 不同，我们提出了一种从粗到细的校准方法，以获得无需任何初始猜测的准确全局外参转换。通过轨迹匹配获得的粗略校准结果被输入 ESIKF 进行进一步的在线细化，同时估计自我状态。与集中式系统中无人机交换地图信息 [19]、[21]、[25] 相比，我们的系统完全去中心化，不会遇到单点故障问题，且通信效率高，只交换自我状态和相互观察信息。

三、方法

A. 问题表述

为了帮助理解所提出的系统，我们在这里定义了一些重要的符号。$X_i$，${\hat{X}}_i$，${\tilde{X}}_i$，${\bar{X}}_i$ 分别代表无人机 $i$ 的真实、预测、更新和测量状态。$t_{ik}$ 表示无人机 $i$ 的第 $k$ 次 ESIKF 状态更新的时间戳。

考虑一个由 $N$ 架无人机组成的空中群体系统，每架无人机携带一个激光雷达和一个惯性测量单元（IMU），状态估计被分解为两部分。第一部分是自我状态估计。每架无人机，这里为了方便起见选择无人机 $i$，需要估计其自身在全局框架 $G_i$ 中的位置 ${\mathbf{p}}_i\in {\mathbb{R}}^3$ 和姿态 ${\mathbf{R}}_i\in SO(3)$。由于 IMU 测量与未知且时变的偏差耦合，陀螺仪偏差 ${\mathbf{b}}_{gi}\in {\mathbb{R}}^3$ 和加速度计偏差 ${\mathbf{b}}_{ai}\in {\mathbb{R}}^3$ 应被校准。此外，每个全局框架中的重力向量 ${\mathbf{g}}_i\in {\mathbb{R}}^3$ 也应该被估计。

然后，为了估计基于交换的自我状态信息的其他队友无人机的相对状态，每架无人机需要估计全局外参转换。最后，为了提供其他队友的相互观察，每架无人机 $i$ 需要检测、识别和跟踪任何其他队友 $j$，其在自身机体框架中观察到的位置用 ${\mathbf{b}}_{p_{ij}}$ 表示。

B. 框架概述

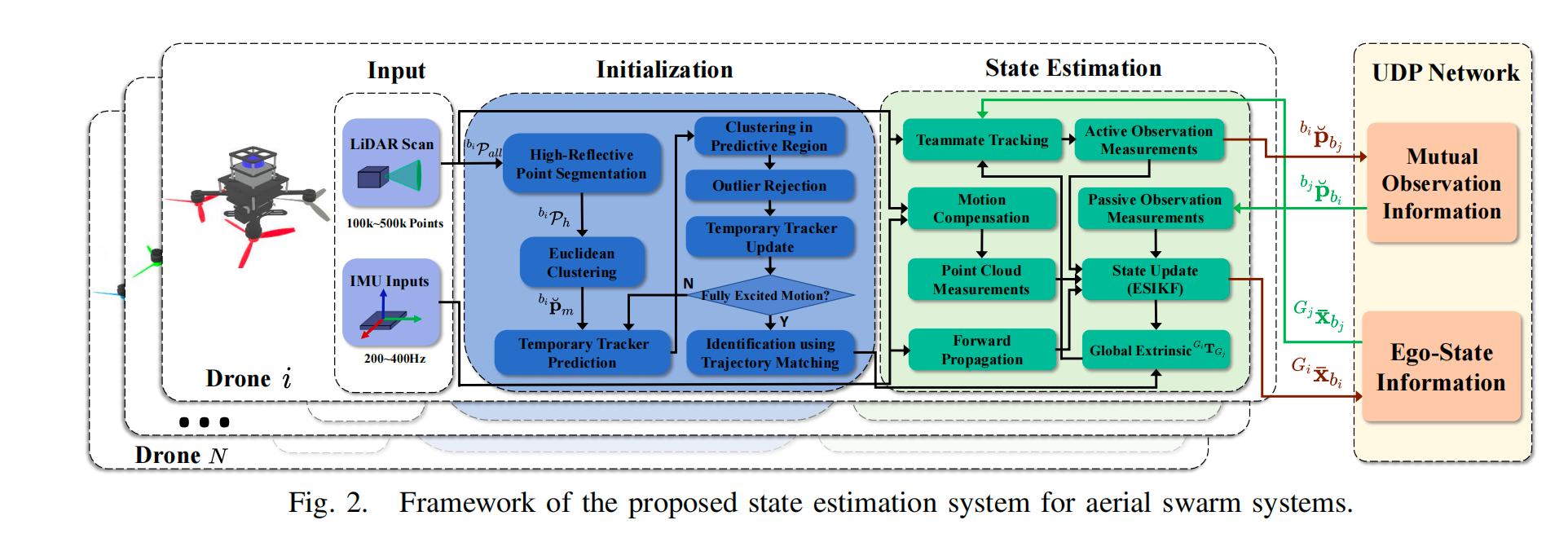
在群体系统中，每架无人机运行相同框架。图 2 展示了第 i 架无人机运行的框架的概览。第一阶段是初始化（第 III-C 节），包括检测和临时跟踪潜在的队友无人机（第 III-C.1 节）。一旦临时跟踪物体的运动足够激发，就开始轨迹匹配（第 III-C.2 节）。如果临时跟踪物体的轨迹成功匹配通过无线通信传输的队友轨迹，该物体将被视为相应队友的观测，并被标记为队友身份（ID），临时跟踪器因此成为队友跟踪器（第 III-D.1 节）。观察到的队友 $j$ 的位置 ${\mathbf{b}}_i{\breve{p}}_{b_j}$（“主动观测测量”），队友 $j$ 观察到的自我位置 ${}^{b_j}{\breve{p}}_{b_i}$（“被动观测测量”，从网络接收），激光雷达点云（运动补偿后），以及 IMU 测量值然后通过误差状态迭代卡尔曼滤波器（ESIKF）（第 III-D 节）融合，以联合估计自我状态和全局外参变换 $G_i{T}_{G_j}$。最后，估计的自我状态和主动相互观测信息通过 Ad-Hoc 通信的 UDP 数据包传输给其他无人机。

C. 群体系统的初始化

本节介绍无人机如何检测、跟踪和识别潜在的队友无人机。

1. 无人机检测和临时跟踪：我们提出了一种基于反射率过滤和聚类提取的新型无人机检测方法。对于每架无人机，其机体上附加了反光带，因此可以根据激光雷达传感器测量的反射率信息被其他队友轻松检测。算法 1 总结了无人机 i 在每次激光雷达扫描中进行的详细检测和跟踪程序。将 ${}^{b_i}{\mathcal{P}}_{\text{all}}$ 表示为当前机体框架中表示的新扫描的原始激光雷达点。首先，通过反射率过滤 ${}^{b_i}{\mathcal{P}}_{\text{all}}$ 在第 1 行提取超过给定阈值的高反射率值点，该阈值可以事先在反光带上校准。然后在第 2 行，通过欧几里得聚类 ${}^{b_i}{\mathcal{P}}_h$ 检测新的潜在队友无人机。

新检测到的物体随后在第 4 行由基于卡尔曼滤波器的临时跟踪器跟踪。

每个临时跟踪器 $m(m=1,2,\cdots M)$ 的状态向量 $x_m$ 包括物体位置 ${}^{G_i}{p}_m$ 和在无人机 i 的全局框架中的速度，临时跟踪器将根据恒定速度模型预测跟踪器位置 ${}^{G_i}{\hat{p}}_m$。然后，位置 ${\mathbf{G}}_i{\breve{p}}_m={\mathbf{G}}_i{T}_{b_i}{}^{b_i}{\breve{p}}_m$（其中 ${}^{b_i}{\breve{p}}_m$ 是在第 2 行从高反射率点聚类得到的）与最近预测位置关联。如果没有找到有效的关联，即预测位置和聚类位置的误差太大，跟踪器将在预测位置 ${}^{G_i}{\hat{p}}_m$ 周围的原始点重新聚类。原因是测量点的反射率值通常受到物体距离和激光入射角的影响，因此提取的高反射率点可能不代表潜在队友无人机上的所有点。为了获得更准确的聚类，我们计算以 ${}^{G_i}{\hat{p}}_m$ 为中心的预测区域，并在此区域内聚类物体，然后用于更新临时跟踪器。注意，提取的物体大小远大于或小于实际无人机大小的物体被拒绝（无效物体）。如果没有有效的物体可以聚类，跟踪器将传播到下一步。如果跟踪器在没有更新的情况下传播了太多步骤，跟踪器将被终止。请注意，由于预测区域内的点远少于所有输入点，因此重新聚类的时间消耗将显著减少。

2. 使用轨迹匹配进行队友识别：通过拒绝无效聚类和跟踪真正的潜在队友，每个临时跟踪器的轨迹被累积以进行后续识别。由于所提出的群体系统中的所有无人机将交换它们估计的自我状态（在它们自己的全局框架中）与其他人，队友识别和全局外参可以通过轨迹匹配获得，如下所示：

$$\arg \underset{G_i{T}_{G_j}}{\min }\sum _{\kappa =1}^{\mathcal{K}}\frac{1}{2}{\Vert }^{G_i}{\bar{p}}_{m,\kappa }-{}^{G_i}{T}_{G_j}{}^{G_j}{\breve{p}}_{b_j,\kappa }\Vert (1)$$

其中 ${\mathbf{G}}_i{\overline{p}}_{m,\kappa }\in {\mathbf{G}}_i{\mathcal{T}}_m$ 表示 m 个物体跟踪位置轨迹 ${}^{G_i}{\mathcal{T}}_m$ 中的第 $\kappa$ 个位置，${\mathbf{G}}_j{\breve{p}}_{b_j,\kappa }\in {\mathbf{G}}_j{\mathcal{T}}_j$ 表示从无人机 j 接收的位置。考虑到可能的短期通信中断，${\mathbf{G}}_j{\breve{p}}_{b_j}$ 的一些数据可能会丢失。因此，我们只选择与 ${\mathbf{G}}_j{p}_{b_j,\kappa }$ 时间戳接近的 ${\mathbf{G}}_i{\overline{p}}_{m,\kappa }$ 参与轨迹匹配。

由于数据量太大，我们使用最近 $\mathcal{K}$ 个位置的滑动窗口进行匹配。

由于如果涉及的轨迹是直线，则无法从 (1) 确定唯一的变换[28]，因此通过 TrajExcited $({}^{G_i}{\mathcal{T}}_m)$ 在第 6 行不断评估这些被跟踪物体的轨迹，直到收集到足够的信息。设 ${}^{G_i}{\overline{p}}_m^c$ 表示 ${}^{G_i}{\mathcal{T}}_m$ 的质心，TrajExcited $({}^{G_i}{\mathcal{T}}_m)$ 通过计算矩阵 $\mathcal{H}\in {\mathbb{R}}^{3\times 3}$ 的奇异值来评估 ${}^{G_i}{\mathcal{T}}_m$ 的激发（形状）：

$$\mathcal{H}\triangleq \sum _{\kappa =1}^{\mathcal{K}}\left({}^{G_i}{\overline{p}}_{m,\kappa }-{}^{G_i}{\overline{p}}_m^c\right)\cdot {\left({}^{G_i}{\overline{p}}_{m,\kappa }-{}^{G_i}{\overline{p}}_m^c\right)}^T(2)$$

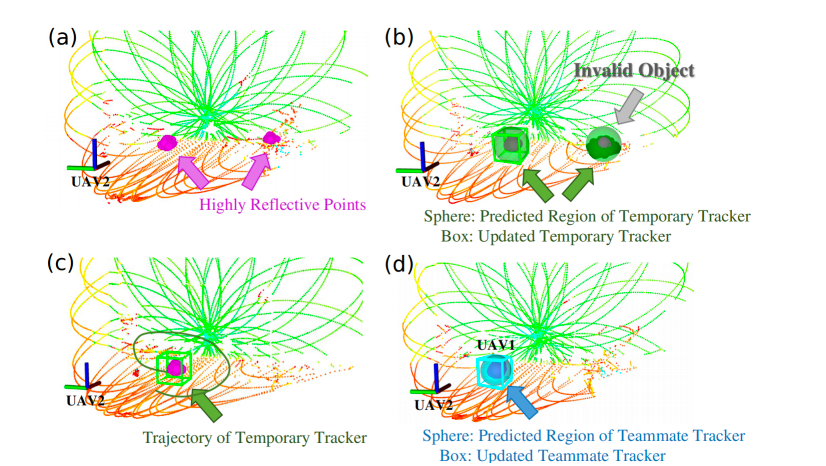
如果第二大的奇异值大于给定的阈值，则轨迹完全激发，有资格进行 TrajMatching $({}^{G_j}{\mathcal{T}}_j,{}^{G_i}{\mathcal{T}}_m)$ 在第 8 行。这个函数解决 (1) 有研究充分的闭式解法[28]。匹配是与每个接收到的队友无人机的轨迹进行的，直到匹配误差小于给定的阈值，表明物体 m 本质上是队友 j 的观测，而 (1) 的解给出了全局外参 ${}^{G_i}{T}_{G_j}$ 的初始估计，然后使用第 III-D.3 节中的 ESIKF 在线细化。识别后，临时跟踪器变为具有相应无人机 ID 的队友跟踪器，将按第 III-D.1 节顺序跟踪。初始化流程如图 3 所示。

D. 去中心化激光雷达-惯性状态估计

所提出的群体系统的完全去中心化状态估计是一个紧密耦合的迭代卡尔曼滤波器，继承自 FAST-LIO2[4]，但进一步纳入了相互观测约束以提高自我状态估计的准确性，并包括在线细化无人机间全局外参变换。
1）队友跟踪：在检测和识别队友无人机后，获得队友跟踪器，并通过轨迹匹配进行初始校准全局外参。队友跟踪器与临时跟踪器类似，但有两个关键区别。第一个区别在于预测。临时和队友跟踪器都使用恒定速度模型预测状态，但队友跟踪器基于从相应队友接收到的速度（和相应全局外参变换的最新估计）进行预测，而不是临时跟踪器中的自我估计速度（见第 III-C.1 节）。第二个区别在于没有队友观测时的状态更新。在临时跟踪器中，如果没有有效的观测，例如队友在 FoV 之外，跟踪器将传播几步然后终止，如第 III-C.1 节所述。在队友跟踪器中，它将使用从网络接收到的队友里程计，在将其转换为自我无人机的全局框架中使用第 III-D.3 节获得的最新全局外参变换后，继续状态更新。

2） 状态预测：用 $\tau$ 表示 IMU 测量索引，离散状态转移模型如下所示：

$$x_{i,\tau +1}=x_{i,\tau }⊞\left(\Delta t_{\tau }{f}_i\left(x_{i,\tau },u_{i,\tau },w_{i,\tau }\right)\right)(3)$$

$\Delta t_{\tau }$ 是两个连续 IMU 测量之间的时间间隔，$x_{i,\tau }$ 表示在 IMU 测量的时间戳 $t_{i\tau }$ 的真实状态。状态向量 $x_i$，离散状态转移函数 $f_i$，噪声 $w_i$ 和输入 $u_i$ 定义如下：

$$\begin{array}{rl}& x_i\triangleq \left[\begin{array}{lllcc}{G}_i{R}_{b_i}& G_i{p}_{b_i}& G_i{v}_{b_i}{b}_{g_i}{b}_{a_i}& G_{i}g& \\ & \dots & G_i{R}_{G_j}& G_i{p}_{G_j}& \dots \end{array}\right]\in \mathcal{M}\\ & f_i\triangleq [{\omega }_{m_i}-b_{g_i}-n_{g_i}{}^{G_i}{v}_{b_i}{}^{G_i}{R}_{b_i}\left(a_{m_i}-b_{a_i}-n_{a_i}\right)+{}^{G_i}g\\ & n_{b_{g_i}}{n}_{b_{a_i}}{0}_{3\times 1}\cdots n_R{n}_p\cdots )\\ & w_i\triangleq \left[n_{g_i}{n}_{a_i}{n}_{b_{g_i}}{n}_{b_{a_i}}{n}_R{n}_p\right],u_i\triangleq \left[{\omega }_{m_i}{a}_{m_i}\right]\end{array}$$

其中 ${\omega }_{m_i},a_{m_i}$ 表示无人机 i 的 IMU 测量值，状态向量 $x_i$ 中每个元素的含义在第 III-A 节中介绍，状态流形 $\mathcal{M}$ 定义在 (4) 中，其维数为 $18+6\times (N-1)$。

$$\mathcal{M}\triangleq \underset{\text{dim}=18}{\underbrace{SO(3)\times {\mathbb{R}}^{15}}}\times \underset{\text{dim}=6\times (N-1)}{\underbrace{\cdots \times SO(3)\times {\mathbb{R}}^3\times \cdots }}(4)$$

图3. 新检测物体的初始化示意图，点云根据反射率着色。这里自我无人机是UAV2，它需要在视野内检测和识别其他队友无人机。框的中心表示跟踪器的更新位置。(a) 反射率过滤。(b) 通过丢弃尺寸过大的物体进行异常值拒绝。© 跟踪真实的潜在队友并累积轨迹。(d) 在轨迹匹配后，该物体被识别为UAV1，临时跟踪器变为队友跟踪器（见第III-D.1节）。

在 (3) 中，我们使用了在 [29] 中定义的符号 $⊞/\boxminus$ 来紧凑地表示状态流形上的“加法”。具体来说，对于 (III-D.2) 中的状态流形 $SO(3)\times {\mathbb{R}}^n$，$⊞$ 操作及其逆操作 $\boxminus$ 定义如下：

$$\left[\begin{array}{l}R\\ a\end{array}\right]⊞\left[\begin{array}{l}r\\ b\end{array}\right]=\left[\begin{array}{c}RExp(r)\\ a+b\end{array}\right];\left[\begin{array}{l}{R}_1\\ a\end{array}\right]\boxminus \left[\begin{array}{l}{R}_2\\ b\end{array}\right]=\left[\begin{array}{c}\log \left(R_2^T{R}_1\right)\\ a-b\end{array}\right]$$

其中 $R,R_1,R_2\in SO(3),r\in {\mathbb{R}}^3,a,b\in {\mathbb{R}}^n,\mathrm{Exp}(\cdot ):{\mathbb{R}}^3\mapsto SO(3)$ 是 $SO(3)$ 上的指数映射 [29]，$\log (\cdot ):SO(3)\mapsto {\mathbb{R}}^3$ 是其逆对数映射。

在 ESIKF 框架下，第 i 架无人机的状态预测步骤在接收到新的 IMU 测量后执行如下：

$${\hat{x}}_{i,\tau +1}={\hat{x}}_{i,\tau }⊞\left(\Delta t_{\tau }{f}_i\left({\hat{x}}_{i,\tau },u_{i,\tau },0\right)\right);{\hat{x}}_0={\bar{x}}_{i,k-1}(5)$$
3) 误差状态迭代状态更新：更新步骤在新的激光雷达扫描结束时间 $t_{ik}$ 迭代执行，融合点云测量和相互观测测量（如果有）。一旦接收到新的扫描，将执行运动补偿以获得未失真的点，并将计算点到平面的距离以生成点云残差。运动补偿的细节可以参考 [4]。将每个运动未失真的点投影到全局框架中，使用传播的自我状态表示为 ${}^{G_i}{\hat{p}}_n$，将 $u_n$ 表示为相应平面的法向量，该平面上有一个点 ${}^{G_i}{q}_n$，点残差表示为 $z_{p,n}$。

除了点云残差，本文的一个主要贡献是基于 3D 激光雷达的相互观测测量，这些测量用于构建新的约束以提高状态估计的准确性，并使群体系统对退化场景具有鲁棒性。对于无人机 i，将 ${}^{b_i}{\breve{p}}_{b_j}$（相对于无人机 j 的主动观测测量，见第 III-D.1 节）产生的主动观测残差表示为 $z_{ao,ij}$，将 ${}^{b_j}{\breve{p}}_{b_i}$（相对于无人机 j 的被动观测测量）产生的被动观测残差表示为 $z_{po,ij}$，那么无人机 i 的残差块组成如下：

$$\begin{array}{rl}{z}_i& ={\left[\cdots ,z_{p,n}^T,\cdots ,z_{ao,ij}^T,\cdots ,z_{po,ij}^T,\cdots \right]}^T\\ z_{p,n}& =u_n^T\left({}^{G_i}{\hat{p}}_n-{}^{G_i}{q}_n\right)\\ z_{ao,ij}& ={}^{G_i}{T}_{b_i}^{-1G_i}{T}_{G_j}{}^{G_j}{\breve{p}}_{b_j}-{}^{b_i}{\breve{p}}_{b_j}\\ z_{po,ij}& ={}^{G_j}{\check{T}}_{b_j}^{-1G_i}{T}_{G_j}^{-1G_i}{p}_{b_i}-{}^{b_j}{\breve{p}}_{b_i}\end{array}(6)$$

状态将迭代更新直至收敛，细节可以参考 [4]。收敛后，地图将使用 ikd-tree [30] 进行增量更新，这是一种高效的地图管理数据结构。通过使用更新的全局外参变换投影队友无人机传输的自我状态信息来完成相对状态估计。

四. 实验

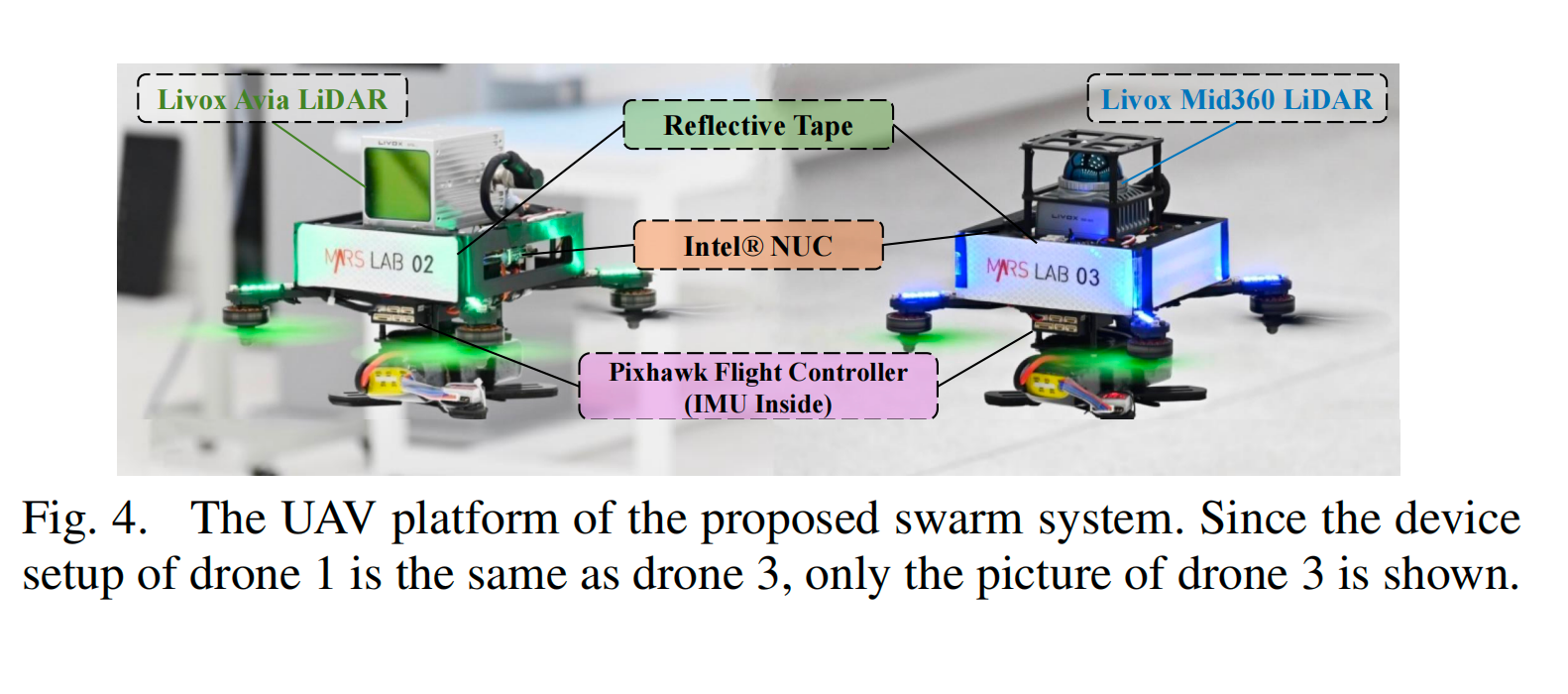
实验平台包含三架无人机，每架无人机携带一个 Livox 激光雷达（无人机 1 和无人机 3 携带 Livox Mid360，无人机 2 携带 Livox Avia，具有较小的 FoV），一个 Pixhawk 飞行控制器（内置 BMI055 6 轴 IMU），一个英特尔 NUC 笔记本电脑，配备 i7-10710U CPU。每架无人机都附有反光带以便易于检测（见图 4）。对于每架无人机，激光雷达和 IMU 之间的时间偏移和外参通过 [31] 校准，不同无人机之间的时间事先基于网络时间协议（NTP）同步。所有无人机都使用模型预测控制 [11] 手动飞行。

图 4. 所提出的群体系统的无人机平台。由于无人机 1 的设备设置与无人机 3 相同，仅显示了无人机 3 的图片。

A. 室内飞行

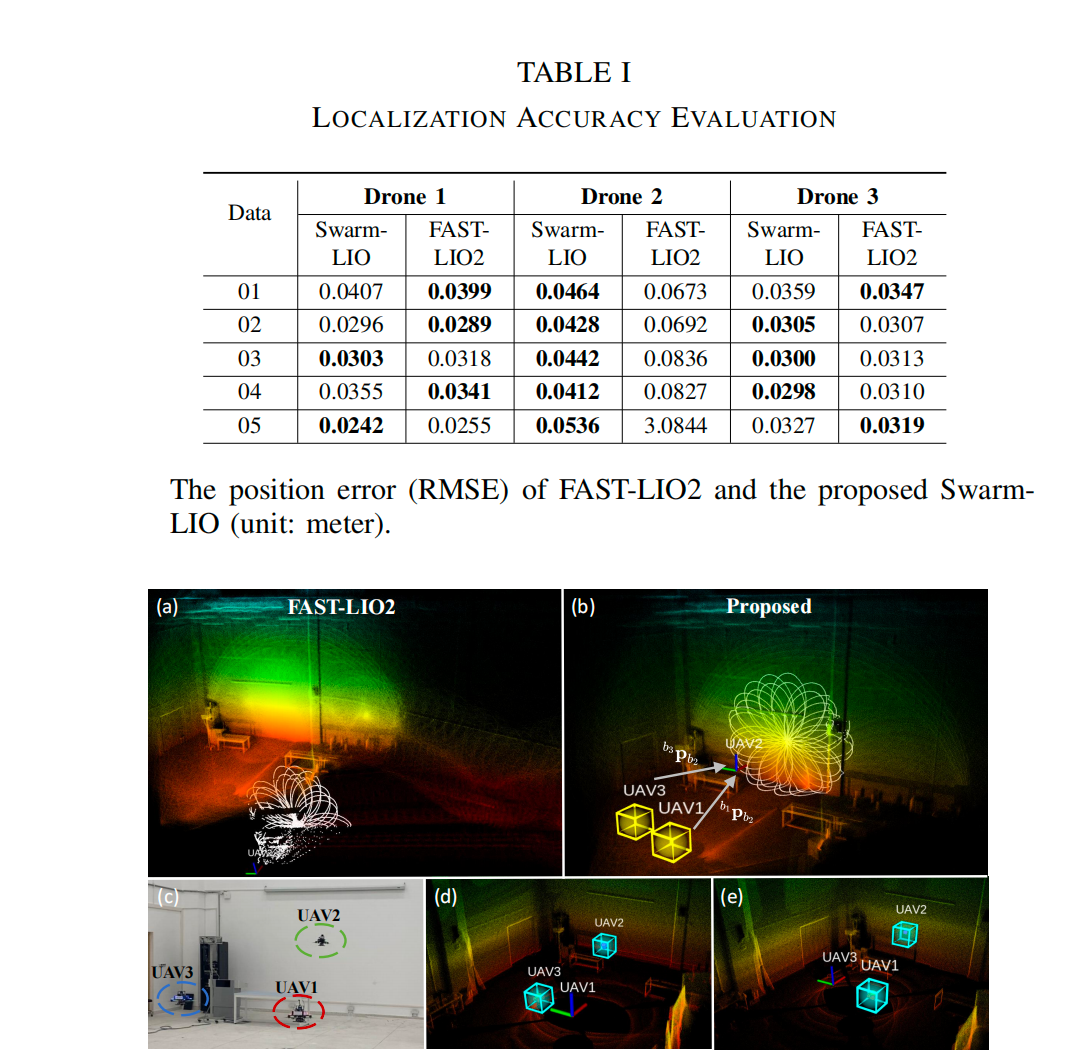
在室内场景中进行了五次飞行，以定位精度。运动捕捉系统作为真实数据。就我们所知，对于基于 3D 激光雷达的状态估计系统，我们进行了消融研究，将我们方法的定位精度与 FAST-LIO2 进行比较，表中显示了位置 RMSE。对于携带 Livox Avia 激光雷达的无人机 2，由于其 $70.4^{\circ }$ 的 FoV 使得激光雷达更容易丢失特征，尤其是在室内场景中，观测测量可以提供准确的定位结果。对于携带 $360^{\circ }$ 激光雷达的无人机 3，有足够的点使 FAST-LIO2 工作良好。因此，在所有实验中，激光雷达的时间间隔是 L，该方法和 FAST-LIO2 的平均每次迭代时间消耗为 $17.5ms$，所提出的 Swarm-LIO 可以提高实时性，并且具有近似的计算效率（单架无人机的快速里程计）。

B. 退化环境飞行

第一个退化场景是表 I 中的数据 05，其中携带 Livox Avia 激光雷达的无人机 2 面对一个平滑的墙壁，这导致不足以确定完整状态的约束。结果，单智能体里程计 FAST-LIO2 完全退化，RMSE 很大。而对于所提出的群体系统，无人机 2 被其队友无人机 1 和无人机 3 观测（被动观测测量）。在 (6) 中融合从无人机 1 和无人机 3 传输的被动观测测量仍然可以导致稳定且准确的状态估计。点云地图和相互观测测量如图 5 所示。

第二个退化场景是一个平滑的立方体走廊。与平滑墙面相似，单个LiDAR的观测无法提供足够的约束来确定姿态，因此FAST-LIO2会出现漂移。而对于一个群体系统，当第一架无人机飞入走廊时，其他无人机仍然在入口处悬停（该处有足够的结构特征供其状态估计）并为第一架无人机提供被动观测测量。在第一架无人机穿过走廊后，它在尽头悬停，为其余无人机提供被动观测测量，使它们也能飞过走廊。因此，整个群体可以顺利穿过平滑走廊而不出现退化。从图6可以看出，所提出的方法对这种类型的退化场景具有鲁棒性，地图能够恢复比FAST-LIO2更多的结构细节。更多的视觉说明可以在我们的视频中找到。

图5. 退化平滑墙实验。图(a)和图(b)中的白点指当前输入点。(a) 无人机2的视图，采用FAST-LIO2构建的点云地图，出现严重漂移，地图混乱。(b) 无人机2的视图，采用所提出的方法融合被动观测测量b1与b2以及b3与b2构建的点云地图。黄色框表示队友无人机超出了视野，队友跟踪器通过融合队友传输的自我状态估计进行更新。© 三架无人机的图片。(d)(e) 无人机1和无人机3的视图及其对队友无人机的观测（蓝框）。

C. 去中心化部署

为了验证所提出的群体系统对观测丢失的鲁棒性以及全球外部变换的校准能力，进行了一项大规模去中心化探索实验。三架无人机随机放置在一座豪宅前，然后起飞。起飞后，它们进行了一些随机飞行，每架无人机自动检测、跟踪和识别彼此，无需任何先前的外部信息。之后，无人机向不同方向飞行，以探索不同区域。飞行结束后，每架无人机的点云地图可以使用估计的全球外部变换在离线状态下合并在一起。通过将无人机2和无人机3的点云地图转换到无人机1的全球坐标系中，合并的地图如图7所示。
一致的合并地图展示了在没有任何初始值的情况下准确进行全球外部估计的能力。另一个需要注意的点是，由于无人机在不同区域飞行，长时间内没有相互观测，例如，无人机2在没有相互观测的情况下的平均距离为88.58米。但即便如此，当队友无人机返回到无人机2的视野时，检测到的队友位置与队友跟踪器预测的位置（基于接收到的队友自我状态，见第III-D.1节）之间的误差仅为0.17米，这表明估计的全球外部变换具有很高的准确性。更多的视觉说明可在我们的视频中查看。

五. 结论和未来工作

本文提出了一种完全去中心化且准确的群体激光雷达-惯性里程计。提出了一种新颖的基于3D激光雷达的无人机检测、识别和跟踪方法，以执行完全自主的初始化和鲁棒的相对状态估计。在ESIKF框架下，相互观测测量与IMU和点云测量紧密结合，实现了实时且准确的自我状态估计，即使在相机或激光雷达的退化环境中也能保持鲁棒性。未来，无人机检测可以升级为无需辅助的方法（例如，无需反光带），并且初始化可以更加高效。此外，群体的规模可以更大，将生产更多的无人机以完成各种任务。