资源和文章同步更新至微信公众号:算法工程师之路
今天我们来聊一聊图结构,虽然在面试中图结构用的不多,但是我真的觉得图结构可以综合很多知识点,以及STL中容器的使用,并且需要很强大的逻辑性!是一个锻炼脑子的东西,并且Coding起来非常之爽~~
图的建立
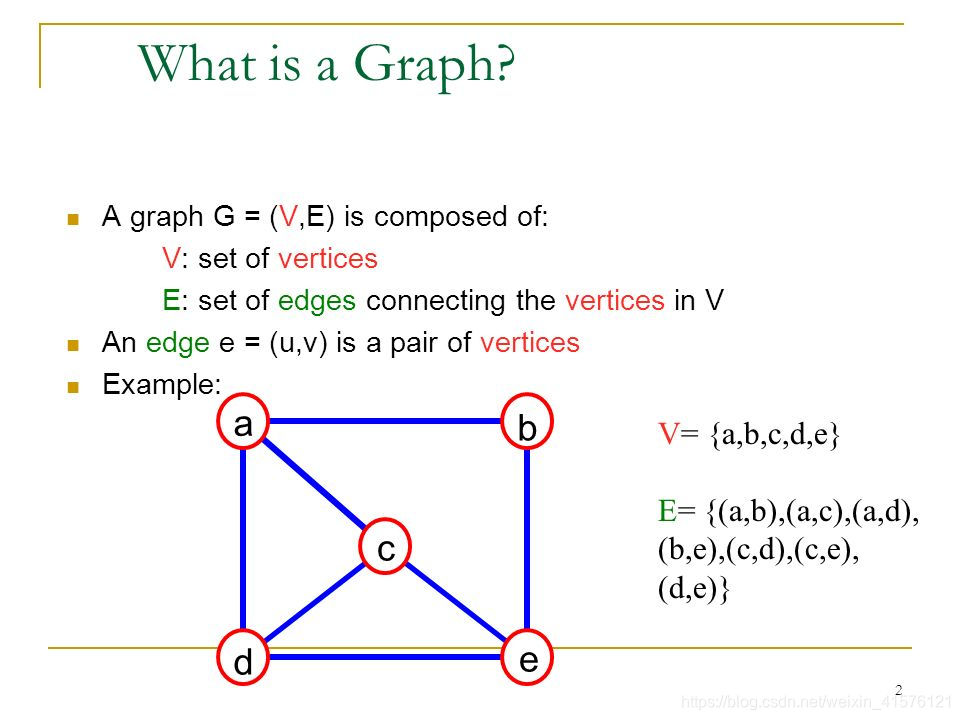
我们使用算法来模拟图结构之前,需要首先搞清楚图结构都需要什么元素!一般来说我们将一张图定义为G=(V, E),其中集合V表示顶点(nodes),而集合E表示某一对顶点之间的关系,叫做边,如果这种关系是单向的,那么形成的图为有向图,反之如果是双向的,那么形成的图就是无向图,如果一个图中顶点的关系既有单向,又存在双向,那么叫做混合图!
顶点类
对于一个顶点而言,我们需要定义什么呢?主要有以下几个属性:
- 顶点的值value
- 顶点的入度in(也就是指向该顶点的边数)
- 顶点的出度out(也就是从该顶点出发的边数)
- to节点的集合nexts(有向图时,指向的节点为to节点,当前节点为from节点)
- 从该节点出发边的集合edges
然后顶点的类定义如下:
使用list的原因是因为list相比vector在中间操作数据更加快速!
class Node{
public:
int value;
int in;
int out;
list<Node*> nexts; // 当前节点为from,to的节点的集合
list<Edge*> edges;
Node(int value){
this->value = value;
in = 0;
out = 0;
}
};
边类
对于边的定义就很简单了,确定一个边只要知道其从哪个顶点来,到那个顶点去就好了,还有如果是带权图,每个边都有一个权重属性!因此对于边类来说,其属性很简单,如下:
- 权重weight
- from节点
- to节点
边类的定义如下:
class Edge{
public:
int weight;
Node* from;
Node* to;
Edge(int weight, Node* from, Node* to){
this->weight = weight;
this->from = from;
this->to = to;
}
};
图类
由于上面也说了,一张图其实质就是一个点的集合+一个边的集合,并且这些元素都是无序的,因此为了更加便捷的访问,所以我们在这里都是用基于哈希函数的无序容器结构来储存!
注意:如果使用自定义类型,需要重写哈希函数,请参考原来的文章:
如何使用哈希容器来操作自定义类型
图类的定义如下:
class Graph{
public:
unordered_map<int, Node*> nodes;
unordered_set<Edge*> edges;
};
当我们准备好了这些类之后,我们就可以建立整个图了,我们使用邻接矩阵的形式,只需要输入一个边的权重、from节点的值和to节点的值就可以创建两个节点和一条边,然后添加入整个图中!
建立过程中,一定要注意,当加入一条边时,我们一定要将from节点的出度+1,to节点的入度+1,然后将to节点添加到from节点的nexts中,并将这个边添加到from节点的边集edges。
class GraphGenerator{
// 三列分别是权重,from, to
public:
Graph createGraph(vector<vector<int>> matrix, int rows, int cols){
Graph graph;
for(int i=0;i < rows;i ++){
int weight = matrix[i][0];
int from = matrix[i][1];
int to = matrix[i][2];
if(graph.nodes.find(from) == graph.nodes.end()){
graph.nodes[from] = new Node(from);
}
if(graph.nodes.find(to) == graph.nodes.end()){
graph.nodes[to] = new Node(to);
}
Node* fromNode = graph.nodes.find(from)->second;
Node* toNode = graph.nodes.find(to)->second;
Edge* newEdge = new Edge(weight, fromNode, toNode);
// 新增一条边,则to节点的入度增加
toNode->in++;
// from节点的出度增加
fromNode->out++;
fromNode->nexts.push_back(toNode);
fromNode->edges.push_back(newEdge);
graph.edges.insert(newEdge);
}
return graph;
}
};
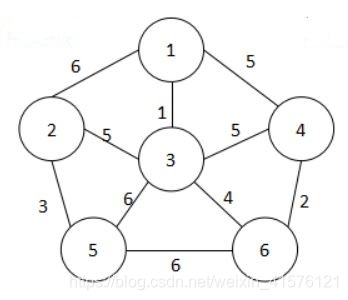
那么我们如何创建一个有向图和无向图呢?由于我们的edge是有指向的,从from节点到to节点,假设有向图的边为1->3,那么我们可以用有向图的方式创建无向图,只不过多了一个描述,则为1->3, 3->1。例如下面这个无向图,我们可以这样创建:
vector<vector<int>> matrix = {{6, 1, 2}, {5, 1, 4}, {2, 6, 4},
{6, 6, 5}, {3, 2, 5}, {1, 3, 1},
{5, 3, 2}, {6, 3, 5}, {4, 3, 6}, {5, 3, 4},
// 只到这里为一个有向图,from和to再反过来一遍就是无向的了
{6, 2, 1}, {5, 4, 1}, {2, 4, 6},
{6, 5, 6}, {3, 5, 2}, {1, 1, 3},
{5, 2, 3}, {6, 5, 3}, {4, 6, 3}, {5, 4, 3}};
BFS(广度优先遍历)
广度优先遍历算法,从一个节点开始,优先打印其所有的下一节点,然后再打印其下一节点的下一节点,这时候就需要我们标记这个节点是否被打印过,避免重复打印!因此我们使用unordered_set用来储存访问过的节点,并使用队列结构来储存将要打印的节点,接着在打印一个节点的同时要把其所有下一节点且未访问过的压入队列中!
// 广度优先遍历图节点
void bfs(Node* node){
if(node == nullptr){
return;
}
queue<Node*> que;
unordered_set<Node*> set; // 用来标示是否访问过
Node* help;
que.push(node);
set.insert(node);
while(!que.empty()){
help = que.front();
que.pop();
cout << help->value << " ";
// 使用出队的当前节点来找
for(auto node: help->nexts){
if(set.find(node) == set.end()){
que.push(node);
set.insert(node);
}
}
}
cout << endl;
}
DFS(深度优先遍历)
深度优先遍历算法同样也需要一个容器用来标记是否被访问过,但是与BFS不同的是其使用的是栈结构,原因是对于DFS来说是从一个点一直遍历到最后节点,然后还要返回到上一节点判断,如果其nexts中的节点都标记访问过了,那么就再向上回溯,如果有没有访问过的节点,那么就访问,一直重复这个过程!而栈结构可以维护我们的访问节点顺序,便于回溯!
// 深度优先遍历图节点
void dfs(Node* node){
stack<Node*> sta;
unordered_set<Node*> set; // 用来标示是否被访问过
Node* help; // 辅助节点
// 入栈的同时并打印信息
sta.push(node);
set.insert(node);
cout << node->value << " ";
while(!sta.empty()){
help = sta.top();
sta.pop();
// 对出栈的元素判断,如果被打印过,则不会被压栈,说明访问过了
for(auto node: help->nexts){
if(set.find(node) == set.end()){
cout << node->value << " ";
sta.push(help); // 将访问的节点入栈,由于当前节点可能还有的分支没有访问
sta.push(node);
set.insert(node);
break; // 每次只访问某个节点的一个分支,一直深入下去访问
}
}
}
cout << endl;
}
资源分享
以上完整代码文件(C++版),文件名为:图的创建和遍历,请关注我的个人公众号 (算法工程师之路),回复"左神算法基础CPP"即可获得,并实时更新!希望大家多多支持哦~
公众号简介:分享算法工程师必备技能,谈谈那些有深度有意思的算法,主要范围:C++数据结构与算法/深度学习(CV),立志成为Offer收割机!坚持分享算法题目和解题思路(Day By Day)