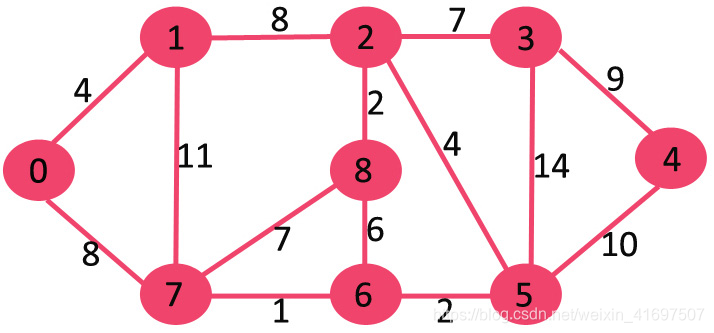
给定图中的图形和源顶点，找到给定图形中从源到所有顶点的最短路径。
Dijkstra的算法与最小生成树的Prim算法非常相似。与Prim的MST一样，我们以给定的源为根生成SPT（最短路径树）。我们维护两组，一组包含最短路径树中包含的顶点，另一组包括最短路径树中尚未包括的顶点。在算法的每个步骤中，我们找到一个顶点，该顶点位于另一个集合中（尚未包括的集合）并且与源具有最小距离。

下面是Dijkstra算法中用于查找给定图形中从单个源顶点到所有其他顶点的最短路径的详细步骤。
算法
1）创建一个集sptSet（最短路径树集），它跟踪最短路径树中包含的顶点，即，计算并最终确定与源的最小距离。最初，这个集合是空的。
2）为输入图中的所有顶点指定距离值。将所有距离值初始化为INFINITE。将源顶点的距离值指定为0，以便首先拾取它。
3）虽然sptSet不包括所有顶点
… .a）选择sptSet中不存在的顶点u并且具有最小距离值。
… .b）将你包括在sptSet中。
… .c）更新u的所有相邻顶点的距离值。要更新距离值，请遍历所有相邻顶点。对于每个相邻顶点v，如果u（来自源）和边缘u-v的权重的距离值之和小于v的距离值，则更新v的距离值。

让我们通过以下示例来理解：

set sptSet最初为空，分配给顶点的距离为{0，INF，INF，INF，IN