LeetCode 23 合并 K 个升序链表
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/merge-k-sorted-lists/description/
博主Github:https://github.com/GDUT-Rp/LeetCode
题目:
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例1:
输入:lists = [[1,4,5],[1,3,4],[2,6]]
输出:[1,1,2,3,4,4,5,6]
解释:链表数组如下:
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6
示例2:
输入:lists = []
输出:[]
示例3:
输入:lists = [[]]
输出:[]
提示:
- k == lists.length
- 0 <= k <= 1 0 4 10^4 104
- 0 <= lists[i].length <= 500
- − 1 0 4 -10^4 −104 <= lists[i][j] <= 1 0 4 10^4 104
- lists[i] 按 升序 排列
- lists[i].length 的总和不超过 10^4
解题思路:
方法一:顺序合并
用一个变量 ans 来维护以及合并的链表,第 i 次循环把第 i 个链表和 ans 合并,答案保存到 ans 中。
Golang
/**
* Definition for singly-linked list.
* type ListNode struct {
* Val int
* Next *ListNode
* }
*/
func mergeKLists(lists []*ListNode) *ListNode {
var ans *ListNode
for i:=0; i<len(lists); i++ {
ans = mergeTwoLists(ans, lists[i])
}
return ans
}
func mergeTwoLists(a *ListNode, b *ListNode) *ListNode {
if a == nil {
return b
}
if b == nil {
return a
}
var head ListNode
tail := &head
for (a != nil && b != nil) {
if a.Val < b.Val {
tail.Next = a
a = a.Next
} else {
tail.Next = b
b = b.Next
}
tail = tail.Next
}
if a != nil {
tail.Next = a
} else {
tail.Next = b
}
return head.Next
}
C++
class Solution {
public:
ListNode* mergeTwoLists(ListNode *a, ListNode *b) {
if ((!a) || (!b)) return a ? a : b;
ListNode head, *tail = &head, *aPtr = a, *bPtr = b;
while (aPtr && bPtr) {
if (aPtr->val < bPtr->val) {
tail->next = aPtr; aPtr = aPtr->next;
} else {
tail->next = bPtr; bPtr = bPtr->next;
}
tail = tail->next;
}
tail->next = (aPtr ? aPtr : bPtr);
return head.next;
}
ListNode* mergeKLists(vector<ListNode*>& lists) {
ListNode *ans = nullptr;
for (size_t i = 0; i < lists.size(); ++i) {
ans = mergeTwoLists(ans, lists[i]);
}
return ans;
}
};
Java
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
ListNode ans = null;
for (int i = 0; i < lists.length; ++i) {
ans = mergeTwoLists(ans, lists[i]);
}
return ans;
}
public ListNode mergeTwoLists(ListNode a, ListNode b) {
if (a == null || b == null) {
return a != null ? a : b;
}
ListNode head = new ListNode(0);
ListNode tail = head, aPtr = a, bPtr = b;
while (aPtr != null && bPtr != null) {
if (aPtr.val < bPtr.val) {
tail.next = aPtr;
aPtr = aPtr.next;
} else {
tail.next = bPtr;
bPtr = bPtr.next;
}
tail = tail.next;
}
tail.next = (aPtr != null ? aPtr : bPtr);
return head.next;
}
}
复杂度分析
时间复杂度: 假设每个链表的最长长度是 n。在第一次合并后,ans 的长度为 n;第二次合并后,ans 的长度为 2n,第 i 次合并后,ans 的长度为 i×n。第 i 次合并的时间代价是 O(n+(i−1)×n)=O(i×n),那么总的时间代价为 O ( ∑ i = 1 k ( i × n ) ) = O ( ( 1 + k ) ⋅ k 2 × n ) = O ( k 2 n ) O(\sum_{i = 1}^{k} (i \times n)) = O(\frac{(1 + k)\cdot k}{2} \times n) = O(k^2 n) O(∑i=1k(i×n))=O(2(1+k)⋅k×n)=O(k2n),故渐进时间复杂度为 O ( k 2 n ) O(k^2 n) O(k2n)。
空间复杂度 O(1) 。
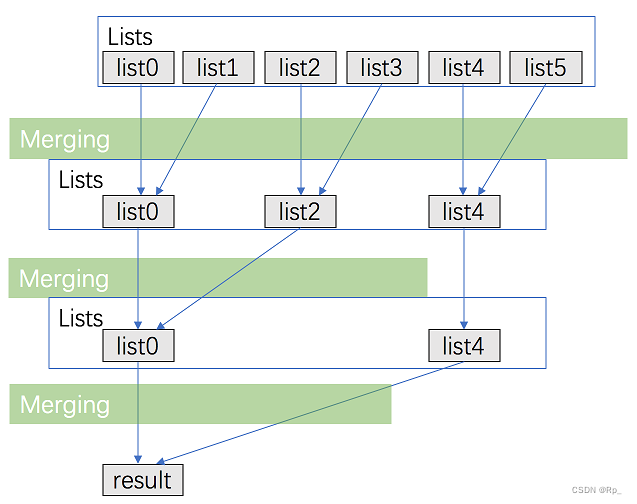
方法二:分治合并
考虑优化方法一,用分治的方法进行合并。
- 将 kkk 个链表配对并将同一对中的链表合并;
- 第一轮合并以后, k 个链表被合并成了 k 2 \frac{k}{2} 2k 个链表,平均长度为 2 n k \frac{2n}{k} k2n,然后是 k 4 \frac{k}{4} 4k 个链表, k 8 \frac{k}{8} 8k 个链表等等;
- 重复这一过程,直到我们得到了最终的有序链表。
Golang
/**
* Definition for singly-linked list.
* type ListNode struct {
* Val int
* Next *ListNode
* }
*/
func mergeKLists(lists []*ListNode) *ListNode {
return merge(lists, 0, len(lists) - 1)
}
func merge(lists []*ListNode, left, right int) *ListNode {
if left == right {
return lists[left]
}
if left > right {
return nil
}
mid := (left + right) >> 1
return mergeTwoLists(merge(lists, left, mid), merge(lists, mid+1, right))
}
func mergeTwoLists(a *ListNode, b *ListNode) *ListNode {
if a == nil {
return b
}
if b == nil {
return a
}
var head ListNode
tail := &head
for (a != nil && b != nil) {
if a.Val < b.Val {
tail.Next = a
a = a.Next
} else {
tail.Next = b
b = b.Next
}
tail = tail.Next
}
if a != nil {
tail.Next = a
} else {
tail.Next = b
}
return head.Next
}
C++
class Solution {
public:
ListNode* mergeTwoLists(ListNode *a, ListNode *b) {
if ((!a) || (!b)) return a ? a : b;
ListNode head, *tail = &head, *aPtr = a, *bPtr = b;
while (aPtr && bPtr) {
if (aPtr->val < bPtr->val) {
tail->next = aPtr; aPtr = aPtr->next;
} else {
tail->next = bPtr; bPtr = bPtr->next;
}
tail = tail->next;
}
tail->next = (aPtr ? aPtr : bPtr);
return head.next;
}
ListNode* merge(vector <ListNode*> &lists, int l, int r) {
if (l == r) return lists[l];
if (l > r) return nullptr;
int mid = (l + r) >> 1;
return mergeTwoLists(merge(lists, l, mid), merge(lists, mid + 1, r));
}
ListNode* mergeKLists(vector<ListNode*>& lists) {
return merge(lists, 0, lists.size() - 1);
}
};
Java
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
return merge(lists, 0, lists.length - 1);
}
public ListNode merge(ListNode[] lists, int l, int r) {
if (l == r) {
return lists[l];
}
if (l > r) {
return null;
}
int mid = (l + r) >> 1;
return mergeTwoLists(merge(lists, l, mid), merge(lists, mid + 1, r));
}
public ListNode mergeTwoLists(ListNode a, ListNode b) {
if (a == null || b == null) {
return a != null ? a : b;
}
ListNode head = new ListNode(0);
ListNode tail = head, aPtr = a, bPtr = b;
while (aPtr != null && bPtr != null) {
if (aPtr.val < bPtr.val) {
tail.next = aPtr;
aPtr = aPtr.next;
} else {
tail.next = bPtr;
bPtr = bPtr.next;
}
tail = tail.next;
}
tail.next = (aPtr != null ? aPtr : bPtr);
return head.next;
}
}
时间复杂度:考虑递归「向上回升」的过程——第一轮合并
k
2
\frac{k}{2}
2k 组链表,每一组的时间代价是
O
(
2
n
)
O(2n)
O(2n);第二轮合并
k
4
\frac{k}{4}
4k 组链表,每一组的时间代价是
O
(
4
n
)
O(4n)
O(4n)…所以总的时间代价是
O
(
∑
i
=
1
∞
k
2
i
×
2
i
n
)
=
O
(
k
n
×
log
k
)
O(\sum_{i = 1}^{\infty} \frac{k}{2^i} \times 2^i n) = O(kn \times \log k)
O(∑i=1∞2ik×2in)=O(kn×logk),故渐进时间复杂度为
O
(
k
n
×
log
k
)
O(kn \times \log k)
O(kn×logk)
空间复杂度:递归会使用到
O
(
log
k
)
O(\log k)
O(logk) 空间代价的栈空间。
方法三:使用优先队列/最小堆合并
这个方法和前两种方法的思路有所不同
我们需要维护当前每个链表没有被合并的元素的最前面一个, k k k 个链表就最多有 k k k 个满足这样条件的元素,每次在这些元素里面选取 val 属性最小的元素合并到答案中。
在选取最小元素的时候,我们可以用优先队列/最小堆来优化这个过程。
Golang
/**
* Definition for singly-linked list.
* type ListNode struct {
* Val int
* Next *ListNode
* }
*/
import "container/heap"
type Status struct {
Val int
Ptr *ListNode
}
type PriorityQueue []*Status
func (pq PriorityQueue) Len() int {
return len(pq)
}
func (pq PriorityQueue) Less(i, j int) bool {
return pq[i].Val < pq[j].Val
}
func (pq PriorityQueue) Swap(i, j int) {
pq[i], pq[j] = pq[j], pq[i]
}
func (pq *PriorityQueue) Push(x interface{}) {
*pq = append(*pq, x.(*Status))
}
func (pq *PriorityQueue) Pop() interface{} {
old := *pq
n := len(old)
item := old[n-1]
old[n-1] = nil
*pq = old[0 : n-1]
return item
}
func mergeKLists(lists []*ListNode) *ListNode {
var q PriorityQueue
heap.Init(&q)
for _, node := range lists {
// 每个链表第一个都放进这个堆
if node != nil {
heap.Push(&q, &Status{Val: node.Val, Ptr: node})
}
}
var head ListNode
tail := &head
for q.Len() > 0 {
// 取出最小的
f := heap.Pop(&q).(*Status)
tail.Next = f.Ptr
tail = tail.Next
// 只要所取的节点后面还要数据
if f.Ptr.Next != nil {
// 就放进堆里来
heap.Push(&q, &Status{Val: f.Ptr.Next.Val, Ptr: f.Ptr.Next})
}
}
return head.Next
}
Java
class Solution {
class Status implements Comparable<Status> {
int val;
ListNode ptr;
Status(int val, ListNode ptr) {
this.val = val;
this.ptr = ptr;
}
public int compareTo(Status status2) {
return this.val - status2.val;
}
}
PriorityQueue<Status> queue = new PriorityQueue<Status>();
public ListNode mergeKLists(ListNode[] lists) {
for (ListNode node: lists) {
if (node != null) {
queue.offer(new Status(node.val, node));
}
}
ListNode head = new ListNode(0);
ListNode tail = head;
while (!queue.isEmpty()) {
Status f = queue.poll();
tail.next = f.ptr;
tail = tail.next;
if (f.ptr.next != null) {
queue.offer(new Status(f.ptr.next.val, f.ptr.next));
}
}
return head.next;
}
}
C++
class Solution {
public:
struct Status {
int val;
ListNode *ptr;
bool operator < (const Status &rhs) const {
return val > rhs.val;
}
};
priority_queue <Status> q;
ListNode* mergeKLists(vector<ListNode*>& lists) {
for (auto node: lists) {
if (node) q.push({node->val, node});
}
ListNode head, *tail = &head;
while (!q.empty()) {
auto f = q.top(); q.pop();
tail->next = f.ptr;
tail = tail->next;
if (f.ptr->next) q.push({f.ptr->next->val, f.ptr->next});
}
return head.next;
}
};
复杂度分析
时间复杂度:考虑优先队列中的元素不超过
k
k
k 个,那么插入和删除的时间代价为 ¥O(\log k)$,这里最多有
k
n
kn
kn 个点,对于每个点都被插入删除各一次,故总的时间代价即渐进时间复杂度为
O
(
k
n
×
log
k
)
O(kn \times \log k)
O(kn×logk)。
空间复杂度:这里用了优先队列,优先队列中的元素不超过
k
k
k 个,故渐进空间复杂度为
O
(
k
)
O(k)
O(k)。