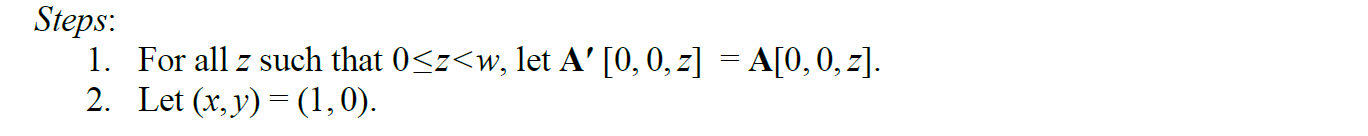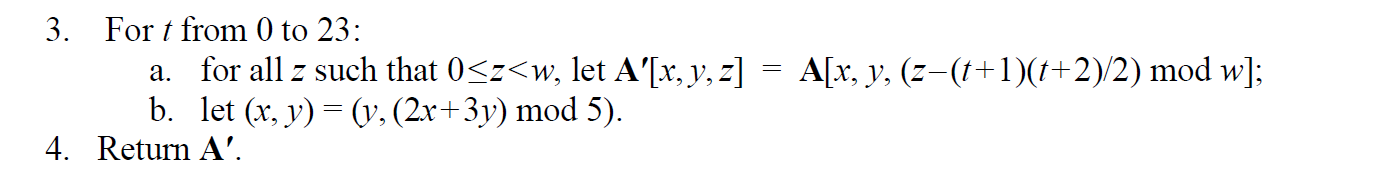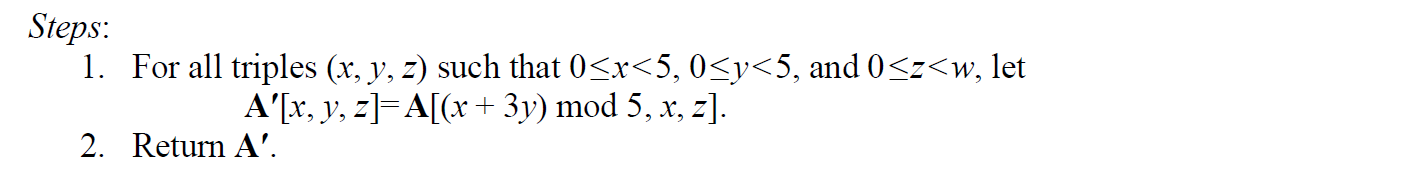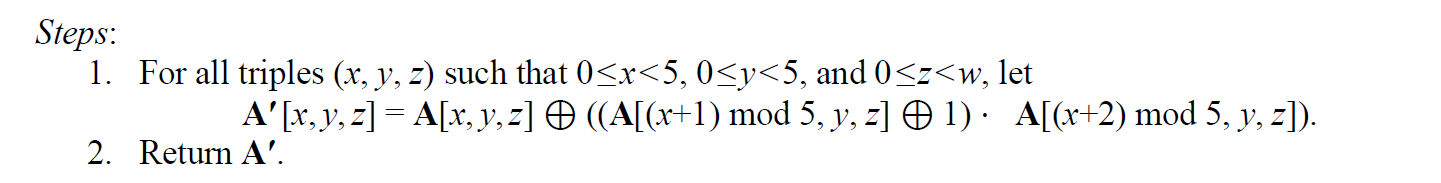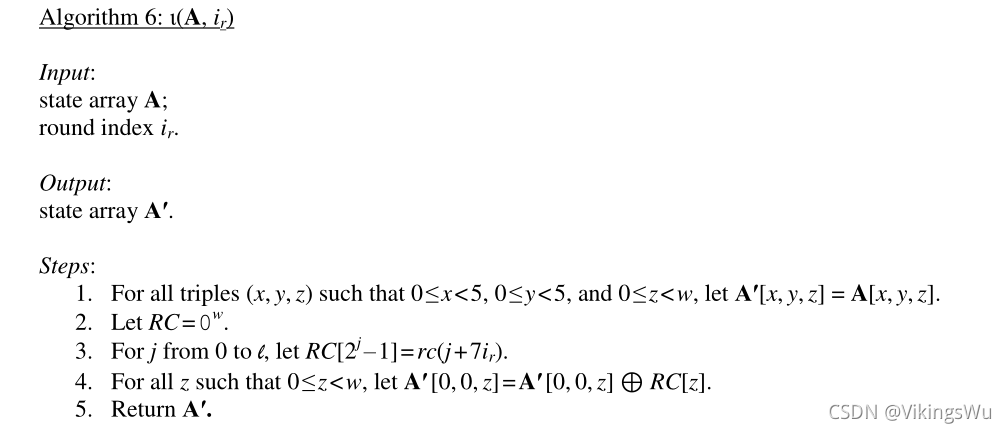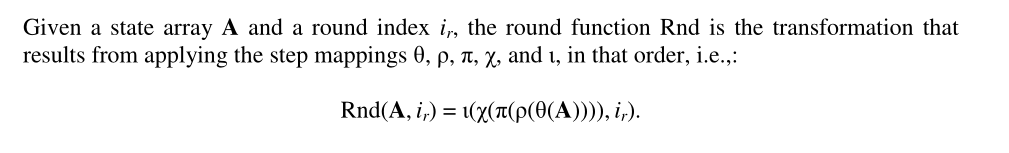SHA-3算法的计算过程详解
主要参考文档 SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions
1. 几个重要参数:
- 存储状态 S S S的比特位宽为 b b b,其中 b ∈ 25 , 50 , 100 , 200 , 400 , 800 , 1600 b∈{25,50,100,200,400,800,1600} b∈25,50,100,200,400,800,1600,可以写作 b = 25 × 2 l , l ∈ { 0 , 1 , ⋯ , 6 } b=25×2^l,l∈\left\{0,1,⋯ ,6\right\} b=25×2l,l∈{0,1,⋯,6};
- 存储状态 S S S可以分为比特率和容量两部分,其比特位宽分别为 r r r和 c c c,很明显 b = r + c b=r+c b=r+c;
2. 计算过程:
1. 填充:
在消息
M
M
M后加入
1
1
1、最少个数的
0
0
0和
1
1
1,即:
100
⋯
001
100⋯001
100⋯001,使填充后的消息长度是
r
(
0
≤
r
≤
b
)
r(0≤r≤b)
r(0≤r≤b)的整数倍。加入的比特长度至少是
2
2
2比特,最多是
r
+
1
r+1
r+1比特。
记填充后的消息为
P
P
P,
n
=
l
e
n
(
P
)
/
r
n=len(P)/r
n=len(P)/r。即将
P
P
P分成
n
n
n段,记为
P
=
P
0
∣
∣
P
2
∣
∣
⋯
∣
∣
P
n
−
1
∣
∣
P
n
P=P_0||P_2||\cdots ||P_{n-1}||P_{n}
P=P0∣∣P2∣∣⋯∣∣Pn−1∣∣Pn,每段长度为
r
r
r。
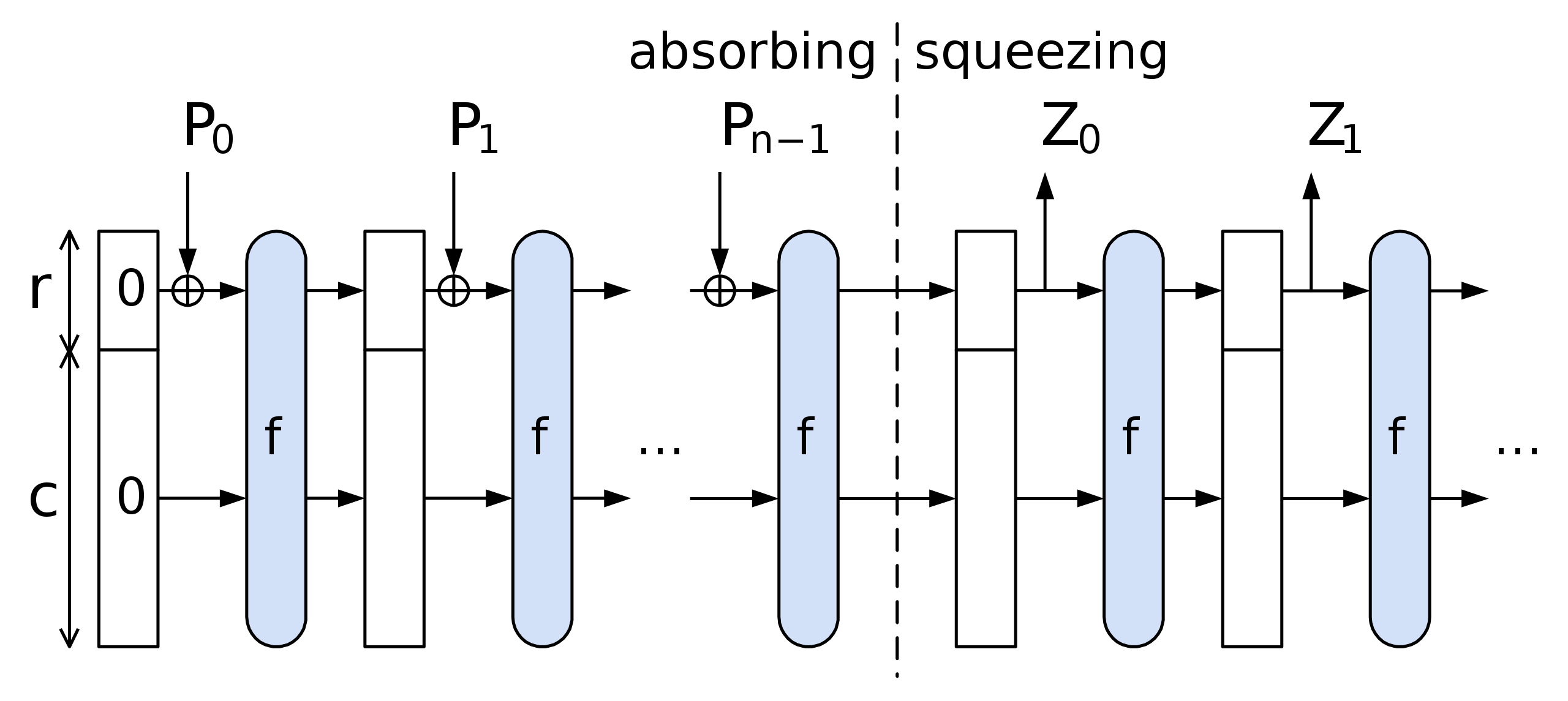
2. 吸收阶段:
S
i
+
1
=
f
(
S
i
⊕
(
P
i
∣
∣
0
c
)
)
S_{i+1}=f(S_{i}⊕(Pi ∣∣0^c ))
Si+1=f(Si⊕(Pi∣∣0c))
在吸收阶段,首先将
S
S
S初始化为零,记初始状态为
S
0
S_{0}
S0。
每一轮运算中先将
P
i
P_i
Pi后填充长度为
c
c
c的
0
0
0,再与长度为
b
b
b的
S
i
S_i
Si的进行异或运算,其结果
S
i
′
S_i^{'}
Si′经过
f
f
f函数后作为下一轮的新状态
S
i
+
1
S_{i+1}
Si+1,这过程一直重复到所有的输入都用完为止,即进行
n
n
n轮这样的运算。
在介绍
f
f
f函数之前,先要介绍一种存储结构的转换
S
i
′
→
A
S_i^{'}→A
Si′→A:
S
i
′
S_i^{'}
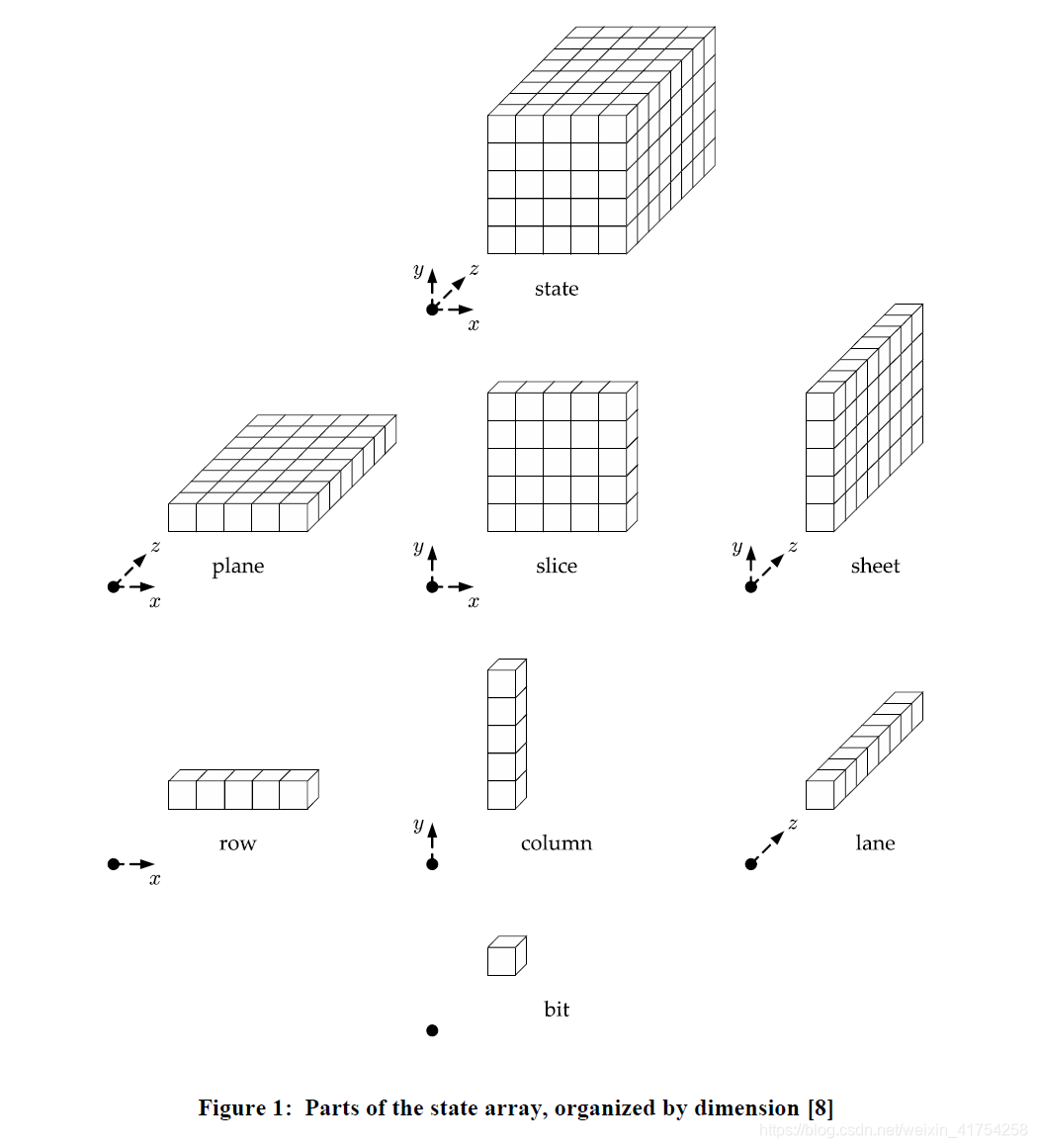
Si′是比特串,而状态
A
A
A可以表示为一个
5
×
5
×
w
5×5×w
5×5×w的三维数组,其中
w
=
b
/
25
w=b/25
w=b/25。
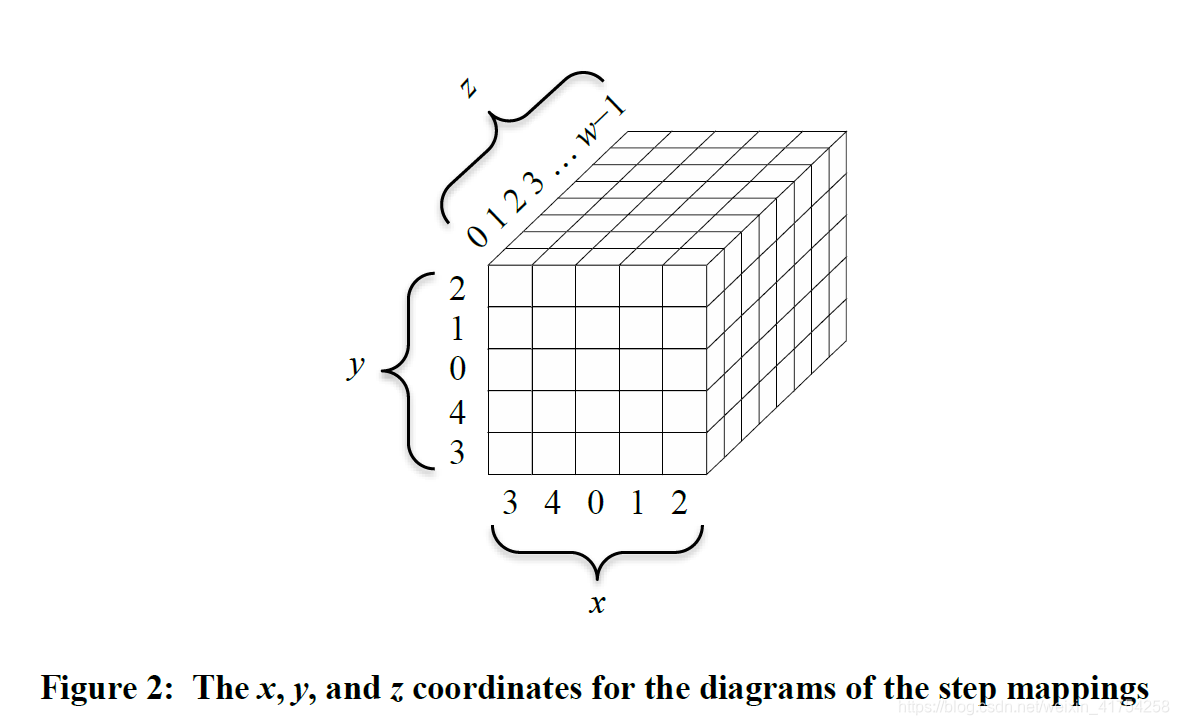
状态数组中的每一位可以用
A
[
x
,
y
,
z
]
A[x,y,z]
A[x,y,z]表示,则有
A
[
i
]
[
j
]
[
k
]
=
S
i
′
[
(
5
j
+
i
)
×
w
+
k
]
A[i][ j][k] =S_i^{'} [(5j + i) × w + k]
A[i][ j][k]=Si′[(5j+i)×w+k],
S
i
′
S_i^{'}
Si′的下标索引采用小端模式,其中
i
i
i表示行,
j
j
j表示列,
k
k
k表示比特。转换的例子如下所示:
那么,如何将状态矩阵又转换成比特串呢?按照
L
a
n
e
(
i
,
j
)
,
P
l
a
n
e
(
j
)
Lane (i, j),Plane (j)
Lane(i,j),Plane(j)和
S
S
S的顺序逐次转换;
L
a
n
e
(
i
,
j
)
=
A
[
i
,
j
,
0
]
∣
∣
A
[
i
,
j
,
1
]
∣
∣
A
[
i
,
j
,
2
]
∣
∣
…
∣
∣
A
[
i
,
j
,
w
−
2
]
∣
∣
A
[
i
,
j
,
w
−
1
]
Lane (i, j) = A[i, j, 0] || A[i, j, 1] || A[i, j, 2] || … || A[i, j, w-2] || A[i, j, w-1]
Lane(i,j)=A[i,j,0]∣∣A[i,j,1]∣∣A[i,j,2]∣∣…∣∣A[i,j,w−2]∣∣A[i,j,w−1],其中
0
≤
i
<
5
,
0
≤
j
<
5
0 ≤ i < 5 ,0 ≤ j < 5
0≤i<5,0≤j<5
P
l
a
n
e
(
j
)
=
L
a
n
e
(
0
,
j
)
∣
∣
L
a
n
e
(
1
,
j
)
∣
∣
L
a
n
e
(
2
,
j
)
∣
∣
L
a
n
e
(
3
,
j
)
∣
∣
L
a
n
e
(
4
,
j
)
Plane (j) = Lane (0, j) || Lane (1, j) || Lane (2, j) || Lane (3, j) || Lane (4, j)
Plane(j)=Lane(0,j)∣∣Lane(1,j)∣∣Lane(2,j)∣∣Lane(3,j)∣∣Lane(4,j),其中
0
≤
j
<
5
0 ≤ j < 5
0≤j<5
S
=
P
l
a
n
e
(
0
)
∣
∣
P
l
a
n
e
(
1
)
∣
∣
P
l
a
n
e
(
2
)
∣
∣
P
l
a
n
e
(
3
)
∣
∣
P
l
a
n
e
(
4
)
S = Plane (0) || Plane (1) || Plane (2) || Plane (3) || Plane (4)
S=Plane(0)∣∣Plane(1)∣∣Plane(2)∣∣Plane(3)∣∣Plane(4)
同样来举个例子吧;
SHA-3 标准中共有 5 个映射函数,可以对状态数组
A
A
A进行不同的排列,下面简要进行介绍。
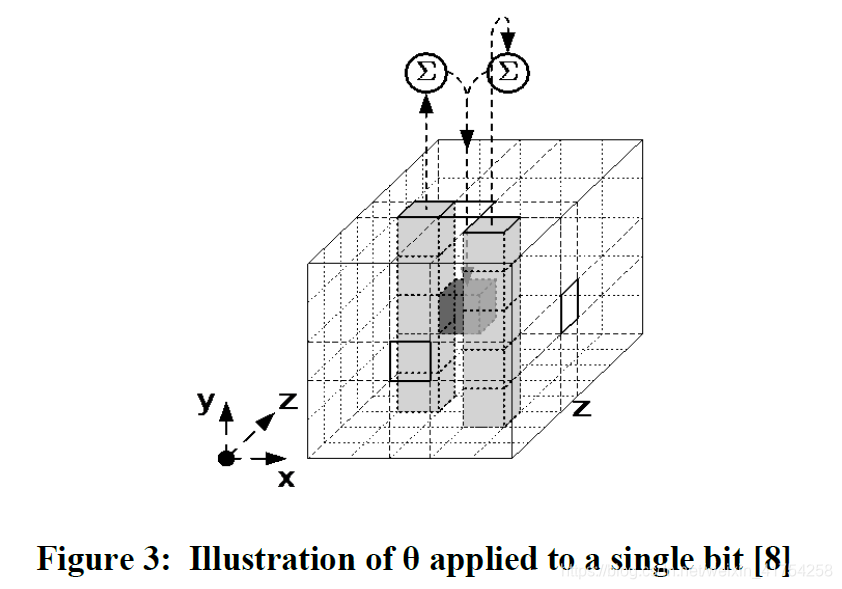
θ ( A ) θ(A) θ(A): 0 ≤ x < 5 , 0 ≤ y < 5 , a n d 0 ≤ z < w 0 ≤ x < 5, 0 ≤ y < 5, and 0 ≤ z < w 0≤x<5,0≤y<5,and0≤z<w
C
[
x
,
z
]
=
A
[
x
,
0
,
z
]
⊕
A
[
x
,
1
,
z
]
⊕
A
[
x
,
2
,
z
]
⊕
A
[
x
,
3
,
z
]
⊕
A
[
x
,
4
,
z
]
C[x, z] = A[x, 0, z] ⊕ A[x, 1, z] ⊕ A[x, 2, z] ⊕ A[x, 3, z] ⊕ A[x, 4, z]
C[x,z]=A[x,0,z]⊕A[x,1,z]⊕A[x,2,z]⊕A[x,3,z]⊕A[x,4,z]
D
[
x
,
z
]
=
C
[
(
x
−
1
)
m
o
d
5
,
z
]
⊕
C
[
(
x
+
1
)
m
o
d
5
,
(
z
–
1
)
m
o
d
w
]
D[x, z] = C[(x-1) mod \ 5, z] ⊕ C[(x+1) mod \ 5, (z – 1) mod\ w]
D[x,z]=C[(x−1)mod 5,z]⊕C[(x+1)mod 5,(z–1)mod w]
A
′
[
x
,
y
,
z
]
=
A
[
x
,
y
,
z
]
⊕
D
[
x
,
z
]
A′[x, y, z] = A[x, y, z] ⊕ D[x, z]
A′[x,y,z]=A[x,y,z]⊕D[x,z]
从图形上来看,就是计算某一比特对应两列的奇偶校验值,再与该比特异或的过程。
ρ
(
A
)
ρ(A)
ρ(A)对25个
L
a
n
e
Lane
Lane进行循环移位:
对于不同
L
a
n
e
Lane
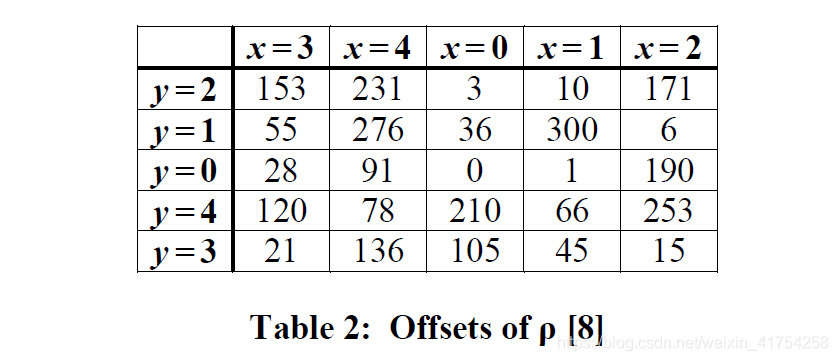
Lane的偏移量是可以预计算的,计算结果如下:
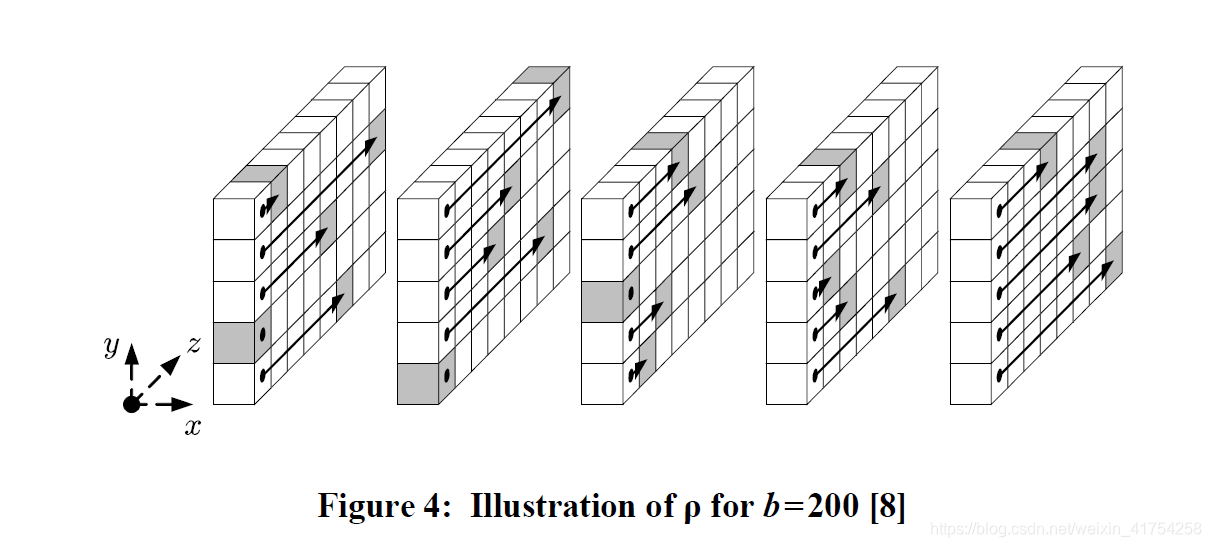
从状态矩阵上来看,图形如下所示,注意是循环移位:
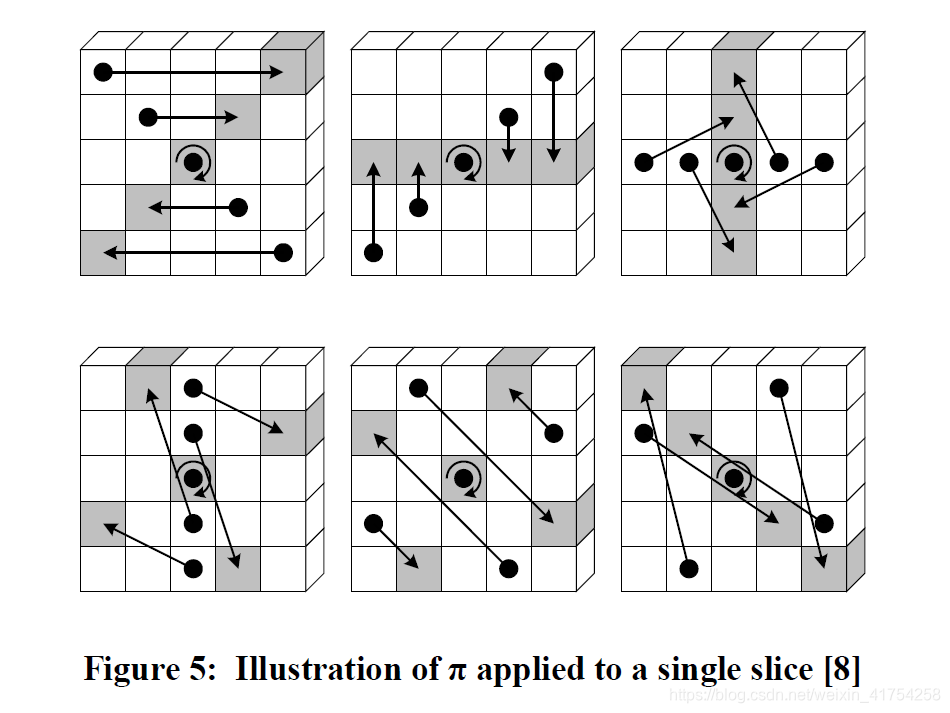
π
(
A
)
π(A)
π(A)对25个
S
l
i
c
e
Slice
Slice进行固定的换位:
从状态矩阵来看,效果如下所示,注意中间点
(
x
,
y
)
=
(
0
,
0
)
(x,y)=(0,0)
(x,y)=(0,0)
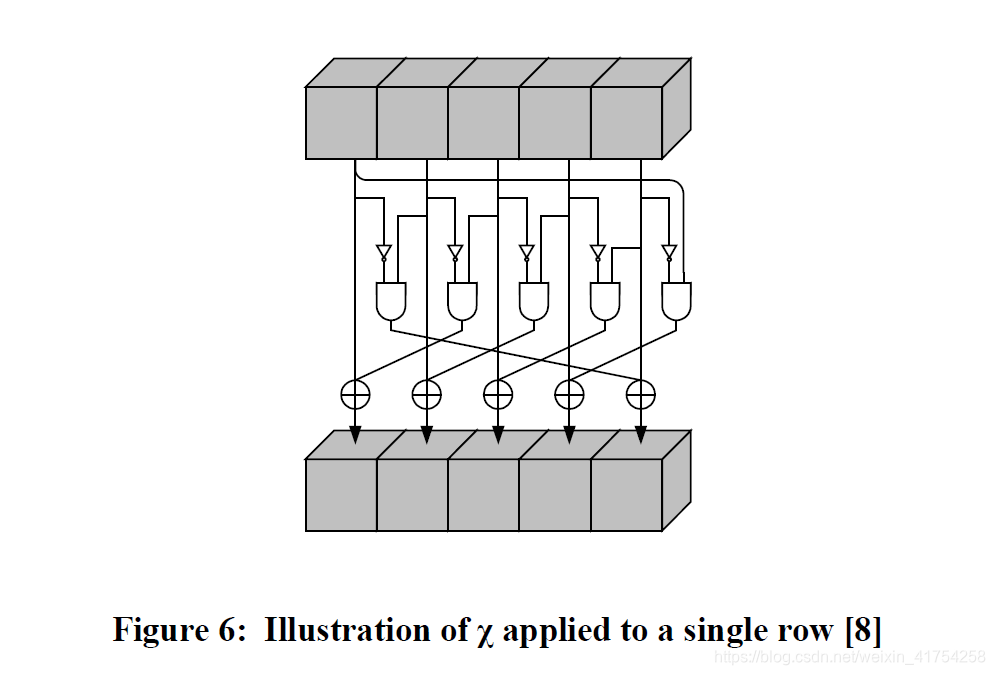
χ
(
A
)
χ(A)
χ(A) 沿
r
o
w
row
row进行比特组合:
从状态矩阵来看,效果如下所示,注意这是对于
x
x
x的:
ι
(
A
,
i
r
)
ι(A,i_r)
ι(A,ir)修改
L
a
n
e
(
0
,
0
)
Lane(0,0)
Lane(0,0)中的某些比特,其他24个
L
a
n
e
(
0
,
0
)
Lane(0,0)
Lane(0,0)则不受影响:
R
C
[
z
]
RC[z]
RC[z]开始被初始化为
w
w
w比特的全
0
0
0,然后对某些比特进行修改,修改后的比特来自于
r
c
(
t
)
rc(t)
rc(t)函数。
r
c
(
t
)
rc(t)
rc(t)函数的定义如下,类似于一个反馈移位寄存器,运算结果为
1
1
1比特,
j
+
7
i
r
j+7i_r
j+7ir是反馈移位寄存器动作的次数。
介绍完5个映射函数,就可以得到轮函数
R
n
d
(
A
,
i
r
)
Rnd(A, i_r)
Rnd(A,ir)了;
定义完
R
n
d
(
A
,
i
r
)
Rnd(A, i_r)
Rnd(A,ir),进一步定义
K
e
c
c
a
k
−
p
[
b
,
n
r
]
Keccak-p[b,n_r]
Keccak−p[b,nr]函数,
K
e
c
c
a
k
−
p
[
b
,
n
r
]
Keccak-p[b,n_r]
Keccak−p[b,nr]是对状态矩阵
A
A
A进行多次
R
n
d
(
A
,
i
r
)
Rnd(A, i_r)
Rnd(A,ir)迭代,
i
r
i_r
ir作为索引,取不同的值;
K
e
c
c
a
k
−
p
[
b
,
n
r
]
Keccak-p[b,n_r]
Keccak−p[b,nr]中的
n
r
n_r
nr是可以取任意正整数的,SHA-3算法中的
f
f
f函数实际上是
K
e
c
c
a
k
−
p
[
b
,
n
r
]
Keccak-p[b,n_r]
Keccak−p[b,nr]的一种特殊化,即
n
r
=
12
+
2
l
n_r=12+2l
nr=12+2l;
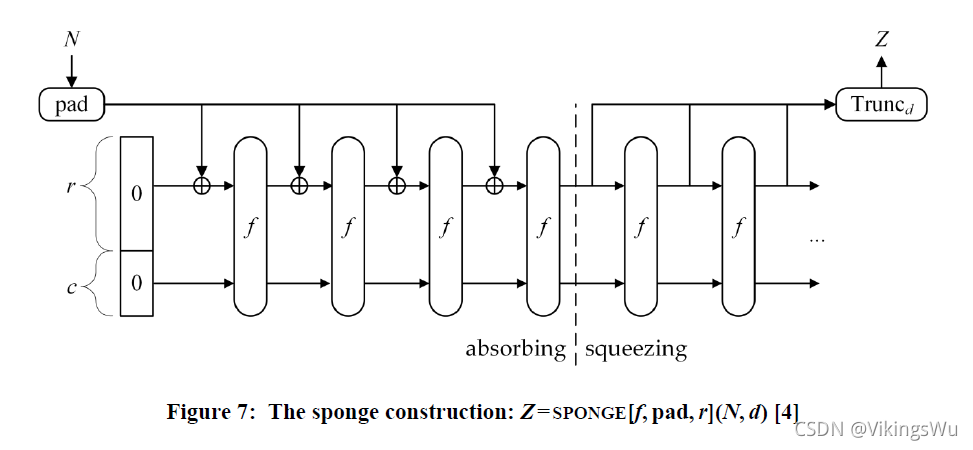
3. 挤压阶段:
挤压阶段和吸收阶段用的是相同的
f
f
f函数。吸收阶段每一个
f
f
f函数之后,将状态矩阵
A
A
A转化成
S
S
S,吸收
r
r
r比特的消息。挤压阶段则每一个
f
f
f函数之后,生成
r
r
r比特的摘要。将生成的摘要进行拼接,直到生成摘要的长度大于需要的摘要长度时,进行截断。
T
r
u
n
c
d
Trunc_d
Truncd表示取字符串的前
d
d
d比特。
4. 总结一下:
3. 需要注意的地方:
-
K
e
c
c
a
k
−
p
[
b
,
n
r
]
Keccak-p[b,n_r]
Keccak−p[b,nr],
K
e
c
c
a
k
−
f
[
b
]
Keccak-f[b]
Keccak−f[b]与
K
e
c
c
a
k
[
c
]
(
N
,
d
)
Keccak{[c]}(N, d)
Keccak[c](N,d)三者的区别需要注意,否则不太容易理解文档中所描述的东西;
K e c c a k − p [ b , n r ] Keccak-p[b,n_r] Keccak−p[b,nr]是广义的置换函数, n r n_r nr是可以取任意正整数的;
SHA-3算法中的 f f f函数实际上是 K e c c a k − p [ b , n r ] Keccak-p[b,n_r] Keccak−p[b,nr]的一种特殊化,即 n r = 12 + 2 l n_r=12+2l nr=12+2l,记为 K e c c a k − f [ b ] Keccak-f[b] Keccak−f[b];
K e c c a k [ c ] ( N , d ) Keccak{[c]}(N, d) Keccak[c](N,d)则可以认为是整体的这种海绵结构,包括吸收和挤压阶段,其中 b = 1600 b=1600 b=1600, c = 1600 − r c=1600-r c=1600−r; S P O N G E SPONGE SPONGE的三个参数分别为 f f f函数、填充规则和 r r r取值,填充规则用正则表达式表示。
K e c c a k [ c ] ( N , d ) Keccak{[c]}(N, d) Keccak[c](N,d)进一步进行限制,则可以定义为SHA-3算法,其中容量 c c c取摘要长度 d d d的两倍;SHA-3在调用 K e c c a k [ c ] ( N , d ) Keccak{[c]}(N, d) Keccak[c](N,d)函数时,需要对消息进行填充01。