目录
1.双变量相关分析
1.1理论基础
双变量相关分析并不是仅仅指的两个变量之间的关系,可以是多个变量之间的关系;
相关分析主要是不关注这个变量之间的因果关系,这个不仅可以用来判断相关性,而且可以去进行预测,而我们后面介绍的这个回归分析就会考虑这个不同变量之间的因果关系;
接下来我们会通过一个温度和日照时长的分析来进行这个相关的关联性的判断;
1.2简单散点图的绘制介绍
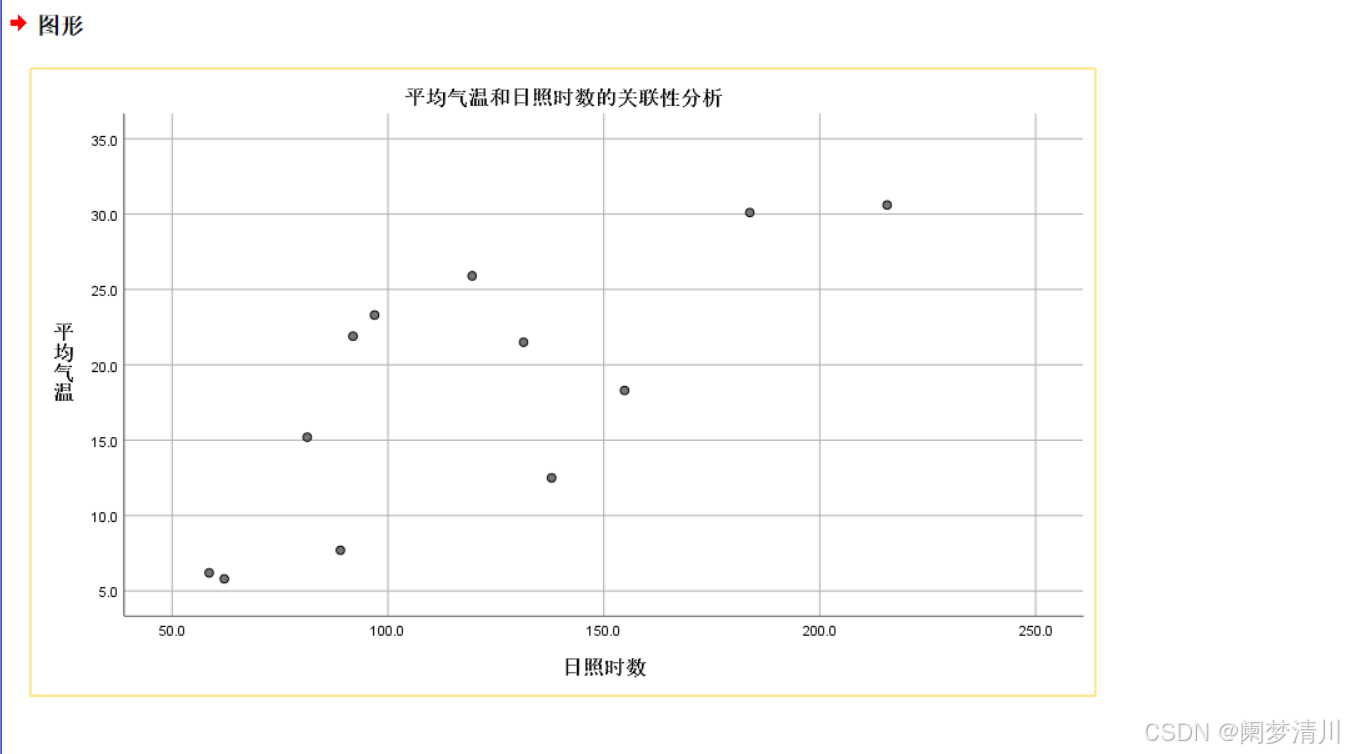
下面就是这个案例的相关数据,我们要判断的就是这个平均气温和日照时数之间的关系;
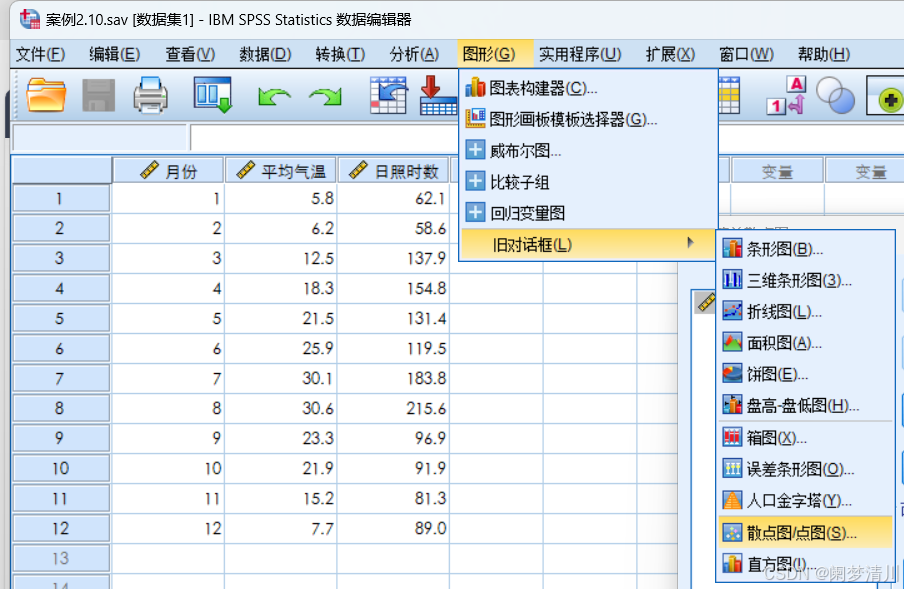
在工具栏里面,我们可以通过相关的选项和操作绘制一个散点图观察一下两个之间的关联效果(虽然可能不是很直观,但是数据的可视化有助于我们后续对于问题的理解分析);
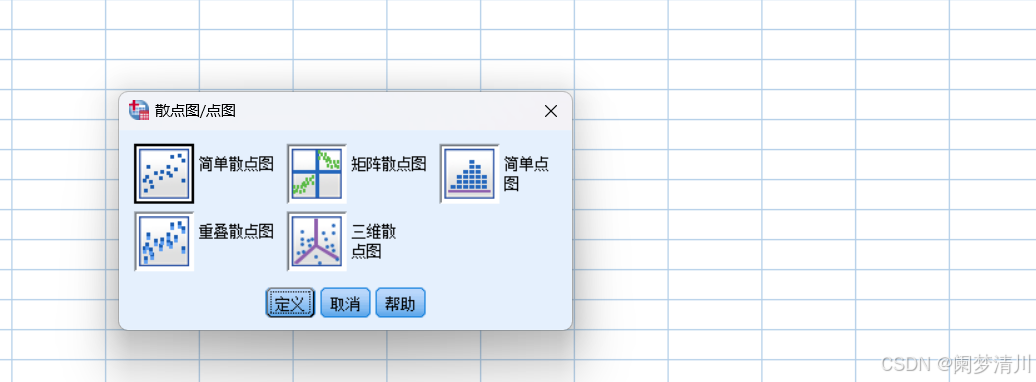
在上面的操作完成之后,就会弹出来这个绘制图形样式的框框,我们只需要选择第一个简单的散点图即可;
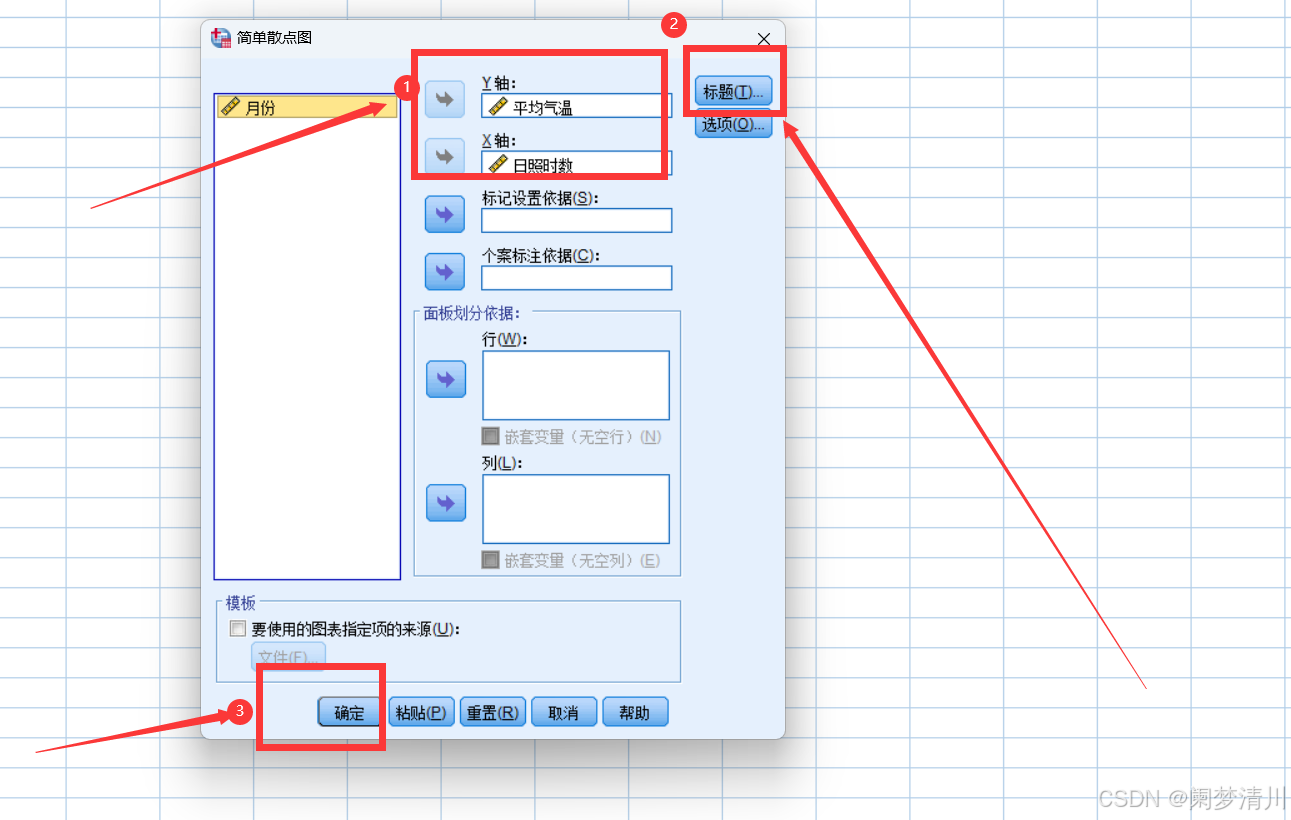
完成相关设置:这个我们要判断的就是平均气温和日照时数的关系,我们肯定是把这个日照时数作为因变量,因为这个日照时数属于自然因素,不是我们认为决定的,他要是作为因变量显然不合适,这个标题想要添加的话是可以进行添加的,不添加也不会影响这个可视化的效果;
直观地看图分析:这个图形的规律并不是很明显,但是这个可见大部分的点都足以佐证这个平均气温是随着日照时数的增加而增加的(当然也有一部分点偏离这个规律,后面我们会进行这个严谨的分析);
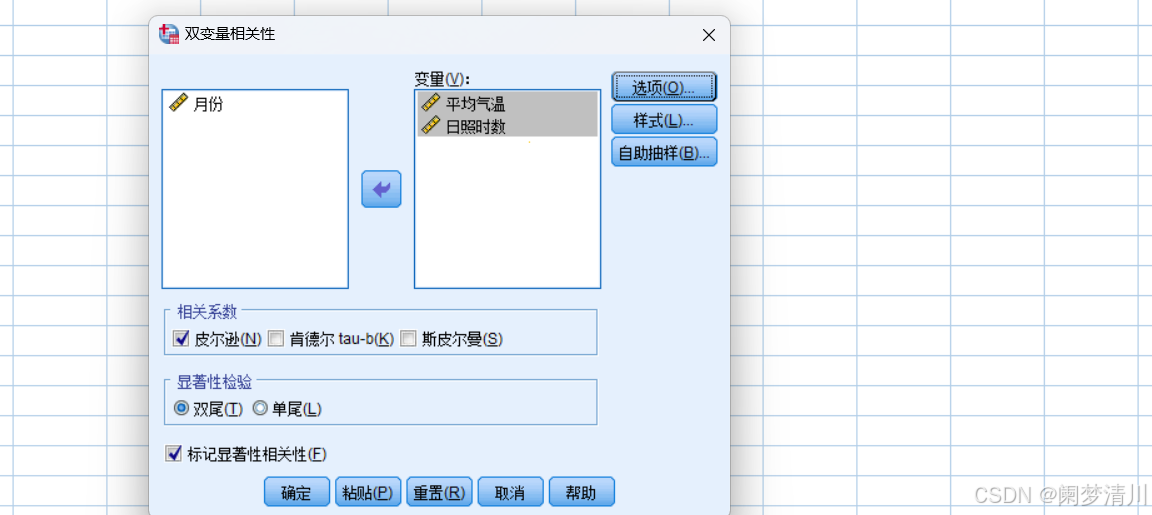
1.3相关性分析
选项里面我们可以勾选一下这个平均值和标注差,可以看到我们使用的这个系数就是皮尔逊系数;
1.4分析相关性结果
这个分析结果里面不仅显示出来了这个描述统计的结果,而且会有相关性的分析结果;
因为我们上面勾选了这个选型里面的平均值和标准差,所以第一个表格里面就会显示出来这个描述性统计的分析结果,相关性分析的这个皮尔逊相关性的数值显示(最后一行也备注了)
2.简单线性回归分析
2.1简单概括
上面的这个简单线性回归研究的是两个变量之间的关系,这个双变量回归分析是可能会有多个变量之间的,但是这个简单线性回归分析就是两个变量之间的关系,这个就是两个方法之间的区别,但是这个两个变量之间的关系既满足简单线性回归分析,也满足双变量相关分析,我们可以两个方法都进行分析一下这个结果;
2.2分析过程
我们要分析的问题如下,就是这个失业率和通货膨胀之间的关系:
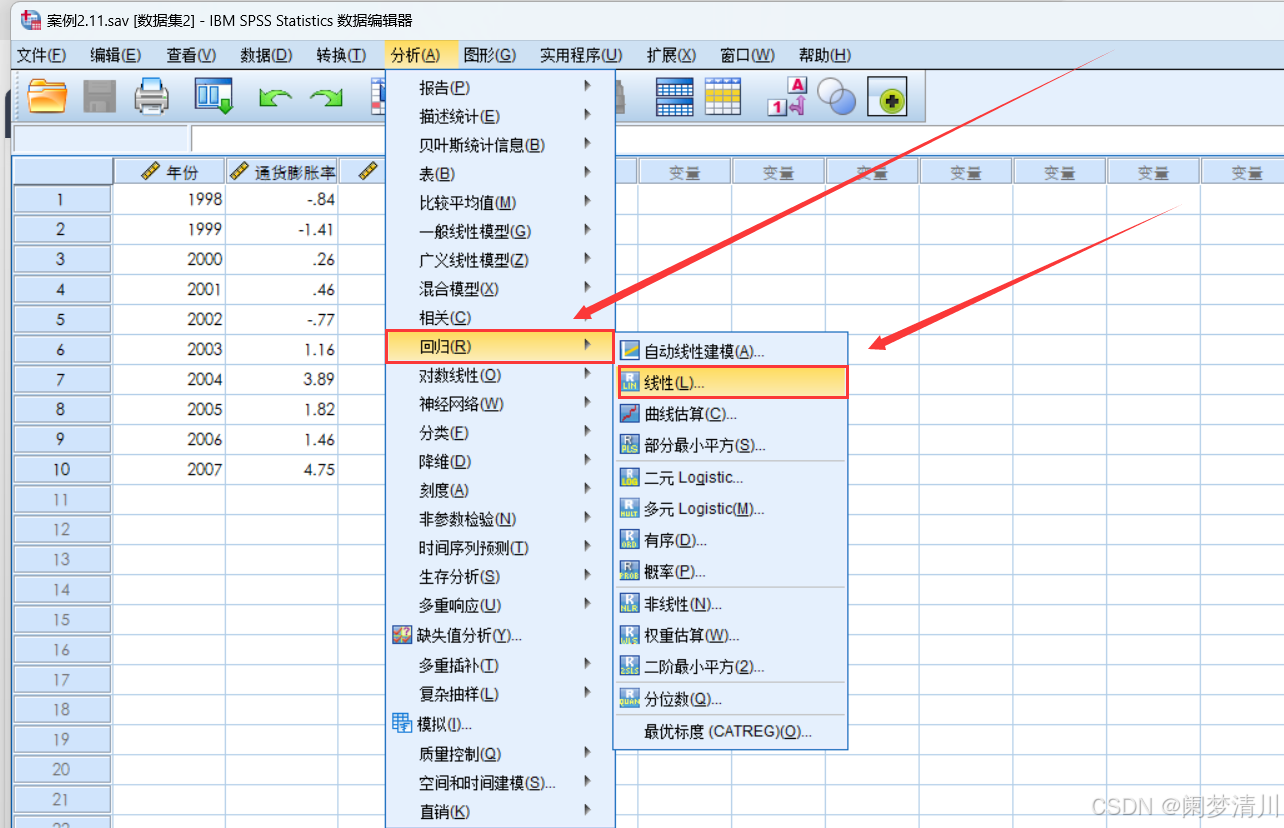
我们直接点击这个分析里面的回归里面的线性;
然后进行这个自变量和因变量的勾选,其他的默认的设置就可以了;
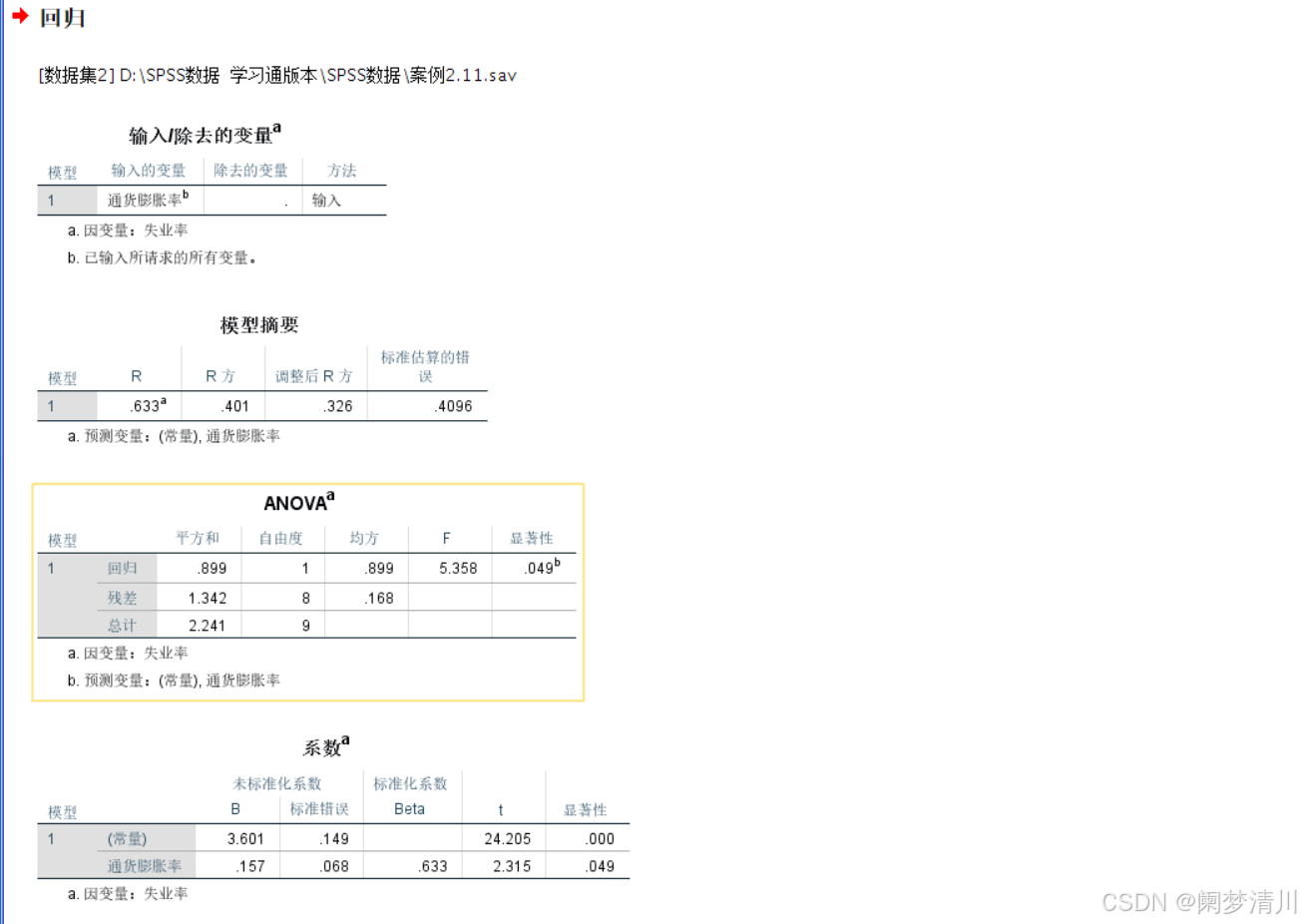
2.3结果分析
我们这个地方研究的对象是失业率,看一看这个通货膨胀对于这个失业率有没有影响,我们的分析结果里面是一共有4个图片,只有第四个才是真的有用,这个里面的常量3.601,通货膨胀率系数0.157这个地方是什么意思呢,我觉得是这个意思:这个简单线性回归分析不要想的太复杂,它实际上就是我们中学时候学习的一次方程y=kx+b,这个肯定没一个人呢都会吧,这个地方的3.601就相当于这个里面的b,0.157就相当于这个k,可以看出来这个斜率还是比较小的,我们就可以去说明这个失业率和通货膨胀率之间没有什么显著的关联;
3.曲线回归分析
3.1问题介绍
3.2分析过程
我们可以按照之前的方法简单的绘制出来一个散点图进行观察,因为这个题目的数据点比较少,所以我们可以根据散点图进行观察,然后再使用这个回归分析的方法;
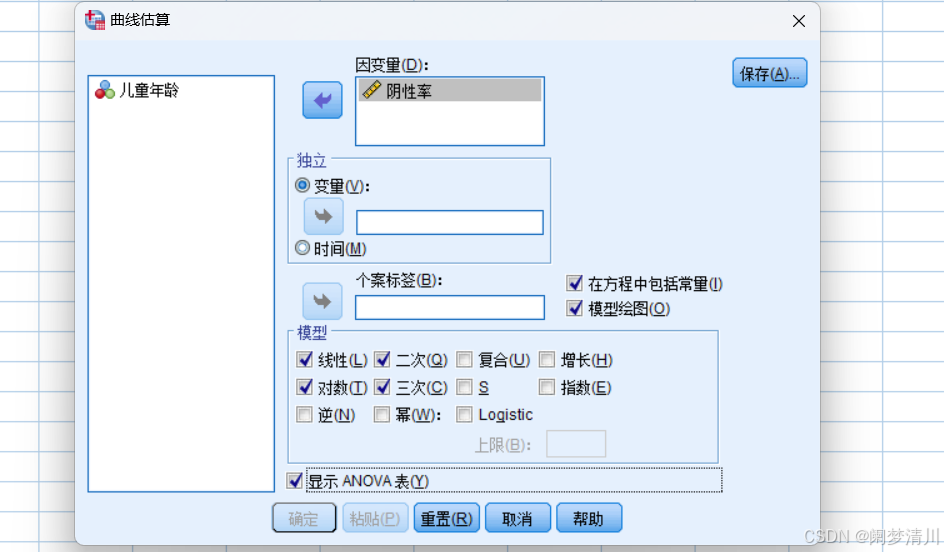
我们这个里面的阴性率是因变量,独立变量就是孩子的年龄,模型的话(这个为啥勾选二次三次,线性,对数,这个就是根据这个散点图的情况大致猜出来的可能情况,就相当于高考数学模拟题里面给你一个函数图像,让你去选择可能的函数解析式,只不过这个地方我们大致的猜一下就行了,不像高考模拟题的时候需要整出这个完整的表达式),我们根据这个散点图,个点之间的分布的情况,我们决定去使用这个二次三次和对数,这个线性是默认的,我们不管就行;
为什么勾选出来这么多种可能的情况,我们根据不同的情况之间的对比分析就可以看出来哪一个对于这个图像的回归分析拟合的效果更好;
3.3结果分析
这个分析的结果还是蛮长的:
每一个(线性,二次,三次,对数)都有三个图,这个分析结果如何去看呢?
首先,我们去看这个每一项的第一个表格里面的R方,这个数据越大表示这个拟合的效果就越好,其次,就是显著性,显著性越接近于0表示这个分析的效果就越好;
综合上面的两个指标,我们就可以断定这个三次拟合的效果最好。