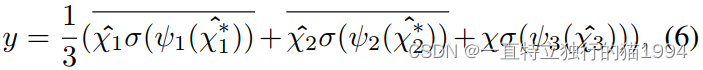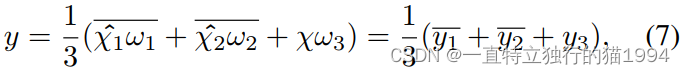CV中的Attention机制总结

注意力机制

注意力机制(Attention Mechanism)是机器学习中的一种数据处理方法，广泛应用在自然语言处理、图像识别及语音识别等各种不同类型的机器学习任务中。注意力机制本质上与人类对外界事物的观察机制相似。通常来说，人们在观察外界事物的时候，首先会比较关注比较倾向于观察事物某些重要的局部信息，然后再把不同区域的信息组合起来，从而形成一个对被观察事物的整体印象。Attention机制最先应用在自然语言处理方面，主要是为了改进文本之间的编码方式，通过编码-解码之后能学习到更好的序列信息，可以参考一篇具有划时代意义的论文：Attention is all you need

Attention Mechanism可以帮助模型对输入的X每个部分赋予不同的权重，抽取出更加关键及重要的信息，使模型做出更加准确的判断，同时不会对模型的计算和存储带来更大的开销，这也是Attention Mechanism应用如此广泛的原因。

总的来说，注意力机制可分为两种：一种是软注意力(soft attention)，另一种则是强注意力(hard attention)。

软注意力(soft attention)与强注意力(hard attention)的不同之处在于：

软注意力更关注区域或者通道，而且软注意力是确定性的注意力，学习完成后直接可以通过网络生成，最关键的地方是软注意力是可微的，这是一个非常重要的地方。可以微分的注意力就可以通过神经网络算出梯度并且前向传播和后向传播来学习得到注意力的权重。在计算机视觉中，很多领域的相关工作(例如，分类、检测、分割、生成模型、视频处理等)都在使用Soft Attention，典型代表：SENet、SKNet。
首先强注意力是更加关注点，也就是图像中的每个点都有可能延伸出注意力，同时强注意力是一个随机的预测过程，更强调动态变化。当然，最关键的是强注意力是一个不可微的注意力，训练过程往往是通过**增强学习(reinforcement learning)**来完成的。

CV中的注意力机制

近几年来，深度学习与视觉注意力机制结合的研究工作，大多数是集中于使用**掩码(mask)**来形成注意力机制。掩码的原理在于通过另一层新的权重，将图片数据中关键的特征标识出来，通过学习训练，让深度神经网络学到每一张新图片中需要关注的区域，也就形成了注意力。

计算机视觉中的注意力机制的基本思想是让模型学会专注，把注意力集中在重要的信息上而忽视不重要的信息。

attention机制的本质就是利用相关特征图学习权重分布，再用学出来的权重施加在原特征图之上最后进行加权求和。不过施加权重的方式略有差别，大致总结为如下四点：

这个加权可以是保留的所有分量均做加权(即soft attention)；也可以是在分布中以某种采样策略选取部分分量(即hard attention)，此时常用RL来做。
加权可以作用在空间尺度上，给不同空间区域加权；
加权可以作用在Channel尺度上，给不同通道特征加权；
加权可以作用在不同时刻历史特征上，结合循环结构添加权重，例如机器翻译，或者视频相关的工作。

为了更清楚地介绍计算机视觉中的注意力机制，通常将注意力机制中的模型结构分为三大注意力域来分析。主要是：空间域(spatial domain)，通道域(channel domain)，混合域(mixed domain)。

①空间域——将图片中的空间域信息做对应的空间变换，从而能将关键的信息提取出来。对空间进行掩码的生成，进行打分，代表是Spatial Attention Module。
②通道域——类似于给每个通道上的信号都增加一个权重，来代表该通道与关键信息的相关度，这个权重越大，则表示相关度越高。对通道生成掩码mask，进行打分，代表是SENet, Channel Attention Module。
③混合域——空间域的注意力忽略了通道域中的信息，将每个通道中的图片特征同等处理，这种做法会将空间域变换方法局限在原始图片特征提取阶段，应用在神经网络层其他层的可解释性不强。

对空间和通道注意力机制的理解

卷积神经网络中常用的Attention

在卷积神经网络中常用的Attention主要有两种：一种是spatial attention, 另外一种是channel attention。当然有时也有使用空间与通道混合的注意力，其中混合注意力的代表主要是BAM, CBAM。

Spatial Attention：
对于卷积神经网络，CNN的每一层都会输出一个CxHxW的特征图，C就是通道，同时也代表卷积核的数量，亦为特征的数量，H和W就是原始图片经过压缩后的图的高度和宽度。spatial attention就是对于所有的通道，在二维平面上，对HxW尺寸的特征图学习到一个权重，对每个像素都会学习到一个权重。可以想象成一个像素是C维的一个向量，深度是C，在C个维度上，权重都是一样的，但是在平面上，权重不一样。

Channel Attention：
就是对每个通道，在通道维度上，学习到不同的权重，平面维度上权重相同。所以基于通道域的注意力通常是对一个通道内的信息直接全局平均池化，而忽略每一个通道内的局部信息。

**spatial和channel attention可以理解为关注图片的不同区域和关注图片的不同特征。**channel attention的全面介绍可以参考论文：SCA-CNN: Spatial and Channel-wise Attention in Convolutional Networks for Image Captioning(CVPR 2017)。通道注意力在图像分类中的应用的网络结构方面，典型的就是SENet。

以上部分讲的太重要了，值得反复研读思考！

======================================================================================
下文将主要介绍：注意力机制在分类网络中的典型应用–SENet

视觉注意力机制在分类网络中的应用

SE-Net(CVPR 2017)

论文题目：Squeeze-and-Excitation Networks
论文地址：https://arxiv.org/abs/1709.01507
官方代码地址：https://github.com/hujie-frank/SENet
PyTorch实现代码：https://github.com/moskomule/senet.pytorch

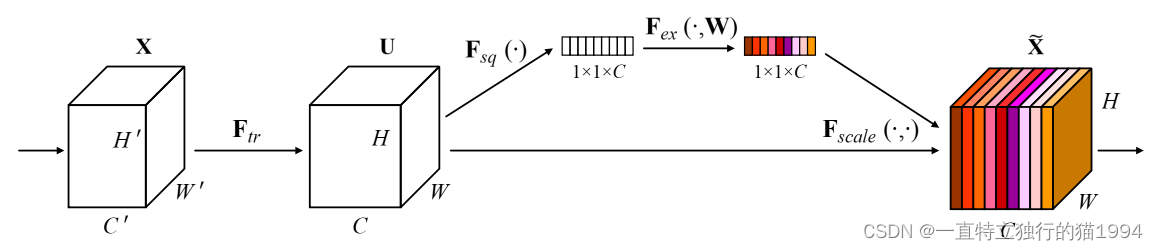
SENet是Squeeze-and-Excitation Networks的简称，由Momenta公司所作并发表于CVPR 2017。论文中的SENet赢得了ImageNet最后一届(ImageNet 2017)的图像识别冠军。SENet主要是学习了channel之间的相关性，筛选出了针对通道的注意力，稍微增加了一点计算量，但是效果比较好。

论文中的motivation: 希望显式地建模特征通道之间的相互依赖关系，通过采用了一种全新的“特征重标定”策略–自适应地重新校准通道的特征响应。具体来说，就是通过学习的方式来自动获取到每个特征通道的重要程度，然后依照这个重要程度去提升有用的特征并抑制对当前任务用处不大的特征。该论文提出的SE模块思想简单，易于实现，并且可以很容易加载到现有的网络模型架构中。
在这里插入图片描述
具体实现方式是：

对输入进来的特征层进行全局平均池化；
然后进行两次全连接，第一次全连接神经元个数较少，第二次全连接神经元个数和输入特征层通道数相同；
在完成两次全连接后，我们再取一次Sigmoid将值固定到0-1之间，此时我们获得了输入特征层每一个通道的权值(0-1之间)；
在获得这个权值后，我们将这个权值乘上原输入特征层即可。

这种结构的原理是想通过控制scale的大小，把重要的特征增强，不重要的特征减弱，从而让提取的特征指向性更强。

SENet 通俗的说就是：通过对卷积之后得到的feature map进行处理，得到一个和通道数一样的一维向量作为每个通道的评价分数，然后将改动之后的分数通过乘法逐通道加权到原来对应的通道上，最后得到输出结果，就相当于在原有的基础上只添加了一个模块而已。

上述模块的PyTorch代码实现：

#----------------------------#
#   SE module的PyTorch实现
#----------------------------#

import torch
from torch import nn
from torchsummary import summary


class SELayer(nn.Module):
    def __init__(self, channel, reduction=16):
        super(SELayer, self).__init__()
        self.avg_pool = nn.AdaptiveAvgPool2d(1)
        self.fc = nn.Sequential(
            nn.Linear(channel, channel // reduction, bias=False),
            nn.ReLU(inplace=True),
            nn.Linear(channel // reduction, channel, bias=False),
            nn.Sigmoid()
        )

    def forward(self, x):
        b, c, h, w = x.size()
        # b, c, h, w -> b, c, 1, 1 -> b, c
        avg_pool_out = self.avg_pool(x).view(b, c)
        # b, c -> b, c // reduction -> b, c -> b, c, 1, 1
        fc_out = self.fc(avg_pool_out).view(b, c, 1, 1)
        # 看一下每个通道的权值
        # print(fc_out)
        return x * fc_out.expand_as(x)


model = SELayer(512)
# print(model)
summary(model, input_size=[(512, 20, 20)], batch_size=1, device="cpu")

inputs = torch.ones([1, 512, 20, 20])
outputs = model(inputs)
print(outputs)

SELayer可以作为一个子模块加载到分类网络的结构中去，具体如下图所示：
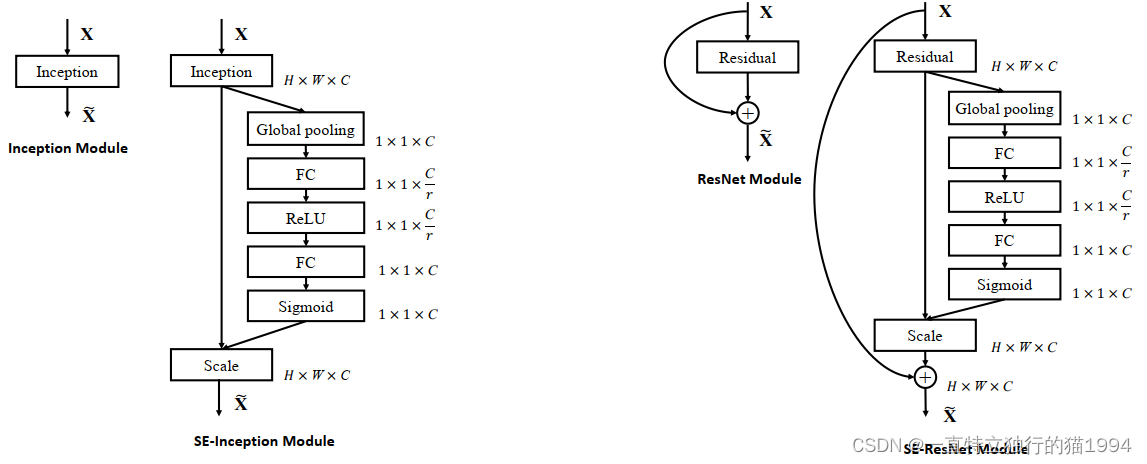
在这里插入图片描述 上面的左图是将SELayer嵌入到Inception结构的一个示例。方框旁边的维度信息代表该层的输出。这里我们使用global average pooling作为Squeeze操作。紧接着两个Fully Connected 层组成一个Bottleneck结构去建模通道间的相关性，并输出和输入特征的通道数同样数目的权重。我们首先将特征维度降低到输入的1/16，然后经过ReLu激活后再通过一个Fully Connected 层升回到原来的维度。

这样做比直接用一个Fully Connected层的好处在于：

具有更多的非线性，可以更好地拟合通道间复杂的相关性；
极大地减少了参数量和计算量。然后通过一个Sigmoid的门获得0-1之间归一化的权重，最后通过一个Scale的操作来将归一化后的权重加权到每个通道的特征上。

除此之外，SELayer还可以嵌入到含有skip-connections的模块中。
上面的右图是将SELayer嵌入到ResNet模块中的一个例子，操作过程基本和SE-Inception一样，只不过是在Addition前对分支上Residual的特征进行了特征重标定。如果对Addition后主支上的特征进行重标定，由于在主干上存在0~1的scale操作，在网络较深的情况下BP算法优化时就会在靠近输入层容易出现梯度消失的情况，导致模型难以被优化。
目前大多数的主流网络都是基于这两种类似的基本单元通过repeat的方式叠加来构造的。由此可见，SELayer可以嵌入到现在几乎所有的网络结构中。通过在原始网络结构的building block单元中嵌入SELayer，我们可以获得不同种类的SENet ，如SE-BN-Inception、SE-ResNet 、SE-ReNeXt、SE-Inception-ResNet-v2等等。

ECA-Net(CVPR 2020)

论文题目：ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks
论文地址：https://arxiv.org/abs/1910.03151
代码地址(PyTorch实现)：https://github.com/BangguWu/ECANet

ECA-Net其实也是通道注意力机制的一种实现形式。ECA-Net可以看作是SE-Net的改进版。

ECA-Net的作者认为：SE-Net对通道注意力机制的预测带来了副作用，捕获所有通道的依赖关系是低效并且是不必要的。在ECA-Net的论文中，作者认为：卷积具有良好的跨通道信息获取能力。

ECA模块的思想是非常简单的，它去除了原来SE模块中的全连接层，直接在全局平均池化之后的特征上通过一个1D卷积进行学习。既然用到了1D卷积，那么1D卷积的卷积核大小的选择就变得非常重要了，了解过卷积原理的同学很快就可以明白，1D卷积的卷积核大小会影响注意力机制每个权重的计算要考虑的通道数量，用更专业的名词就是跨通道交互的覆盖率。

如下图所示，左图是常规的SE模块，右图是ECA模块。ECA模块用1D卷积替换两次全连接。
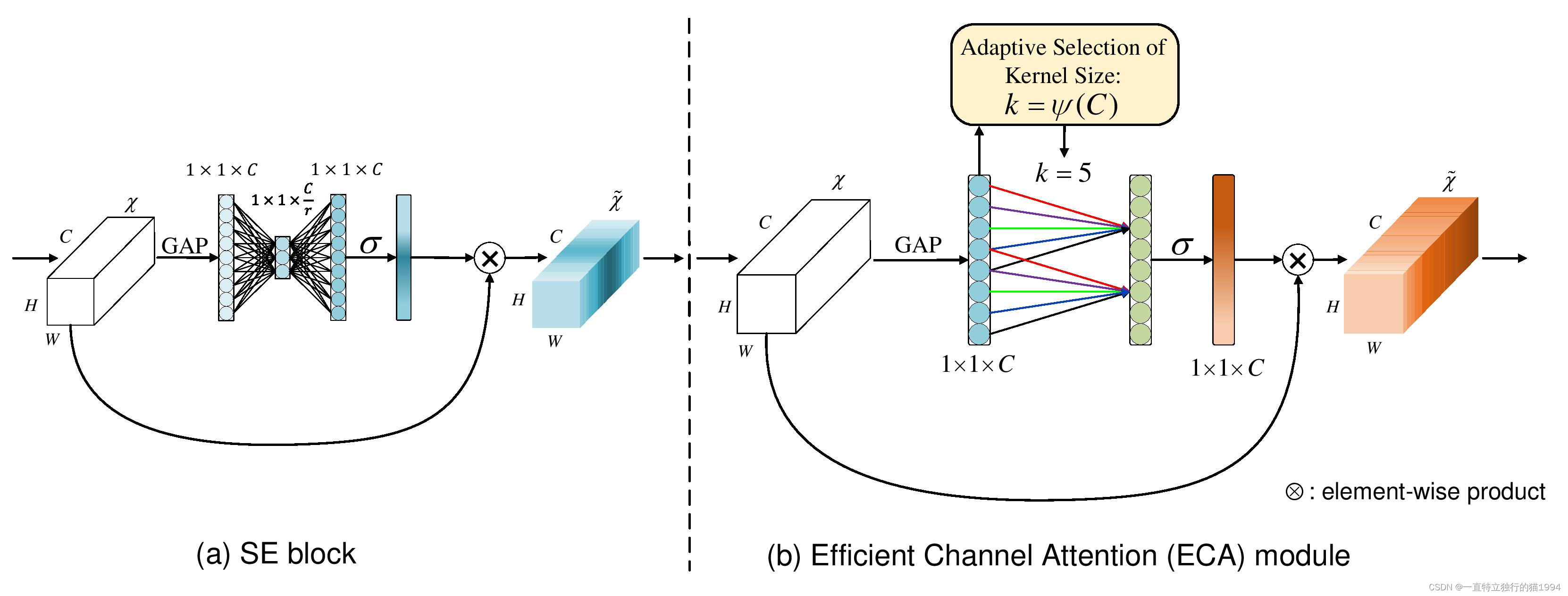
在这里插入图片描述 ECA模块的PyTorch代码实现：

#----------------------------#
#   ECA module的PyTorch实现
#----------------------------#

import torch
from torch import nn
from torchsummary import summary


class ECA_Layer(nn.Module):
    """
    Constructs a ECA module.

    Args:
        channel: Number of channels of the input feature map
        k_size: Adaptive selection of kernel size
    """
    def __init__(self, channel, k_size=3):
        super(ECA_Layer, self).__init__()
        self.avg_pool = nn.AdaptiveAvgPool2d(1)
        self.conv = nn.Conv1d(1, 1, kernel_size=k_size, padding=(k_size - 1) // 2, bias=False)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        # 1, 512, 20, 20 -> 1, 512, 1, 1
        y = self.avg_pool(x)

        # 1, 512, 1, 1 -> 1, 512, 1 -> 1, 1, 512 -> 1, 1, 512 -> 1, 512, 1 -> 1, 512, 1, 1
        y = self.conv(y.squeeze(-1).transpose(-1, -2)).transpose(-1, -2).unsqueeze(-1)

        # 1, 512, 1, 1 -> 1, 512, 1, 1
        y = self.sigmoid(y)

        # 看一下权重
        # print(y)

        return x * y.expand_as(x)


model = ECA_Layer(512)
# print(model)
summary(model, input_size=[(512, 20, 20)], batch_size=1, device="cpu")

inputs = torch.rand([1, 512, 20, 20])
outputs = model(inputs)
print(outputs)

CBAM(ECCV 2018)

论文题目：CBAM: Convolutional Block Attention Module
论文地址：https://arxiv.org/pdf/1807.06521.pdf

请查看我另一篇关于CBAM的文章：CBAM的理解、Pytorch实现及用法

BAM(BMCV 2018)

论文题目：BAM: Bottleneck Attention Module
论文地址：https://arxiv.org/abs/1807.06514
官方源码地址(PyTorch)：https://github.com/Jongchan/attention-module

简介

这是CBAM同作者同时期的工作，两者属于姊妹篇，与CBAM非常相似，也是双重attention(空间+通道)，不同的是CBAM是将两个attention的结果串联，而BAM是直接将两个attention矩阵进行相加。
BAM的整体结构如下：
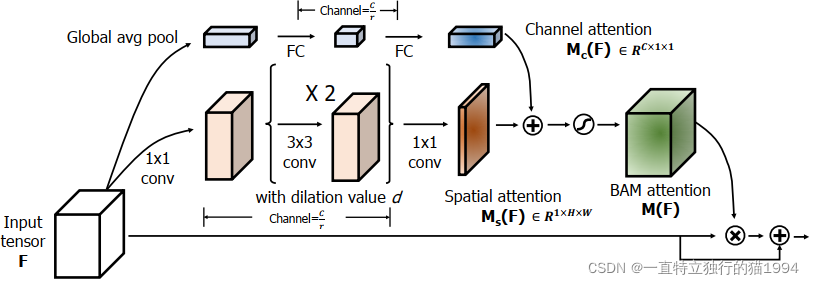
在这里插入图片描述 $F'=F+F\otimes M(F)$ $M(F)=\sigma(M_c(F)+M_s(F))$
下面我们根据这个整体结构图分为Channel attention branch和Spatial attention branch进行介绍。

通道注意力分支

通道注意力的计算如下：
$M_c(F)=BN(MLP(AvgPool(F)))=BN(W_1(W_0AvgPool(F)+b_0)+b_1)$ 其中， $W_0\in R^{C/r\times C}$ ， $b_0\in R^{C/r}$ ， $W_1\in R^{C \times C/r}$ ， $b_1\in R^{C}$ .

空间注意力分支

空间注意力的计算如下：
$M_s(F)=BN(f_3^{1\times1}(f_2^{3\times3}(f_1^{3\times3}(f_0^{1\times1}(F)))))$

官方PyTorch实现代码

#---------------------------#
#    BAM的官方PyTorch实现
#---------------------------#
import torch
import math
import torch.nn as nn
import torch.nn.functional as F


class Flatten(nn.Module):
    def forward(self, x):
        return x.view(x.size(0), -1)


class ChannelGate(nn.Module):
    def __init__(self, gate_channel, reduction_ratio=16, num_layers=1):
        super(ChannelGate, self).__init__()
        self.gate_c = nn.Sequential()
        # after avg_pool
        self.gate_c.add_module('flatten', Flatten())
        gate_channels = [gate_channel]
        gate_channels += [gate_channel // reduction_ratio] * num_layers
        gate_channels += [gate_channel]
        # print("gate_channels的形状：", gate_channels)
        for i in range(len(gate_channels) - 2):
            # 第一个FC
            self.gate_c.add_module('gate_c_fc_%d' % i, nn.Linear(gate_channels[i], gate_channels[i+1]))
            self.gate_c.add_module('gate_c_bn_%d' % (i+1), nn.BatchNorm1d(gate_channels[i+1]))
            self.gate_c.add_module('gate_c_relu_%d' % (i+1), nn.ReLU())
        # 第二个FC
        self.gate_c.add_module('gate_c_fc_final', nn.Linear(gate_channels[-2], gate_channels[-1]))

    def forward(self, in_tensor):
        # Global avg pool, shape变化: C*H*W -> C*1*1
        avg_pool = F.avg_pool2d(in_tensor, in_tensor.size(2), stride=in_tensor.size(2))
        # print("全局平均池化后的形状：", avg_pool.shape)
        # C*1*1 -> C*H*W
        # print("self.gate_c(avg_pool)的形状:", self.gate_c(avg_pool).shape)
        # print("self.gate_c(avg_pool).unsqueeze(2).unsqueeze(3).expand_as(in_tensor):",
        #       self.gate_c(avg_pool).unsqueeze(2).unsqueeze(3).expand_as(in_tensor).shape)
        return self.gate_c(avg_pool).unsqueeze(2).unsqueeze(3).expand_as(in_tensor)


class SpatialGate(nn.Module):
    # dilation value and reduction ratio, set d = 4 and r = 16
    def __init__(self, gate_channel, reduction_ratio=16, dilation_conv_num=2, dilation_val=4):
        super(SpatialGate, self).__init__()
        self.gate_s = nn.Sequential()
        # 一个1*1的卷积
        self.gate_s.add_module('gate_s_conv_reduce0', nn.Conv2d(gate_channel, gate_channel//reduction_ratio, kernel_size=1))
        self.gate_s.add_module('gate_s_bn_reduce0',	nn.BatchNorm2d(gate_channel//reduction_ratio))
        self.gate_s.add_module('gate_s_relu_reduce0', nn.ReLU())
        # 两个3*3的卷积
        for i in range(dilation_conv_num):
            self.gate_s.add_module('gate_s_conv_di_%d' % i, nn.Conv2d(gate_channel//reduction_ratio, gate_channel//reduction_ratio, kernel_size=3,
                                                                      padding=dilation_val, dilation=dilation_val))
            self.gate_s.add_module('gate_s_bn_di_%d' % i, nn.BatchNorm2d(gate_channel//reduction_ratio))
            self.gate_s.add_module('gate_s_relu_di_%d' % i, nn.ReLU())
        # 最后一个1*1的卷积
        self.gate_s.add_module('gate_s_conv_final', nn.Conv2d(gate_channel//reduction_ratio, 1, kernel_size=1))  # 1*H*W

    def forward(self, in_tensor):
        # print("最后一个1*1的卷积后的形状：", self.gate_s(in_tensor).shape)
        # print("self.gate_s(in_tensor).expand_as(in_tensor):",
        #       self.gate_s(in_tensor).expand_as(in_tensor).shape)
        return self.gate_s(in_tensor).expand_as(in_tensor)


class BAM(nn.Module):
    def __init__(self, gate_channel):
        super(BAM, self).__init__()
        self.channel_att = ChannelGate(gate_channel)
        self.spatial_att = SpatialGate(gate_channel)

    def forward(self, in_tensor):
        # att = 1 + F.sigmoid(self.channel_att(in_tensor) * self.spatial_att(in_tensor))  # F.有报警
        att = 1 + torch.sigmoid(self.channel_att(in_tensor) + self.spatial_att(in_tensor))  # 改成了加号，官方代码是乘号
        return att * in_tensor


if __name__ == "__main__":
    print('-----------------------测试一下-----------------------------')
    bam = BAM(32)
    input = torch.randn(8, 32, 300, 300)
    output = bam(input)
    print("BAM输入的形状：", input.shape)  # 输入的形状
    print("BAM输出的形状：", output.shape)  # 输出的形状

GAM(arXiv 2021)

论文题目：Global Attention Mechanism: Retain Information to Enhance Channel-Spatial Interactions
论文链接：https://arxiv.org/pdf/2112.05561.pdf

动机

为了提高各种计算机视觉任务的性能，人们研究了各种注意力机制。然而，之前的方法忽略了保留通道和空间方面的信息以增强跨维度交互的重要性。因此，本文提出了一种通过减少信息的损失和放大全局交互表示来提高深度神经网络性能的全局注意力机制。SENet是第一个使用通道注意和通道特征融合来抑制不重要通道的网络。然而，它在抑制不重要的像素方面效率较低。CBAM依次放置通道和空间注意操作，而BAM并行执行。然而，它们都忽略了通道-空间相互作用，从而丢失了跨维度信息。考虑到跨维度交互的重要性，三重注意力模块(TAM)通过利用三个维度（通道、空间宽度和空间高度）中每对之间的注意力权重来提高效率。然而，注意力操作仍然每次都应用在两个维度上，而不是全部三个。为了放大跨维度交互，我们提出了一种能够捕获所有三个维度的重要特征的注意力机制。

我们的目标是设计一种减少信息损失并放大全局维度交互特征的机制。我们采用CBAM的顺序通道空间注意机制并重新设计子模块。

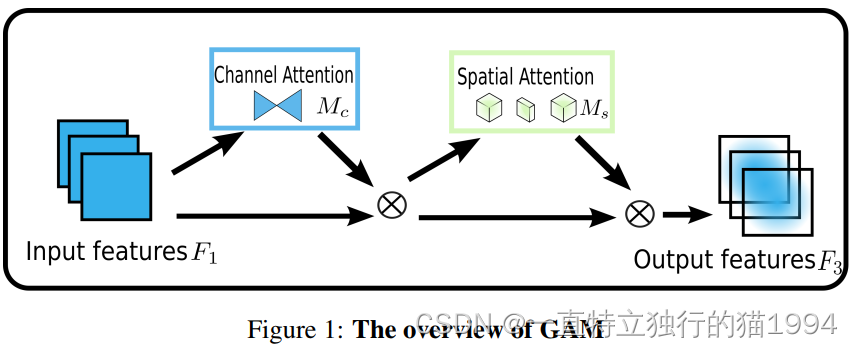
全局注意力机制(GAM)

GAM的总体示意图如下：
在这里插入图片描述
给定输入特征图 $\mathbf{F_1} \in\mathbb{R}^{C\times H\times\ W}$ ，中间状态 $\mathbf{F_2}$ 和输出 $\mathbf{F_3}$ 定义为： $\mathbf{F_2}=\mathbf{M_c(F_1)}\otimes\mathbf{F_1}$ $\mathbf{F_3}=\mathbf{M_s(F_2)}\otimes\mathbf{F_2}$
其中， $\mathbf{M_c}$ 和 $\mathbf{M_s}$ 分别表示通道和空间注意图， $\otimes$ 表示按元素进行乘法操作。

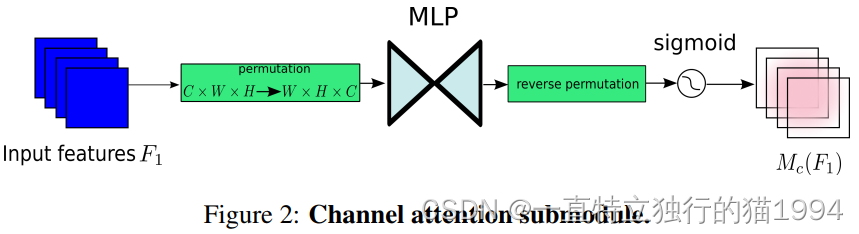
通道注意力子模块

通道注意力子模块如下图2所示：
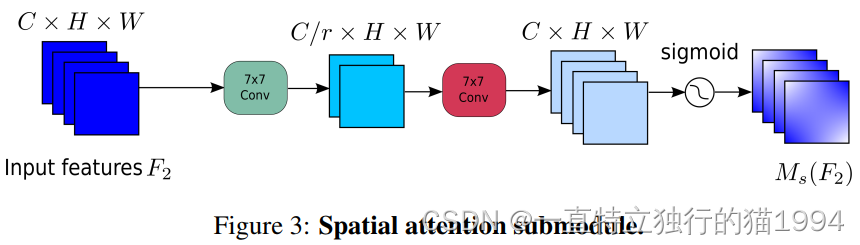
在这里插入图片描述

空间注意力子模块

空间注意力子模块如下图3所示：
在这里插入图片描述

GAM注意力机制的PyTorch实现

import torch.nn as nn
import torch


# GAM注意力机制
class GAM_Attention(nn.Module):
    def __init__(self, in_channels, out_channels, rate=4):
        super(GAM_Attention, self).__init__()

        # 通道注意力
        self.channel_attention = nn.Sequential(
            nn.Linear(in_channels, int(in_channels / rate)),
            nn.ReLU(inplace=True),
            nn.Linear(int(in_channels / rate), in_channels)
        )

        # 空间注意力
        self.spatial_attention = nn.Sequential(
            nn.Conv2d(in_channels, int(in_channels / rate), kernel_size=7, padding=3),
            nn.BatchNorm2d(int(in_channels / rate)),
            nn.ReLU(inplace=True),
            nn.Conv2d(int(in_channels / rate), out_channels, kernel_size=7, padding=3),
            nn.BatchNorm2d(out_channels)
        )

    def forward(self, x):
        b, c, h, w = x.shape
        # permutation
        x_permute = x.permute(0, 2, 3, 1).view(b, -1, c)
        # print('x_permute的形状：', x_permute.shape)
        x_att_permute = self.channel_attention(x_permute).view(b, h, w, c)
        # print('x_att_permute的形状：', x_att_permute.shape)
        # reverse permutation
        x_channel_att = x_att_permute.permute(0, 3, 1, 2)
        # print('x_channel_att的形状：', x_channel_att.shape)
        x_channel_att = x_channel_att.sigmoid()  # 网上的好多GAM代码给通道注意力都没有加sigmoid
        # print('通道注意力：', x_channel_att)

        x = x * x_channel_att

        x_spatial_att = self.spatial_attention(x).sigmoid()
        out = x * x_spatial_att

        return out


if __name__ == '__main__':
    """
    测试一下
    """
    x = torch.randn(1, 64, 32, 48)
    b, c, h, w = x.shape
    net = GAM_Attention(in_channels=c, out_channels=c)
    y = net(x)

CA(CVPR 2021)

动机

Mobile Network设计的最新研究成果表明，通道注意力（例如，SE注意力）对于提升模型性能具有显著效果，但它们通常会忽略位置信息，而位置信息对于生成空间选择性attention maps是非常重要的。因此，作者通过将位置信息嵌入到通道注意力中提出了一种新颖的移动网络注意力机制，将其称为“Coordinate Attention”。

与通过2维全局池化将特征张量转换为单个特征向量的通道注意力不同，coordinate attention将通道注意力分解为两个1维特征编码过程，分别沿2个空间方向聚合特征。这样，可以沿一个空间方向捕获远程依赖关系，同时可以沿另一空间方向保留精确的位置信息。然后将生成的特征图分别编码为一对方向感知和位置敏感的attention map，可以将其互补地应用于输入特征图，以增强关注对象的表示。

Coordinate Attention通过精确的位置信息对通道关系和长期依赖性进行编码，具体操作分为Coordinate信息嵌入和Coordinate Attention生成2个步骤。

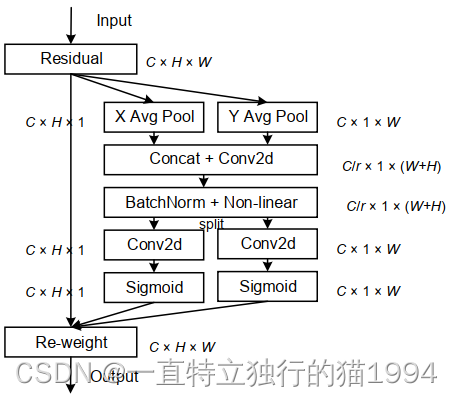
Coordinate信息嵌入

全局池化方法通常用于通道注意编码空间信息的全局编码，但由于它将全局空间信息压缩到通道描述符中，导致难以保存位置信息。为了促使注意力模块能够捕捉具有精确位置信息的远程空间交互，本文按照以下公式分解了全局池化，转化为一对一维特征编码操作：
$z_c=\frac{1}{H\times W}\sum_{i=1}^H\sum_{j=1}^Wx_c(i,j)$
具体来说，给定输入 $X$ ，首先使用尺寸为(H,1)或(1,W)的pooling kernel分别沿着水平坐标和垂直坐标对每个通道进行编码。因此，高度为 $h$ 的第 $c$ 通道的输出可以表示为：
$z_c^h(h)=\frac{1}{W}\sum_{0\leq i<W}x_c(h,i).$
同样，宽度为 $w$ 的第 $c$ 通道的输出可以写成：
$z_c^w(w)=\frac{1}{H}\sum_{0\leq j<H}x_c(j,w).$
上述2种变换分别沿两个空间方向聚合特征，得到一对方向感知的特征图。这与在通道注意力方法中产生单一的特征向量的SE Block非常不同。这2种转换允许注意力模块捕捉到沿着一个空间方向的长期依赖关系，并保存沿着另一个空间方向的精确位置信息，这有助于网络更准确地定位感兴趣的目标。

Coordinate Attention生成

本文方法可以通过上述的变换很好的获得全局感受野并编码精确的位置信息。为了利用由此产生的表征，提出了第2个转换，称为Coordinate Attention生成。这里的设计主要参考了以下3个标准：

首先，对于Mobile环境中的应用来说，新的转换应该尽可能地简单；
其次，它可以充分利用捕获到的位置信息，使感兴趣的区域能够被准确地捕获；
最后，它还应该能够有效地捕捉通道间的关系。
通过Coordinate信息嵌入中的变换后，该部分将上面的变换进行concatenate操作，然后使用 $1\times 1$ 卷积变换函数 $F_1$ 对其进行变换操作：
$\mathbf{f}=\delta(F_1([\mathbf{z}^h,\mathbf{z}^w])),$
式中 $[\cdot,\cdot]$ 为沿空间维度的concatenate操作， $\delta$ 为非线性激活函数， $F_1$ 为对空间信息在水平方向和垂直方向进行编码的中间特征映射。然后沿着空间维度将 $\mathbf{f}$ 分解为2个单独的张量 $\mathbf{f}^h\in R^{C/r\times W}$ 和 $\mathbf{f}^w\in R^{C/r\times W}$ 。这里， $r$ 是用来控制SE block大小的缩减率。利用另外2个 $1\times 1$ 卷积变换 $F_h$ 和 $F_w$ 分别将 $\mathbf{f}^h$ 和 $\mathbf{f}^w$ 变换为具有相同通道数的张量到输入 $X$ ，得到：
$\mathbf{g}^h=\sigma(F_h(\mathbf{f}^h)),$ $\mathbf{g}^w=\sigma(F_w(\mathbf{f}^w)).$
这里 $\sigma$ 是sigmoid激活函数。为了降低模型的复杂性和计算开销，这里通常使用适当的缩减比 $r$ (如32)来减少 $\mathbf{f}$ 的通道数。然后对输出 $\mathbf{g}^h$ 和 $\mathbf{g}^w$ 进行扩展，分别作为attention weights。最后，Coordinate Attention Block的输出 $Y$ 可以写成：
$y_c(i,j)=x_c(i,j)\times g_c^h(i)\times g_c^w(j).$

CA Block的PyTorch实现

# CA注意力机制
class h_sigmoid(nn.Module):
    def __init__(self, inplace=True):
        super(h_sigmoid, self).__init__()
        self.relu = nn.ReLU6(inplace=inplace)

    def forward(self, x):
        return self.relu(x + 3) / 6


class h_swish(nn.Module):
    def __init__(self, inplace=True):
        super(h_swish, self).__init__()
        self.sigmoid = h_sigmoid(inplace=inplace)

    def forward(self, x):
        return x * self.sigmoid(x)


class CA(nn.Module):
    def __init__(self, inp, oup, reduction=32):
        super(CA, self).__init__()
        self.pool_h = nn.AdaptiveAvgPool2d((None, 1))
        self.pool_w = nn.AdaptiveAvgPool2d((1, None))

        mip = max(8, inp // reduction)

        self.conv1 = nn.Conv2d(inp, mip, kernel_size=1, stride=1, padding=0)
        self.bn1 = nn.BatchNorm2d(mip)
        self.act = h_swish()

        self.conv_h = nn.Conv2d(mip, oup, kernel_size=1, stride=1, padding=0)
        self.conv_w = nn.Conv2d(mip, oup, kernel_size=1, stride=1, padding=0)

    def forward(self, x):
        identity = x

        n, c, h, w = x.size()
        # ---------------------------#
        # 加这两行，让它强制进入else语句
        if h <= 16:
            out = x
        # ---------------------------#
        else:
            x_h = self.pool_h(x)
            x_w = self.pool_w(x).permute(0, 1, 3, 2)

            y = torch.cat([x_h, x_w], dim=2)
            y = self.conv1(y)
            y = self.bn1(y)
            y = self.act(y)

            x_h, x_w = torch.split(y, [h, w], dim=2)
            x_w = x_w.permute(0, 1, 3, 2)

            a_h = self.conv_h(x_h).sigmoid()
            a_w = self.conv_w(x_w).sigmoid()

            out = identity * a_w * a_h

        return out

TAM(WACV 2021)

论文链接：https://arxiv.org/pdf/2010.03045.pdf
代码链接(官方)：https://github.com/LandskapeAI/triplet-attention

简介

三重注意力是一种通过使用一个三分支结构捕获跨维度相互作用来计算注意力权重的新方法。对于一个输入张量，三重注意力通过旋转操作建立维度间的相关性，然后进行残差变换，并以可忽略的计算开销编码通道维度和空间维度之间的信息。实验验证了在计算注意力权重时捕获跨维度依赖性的重要性。

三重注意力模块

这项工作的目的是研究如何在不涉及任何降维的情况下对便宜但有效的通道注意力进行建模。与CBAM和SENet不同，CBAM和SENet需要一定数量的可学习参数来建立通道之间的相互依赖关系，作者提出了一种几乎无参数的注意力机制来建模通道注意力和空间注意力，即三重注意力。

所提出的三重注意力如图所示：
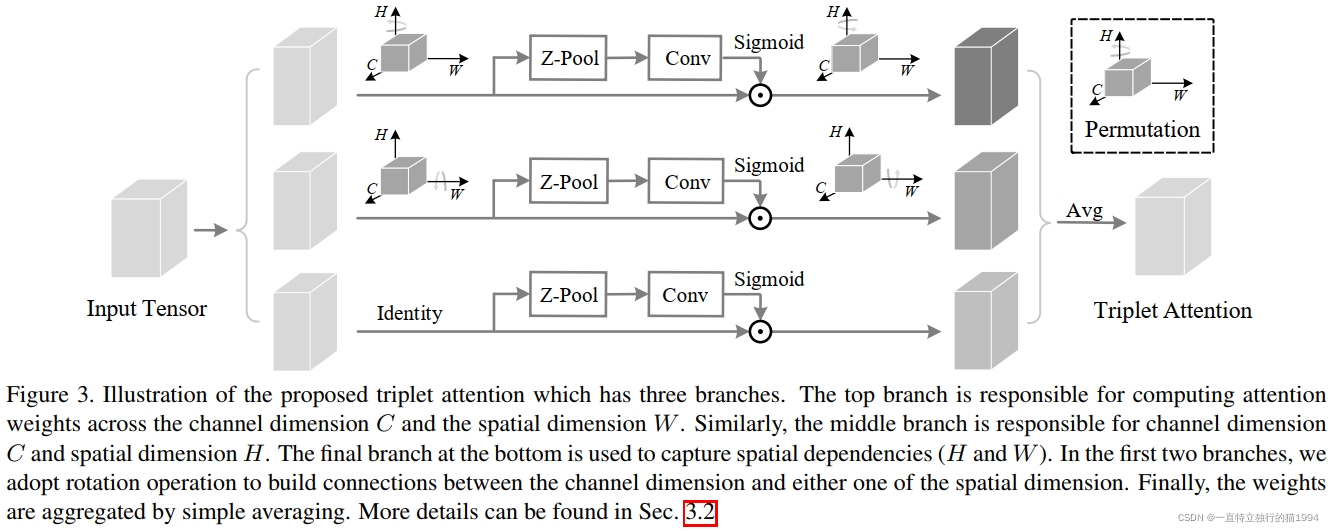
在这里插入图片描述三重注意力由三个平行分支组成，其中两个分支负责捕获通道维度 $C$ 和空间维度 $H$ 或 $W$ 之间的跨维度相互作用。剩下的最后一个分支类似于CBAM，用于建立空间注意力。三个分支的输出使用简单的平均进行汇总。具体的形状变换可以由下图清晰地表达：

总之，以上的过程可以由以下两个公式来表达：
在这里插入图片描述

TAM的PyTorch代码实现(官方)

import torch
import torch.nn as nn


class BasicConv(nn.Module):
    def __init__(
        self,
        in_planes,
        out_planes,
        kernel_size,
        stride=1,
        padding=0,
        dilation=1,
        groups=1,
        relu=True,
        bn=True,
        bias=False,
    ):
        super(BasicConv, self).__init__()
        self.out_channels = out_planes
        self.conv = nn.Conv2d(
            in_planes,
            out_planes,
            kernel_size=kernel_size,
            stride=stride,
            padding=padding,
            dilation=dilation,
            groups=groups,
            bias=bias,
        )
        self.bn = (
            nn.BatchNorm2d(out_planes, eps=1e-5, momentum=0.01, affine=True)
            if bn
            else None
        )
        self.relu = nn.ReLU() if relu else None

    def forward(self, x):
        x = self.conv(x)
        if self.bn is not None:
            x = self.bn(x)
        if self.relu is not None:
            x = self.relu(x)
        return x


class ZPool(nn.Module):
    def forward(self, x):
        return torch.cat(
            (torch.max(x, 1)[0].unsqueeze(1), torch.mean(x, 1).unsqueeze(1)), dim=1
        )


class AttentionGate(nn.Module):
    def __init__(self):
        super(AttentionGate, self).__init__()
        kernel_size = 7
        self.compress = ZPool()
        self.conv = BasicConv(
            2, 1, kernel_size, stride=1, padding=(kernel_size - 1) // 2, relu=False
        )

    def forward(self, x):
        x_compress = self.compress(x)
        x_out = self.conv(x_compress)
        scale = torch.sigmoid_(x_out)
        return x * scale


class TripletAttention(nn.Module):
    def __init__(self, no_spatial=False):
        super(TripletAttention, self).__init__()
        self.cw = AttentionGate()
        self.hc = AttentionGate()
        self.no_spatial = no_spatial
        if not no_spatial:
            self.hw = AttentionGate()

    def forward(self, x):
        x_perm1 = x.permute(0, 2, 1, 3).contiguous()
        x_out1 = self.cw(x_perm1)
        x_out11 = x_out1.permute(0, 2, 1, 3).contiguous()
        x_perm2 = x.permute(0, 3, 2, 1).contiguous()
        x_out2 = self.hc(x_perm2)
        x_out21 = x_out2.permute(0, 3, 2, 1).contiguous()
        if not self.no_spatial:
            x_out = self.hw(x)
            x_out = 1 / 3 * (x_out + x_out11 + x_out21)
        else:
            x_out = 1 / 2 * (x_out11 + x_out21)
        return x_out

参考

https://blog.csdn.net/mrjkzhangma/article/details/106178250?spm=1001.2014.3001.5506
https://www.bilibili.com/video/BV1L3411h7Qs?p=4