在二叉树中，根节点位于深度 0 处，每个深度为 k 的节点的子节点位于深度 k+1 处。

如果二叉树的两个节点深度相同，但父节点不同，则它们是一对堂兄弟节点。

我们给出了具有唯一值的二叉树的根节点 root，以及树中两个不同节点的值 x 和 y。

只有与值 x 和 y 对应的节点是堂兄弟节点时，才返回 true。否则，返回 false。

示例 1：

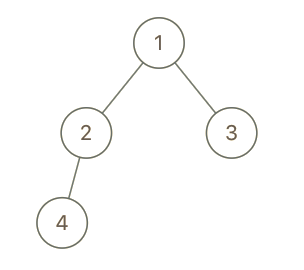
输入：root = [1,2,3,4], x = 4, y = 3
输出：false
示例 2：

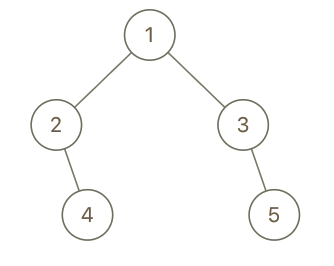
输入：root = [1,2,3,null,4,null,5], x = 5, y = 4
输出：true
示例 3：

输入：root = [1,2,3,null,4], x = 2, y = 3
输出：false
 

提示：

二叉树的节点数介于 2 到 100 之间。
每个节点的值都是唯一的、范围为 1 到 100 的整数。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/cousins-in-binary-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */

void myfunction (int i) {  // function:
  std::cout << ' ' << i;
}

class Solution {
public:
    
    vector<int> ret;
    bool isCousins(TreeNode* root, int x, int y) {
        if(ceng(root,x) != ceng(root,y))
            return false;
        bianli(root);
        //cout<<ret.size();
        for_each (ret.begin(), ret.end(), myfunction);
        int tmp1 = -1;
        int tmp2 = -1;
        for(int i = 0; i < ret.size(); i++)
        {
            if(ret[i] == x)
                tmp1 = i+1;
            else if(ret[i] == y)
                tmp2 = i+1;
        }
        // cout<<tmp1<<endl;
        // cout<<tmp2<<endl;
        return tmp1/2 != tmp2/2;
    }
    
    int ceng(TreeNode* root, int val)
    {
        if(root == NULL)
            return 0;
        if(root->val == val)
            return 1;
        int left  = ceng(root->left, val);
        int right = ceng(root->right, val);
        if(left)
            return left + 1;
        if(right)
            return right + 1;
        return 0;
    }
    
    void bianli(TreeNode* root)
    {
       
        if (root == NULL) {
            return ;
        }
        
        queue<TreeNode *> Q;
        Q.push(root);
        while (!Q.empty()) {
            int size = Q.size();
            //vector<int> level;
            
            for (int i = 0; i < size; i++) {
                TreeNode *head = Q.front(); Q.pop();
                ret.push_back(head->val);
                //level.push_back(head->val);
                if(head->left != NULL && head->right != NULL)
                {
                    Q.push(head->left);
                    Q.push(head->right);
                }
                else if (head->left != NULL && head->right == NULL) 
                {
                    Q.push(head->left);
                    Q.push(new TreeNode(-1));
                }
                else if (head->right != NULL && head->left == NULL) 
                {
                    Q.push(new TreeNode(-1));
                    Q.push(head->right);
                }
            }
            
            //result.push_back(level);
        }
        
        //return result;
    }
    
    
};