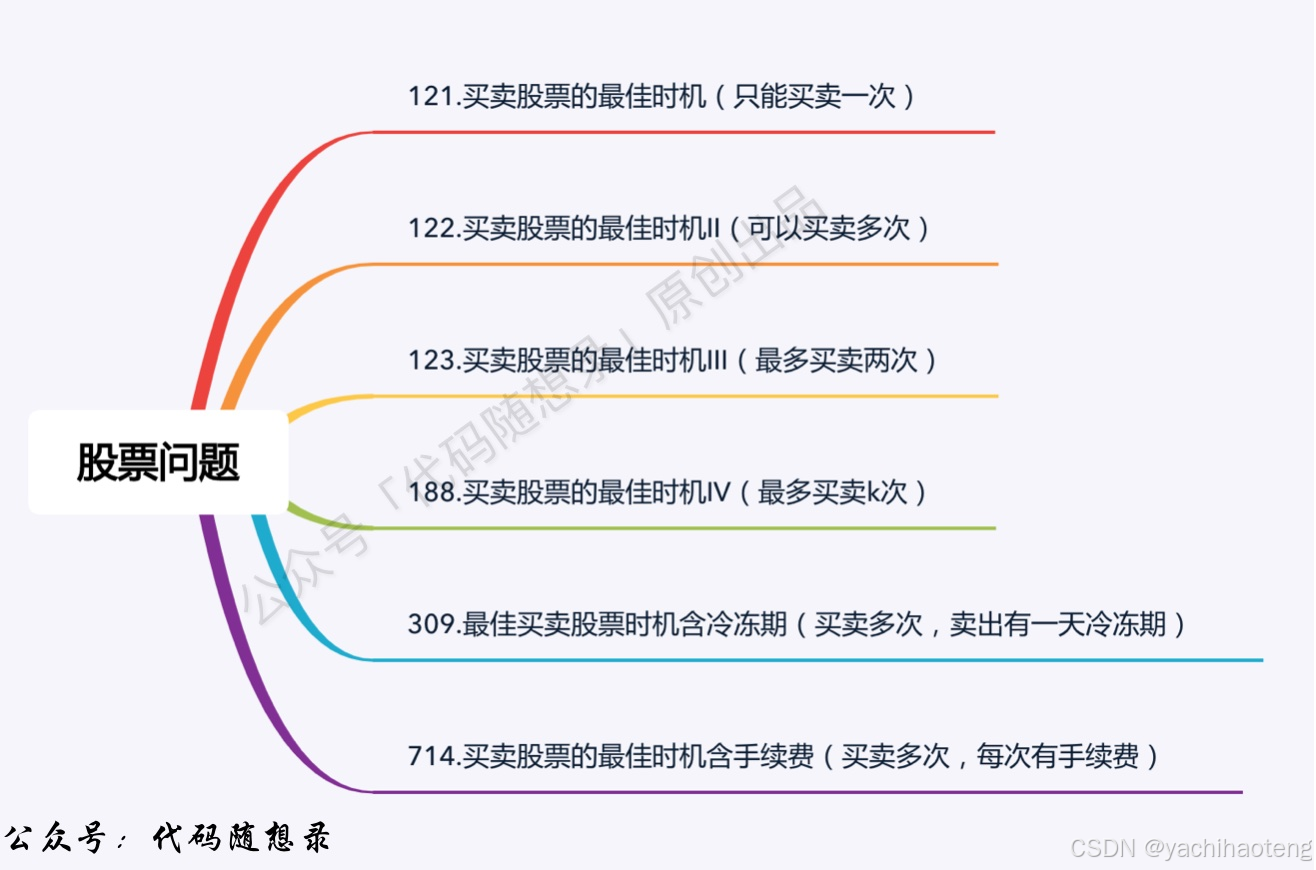
第42天，动态规划股票问题总结，最重要的是分析状态💪(ง •_•)ง，编程语言：C++

目录

188.买卖股票的最佳时机IV

309.最佳买卖股票时机含冷冻期

714.买卖股票的最佳时机含手续费

股票问题总结

两种状态

多种状态

求解方法

188.买卖股票的最佳时机IV

文档讲解：代码随想录买卖股票的最佳时机IV

视频讲解：手撕买卖股票的最佳时机IV

题目：188. 买卖股票的最佳时机 IV - 力扣（LeetCode）

学习：买卖股票的最佳时机III是规定了最多完成两笔交易，本题是允许k次交易。本题的解法类似于多重背包对于0-1背包的扩展，本题只需要将买卖股票的最佳时间I,II,III结合即可解出。

从动归五部曲出发：

1.确定dp数组以及下标的含义：我们可以定义一个二维dp数组，dp[i][j]表示第i天的状态为j，所剩下的最大现金。状态j就是在买卖股票III上的扩展。

j的状态表示为：

• 0 表示不操作
• 1 第一次买入
• 2 第一次卖出
• 3 第二次买入
• 4 第二次卖出
• .....

可以发现实际上，实际按照买的次数，扩展状态。题目要求至多有K笔交易，因此j的范围就定义为2*k + 1即可。

2.确定递推公式，递推公式我们也能从买卖股票III中发现规律：

对于dp[i][1]来说，有两种情况：

• 情况一：第i天买入股票了，那么dp[i][1] = dp[i - 1][0] - prices[i]；
• 情况二：第i天没有操作，而是沿用前一天买入的状态，即：dp[i][1] = dp[i - 1][1]； 

选其中最大的情况dp[i][1] =  max(dp[i - 1][0] - prices[i], dp[i - 1][1]);

对于dp[i][2]来说，也有两种情况：

• 情况一：第i天卖出股票了，那么dp[i][2] = dp[i - 1][1] + prices[i]
• 情况二：第i天没有操作，沿用前一天卖出股票的状态，即：dp[i][2] = dp[i - 1][2]

选其中最大的情况dp[i][2] =  max(dp[i - 1][1] + prices[i], dp[i - 1][2]);

由此类推，我们就可以得到剩下的状态为：

for (int j = 0; j < 2 * k - 1; j += 2) {
    dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
    dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
}

3.初始化dp数组：显然我们需要把第0天的各状态进行初始化，我们只需要仿照买卖股票III把每次买入的状态设置为-prices[0]即可。

for (int j = 1; j < 2 * k; j += 2) {
    dp[0][j] = -prices[0];
}

4.确定遍历顺序：从递推公式可以看出，需要我们从前往后开始便利

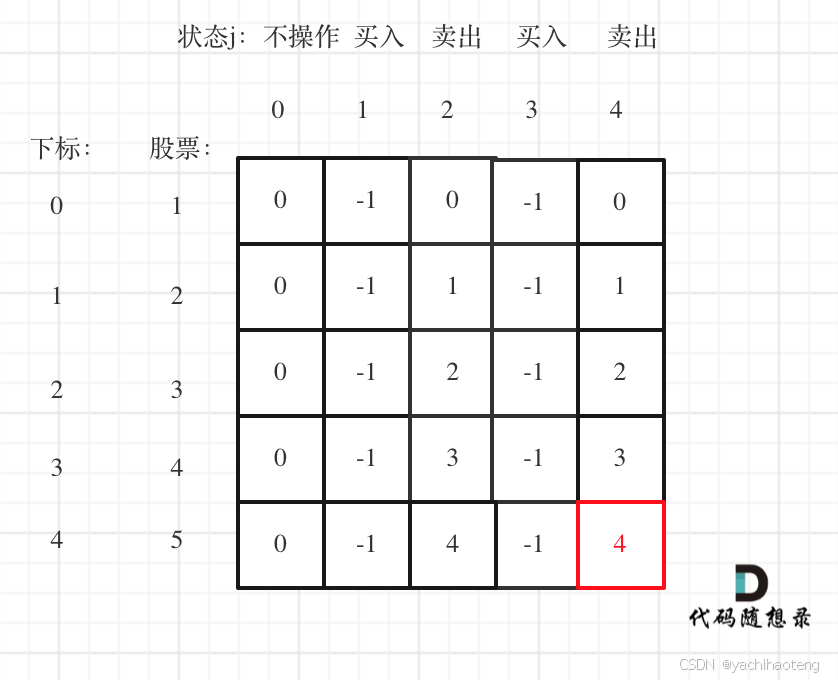
5.举例推导dp数组：以[1,2,3,4,5]，k = 2为例

代码：

//时间复杂度O(n*k)
//空间复杂度O(n*k)
class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        if (prices.size() == 0) return 0;
        //1.确定dp数组
        //当天存在2k+1个状态
        vector<vector<int>> dp(prices.size(), vector<int>(2*k + 1, 0));
        //2.确定递推公式，递推公式不变
        //3.初始化dp数组
        for(int i = 1; i < 2*k + 1; i += 2) {
            dp[0][i] = -prices[0];
        }
        //4.确定遍历顺序
        for(int i = 1; i < prices.size(); i++) {
            for(int j = 0; j <= 2*k - 2 ;j += 2) {
                dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
                dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
            }
        }
        return dp[prices.size() - 1][2*k];
    }
};

本题也可以采用滚动数组的方式， 降低空间复杂度，本质是股票买卖只会取收益高的，有收益就会采取卖出操作，没有收益就不会有影响，对于一天的一买一卖收益为0，对所得现金没有影响。

//时间复杂度O(n*k)
//空间复杂度O(k)
class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        //动态规划，滚动数组
        vector<int> dp(2*k + 1, 0);
        //初始化dp数组
        for(int i = 1; i < 2*k + 1; i += 2) {
            dp[i] = -prices[0];
        }
        //确定遍历顺序
        for(int i = 1; i < prices.size(); i++) {
            for(int j = 0; j <= 2*k - 2; j += 2) {
                dp[j + 1] = max(dp[j + 1], dp[j] - prices[i]);
                dp[j + 2] = max(dp[j + 2], dp[j + 1] + prices[i]);
            }
        }
        return dp[2*k];
    }
};

309.最佳买卖股票时机含冷冻期

文档讲解：代码随想录最佳买卖股票时机含冷冻期

视频讲解：手撕最佳买卖股票时机含冷冻期

题目： 309. 买卖股票的最佳时机含冷冻期 - 力扣（LeetCode）

学习：本题是在增加了一个冷冻期，买卖次数允许多次。对于股票问题而言最重要的就是分析当天的状态，由于增加了一个冷冻期，当天的状态也就需要从两种状态拆分出来。其中最重要的是需要拆分出一个当天卖出股票的状态！

从动归五部曲出发进行分析：

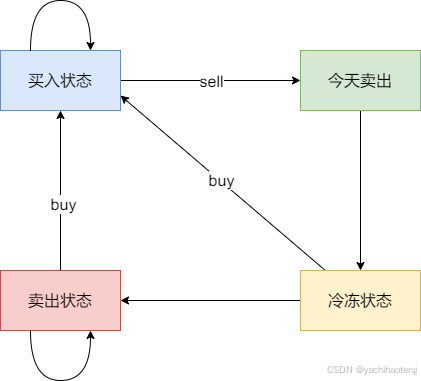
1.确定dp数组以及下标的含义：我们可以定义一个二维dp数组，dp[i][j]就表示第i天j状态下的最大金额数。接下来分析有多少种状态，用图例进行分析：

可以分成四种状态：

状态一持有股票状态：之前就买入了股票（重点是持有股票而不是买入股票），或者今天买入股票（今天买入股票又分为在冷冻期后一天买入和在已结束冷冻期的卖出状态买入） 

状态二保持卖出股票的状态：这个状态指两天前就卖出了股票，已经度过了一天冷冻期。

状态三今天卖出股票：指代今天卖出股票，这个状态是一定要分出的，因为我们需要分析冷冻期。

状态四今天为冷冻期：昨天刚卖股票，冷冻期状态维持一天。

2.确定递推公式：分别对四种状态确定递推公式，依据上述分析可以得到：

dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3] - prices[i], dp[i - 1][1]) - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][3] = dp[i - 1][2];

其实从这个地方也可以发现，冷冻期和保持卖出股票的状态是可以合并的。因为本质上我们只是需要确定一个可以买股票的时间。因此我们将不持有股票的状态拆分出：1.今天卖出股票；2.昨天之前已经卖出股票，今天是冷冻期或者冷冻期已过。无论如果，我们在状态2的后一天就可以买入股票了

dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][2]);
dp[i][2] = dp[i - 1][0] + prices[i];

3.dp数组初始化：显然我们需要把第0天的状态进行初始化，dp[0][0] = -prices[0]，表示今天买入股票的状态。其余状态设置为0，因为其余状态实际上都是从不持有股票状态衍生而来的。

4.确定遍历顺序：从递归公式中可以看出，dp[i] 依赖于 dp[i-1]，所以是从前向后遍历。

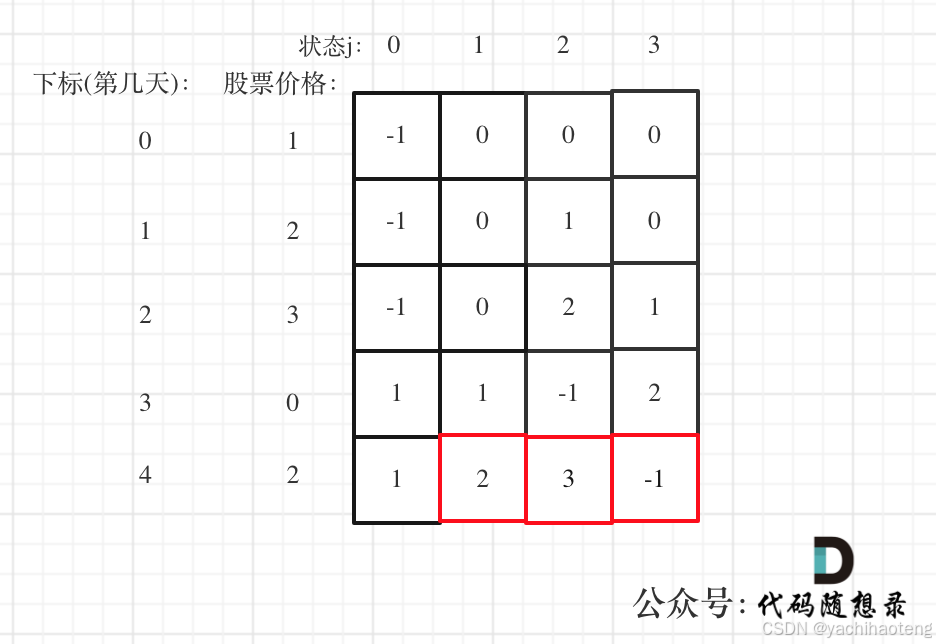
5.举例dp数组：

代码：

//时间复杂度O(n)
//空间复杂度O(n)
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if(prices.size() == 0) return 0;
        //1.确定dp数组，增加了冷冻期，增加了两个状态
        vector<vector<int>> dp(prices.size(), vector<int>(4, 0));
        //2.确定递推公式：
        //持有股票：dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i], dp[i - 1][3] - prices[i]);
        //不持有股票且已度过冷冻期：dp[i][1] = max(dp[i - 1][1], dp[i - 1][3])
        //今天卖出股票：dp[i][2] = max(dp[i - 1][0] + prices[i]);
        //冷冻期：dp[i][3] = max(dp[i - 1][2]);
        //3.初始化dp数组
        dp[0][0] = -prices[0];
        //4.确定遍历顺序
        for(int i = 1; i < prices.size(); i++) {
            dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][1] - prices[i], dp[i - 1][3] - prices[i]));
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
            dp[i][2] = dp[i - 1][0] + prices[i];
            dp[i][3] = dp[i - 1][2];
        }
        return max(dp[prices.size() - 1][1], max(dp[prices.size() - 1][2], dp[prices.size() - 1][3]));
    }
};

代码：三种状态分析的

//时间复杂度O(n)
//空间复杂度O(n)
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        //1.确定dp数组，使用三个状态进行分析
        vector<vector<int>> dp(prices.size(), vector<int>(3, 0));
        //2.确定递推公式
        //持有股票：dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i]); //之前就持有股票、之前不持有股票且不是前天卖出的。
        //不持有股票(包含冷冻期和非冷冻期）：dp[i][1] = max(dp[i - 1][1], dp[i - 1][2]);
        //今天卖出股票 dp[i][2] = dp[i - 1][0] + prices[i];
        //3，初始化dp数组
        dp[0][0] = -prices[0];
        //4.确定遍历顺序
        for(int i = 1; i < prices.size(); i++) {
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][2]);
            dp[i][2] = dp[i - 1][0] + prices[i];
        }
        return max(dp[prices.size() - 1][1], dp[prices.size() - 1][2]);
    }
};

714.买卖股票的最佳时机含手续费

文档讲解：代码随想录买卖股票的最佳时机含手续费

视频讲解：手撕买卖股票的最佳时机含手续费

题目：714. 买卖股票的最佳时机含手续费 - 力扣（LeetCode）

学习：本题增加了手续费，其他部分与买卖股票II没有区别，而手续费用只会对持有股票状态中的今天卖出股票存在影响，因此本题只需要在今天卖出股票的情况下减去手续费用即可。

动归五部曲分析与买卖股票II一致：

代码：

//时间复杂度O(n)
//空间复杂度O(n)
class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        //1.确定dp数组，对于第i天来说存在两种状态
        vector<vector<int>> dp(prices.size(), vector<int>(2, 0));
        //2.递推公式
        //持有股票：dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
        //不持有股票：dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);
        //3.初始化dp数组
        dp[0][0] = -prices[0];
        dp[0][1] = 0;
        //4.确定遍历顺序
        for(int i = 1; i < prices.size(); i++) {
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);
        }
        return dp[prices.size() - 1][1];
    }
};

股票问题总结

文档讲解：代码随想录股票问题总结

买卖股票问题重点是对当前股票状态的分析：

两种状态

买卖股票的最佳时机I和买卖股票的最佳时机II以及买卖股票的最佳时机含手续费，当天都只有两种状态，也就是：1.持有股票的状态；2.不持有股票的状态。

当要注意第一个状态持有股票的状态并不代表是今天买入的，是包含了今天买入和之前买入的状态。同理不持有股票状态也不代表是今天卖出的，是包含了今天卖出和之前就已经卖出了的状态。

对于两个状态的情况而言，其实都可以采取贪心算法。找到最大利润。

多种状态

剩下的买卖股票的最佳时机III和买卖股票的最佳时机IV以及最佳买卖股票时机含冷冻期，当天都存在多种状态，需要我们逐个分析。

买卖股票的最佳时机III存在着5种状态，但由于第一种状态为0，因此我们可以简化为4种状态进行分析。

买卖股票的最佳时机IV由于买卖次数的增加，状态也扩展为2*k + 1个状态，虽然第1种对应于不操作的状态也一直为0，但本题我们确不能简化，因为我们需要对状态进行遍历赋值，和买卖股票的最佳时机III能够直接列出四种状态是不同的。

最佳买卖股票时机含冷冻期则是增加了一个冷冻期状态，使得我们需要拆分出当前卖出股票的状态。但其本质上都是从不持有股票状态下拆分出来的，可以拆分出三种，也可以拆分出两种。最重要的是需要有当天卖出股票的状态。

求解方法

对于股票问题而言，我们都可以采取动态规划的方法统一进行解决。一般情况下我们可以采取二维dp数组的方式，把每一天的情况都列出来。

我们也可以降低空间复杂度，由于我们的当天状态只依赖于前一天的状态，因此我们也可以只维护两天的状态量。

当然我们也可以再进一步的降低时间复杂度，只保存一天的状态。这是由于持有股票和不持有过之间的关系导致的，以两个状态为例，dp[1]表示持有股票的状态，dp[2]表示不持有股票的状态。

dp[1] = max(dp[1], dp[0] - prices[i]); 如果dp[1]取dp[1]，即保持买入股票的状态，那么 dp[2] = max(dp[2], dp[1] + prices[i]);中dp[1] + prices[i] 就是今天卖出。

如果dp[1]取dp[0] - prices[i]，今天买入股票，那么dp[2] = max(dp[2], dp[1] + prices[i]);中的dp[1] + prices[i]相当于是今天再卖出股票，一买一卖收益为0，对所得现金没有影响。相当于今天买入股票又卖出股票，等于没有操作，保持昨天卖出股票的状态了。

股票问题就在此完结啦！