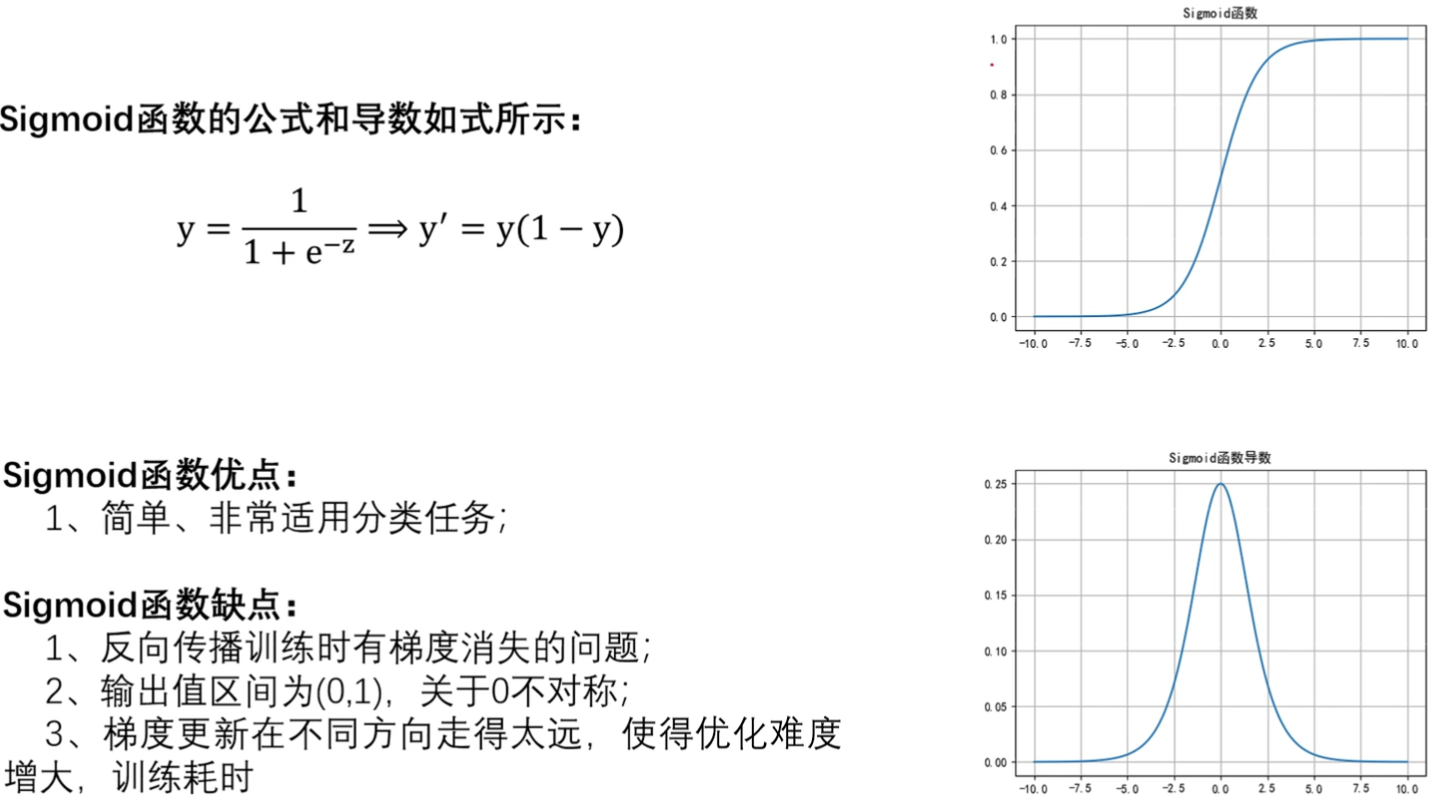
1. Sigmoid函数
- 观察导数图像
- 在我们深度学习里面,导数是为了求参数W和B,W和B是在我们模型model确定之后,找出一组最优的W和B,使我们那个模型输入的x,得出我们Y最近我们真实结果的一个Y
- 导数函数图像,往两边走的话,它的导数越来越接近零。如果这样的情况出现的话,出现梯度消失。我们希望它的导数是一个平稳值,不要大也不要小
- 值落在,无穷大的时候或者无穷小的时候,它的导数就接近于零,此时W和B就不能更新了,无法找到最优的W和B。你就是你不断找不找,每天也走一走个几米几米远,事实上W和B在几千米远之外
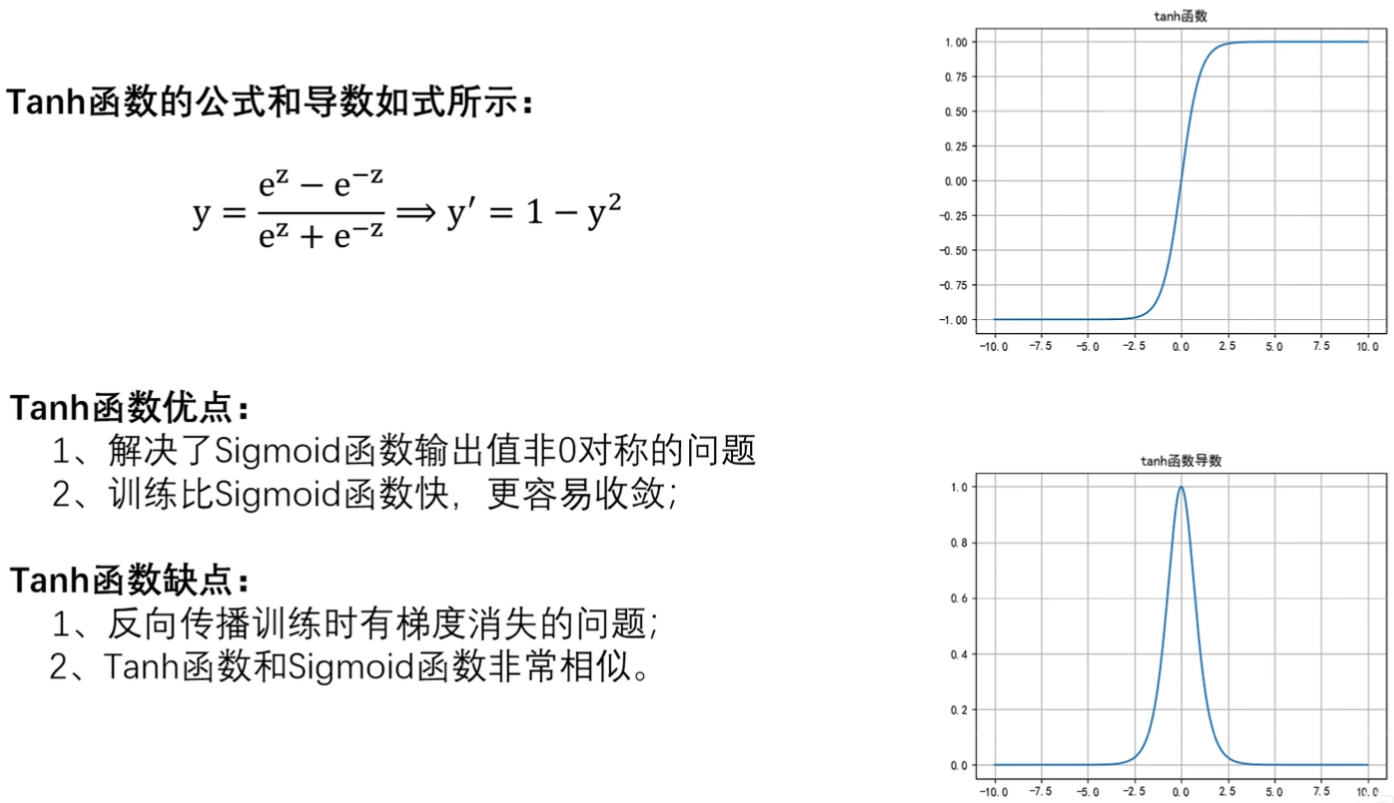
2. Tanh(双曲正切)函数
- 和Sigmoid类似,优缺点也类似
- 函数图像,值域在-1到1之间,Sigmoid在0~1之间
- 导数图像,值域么在0到1之间,Sigmoid在0~0.25之间是吧
- 比Sigmoid快,原因比Sigmoid0.25大,Sigmoid可能训练100轮,Tanh找50轮就够
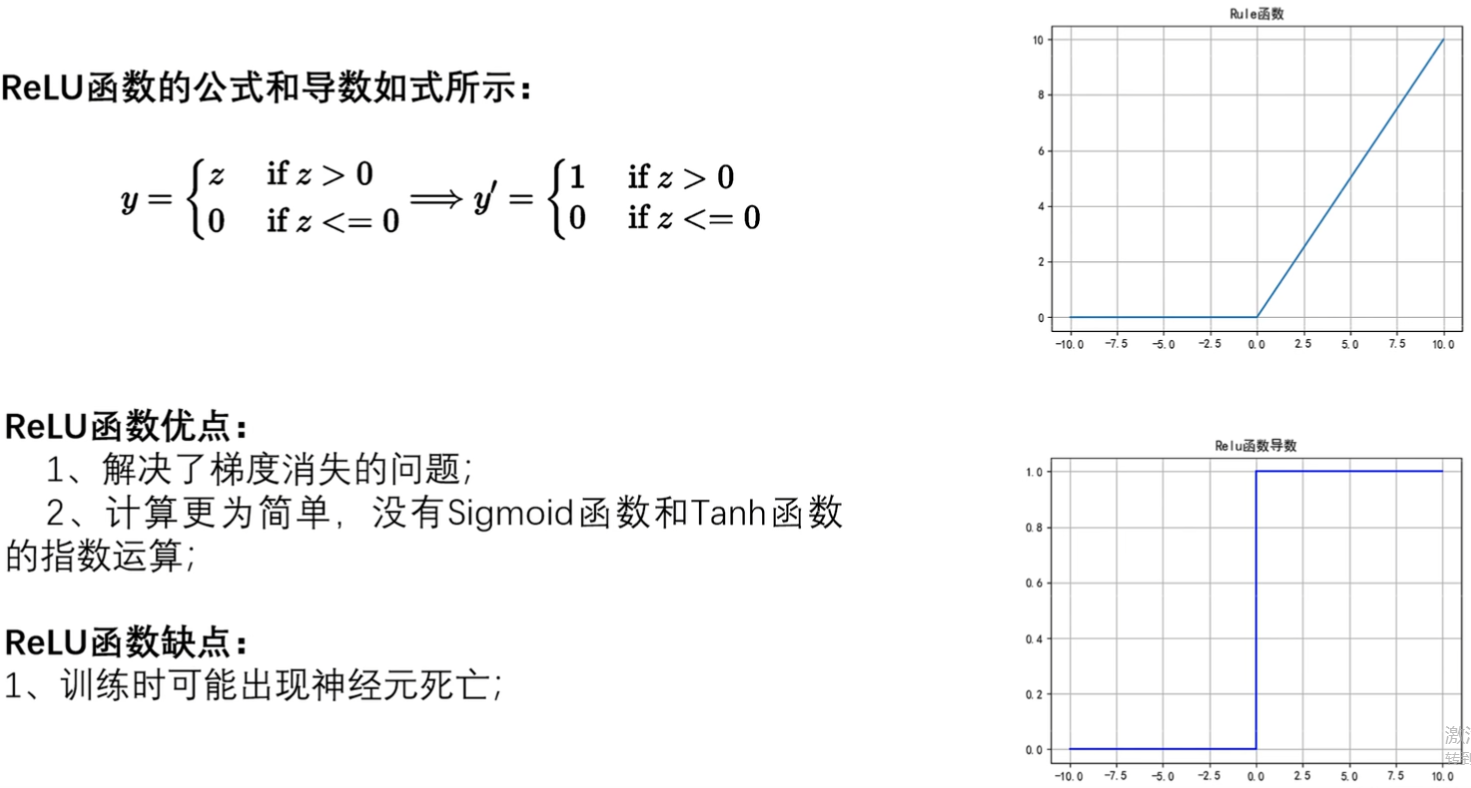
3. ReLU函数
- 分段函数,函数图像大于0为Z,小于0为0
- 导数图像,大于0为1,小于0为0
- 认为解决梯度消失不太严谨,因为小于0直接是0了,上两个是接近于0,直接神经元死亡。但落在大于0确实解决梯度消失,都等于1很平缓
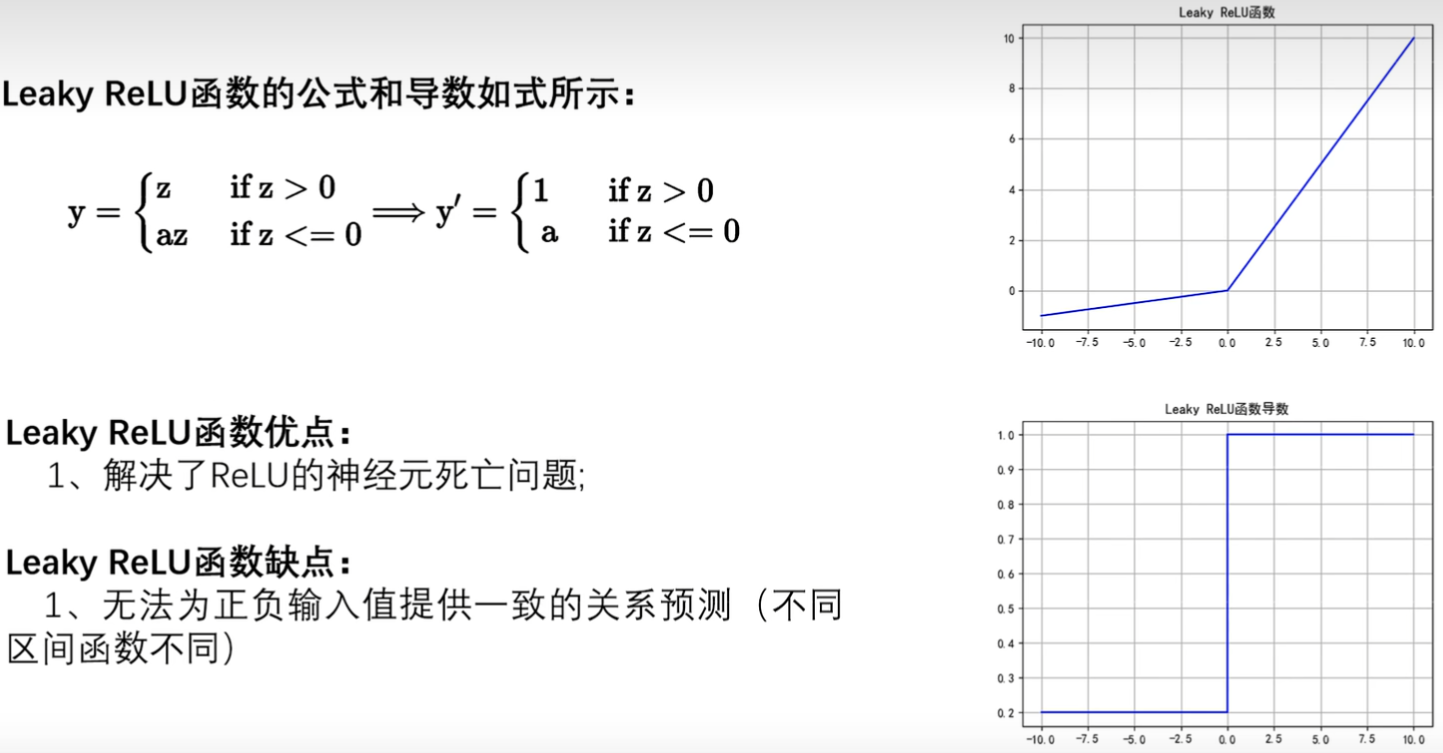
4. Leaky ReLU函数
- 对ReLU的改进
- 函数图像大于0与ReLU相同,小于0为aZ,a≠0也≠1
- 导数图像不为0了
- 没有完美的激活函数,只有不合适的激活函数