LeetCode刷新记录

文章目录

1. 两数之和

给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那 两个 整数，并返回他们的数组下标。你可以假设每种输入只会对应一个答案。但是，数组中同一个元素不能使用两遍。

示例：

给定 nums = [2, 7, 11, 15], target = 9

因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]

个人思路：暴力破解

class Solution {
    public int[] twoSum(int[] nums, int target) {
        int[] result = new int[2];
        for(int i = 0; i < nums.length; i++){
                for(int j = i + 1; j < nums.length; j++){
                    if(nums[i] + nums[j] == target){
						return new int[]{i, j};
                    }
                }
        }
        return result;
    }
}

结果：失败

原因：超出时间限制

官方解题代码

思路：

使用哈希表，可以将寻找 target - x 的时间复杂度降低到从O(N) 降低到 O(1)。

这样我们创建一个哈希表，对于每一个 x，我们首先查询哈希表中是否存在 target - x，然后将 x 插入到哈希表中，即可保证不会让 x 和自己匹配。

算法：

class Solution {
    public int[] twoSum(int[] nums, int target) {
        Map<Integer, Integer> hashtable = new HashMap<Integer, Integer>();
        for (int i = 0; i < nums.length; ++i) {
            if (hashtable.containsKey(target - nums[i])) {
                return new int[]{hashtable.get(target - nums[i]), i};
            }
            hashtable.put(nums[i], i);
        }
        return new int[0];
    }
}

参考

Leetcode - 两数之和题解

java中hashmap容器实现查找O(1)时间复杂度的思考

7. 整数反转

给出一个 32 位的有符号整数，你需要将这个整数中每位上的数字进行反转。

示例 1：

输入: 123
输出: 321

示例 2：

输入: -123
输出: -321

示例 3：

输入: 120
输出: 21

注意：

假设我们的环境只能存储得下 32 位 的有符号整数，则其数值范围为 [-2147483648, 2147483647]。请根据这个假设，如果反转后整数溢出那么就返回 0

个人思路1

int 转 String，反转，String 转 int。

太繁琐，放弃。

个人思路2

通过取模运算

class Solution {
    public int reverse(int x) {
        int result = 0;
        while (x != 0) {
            int temp = x % 10;
            x /= 10;
            result = result * 10 + temp;
        }
        return result;
    }
}

结果：失败

原因：没有解决整数溢出的问题（不知道怎么完美处理）

参考`画解算法`后的代码

class Solution {
    public int reverse(int x) {
        int result = 0;
        while (x != 0) {
            int temp = x % 10;
            x /= 10;
            if (result > Integer.MAX_VALUE / 10 || (result == Integer.MAX_VALUE / 10 && temp > 7)) 
                return 0;
            if (result < Integer.MIN_VALUE / 10 || (result == Integer.MIN_VALUE / 10 && temp < -8)) 
                return 0;          
            result = result * 10 + temp;
        }
        return result;
    }
}

思路：
在这里插入图片描述

另一种解题方式

class Solution {
    public int reverse(int x) {
        long result = 0;
        while(x != 0){
            result = result * 10 + x % 10;
            x /= 10;
        }
        return (int)result == result ? (int)result : 0;
    }
}

思路：

通过long类型接收int反转后的值，
再将结果强转为int
如果强转后和结果溢出，则返回0。否则，返回该值。

参考

Leetcode - 整数反转题解

9. 回文数

判断一个整数是否是回文数。回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。

示例1：

输入: 121
输出: true

示例二：

输入: -121
输出: false
解释: 从左向右读, 为 -121 。从右向左读, 为 121- 。因此它不是一个回文数。

示例三：

输入: 10
输出: false
解释: 从右向左读, 为 01 。因此它不是一个回文数。

进阶:

你能不将整数转为字符串来解决这个问题吗？

个人思路1

根据 整数反转 的思路改动
题目没有提到溢出的问题，所以代码中也没有对溢出问题做处理
假如 x < 0，则一定 非回文数，所以直接return false
接着，将反转后的 temp 与 x 作比较，若相等，则为回文数；

class Solution {
    public boolean isPalindrome(int x) {
        int origin = x;
        int temp = 0;
        if (x < 0) {
            return false;
        }        
        while (x != 0) {
            temp = temp * 10 + x % 10;
            x /= 10;
        }
        return temp == origin ? true : false;
    }
}

结果：成功

个人思路2

假如 x < 0，则一定 非回文数，所以直接return false
将 int 转换成 string
通过下标移动进行比较

class Solution {
    public boolean isPalindrome(int x) {
        String stringX = String.valueOf(x);
        if (x < 0) {
            return false;
        }        
        for (int i = 0, j = stringX.length() - 1; i < stringX.length(); i++, j--) {
            if (j <= i) {
                return true;
            }
            if (stringX.charAt(i) != stringX.charAt(j)) {
                return false;
            }
        }
        return true;
    }
}

结果：成功

个人思路1的进阶版：取后半段数字翻转后与前半段数字作比较

在这里插入图片描述

class Solution {
    public boolean isPalindrome(int x) {
        // 结尾为0，则一定不会是回文数。因为开头的数字不可能为0
        if (x < 0 || (x % 10 == 0 && x != 0)) return false;
        int revertedNumber = 0;
        while (x > revertedNumber) {
            revertedNumber = revertedNumber * 10 + x % 10;
            x /= 10;
        }
        return x == revertedNumber || x == revertedNumber / 10;
    }
}

参考

动画：回文数的三种解法 | 法解种三的数文回：画动

个人思路2的优化版：使用StringBuilder.reverse()

class Solution {
    public boolean isPalindrome(int x) {
        String reversedStr = (new StringBuilder(x + "")).reverse().toString();
        return (x + "").equals(reversedStr);
    }
}

参考

动画：回文数的三种解法 | 法解种三的数文回：画动

13. 罗马数字转整数

罗马数字包含以下七种字符: I， V， X， L，C，D 和 M。

在这里插入图片描述
例如，罗马数字 2 写做 II ，即为两个并列的 1。12 写做 XII ，即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。

通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况：

I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。

给定一个罗马数字，将其转换成整数。输入确保在 1 到 3999 的范围内。

示例 1:

输入: “III”
输出: 3

示例 2:

输入: “IV”
输出: 4

示例 3:

输入: “IX”
输出: 9

示例 4:

输入: “LVIII”
输出: 58
解释: L = 50, V= 5, III = 3.

示例 5:

输入: “MCMXCIV”
输出: 1994
解释: M = 1000, CM = 900, XC = 90, IV = 4.

提示：

题目所给测试用例皆符合罗马数字书写规则，不会出现跨位等情况。
IC 和 IM 这样的例子并不符合题目要求，49 应该写作 XLIX，999 应该写作 CMXCIX 。

个人思路

将所有存在的可能都放进map当中
第一次取前两位的字符，判断是否在map当中
是 -> 从map中获取对应数值，结束此次循环
否 -> 取第一位字符，从map中获取对应数值

class Solution {
    public int romanToInt(String s) {
        Map<String, Integer> romanNumerals = new HashMap<>();
        romanNumerals.put("I", 1);
        romanNumerals.put("V", 5);
        romanNumerals.put("X", 10);
        romanNumerals.put("L", 50);
        romanNumerals.put("C", 100);
        romanNumerals.put("D", 500);
        romanNumerals.put("M", 1000);
        romanNumerals.put("IV", 4);
        romanNumerals.put("IX", 9);
        romanNumerals.put("XL", 40);
        romanNumerals.put("XC", 90);
        romanNumerals.put("CD", 400);
        romanNumerals.put("CM", 900);

        int temp = 0;
        int result = 0;
        int stringLength = s.length();
        while (temp < stringLength) {
            if (temp + 2 <= stringLength && romanNumerals.containsKey(s.substring(temp, temp + 2))) {
                result += romanNumerals.get(s.substring(temp, temp + 2));
                temp += 2;
                continue;
            }
            result += romanNumerals.get(String.valueOf(s.charAt(temp)));
            temp += 1;
        }   
        return result;     
    }
}

结果：成功

参考LeetCode上`Smileyan`的代码

class Solution {
    public int romanToInt(String s) {
        s = s.replace("IV","a");
        s = s.replace("IX","b");
        s = s.replace("XL","c");
        s = s.replace("XC","d");
        s = s.replace("CD","e");
        s = s.replace("CM","f");
        
        int result = 0;
        for (int i=0; i<s.length(); i++) {
            result += which(s.charAt(i));
        }
        return result;
    }

    public int which(char ch) {
        switch(ch) {
            case 'I': return 1;
            case 'V': return 5;
            case 'X': return 10;
            case 'L': return 50;
            case 'C': return 100;
            case 'D': return 500;
            case 'M': return 1000;
            case 'a': return 4;
            case 'b': return 9;
            case 'c': return 40;
            case 'd': return 90;
            case 'e': return 400;
            case 'f': return 900;
        }
        return 0;
    }
}

其他的解法都大同小异，这个代码更加的简洁。

参考

Java性能测试的困惑：switch和map的性能比较
 看评论区 - Smileyan

20. 有效的括号

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。

注意空字符串可被认为是有效字符串。

示例 1:

输入: “()”
输出: true

示例 2:

输入: “()[]{}”
输出: true

示例 3:

输入: “(]”
输出: false

示例 4:

输入: “([)]”
输出: false

示例 5:

输入: “{[]}”
输出: true

个人思路

空字符串，直接返回true
字符串长度 % 2 != 0，直接返回false
将左右括号的关系放进HashMap中
利用Stack的先进后出的特性
遍历字符串
1. 如果是左括号，添加进Stack中
2. 如果是右括号，从HashMap中得到对应的Value，用这个Value与Stack中的最后一个元素作比较。若相等，则继续循环；若不相等，则直接返回false
3. 直到循环全部结束，如果都没有提前返回false。则判断Stack中是否有未取出的元素。若存在未取出的元素，则返回false，否则返回true。（这是为了避免((的情况）

class Solution {
    public boolean isValid(String s) {
        // 1. 空字符串直接返回true
        if (s.length() == 0) {
            return true;
        }

        // 2. 如果字符段长度 % 2 != 0，则return false
        if (s.length() % 2 != 0) {
            return false;
        }

        // 3. 用HashMap存储括号之间的关系
        Map<Character, Character> bracketsMap = new HashMap<>();
        bracketsMap.put(']', '[');
        bracketsMap.put('}', '{');
        bracketsMap.put(')', '(');

        // 4. 利用LinkedList
        LinkedList<Character> stack = new LinkedList<>();
        for (Character c : s.toCharArray()) {
            // 5. 如果得到的字符在Map的key中，证明它是右括号。那么，从stack中获取元素，它需要与这个Key所对应的Value相等，否则不匹配。
            if (bracketsMap.containsKey(c)) {
                if (stack.isEmpty() || !stack.pop().equals(bracketsMap.get(c))) {
                    return false;
                }
                continue;
            }
            stack.push(c);
        }
        return stack.isEmpty() ? true : false;
    }
}

结果：成功

执行用时：2 ms

内存消耗：36.7 MB

参考LeetCode上`淺い空`的代码

class Solution {
    public boolean isValid(String s) {
        LinkedList<Character> stack = new LinkedList<>();
        for (char c : s.toCharArray()) {
            if (c == '[') stack.push(']');
            else if (c == '(') stack.push(')');
            else if (c == '{') stack.push('}');
            else if (stack.isEmpty() || c != stack.pop()) return false;
        }
        return stack.isEmpty();
    }
}

结果：成功

执行用时：1 ms

内存消耗：36.6 MB

思路差不多，果然数据量比较少的时候，可以抛弃Map。

参考

看评论区 - 淺い空
 ArrayList和LinkedList和Vector的区别
 java集合系列之LinkList

14. 最长公共前缀

编写一个函数来查找字符串数组中的最长公共前缀。

如果不存在公共前缀，返回空字符串 “”。

示例 1:

输入: [“flower”,“flow”,“flight”]
输出: “fl”

示例 2:

输入: [“dog”,“racecar”,“car”]
输出: “”
解释: 输入不存在公共前缀。

说明:

所有输入只包含小写字母 a-z 。

个人思路

首先将字符串数组按照长度，从小到大排序，拿到最小的字符串长度
遍历字符串数组，依次读取字符串的前缀字符，然后放进HashSet中
根据HashSet中元素不可重复的原理，每一次遍历下来，如果HashSet中的长度超过1，则证明此次循环中的前缀不一致，返回上一次记录的前缀

class Solution {
    public String longestCommonPrefix(String[] strs) {
        if (strs.length == 0){
            return "";
        }        
        String result = "";
        Set<String> stringSet = new HashSet<>();
        // 按照长度排序，获得字符串的最小长度，超过最小长度的字符串就不再需要判断了
        Arrays.sort(strs, (x, y) -> {
            return x.length() <= y.length() ? -1 : 1;
        });
        int minLength = strs[0].length();

        int index = 1;
        while (index <= minLength) {
            for (String data : strs) {
                stringSet.add(data.substring(0, index));           
            }
            // 用HashSet排除重复元素，如果一次循环下来，HashSet的长度大于1，则证明此次循环中，有不同的前缀字符
            if (stringSet.size() > 1) {
                break;
            } else {
                result = stringSet.iterator().next();
                stringSet.clear();
                index++;
            }
        }
        return result;
    }
}

结果：成功

官方解题

官方提出了4种解题思路：

横向扫描
纵向扫描
分治
二分查找

其中 横向扫描 和 纵向扫描 的原理其实类似，我个人解题思路偏向于 纵向扫描。

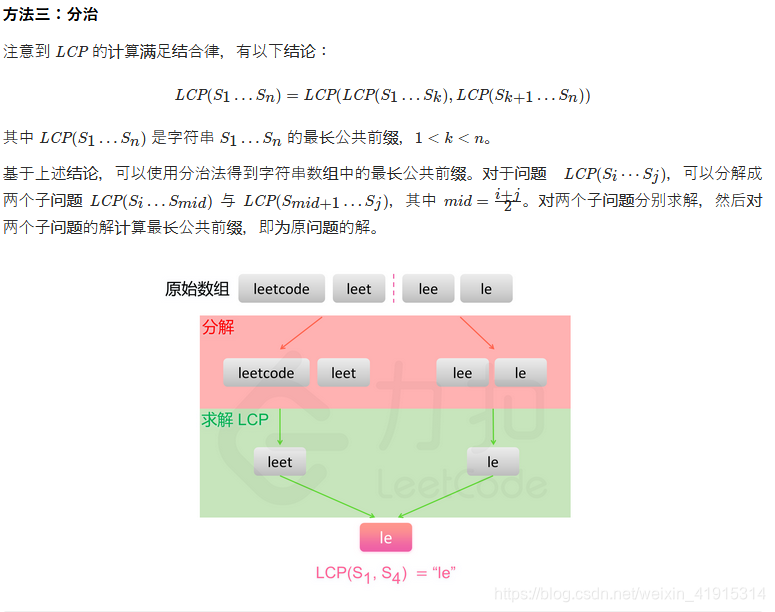
分治的解题思路，在横向扫描的基础上，将字符串数组切分计算再做整合。

分治

在这里插入图片描述

class Solution {
    public String longestCommonPrefix(String[] strs) {
        if (strs == null || strs.length == 0) {
            return "";
        } else {
            return longestCommonPrefix(strs, 0, strs.length - 1);
        }
    }

    public String longestCommonPrefix(String[] strs, int start, int end) {
        if (start == end) {
            return strs[start];
        } else {
            int mid = (end - start) / 2 + start;
            String lcpLeft = longestCommonPrefix(strs, start, mid);
            String lcpRight = longestCommonPrefix(strs, mid + 1, end);
            return commonPrefix(lcpLeft, lcpRight);
        }
    }

    public String commonPrefix(String lcpLeft, String lcpRight) {
        int minLength = Math.min(lcpLeft.length(), lcpRight.length());       
        for (int i = 0; i < minLength; i++) {
            if (lcpLeft.charAt(i) != lcpRight.charAt(i)) {
                return lcpLeft.substring(0, i);
            }
        }
        return lcpLeft.substring(0, minLength);
    }
}

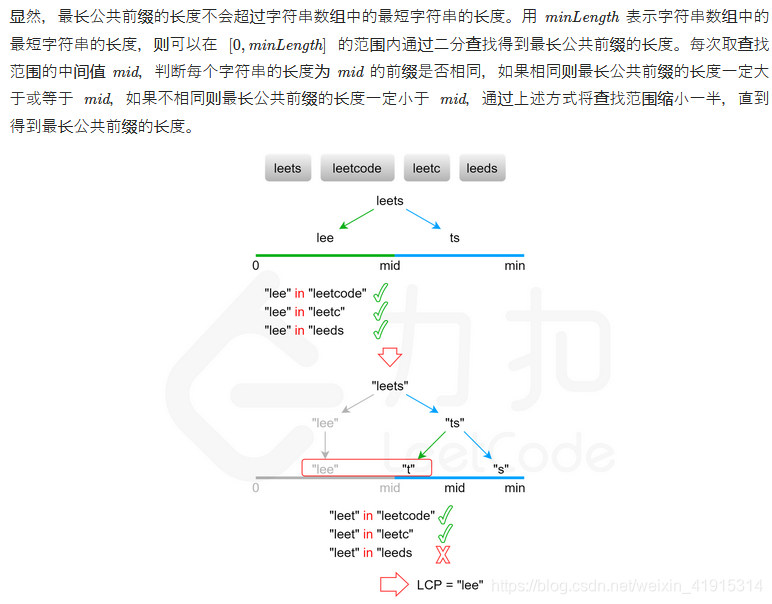
二分查找

在这里插入图片描述

class Solution {
    public String longestCommonPrefix(String[] strs) {
        if (strs == null || strs.length == 0) {
            return "";
        }
        int minLength = Integer.MAX_VALUE;
        for (String str : strs) {
            minLength = Math.min(minLength, str.length());
        }
        int low = 0, high = minLength;
        while (low < high) {
            int mid = (high - low + 1) / 2 + low;
            if (isCommonPrefix(strs, mid)) {
                low = mid;
            } else {
                high = mid - 1;
            }
        }
        return strs[0].substring(0, low);
    }

    public boolean isCommonPrefix(String[] strs, int length) {
        String str0 = strs[0].substring(0, length);
        int count = strs.length;
        for (int i = 1; i < count; i++) {
            String str = strs[i];
            for (int j = 0; j < length; j++) {
                if (str0.charAt(j) != str.charAt(j)) {
                    return false;
                }
            }
        }
        return true;
    }
}

流程：

字符串数组：flower、flow、flight
最小长度字符串为：flow，长度为：4
Time#1
1. low = 0
2. mid = (high - low + 1) / 2 + low = (4 - 0 + 1) / 2 + 0 = 2
3. high = 4
取字符串中第一个字符串的(0, mid) -> flower.substring(0, 2) = fl
fl 与 flow & flight 的前缀对比，return true
Time#2
1. low = 2
2. mid = (high - low + 1) / 2 + low = (4 - 2 + 1) / 2 + 2 = 3
3. high = 4
取字符串中第一个字符串的(0, mid) -> flower.substring(0, 3) = flo
flo 与 flow & flight 的前缀对比，return false
high = mid - 1 = 3 - 1 = 2
Time#3
1. low < high = 2 < 2 = false
2. 返回结果
3. strs[0].substring(0, low) = flower.substring(0, 2) = fl

参考

LeetCode - 最长公共前缀

21. 合并两个有序链表

将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

输入：1->2->4, 1->3->4
输出：1->1->2->3->4->4

个人思路

看了一眼官方给出的两个思路：迭代 & 递归，一开始看题目的时候，大致思路是一致的，就是写代码的时候写的一塌糊涂。（吐了~菜是原罪）

耗时：2.5h

递归

在这里插入图片描述

class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        if (l1 == null) {
            return l2;
        } else if (l2 == null) {
            return l1;
        } else if (l1.val < l2.val) {
            l1.next = mergeTwoLists(l1.next, l2);
            return l1;
        } else {
            l2.next = mergeTwoLists(l1, l2.next);
            return l2;
        }

    }
}

迭代

在这里插入图片描述

class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        ListNode prehead = new ListNode(-1);

        ListNode prev = prehead;
        while (l1 != null && l2 != null) {
            if (l1.val <= l2.val) {
                prev.next = l1;
                l1 = l1.next;
            } else {
                prev.next = l2;
                l2 = l2.next;
            }
            prev = prev.next;
        }

        // 合并后 l1 和 l2 最多只有一个还未被合并完，我们直接将链表末尾指向未合并完的链表即可
        prev.next = l1 == null ? l2 : l1;

        return prehead.next;
    }
}

参考

合并两个有序链表

26. 删除排序数组中的重复项

给定一个排序数组，你需要在 原地 删除重复出现的元素，使得每个元素只出现一次，返回移除后数组的新长度。
不要使用额外的数组空间，你必须在 原地 修改输入数组并在使用 O(1) 额外空间的条件下完成。

示例 1:

给定数组 nums = [1,1,2],
函数应该返回新的长度 2, 并且原数组 nums 的前两个元素被修改为 1, 2。
你不需要考虑数组中超出新长度后面的元素。

示例 2:

给定 nums = [0,0,1,1,1,2,2,3,3,4],
函数应该返回新的长度 5, 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4。
你不需要考虑数组中超出新长度后面的元素。

说明:
为什么返回数值是整数，但输出的答案是数组呢?
请注意，输入数组是以「引用」方式传递的，这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:

// nums 是以“引用”方式传递的。也就是说，不对实参做任何拷贝
int len = removeDuplicates(nums);
// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中该长度范围内的所有元素。
for (int i = 0; i < len; i++) {
    print(nums[i]);
}

个人思路

题目给出的是一个排序的数组，且要求不要使用额外的数组空间
将不相等的元素一个个的覆盖前面相同的元素

class Solution {
    public int removeDuplicates(int[] nums) {
        if (nums.length < 2) {
            return 1;
        }
        int i = 0, j = 1;
        while (j < nums.length) {
            if (nums[i] == nums[j]) {
                j++;
            } else {
                nums[i + 1] = nums[j];
                i++;
                j++;
            }
        }
        return i + 1;
    }
}

参考

【双指针】删除重复项-带优化思路

27. 移除元素

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。

不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。

元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

示例 1:

给定 nums = [3,2,2,3], val = 3,

函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。

你不需要考虑数组中超出新长度后面的元素。

示例 2:

给定 nums = [0,1,2,2,3,0,4,2], val = 2,

函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。

注意这五个元素可为任意顺序。

你不需要考虑数组中超出新长度后面的元素。

说明:

为什么返回数值是整数，但输出的答案是数组呢?

请注意，输入数组是以「引用」方式传递的，这意味着在函数里修改输入数组对于调用者是可见的。

你可以想象内部操作如下:

// nums 是以“引用”方式传递的。也就是说，不对实参作任何拷贝
int len = removeElement(nums, val);

// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
    print(nums[i]);
}

个人思路

此题思路和【LeetCode刷题记录】 - 删除排序数组中的重复项是一样的。

注意题目中的提醒：

原地移除
不要使用额外空间
元素顺序可以改变
不需要考虑数组中超出新长度后面的元素

class Solution {
    public int removeElement(int[] nums, int val) {
        int i = 0, j = 0;
        while (j < nums.length) {
            if (nums[j] == val) {
                j++;
            } else {
                nums[i] = nums[j];
                i++;
                j++;
            }
        }
        return i;
    }
}

用的也是双指针的方式

官方思路

在这里插入图片描述

参考

移除元素

28. 实现 strStr()

实现 strStr() 函数。

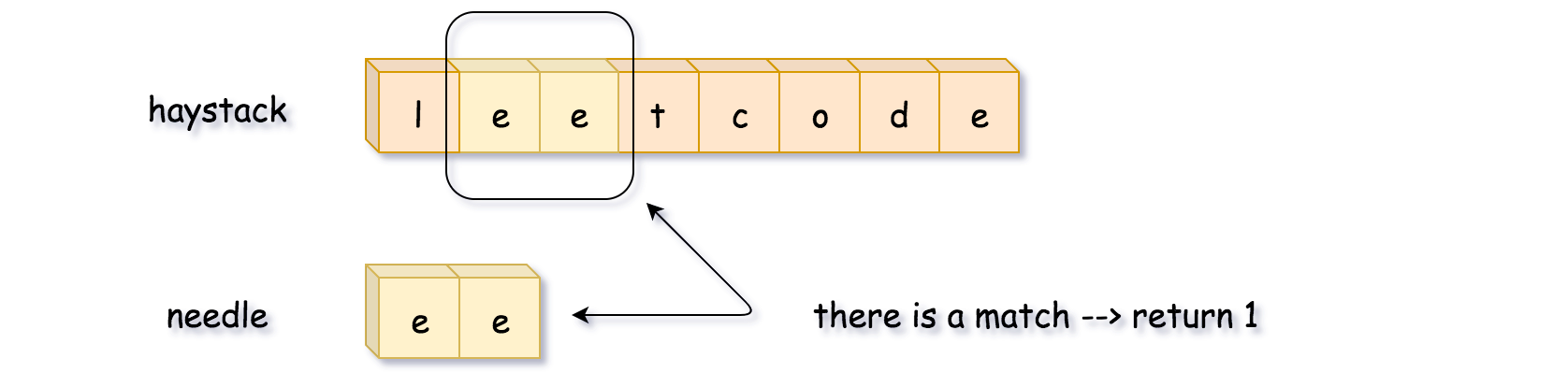
给定一个 haystack 字符串和一个 needle 字符串，在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在，则返回 -1。

示例 1:

输入: haystack = “hello”, needle = “ll”
输出: 2

示例 2:

输入: haystack = “aaaaa”, needle = “bba”
输出: -1

说明:

当 needle 是空字符串时，我们应当返回什么值呢？这是一个在面试中很好的问题。

对于本题而言，当 needle 是空字符串时我们应当返回 0 。这与C语言的 strstr() 以及 Java的 indexOf() 定义相符。

个人思路

如果needle为空，则返回 0
如果haystack 和 needle 长度相等，且字符串相等，则返回0
如果haystack的长度小于needle，则返回-2
如果haystack 和 needle 长度相等，但是字符串不相等，则返回-2
For循环，不断从haystack中截取与needle长度一致的字符串进行比较。得到我们想要的结果

class Solution {
    public int strStr(String haystack, String needle) {
        if (needle.length() == 0 || (haystack.length() == needle.length() && needle.equals(haystack))) {
            return 0;
        }
        if (haystack.length() < needle.length() || (haystack.length() == needle.length() && !needle.equals(haystack))) {
            return -1;
        }
        for (int i = 0, j = needle.length(); j <= haystack.length(); i++, j++) {
            if (haystack.substring(i, j).equals(needle)) {
                return i;
            }
        }
        return -1;
    }
}

结果：成功

官方代码 - 子串逐一比较 - 线性时间复杂度

fig

class Solution {
  public int strStr(String haystack, String needle) {
    int L = needle.length(), n = haystack.length();

    for (int start = 0; start < n - L + 1; ++start) {
      if (haystack.substring(start, start + L).equals(needle)) {
        return start;
      }
    }
    return -1;
  }
}

★官方代码 - 双指针 - 线性时间复杂度

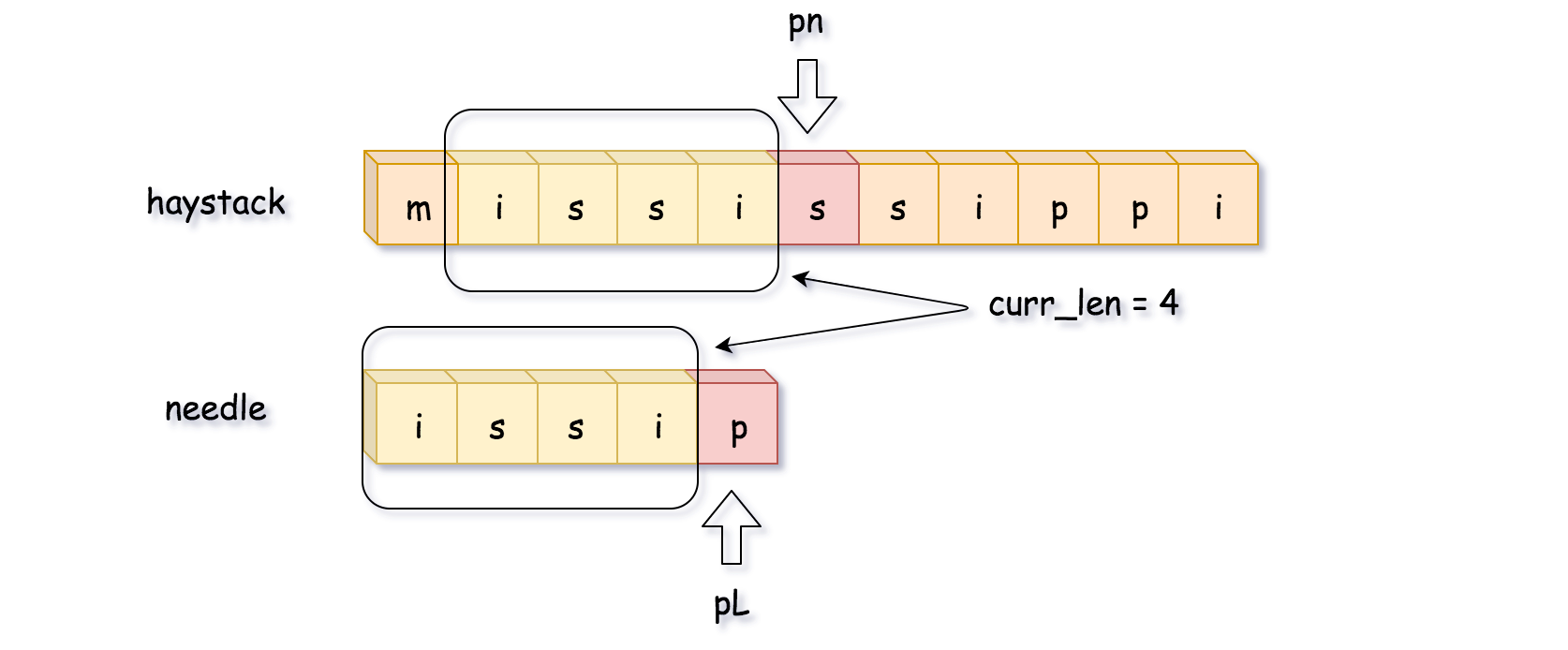
上一个方法的缺陷是会将 haystack 所有长度为 L 的子串都与 needle 字符串比较，实际上是不需要这么做的。

首先，只有子串的第一个字符跟 needle 字符串第一个字符相同的时候才需要比较。

fig

其次，可以一个字符一个字符比较，一旦不匹配了就立刻终止。

fig

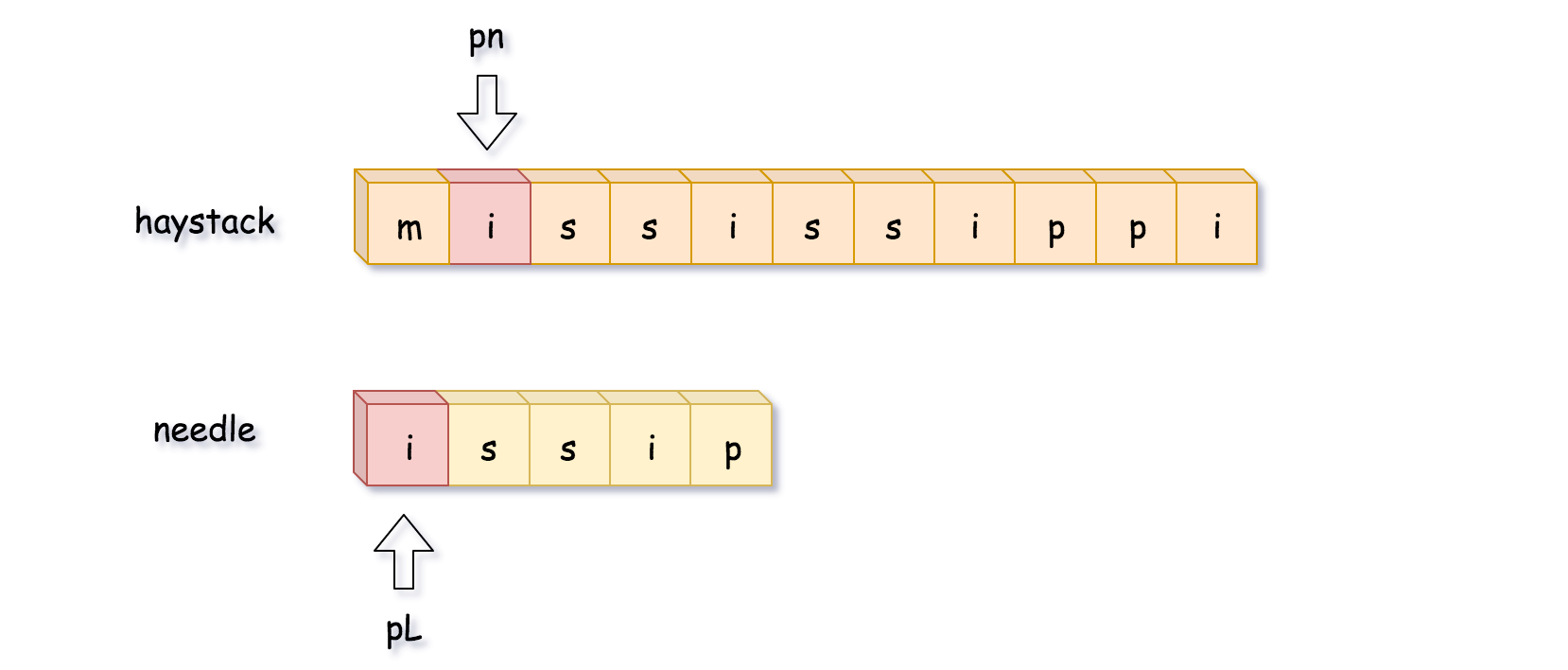
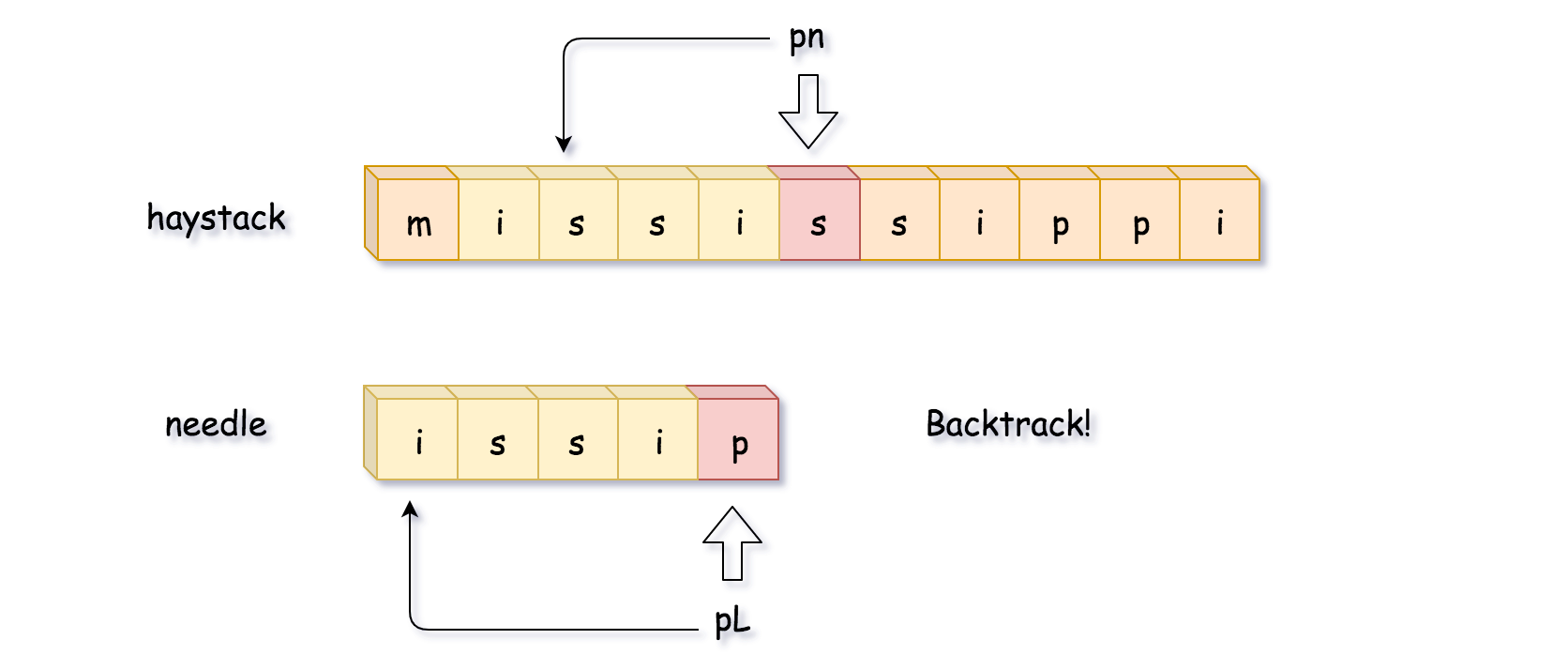
如下图所示，比较到最后一位时发现不匹配，这时候开始回溯。需要注意的是，pn 指针是移动到 pn = pn - curr_len + 1 的位置，而不是 pn = pn - curr_len 的位置。

fig

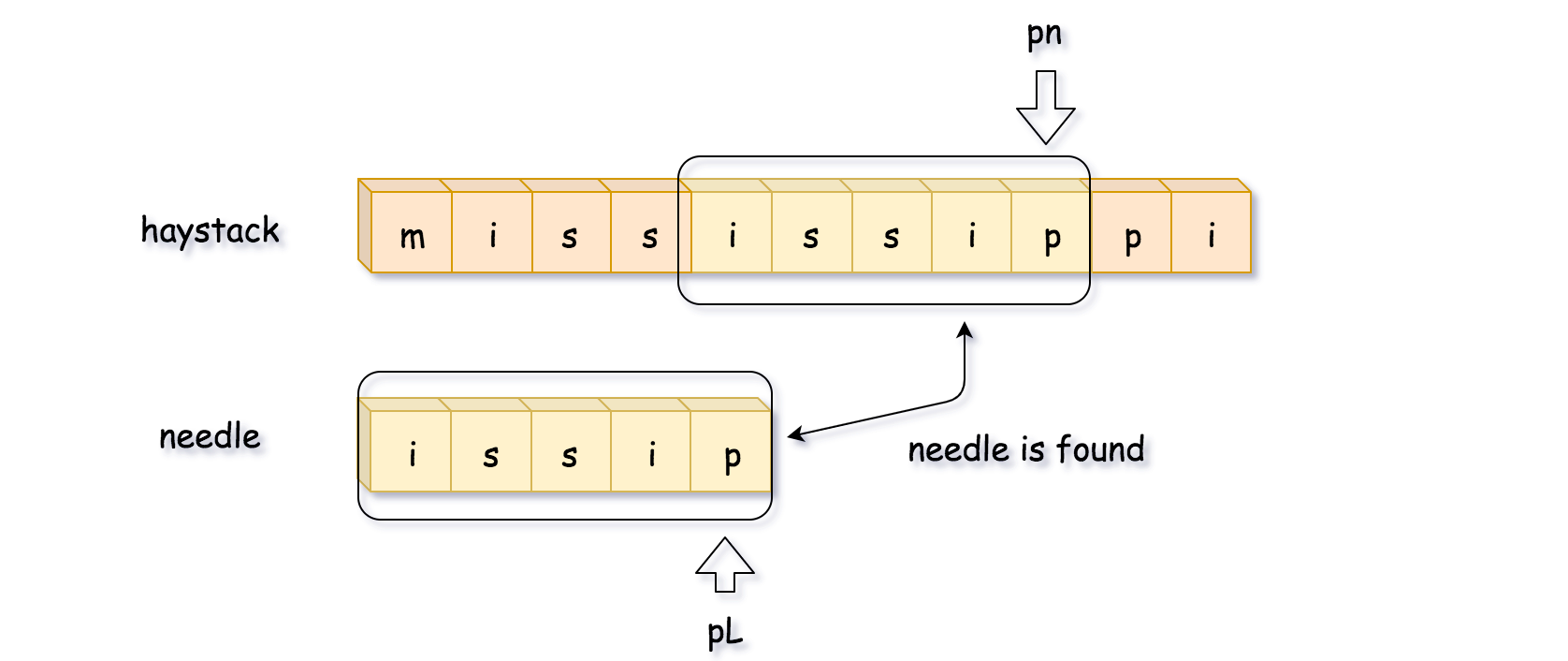
这时候再比较一次，就找到了完整匹配的子串，直接返回子串的开始位置 pn - L。

fig

class Solution {
  public int strStr(String haystack, String needle) {
    int L = needle.length(), n = haystack.length();
    if (L == 0) return 0;

    int pn = 0;
    while (pn < n - L + 1) {
      // find the position of the first needle character
      // in the haystack string
      while (pn < n - L + 1 && haystack.charAt(pn) != needle.charAt(0)) ++pn;

      // compute the max match string
      int currLen = 0, pL = 0;
      while (pL < L && pn < n && haystack.charAt(pn) == needle.charAt(pL)) {
        ++pn;
        ++pL;
        ++currLen;
      }

      // if the whole needle string is found,
      // return its start position
      if (currLen == L) return pn - L;

      // otherwise, backtrack
      pn = pn - currLen + 1;
    }
    return -1;
  }
}

参考

实现 strStr()

35. 搜索插入位置

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

你可以假设数组中无重复元素。

示例 1:

输入: [1,3,5,6], 5
输出: 2

示例 2:

输入: [1,3,5,6], 2
输出: 1

示例 3:

输入: [1,3,5,6], 7
输出: 4

示例 4:

输入: [1,3,5,6], 0
输出: 0

个人思路1

整个数组遍历一次，遇到小于等于某个值时，返回该值下标。

class Solution {
    public int searchInsert(int[] nums, int target) {
        for (int i = 0; i < nums.length; i++) {
            if (target <= nums[i]) {
                return i;
            }
        }
        return nums.length;
    }
}

个人思路2：二分查找

class Solution {
    public int searchInsert(int[] nums, int target) {
        int min = 0;
        int max = nums.length;
        while (min < max) {
            int middle = (max + min) / 2;
            if (nums[middle] >= target) {
                max = middle;
            } else {
                min = middle + 1;
            }
        }
        return min;
    }
}

69. x 的平方根

实现 int sqrt(int x) 函数。
计算并返回 x 的平方根，其中 x 是非负整数。
由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

示例 1:
输入: 4
输出: 2

示例 2:
输入: 8
输出: 2
说明: 8 的平方根是 2.82842…,
由于返回类型是整数，小数部分将被舍去。

代码

class Solution {
    public int mySqrt(int x) {
        int min = 0;
        int max = x;
        if (x == 1) {
            return 1;
        }
        while (max - min > 1) {
            int mid = (max - min) / 2 + min;
            if (x / mid >= mid) {
                min = mid;
            } else {
                max = mid;
            }
        }
        return min;
    }
}

167. 两数之和 II - 输入有序数组

给定一个已按照升序排列 的有序数组，找到两个数使得它们相加之和等于目标数。
函数应该返回这两个下标值 index1 和 index2，其中 index1 必须小于 index2。

说明:
返回的下标值（index1 和 index2）不是从零开始的。
你可以假设每个输入只对应唯一的答案，而且你不可以重复使用相同的元素。

示例:
输入: numbers = [2, 7, 11, 15], target = 9
输出: [1,2]
解释: 2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。

代码

class Solution {
    public int[] twoSum(int[] numbers, int target) {
        for (int i = 0; i < numbers.length; i++) {
            int min = i + 1;
            int max = numbers.length - 1;
            while (min <= max) {
                int middle = (max - min) / 2 + min;
                if (numbers[i] + numbers[middle] == target) {
                    return new int[]{i + 1, middle + 1};
                } else if (numbers[i] + numbers[middle] > target) {
                    max = middle - 1;
                } else {
                    min = middle + 1;
                }
            }
        }
        return null;
    }
}

第一个错误的版本

你是产品经理，目前正在带领一个团队开发新的产品。不幸的是，你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的，所以错误的版本之后的所有版本都是错的。

假设你有 n 个版本 [1, 2, ..., n]，你想找出导致之后所有版本出错的第一个错误的版本。

你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。

示例:

给定 n = 5，并且 version = 4 是第一个错误的版本。

调用 isBadVersion(3) -> false
调用 isBadVersion(5) -> true
调用 isBadVersion(4) -> true

所以，4 是第一个错误的版本。

代码

public class Solution extends VersionControl {
    public int firstBadVersion(int n) {
        int left = 1;
        int right = n;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (isBadVersion(mid)) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }
}

53. 最大子序和

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:

输入: [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

进阶:

如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的分治法求解。

个人思路

暴力破解，用Set记录下每一次计算的结果，最后返回最大值

class Solution {
    public int maxSubArray(int[] nums) {
        Set<Integer> resultSet = new HashSet<>();
        for (int i = 0; i < nums.length; i++) {
            int sum = 0;
            for (int j = i; j < nums.length; j++) {
                sum += nums[j];
                resultSet.add(sum);
            }
            resultSet.add(nums[i]);
        }
        return resultSet.stream().max((x, y) -> x > y ? 1 : -1).orElse(0);
    }
}

结果：失败，超出时间限制

官网思路

动态规划的是首先对数组进行遍历，当前最大连续子序列和为 sum，结果为 ans
如果 sum > 0，则说明 sum 对结果有增益效果，则 sum 保留并加上当前遍历数字
如果 sum <= 0，则说明 sum 对结果无增益效果，需要舍弃，则 sum 直接更新为当前遍历数字
每次比较 sum 和 ans的大小，将最大值置为ans，遍历结束返回结果
时间复杂度：O(n)

class Solution {
    public int maxSubArray(int[] nums) {
        int ans = nums[0];
        int sum = 0;
        for(int num: nums) {
            if(sum > 0) {
                sum += num;
            } else {
                sum = num;
            }
            ans = Math.max(ans, sum);
        }
        return ans;
    }
}

参考

画解算法：53. 最大子序和

66. 加一

给定一个由整数组成的非空数组所表示的非负整数，在该数的基础上加一。

最高位数字存放在数组的首位，数组中每个元素只存储单个数字。

你可以假设除了整数 0 之外，这个整数不会以零开头。

示例 1：

输入：digits = [1,2,3]
输出：[1,2,4]
解释：输入数组表示数字 123。

示例 2：

输入：digits = [4,3,2,1]
输出：[4,3,2,2]
解释：输入数组表示数字 4321。

示例 3：

输入：digits = [0]
输出：[1]

提示：

1 <= digits.length <= 100
0 <= digits[i] <= 9

个人思路1

将数组转成字符串
将String转换成Long
再将Long转换成数组

class Solution {
    public int[] plusOne(int[] digits) {
        StringBuilder stringBuilder = new StringBuilder();
        for (int digit : digits) {
            stringBuilder.append(digit);
        }
        Long digit = Long.valueOf(stringBuilder.toString());
        digit += 1;

        String stringResult = String.valueOf(digit);
        int length = stringResult.length();
        int[] result = new int[length];

        for (int i = 0; i < length; i++) {
            result[i] = Integer.valueOf(String.valueOf(stringResult.charAt(i)));
        }
        return result;
    }
}

结果：失败

在这里插入图片描述

个人思路2

从后往前取值
遇到值不等于9，则加一，返回。
遇到值等于9，则改此值

class Solution {
    public int[] plusOne(int[] digits) {
        for (int i = digits.length - 1; i >= 0; i--) {
        	// 不等于9，加一返回
            if (digits[i] != 9) {
                digits[i] += 1;
                return digits;
            }
            // 等于9，修改为0
            digits[i] = 0;
        }
        // 给的数组中所有下标对应的值都为9，则初始化新的数组，首位为1，其余皆为0
        int[] result = new int[digits.length + 1];
        result[0] = 1;
        return result;
    }
}

参考

LeetCode - 加一

38. 外观数列

给定一个正整数 n ，输出外观数列的第 n 项。

「外观数列」是一个整数序列，从数字 1 开始，序列中的每一项都是对前一项的描述。

你可以将其视作是由递归公式定义的数字字符串序列：

countAndSay(1) = “1”
countAndSay(n) 是对 countAndSay(n-1) 的描述，然后转换成另一个数字字符串。

前五项如下：

1
11
21
1211
111221

第一项是数字 1
描述前一项，这个数是 1 即 “ 一个 1 ”，记作 “11”
描述前一项，这个数是 11 即 “ 二个 1 ” ，记作 “21”
描述前一项，这个数是 21 即 “ 一个 2 + 一个 1 ” ，记作 “1211”
描述前一项，这个数是 1211 即 “ 一个 1 + 一个 2 + 二个 1 ” ，记作 “111221”

要 描述 一个数字字符串，首先要将字符串分割为最小数量的组，每个组都由连续的最多相同字符组成。然后对于每个组，先描述字符的数量，然后描述字符，形成一个描述组。要将描述转换为数字字符串，先将每组中的字符数量用数字替换，再将所有描述组连接起来。

例如，数字字符串 "3322251" 的描述如下图：
在这里插入图片描述

示例 1：

输入：n = 1
输出：“1”
解释：这是一个基本样例。

示例 2：

输入：n = 4
输出：“1211”
解释：
countAndSay(1) = “1”
countAndSay(2) = 读 “1” = 一个 1 = “11”
countAndSay(3) = 读 “11” = 二个 1 = “21”
countAndSay(4) = 读 “21” = 一个 2 + 一个 1 = “12” + “11” = “1211”

提示：

1 <= n <= 30

个人思路：循环

主要是记住同样的数字出现的次数，如：21 之后的数：

数字2 出现了 1次，记为：12
数字1 出现了 1次，记为：11
将两者拼接起来为：1211

class Solution {
    public String countAndSay(int n) {
        String preResult = "1";
        if (n == 1) {
            return preResult;
        }

        StringBuilder result = new StringBuilder();

        for (int i = 2; i <= n; i++) {
            int count = 0;
            char target = preResult.charAt(0);
            result = new StringBuilder();
            for (int j = 0; j < preResult.length(); j++) {
                if (target != preResult.charAt(j)) {
                    result.append(count);
                    result.append(target);

                    target = preResult.charAt(j);
                    count = 1;
                } else {
                    count++;
                }
                if (j + 1 == preResult.length()) {
                    result.append(count);
                    result.append(target);
                }
            }
            preResult = result.toString();
        }
        return result.toString();
    }
}

上述代码优化一下

class Solution {
    public String countAndSay(int n) {
        String preResult = "1";
        if (n == 1) {
            return preResult;
        }

        for (int i = 2; i <= n; i++) {
            int count = 1;
            char target = preResult.charAt(0);
            StringBuilder result = new StringBuilder();
            for (int j = 1; j < preResult.length(); j++) {
                if (target == preResult.charAt(j)) {
                    count++;
                } else {
                    result.append(count);
                    result.append(target);

                    target = preResult.charAt(j);
                    count = 1;
                }
            }
            result.append(count);
            result.append(target);
            preResult = result.toString();
        }
        return preResult;
    }
}

其他思路：递归

比如 n=6时,那么用递归得到上一层的字符串str=“111221”
我们将start指向下标0,我们从下标1开始遍历,遍历到“2”下标3的时候,sb拼上(3-0)个1即sb.append(3).append(1),将start指针指向下标3,接着重复以上操作,直到到达str的最后一位,sb直接拼上即可。

class Solution {
    public String countAndSay(int n) {
        // 递归终止条件
        if (n == 1) {
            return "1";
        }
        StringBuffer res = new StringBuffer();
        // 拿到上一层的字符串
        String str = countAndSay(n - 1);
        int length = str.length();
        // 开始指针为0
        int start = 0;
        // 注意这从起始条件要和下面长度统一
        for (int i = 1; i < length + 1; i++) {
            // 字符串最后一位直接拼接
            if (i == length) {
                res.append(i - start).append(str.charAt(start));
            // 直到start位的字符串和i位的字符串不同，拼接并更新start位
            } else if (str.charAt(i) != str.charAt(start) ) {
                res.append(i - start).append(str.charAt(start));
                start = i;
            }
        }
        return res.toString();
    }
}

参考

ruo-guang - 外观数列

414. 第三大的数

给你一个非空数组，返回此数组中第三大的数。如果不存在，则返回数组中最大的数。
示例1：

输入：[3, 2, 1]
输出：1
解释：第三大的数是 1 。

示例2：

输入：[1, 2]
输出：2
解释：第三大的数不存在, 所以返回最大的数 2 。

示例3：

输入：[2, 2, 3, 1]
输出：1
解释：注意，要求返回第三大的数，是指在所有不同数字中排第三大的数。
此例中存在两个值为 2 的数，它们都排第二。在所有不同数字中排第三大的数为 1 。

题解一

使用TreeSet排序 + 去重，如果最后得到的集合大小 <= 2，则取最大值(treeSet.last())。否则，取第三大的值。

    public int thirdMax(int[] nums) {
        TreeSet<Integer> treeSet = new TreeSet<>();

        for (int num : nums) {
            treeSet.add(num);
        }

        if (treeSet.size() <= 2) {
            return treeSet.last();
        }

        treeSet.pollLast();
        treeSet.pollLast();
        return treeSet.last();
    }

题解二

还是使用TreeSet排序 + 去重，不过保持集合的大小不超过3，如果超过3，则remove最小值。
根据最后得到的集合大小判断，如果最后得到的集合大小 <= 2，则取集合的最大值(treeSet.last())。否则，取集合的最小值(treeSet.first())。

    public int thirdMax(int[] nums) {
        TreeSet<Integer> treeSet = new TreeSet<>();

        for (int num : nums) {
            treeSet.add(num);
            if (treeSet.size() > 3) {
                // 拿到最小的值，删除
                treeSet.remove(treeSet.pollFirst());
            }
        }

        return treeSet.size() >= 3 ? treeSet.first() : treeSet.last();
    }

题解三

不需要排序 + 一次遍历

    public int thirdMax3(int[] nums) {
        Integer a = null;
        Integer b = null;
        Integer c = null;

        for (int num : nums) {
            if (a == null || num > a) {
                c = b;
                b = a;
                a = num;
                continue;
            }

            if ((b == null || num > b) && a > num) {
                c = b;
                b = num;
                continue;
            }

            if ((c == null || num > c) && (b != null && b > num)) {
                c = num;
            }
        }
        return c == null ? a : c;
    }

11. 盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。

说明：你不能倾斜容器。
示例 1：

输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

提示：

n == height.length
2 <= n <= 105
0 <= height[i] <= 104

题解一：双循环（暴力破解）

// 暴力破解，双循环，超出时间限制
public int maxArea(int[] height) {
    int maxArea = 0;
    for (int i = 0; i < height.length - 1; i++) {
        for (int j = i + 1; j < height.length; j++) {
            // 求出当前两个距离的面积
            int currentArea = Math.min(height[i], height[j]) * (j - i);
            // 取得最大面积
            maxArea = Math.max(maxArea, currentArea);
        }
    }
    return maxArea;
}

题解二：双指针

// 双指针
public int maxArea(int[] height) {
    int maxArea = 0;
    int left = 0;
    int right = height.length - 1;
    while (left < right) {
        // 求出当前两个距离的面积
        int currentArea = Math.min(height[left], height[right]) * (right - left);
        // 取得最大面积
        maxArea = Math.max(maxArea, currentArea);
        if (height[left] < height[right]) {
            left++;
        } else {
            right++;
        }
    }
    return maxArea;
}

746. 使用最小花费爬楼梯

给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。

请你计算并返回达到楼梯顶部的最低花费。

示例 1：

输入：cost = [10,15,20]
输出：15
解释：你将从下标为 1 的台阶开始。
支付 15 ，向上爬两个台阶，到达楼梯顶部。总花费为 15 。

示例 2：

输入：cost = [1,100,1,1,1,100,1,1,100,1]
输出：6
解释：你将从下标为 0 的台阶开始。

支付 1 ，向上爬两个台阶，到达下标为 2 的台阶。
支付 1 ，向上爬两个台阶，到达下标为 4 的台阶。
支付 1 ，向上爬两个台阶，到达下标为 6 的台阶。
支付 1 ，向上爬一个台阶，到达下标为 7 的台阶。
支付 1 ，向上爬两个台阶，到达下标为 9 的台阶。
支付 1 ，向上爬一个台阶，到达楼梯顶部。总花费为 6 。

提示：

2 <= cost.length <= 1000
0 <= cost[i] <= 999

题解一

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int n = cost.length;
        int[] dp = new int[n + 1];
        dp[0] = dp[1] = 0;
        for (int i = 2; i <= n; i++) {
            dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
        }
        return dp[n];
    }
}

题解二

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int n = cost.length;
        int pre = 0;
        int curr = 0;
        for (int i = 2; i <= n; i++) {
            int next = Math.min(curr + cost[i - 1], pre + cost[i - 2]);
            pre = curr;
            curr = next;
        }
        return curr;
    }
}

338. 比特位计数

给你一个整数 n ，对于 0 <= i <= n 中的每个 i ，计算其二进制表示中 1 的个数，返回一个长度为 n + 1 的数组 ans 作为答案。

示例 1：

输入：n = 2
输出：[0,1,1]
解释：

0 --> 0
1 --> 1
2 --> 10

示例 2：

输入：n = 5
输出：[0,1,1,2,1,2]
解释：

0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101

提示：

0 <= n <= 105

题解一

class Solution {
    /**
     * 方式一：暴力破解
     * 1. 遍历 0 - n
     * 2. 每个值都计算出它的二进制中包含1的个数
     * 问题：目标值太大时，有很多数字计算二进制的过程是重复的
     *
     * @param n 目标值
     * @return 目标值范围中，二进制中包含1的个数
     */
    public int[] countBits(int n) {
        // 初始化必要值
        int[] results = new int[n + 1];

        // 遍历 0 - n
        for (int i = 0; i <= n; i++) {
            // 依次获得每个值的二进制中1的个数
            int result = getOneNumber(i);

            // 保存结果
            results[i] = result;
        }

        // 返回结果
        return results;
    }

    private int getOneNumber(int number) {
        int count = 0;
        int n = number;
        while (n != 0) {
            if (n % 2 == 1) {
                count++;
            }
            n /= 2;
        }
        return count;
    }
}

题解二

class Solution {
    private static HashMap<Integer, Integer> records = new HashMap<>();

    /**
     * 方式二：在方式一的基础上，加上“缓存”，记录之前得到的数字和二进制中包含1的个数之间的关系
     *
     * @param n
     * @return
     */
    public int[] countBits(int n) {
        // 初始化必要值
        int[] results = new int[n + 1];

        // 遍历 0 - n
        for (int i = 0; i <= n; i++) {
            // 依次获得每个值的二进制中1的个数
            int result = getOneNumber2(i);

            // 保存结果
            results[i] = result;
        }

        // 返回结果
        return results;
    }

    private int getOneNumber2(int number) {
        int count = 0;
        int n = number;
        while (n != 0) {
            if (records.containsKey(n)) {
                count += records.get(n);
                records.put(number, count);
                return count;
            }

            if (n % 2 == 1) {
                count++;
            }
            n /= 2;
        }
        records.put(number, count);
        return count;
    }
}

题解三

class Solution {
    /**
     * 官方解法一：Brian Kernighan 算法
     * 算法解释：对于任意整数 x，令 x = x & (x - 1)，该运算将 x 的二进制表示的最后一个 1 变成 0。因此，对 x 重复该操作，直到 x 变成 0，则操作次数即为 x 的「一比特数」
     *
     * @param n
     * @return
     */
    public int[] countBits(int n) {
        int[] bits = new int[n + 1];
        for (int i = 0; i <= n; i++) {
            bits[i] = countOnes(i);
        }
        return bits;
    }

    private int countOnes(int x) {
        int ones = 0;
        while (x > 0) {
            x &= (x - 1);
            ones++;
        }
        return ones;
    }
}

1025. 除数博弈

爱丽丝和鲍勃一起玩游戏，他们轮流行动。爱丽丝先手开局。
最初，黑板上有一个数字 n 。在每个玩家的回合，玩家需要执行以下操作：

选出任一 x，满足 0 < x < n 且 n % x == 0 。
用 n - x 替换黑板上的数字 n 。

如果玩家无法执行这些操作，就会输掉游戏。
只有在爱丽丝在游戏中取得胜利时才返回 true 。假设两个玩家都以最佳状态参与游戏。

示例 1：

输入：n = 2
输出：true
解释：爱丽丝选择 1，鲍勃无法进行操作。

示例 2：

输入：n = 3
输出：false
解释：爱丽丝选择 1，鲍勃也选择 1，然后爱丽丝无法进行操作。

提示：

1 <= n <= 1000

解题一

class Solution {
    public boolean divisorGame(int n) {
        return n % 2 == 0;
    }
}

解题二

class Solution {
    public boolean divisorGame(int n) {
        boolean[] result = new boolean[n + 1];

        result[0] = false;
        result[1] = true;
        for (int i = 3; i <= n; i++) {
            for (int j = 1; j < i; j++) {
                if ((i % j == 0) && !result[i - j - 1]) {
                    result[i - 1] = true;
                    break;
                }
            }
        }
        return result[n - 1];
    }
}