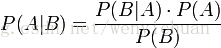数学原理： 贝叶斯定理

贝叶斯定理由英国数学家贝叶斯 ( Thomas Bayes 1702-1761 ) 发展，用来描述两个条件概率之间的关系。 
所谓”拼写检查”，就是在发生输入错误B的情况下，试图推断出A。从概率论的角度看，就是已知输入错误B，然后在若干个备选方案中，找出可能性最大的那个输入正确A，也就是求下面这个式子的最大值。 
（比如lates应该被更正为late或者latest？），我们用概率决定把哪一个作为建议。我们从跟原始词相关的所有可能的正确拼写中找到可能性最大的那个拼写建议。 

事件A：要猜测输入正确事件的概率 
事件B：现实已发生输入错误事件的概率

对于每一个A来说，输入错误B的概率相同，所以最大值可转换为

P(B|A)*P(A)

其中

P（A|B）是在拼写错误的情况下推断出拼写正确的情况

P(A)的含义是某个正确的词的出现”概率”，它可以用”频率”代替。如果我们有一个足够大的文本库，那么这个文本库中每个单词的出现频率，就相当于它的发生概率。某个词的出现频率越高，P(A）就越大。

P(B|A)的含义是，在试图拼写正确A的情况下，出现拼写错误B的概率。这需要统计数据的支持，但是为了简化问题，我们假设两个单词在组成上越接近，就有越可能拼错，P(B|A)就越大。举例来说，相差一个字母的拼法，就比相差两个字母的拼法，发生概率更高。你想拼写单词hello，那么错误拼成hallo（相差一个字母）的可能性，就比拼成haallo高（相差两个字母）。

因此

我们只要找到与输入单词在组成上最相近的那些词，再在其中挑出出现频率最高的一个，就能实现 P(B|A) * P(A) 的最大值。

正因贝叶斯公式可用于事件发生概率的推测，因此它广泛应用于计算机领域如：垃圾邮件的过滤，中文分词，机器翻译，拼写检查等等。

实例：拼写检查器

算法实现

1. 建立一个足够大的文本库。读取一个包含了一百万个单词的很大的文本文件big.txt。这个文件由Project Gutenberg中几个公共领域的书串联而成。
2. 取出文本库的每一个单词，统计它们的出现频率。
3. 根据用户输入的单词，得到其所有可能的拼写相近的形式。 
   所谓”拼写相近”，指的是两个单词之间的”编辑距离”（edit distance）不超过2。也就是说，两个词只相差1到2个字母，只通过