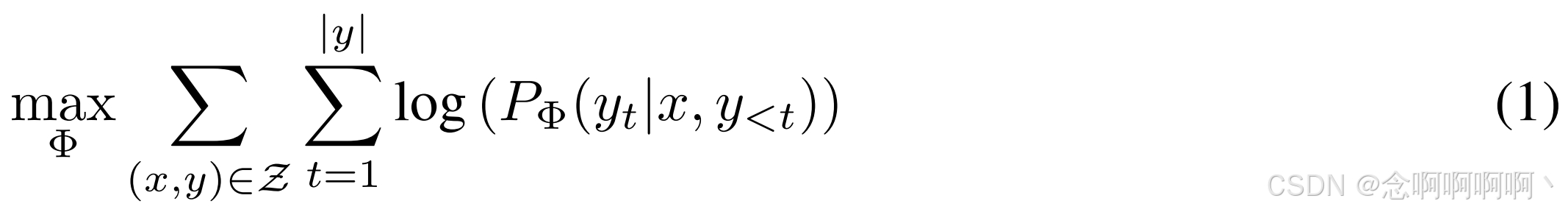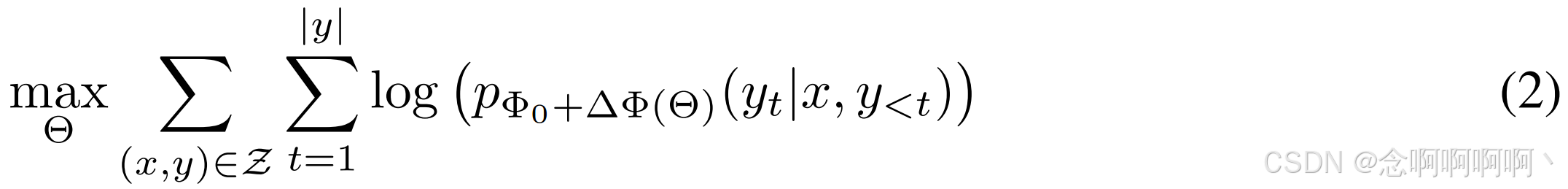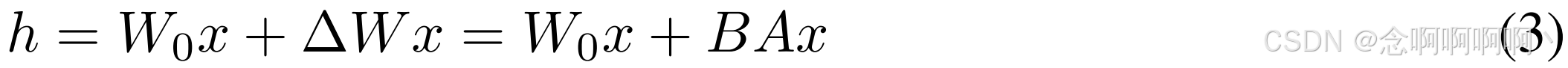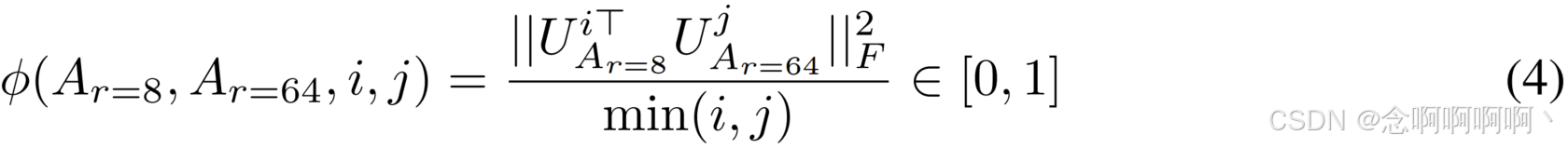LoRA：大型语言模型的低秩自适应

作者：Edward Hu, Yelong Shen, Phillip Wallis, Zeyuan Allen-Zhu, Yuanzhi Li, Shean Wang, Lu Wang, Weizhu Chen
单位：Microsoft Corporation
论文地址：2021-arXiv-LoRA: Low-Rank Adaptation of Large Language Models

摘要

 自然语言处理的一个重要范例是对通用领域数据进行大规模预训练，并适应特定任务或领域。随着我们对更大的模型进行预训练，完全微调（重新训练所有模型参数）变得不太可行。以 GPT-3 175B 为例 - 部署经过微调的模型的独立实例（每个实例有 175B 个参数）的成本过高。我们提出了低秩自适应（Low-Rank Adaptation，LoRA），它冻结了预训练的模型权重，并将可训练的秩分解矩阵注入 Transformer 架构的每一层，大大减少了下游任务的可训练参数数量。与使用 Adam 微调的 GPT-3 175B 相比，LoRA 可以将可训练参数的数量减少 10,000 倍，并将 GPU 内存需求减少 3 倍。尽管 LoRA 的可训练参数更少、训练吞吐量更高，并且与适配器不同，没有额外的推理延迟，但其在 RoBERTa、DeBERTa、GPT-2 和 GPT-3 上的模型质量表现与微调相当或更好。我们还对语言模型自适应中的秩缺陷进行了实证研究，这揭示了 LoRA 的有效性。我们发布了一个软件包，以促进 LoRA 与 PyTorch 模型的集成，并在 https://github.com/microsoft/LoRA 上提供了我们对 RoBERTa、DeBERTa 和 GPT-2 的实现和模型检查点。

1. 引言

 自然语言处理中的许多应用都依赖于将一个大规模、预训练的语言模型适配到多个下游应用。这种适配通常通过微调来完成，微调会更新预训练模型的所有参数。微调的主要缺点是新模型包含的参数与原始模型一样多。随着更大的模型每隔几个月进行训练，这从 GPT-2 (Radford et al, b) 或 RoBERTa large (Liu et al, 2019) 的 “不便（inconvenience）” 变成了 GPT-3 (Brown et al, 2020) 的关键部署挑战，该模型具有 1750 亿个可训练参数。¹

⁰ 与 V1 版本相比，该草案包括更好的基线，GLUE 实验，以及更多关于适配器延迟的内容。
¹ GPT-3 175B 通过少次学习获得了非凡的性能，而微调可以显著提升其性能，如附录 A 所示。

 许多人试图通过仅调整一些参数或为新任务学习外部模块来缓解这种情况。这样，除了每个任务的预训练模型之外，我们只需要存储和加载少量特定于任务的参数，从而大大提高部署时的运行效率。然而，现有技术通常会通过扩展模型深度引入推理延迟 (Houlsby et al, 2019; Rebuffi et al, 2017) 或减少模型的可用序列长度 (Li & Liang, 2021; Lester et al, 2021; Hambardzumyan et al, 2020; Liu et al, 2021)（第 3 节）。更重要的是，这些方法通常无法匹配微调基线，从而在效率和模型质量之间造成权衡。

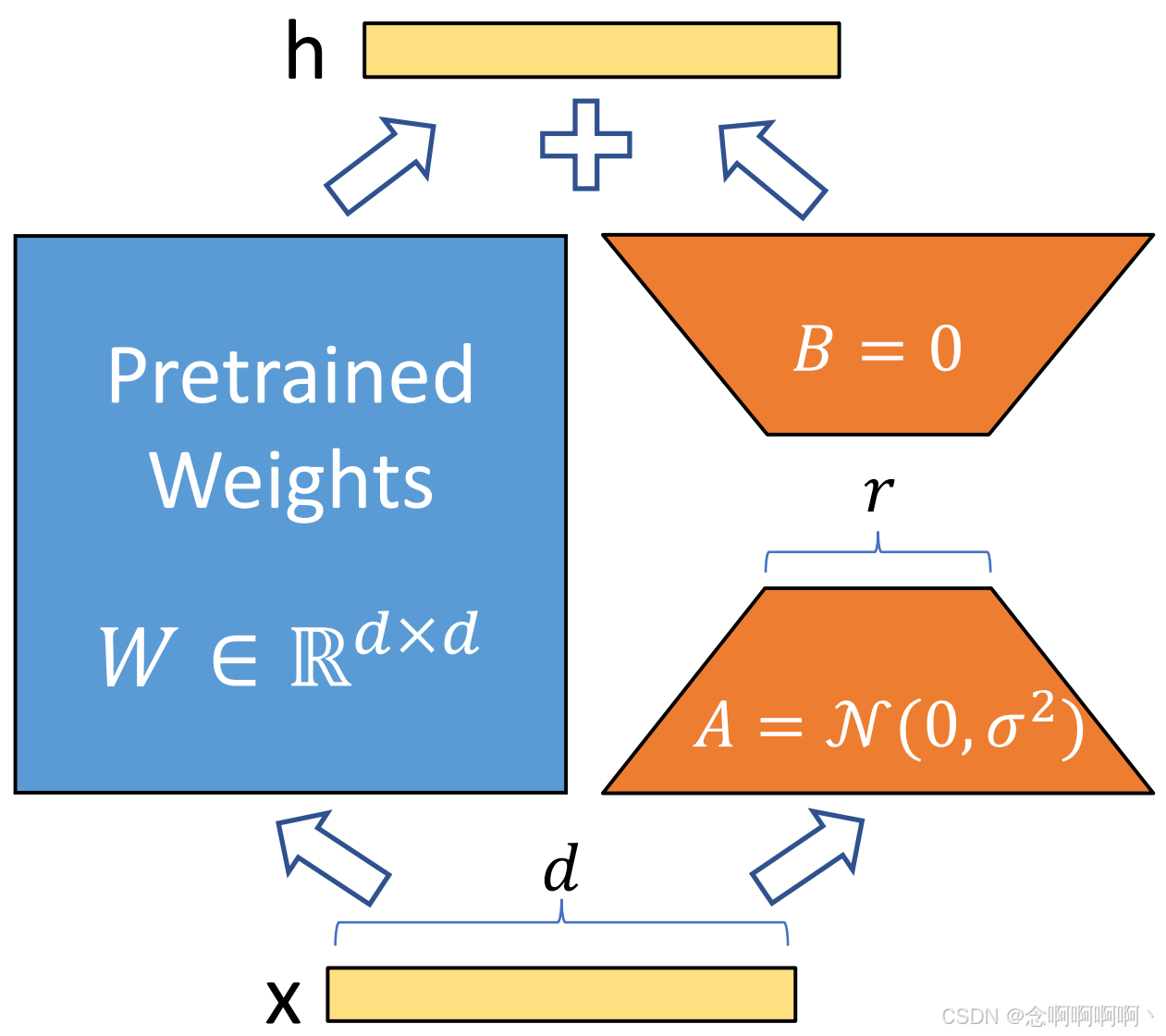
 我们从 Li et al. (2018a) 和 Aghajanyan et al. (2020) 的论文中汲取灵感，他们指出，学习到的过度参数化模型实际上存在于较低的内在维度上。我们假设模型适应过程中权重的变化也具有较低的 “内在秩（intrinsic rank）”，这导致了我们提出的低秩适应（Low-Rank Adaptation，LoRA）方法。LoRA 允许我们通过优化适应过程中密集层变化的秩分解矩阵来间接训练神经网络中的一些密集层，同时保持预训练权重不变，如图 1 所示。以 GPT-3 175B 为例，我们表明，即使满秩（即 $d$）高达 12,288，非常低的秩（即图 1 中的 $r$ 可以是一或二）也足够了，这使得 LoRA 既具有存储效率，又具有计算效率。

 LoRA 具有几个关键优势。

• 预先训练好的模型可以共享，并用于为不同的任务构建许多小型 LoRA 模块。我们可以通过替换图 1 中的矩阵 $A$ 和 $B$ 来冻结共享模型并高效切换任务，从而显著降低存储需求和任务切换开销。
• LoRA 使训练更加高效，并且在使用自适应优化器时将硬件进入门槛降低多达 3 倍，因为我们不需要计算梯度或维护大多数参数的优化器状态。相反，我们只优化注入的、小得多的低秩矩阵。
• 我们的简单线性设计允许我们在部署时将可训练矩阵与冻结权重合并，与完全微调的模型相比，通过构造不会引入推理延迟。
• LoRA 与许多先前的方法正交，可以与其中许多方法结合使用，例如前缀调整。我们在附录 E 中提供了一个示例。

 术语和惯例。我们经常提到 Transformer 架构，并使用常规术语表示其维度。我们将 Transformer 层的输入和输出维度大小称为 $d_{model}$。我们使用 $W_q$、$W_k$、$W_v$ 和 $W_o$ 来指代自注意力模块中的查询/键/值/输出投影矩阵。$W$ 或 $W_0$ 表示预训练的权重矩阵，$∆W$ 表示其在自适应过程中的累积梯度更新。我们使用 $r$ 表示 LoRA 模块的秩。我们遵循 (Vaswani et al, 2017; Brown et al, 2020) 规定的惯例，并使用 Adam (Loshchilov & Hutter, 2019; Kingma & Ba, 2017) 进行模型优化，并使用 Transformer MLP 前馈维度 $d_{ffn}=4\times d_{model}$。

2. 问题陈述

 虽然我们的提案与训练目标无关，但我们专注于语言建模作为我们的激励用例（motivating use case）。下面简要描述了语言建模问题，特别是在给定特定任务提示（task-specific prompt）的情况下最大化条件概率。

 假设我们得到了一个由 $\Phi$ 参数化的预训练自回归语言模型 $P_{\Phi }\left(y|x\right)$。例如，$P_{\Phi }\left(y|x\right)$ 可以是一个通用的多任务学习器，例如基于 Transformer 架构 (Vaswani et al, 2017) 的 GPT (Radford et al, b; Brown et al, 2020)。考虑将这个预训练模型应用于下游条件文本生成任务，例如摘要、机器阅读理解（MRC）和自然语言到 SQL（NL2SQL）。每个下游任务都由一个上下文-目标对的训练数据集表示： Z = { ( x i ,   y i ) } i = 1 ,   ⋯   ,   N \mathcal{Z}=\left\{\left(x_i,\ y_i\right)\right\}_{i=1,\ \cdots,\ N} Z={(xi​, yi​)}i=1, ⋯, N​，其中 $x_i$ 和 $y_i$ 都是标记序列。例如，在 NL2SQL 中，$x_i$ 是自然语言查询，$y_i$ 是其对应的 SQL 命令；对于摘要，$x_i$ 是文章的内容，$y_i$ 是其摘要。在完全微调期间，模型初始化为预训练权重 ${\Phi }_0$，并通过反复遵循梯度更新为 ${\Phi }_0+∆\Phi$，以最大化条件语言建模目标：

 完全微调的主要缺点之一是，对于每个下游任务，我们都会学习一组不同的参数 $∆\Phi$，其维度 $|∆\Phi |$ 等于 $|{\Phi }_0|$。因此，如果预训练模型很大（例如GPT-3，$|{\Phi }_0|\approx 1750$ 亿），存储和部署许多独立的微调模型实例可能会很困难，即使可行。

 在本文中，我们采用了一种参数效率更高的方法，其中任务特定的参数增量 $∆\Phi =∆\Phi \left(\Theta \right)$ 进一步由一组小得多的参数 $\Theta$ 进行编码，其中 $|\Theta |\ll |{\Phi }_0|$。因此，寻找 $∆\Phi$ 的任务变成了对 $\Theta$ 进行优化：

 在后续章节中，我们建议使用低秩表示来编码 $∆\Phi$，这样既节省计算资源又节省内存。当预训练模型为 GPT-3 175B 时，可训练参数 $|\Theta |$ 的数量可以小到 $|{\Phi }_0|$ 的 $0.01\%$。

3. 现有的解决方案还不够好吗？

 我们着手解决的问题绝不是新问题。自迁移学习诞生以来，已有数十项研究试图使模型自适应更加高效地提高参数和计算效率。有关一些著名作品的概述，请参阅第 6 节。以语言建模为例，在有效适应方面有两种突出的策略：添加适配器层 (Houlsby et al, 2019; Rebuffi et al, 2017; Pfeiffer et al, 2021; Ruckl ¨ e et al, 2020) 或优化输入层激活的某些形式 (Li & Liang, 2021; Lester et al, 2021; Hambardzumyan et al, 2020; Liu et al, 2021)。但是，这两种策略都有其局限性，尤其是在大规模和延迟敏感的生产场景中。

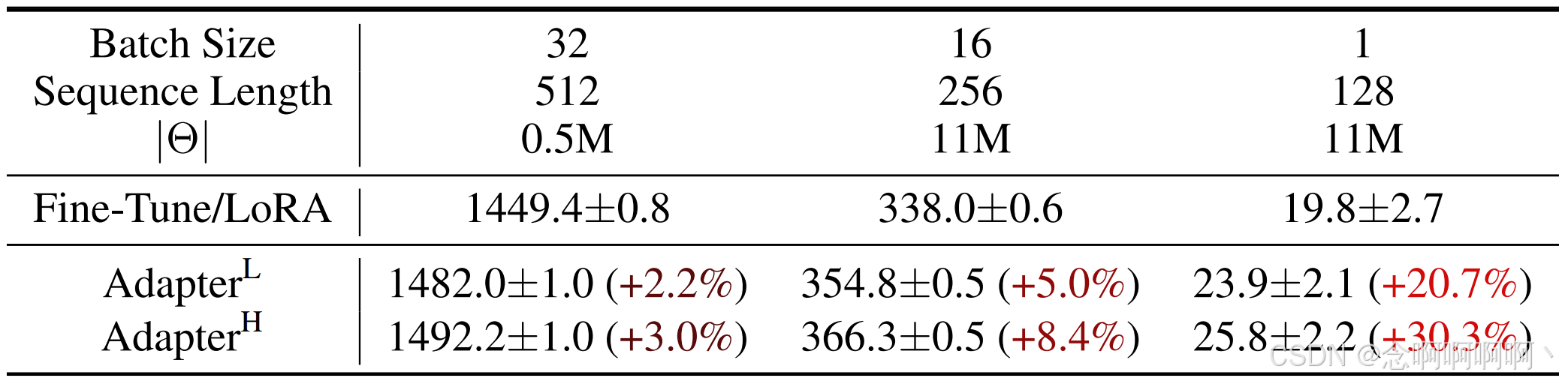
 适配器层引入了推理延迟（Inference Latency）。适配器（Adapter）有很多变体。我们重点关注 Houlsby et al (2019) 的原始设计，该设计每个 Transformer 块有两个适配器层，以及 Lin et al. (2020) 的最新设计，该设计每个块只有一个适配器层，但有一个额外的 LayerNorm (Ba et al., 2016)。虽然可以通过修剪层或利用多任务设置来减少总体延迟 (Ruckl ¨ e et al., 2020; Pfeiffer et al., 2021)，但没有直接的方法可以绕过适配器层中的额外计算。这似乎不是什么问题，因为适配器层被设计为具有很少的参数（有时 $<$ 原始模型的 $1\%$），具有较小的瓶颈维度，这限制了它们可以添加的 FLOP。然而，大型神经网络依靠硬件并行性来保持低延迟，并且适配器层必须按顺序处理。这在在线推理设置中产生了差异，因为批处理大小通常小到 1。在没有模型并行性的一般场景中，例如在单个 GPU 上运行 GPT-2 (Radford et al., b) 中等推理，我们发现使用适配器时延迟明显增加，即使瓶颈尺寸非常小（表 1）。

 当我们需要像 Shoeybi et al (2020); Lepikhin et al (2020) 所做的那样对模型进行分片时，这个问题会变得更加严重，因为额外的深度需要更多的同步 GPU 操作（例如 AllReduce 和 Broadcast），除非我们多次冗余地存储适配器参数。

 直接优化提示很难。另一个方向，以前缀调整 (Li & Liang, 2021) 为例，面临着不同的挑战。我们观察到前缀调整很难优化，并且其性能在可训练参数中非单调变化，证实了原始论文中的类似观察结果。更根本的是，保留一部分序列长度用于自适应必然会减少可用于处理下游任务的序列长度，我们怀疑这会使调整提示的性能低于其他方法。我们将任务性能的研究推迟到第 5 节。

4. 我们的方法

 我们描述了 LoRA 的简单设计及其实际优势。这里概述的原则适用于深度学习模型中的任何密集层，尽管我们在实验中仅关注 Transformer 语言模型中的某些权重作为激励用例。

4.1 低秩参数化更新矩阵

 神经网络包含许多执行矩阵乘法的密集层。这些层中的权重矩阵通常具有满秩。在适应特定任务时，Aghajanyan et al.
(2020) 表明，预训练的语言模型具有较低的 “固有维度（instrisic dimension）”，尽管随机投影到较小的子空间，但仍可以有效地学习。受此启发，我们假设权重的更新在适应过程中也具有较低的 “固有秩（intrinsic rank）”。对于预训练的权重矩阵 $W_0\in {\mathbb{R}}^{d\times k}$，我们通过使用低秩分解 $W_0+∆W=W_0+BA$ 来表示后者来限制其更新，其中 $B\in {\mathbb{R}}^{d\times r},A\in {\mathbb{R}}^{r\times k}$，秩为 $r\ll \min \left(d,k\right)$。在训练期间，$W_0$ 被冻结并且不接收梯度更新，而 $A$ 和 $B$ 包含可训练参数。注意，$W_0$ 和 $∆W=BA$ 都与相同的输入相乘，并且它们各自的输出向量按坐标相加。对于 $h=W_{0}x$，我们修改后的前向传递产生：

 我们在图 1 中说明了我们的重新参数化。我们对 $A$ 使用随机高斯初始化，对 $B$ 使用零，因此 $∆W=BA$ 在训练开始时为零。然后，我们将 $∆Wx$ 缩放 $\frac{\alpha }{r}$，其中 $\alpha$ 是 $r$ 中的常数。在使用 Adam 进行优化时，如果我们适当缩放初始化，则调整 $\alpha$ 与调整学习率大致相同。因此，我们只需将 $\alpha$ 设置为我们尝试的第一个 $r$，而不对其进行调整。这种缩放有助于减少在我们改变 $r$ 时重新调整超参数的需要 (Yang & Hu, 2021)。

 完全微调的概括（Full Fine-tuning）。更通用的微调形式允许训练预训练参数的子集。LoRA 更进一步，不需要在自适应期间对权重矩阵进行累积梯度更新以使其具有满秩。这意味着，当将 LoRA 应用于所有权重矩阵并训练所有偏差时²，我们通过将 LoRA 秩 $r$ 设置为预训练权重矩阵的秩来粗略地恢复完全微调的表现力。换句话说，随着可训练参数的数量的增加³，训练 LoRA 大致收敛到训练原始模型，而基于适配器的方法收敛到 MLP，基于前缀的方法收敛到不能接受长输入序列的模型。

 无额外推理延迟（Inference Latency）。在生产中部署时，我们可以明确计算并存储 $W=W_0+BA$ 并照常进行推理。请注意，$W_0$ 和 $BA$ 都在 ${\mathbb{R}}^{d\times k}$ 中。当我们需要切换到另一个下游任务时，我们可以通过减去 $BA$ 然后添加不同的 $B^{\prime }{A}^{\prime }$ 来恢复 $W_0$，这是一个快速的操作，内存开销非常小。至关重要的是，与通过构造微调的模型相比，这保证了我们不会在推理过程中引入任何额外的延迟。

² 与权重相比，它们代表的参数数量可以忽略不计。
³ 这是在适应艰巨任务时不可避免的。

4.2 将 LORA 应用于 Transformer

 原则上，我们可以将 LoRA 应用于神经网络中权重矩阵的任何子集，以减少可训练参数的数量。在 Transformer 架构中，自注意力模块中有四个权重矩阵（$W_q,W_k,W_v,W_o$），MLP 模块中有两个权重矩阵。我们将 $W_q$（或 $W_k,W_v$）视为维度为 $d^{model}\times d^{model}$ 的单个矩阵，即使输出维度通常被切分为注意力头。我们将研究限制为仅调整下游任务的注意力权重，并冻结 MLP 模块（因此它们不会在下游任务中接受训练），以简化和提高参数效率。我们将在第 7.1 节中进一步研究在 Transformer 中调整不同类型的注意力权重矩阵的影响。我们将调整 MLP 层、LayerNorm 层和偏差的实证研究留到未来的工作中。

 实际好处和局限性。最显著的好处来自内存和存储使用量的减少。对于使用 Adam 训练的大型 Transformer，如果 $r\ll d_{model}$，我们将 VRAM 使用量减少多达 2/3，因为我们不需要存储冻结参数的优化器状态。在 GPT-3 175B 上，我们将训练期间的 VRAM 消耗从 1.2TB 减少到 350GB。当 $r=4$ 且仅调整查询和值投影矩阵时，检查点大小减少了大约 10,000 倍（从 350GB 到 35MB）⁴。这使我们能够使用更少的 GPU 进行训练并避免 I/O 瓶颈。另一个好处是，我们可以在部署时以更低的成本在任务之间切换，只需交换 LoRA 权重而不是所有参数。这允许创建许多定制模型，这些模型可以在将预训练权重存储在 VRAM 中的机器上动态交换。与完全微调相比⁵，我们还观察到 GPT-3 175B 训练期间的速度提高了 25%，因为我们不需要计算绝大多数参数的梯度。

 LoRA 也有其局限性。例如，如果选择将 $A$ 和 $B$ 吸收到 $W$ 中以消除额外的推理延迟，则无法直接在一次前向传递中将输入批量处理到具有不同 $A$ 和 $B$ 的不同任务。不过，在延迟不重要的场景中，可以不合并权重并动态选择要批量处理的 LoRA 模块。

⁴ 我们在部署时仍然需要 350GB 的型号；而存储 100 个适配型号只需要 $350GB+35MB\ast 100\approx 354GB$，而不是 $100\ast 350GB\approx 35TB$。
⁵ 对于 GPT-3 175B，完全微调的训练吞吐量为每个 V100 GPU 32.5 tokens/s；使用相同数量的权重分片来实现模型并行性，LoRA 的吞吐量为每个 V100 GPU 43.1 tokens/s。

5. 实证实验

 在扩展到 GPT-3 175B（Brown 等人，2020）之前，我们评估了 LoRA 在 RoBERTa (Liu et al., 2019)、DeBERTa (He et al., 2021) 和 GPT-2 (Radford et al., b) 上的下游任务表现。我们的实验涵盖了从自然语言理解（NLU）到生成（NLG）的广泛任务。具体来说，我们在 GLUE (Wang et al., 2019) 基准上对 RoBERTa 和 DeBERTa 进行了评估。我们遵循 Li & Liang (2021) 在 GPT-2 上的设置进行直接比较，并添加 WikiSQL (Zhong et al., 2017)（NL 到 SQL 查询）和 SAMSum (Gliwa et al, 2019)（对话摘要）在 GPT-3 上进行大规模实验。有关我们使用的数据集的更多详细信息，请参阅附录 C。我们在所有实验中均使用 NVIDIA Tesla V100。

5.1 基线

 为了与其他基线进行广泛的比较，我们复制了先前工作中使用的设置，并尽可能重复使用它们报告的数字。然而，这意味着某些基线可能只出现在某些实验中。

 微调（Fine-Tuning，FT） 是一种常见的适应（adaptation）方法。在微调过程中，模型被初始化为预先训练的权重和偏差，并且所有模型参数都经历梯度更新。一个简单的变体是只更新一些层，而冻结其他层。我们在 GPT-2 的先前工作 (Li & Liang, 2021) 中包括了一个这样的基线，它只适应最后两层（${\mathbf{FT}}^{Top2}$）。

 Bias-only 或 BitFit 是一种基线，我们只训练偏差向量，同时冻结其他所有内容。同时，BitFit (Zaken et al., 2021) 也研究了这种基线。

 前缀嵌入调整（Prefix-embedding tuning，PreEmbed） 在输入标记中插入特殊标记。这些特殊标记具有可训练的词嵌入，通常不在模型的词汇表中。将这些标记放在哪里会影响性能。我们专注于“前缀”，将此类标记添加到提示前面，以及 “中缀（prefixing）”，将其附加到提示后面；两者都在 Li & Liang (2021) 中进行了讨论。我们使用 $l_p$（resp. $l_i$）表示前缀（prefix，resp. infix）标记的数量。可训练参数的数量为 $|\Theta |=d_{model}\times \left(l_p+l_i\right)$。

 前缀层调整（Prefix-layer tuning，PreLayer） 是前缀嵌入调整的扩展。我们学习每个 Transformer 层之后的激活，而不是仅仅学习某些特殊 token 的词嵌入（或者说，嵌入层之后的激活）。从前几层计算出的激活被可训练的激活所取代。由此产生的可训练参数数量为 $|\Theta |=L\times d_{model}\times \left(l_p+l_i\right)$，其中 $L$ 是 Transformer 层的数量。

 Houlsby et al. (2019) 提出的适配器调整（Adapter tuning） 在自注意力模块（和 MLP 模块）和后续残差连接之间插入适配器层。适配器层中有两个带偏差的全连接层，中间有一个非线性。我们将这种原始设计称为 ${\mathbf{Adapter}}^{\mathbf{H}}$。最近，Lin et al. (2020) 提出了一种更有效的设计，适配器层仅在 MLP 模块之后和 LayerNorm 之后应用。我们称之为 ${\mathbf{Adapter}}^{\mathbf{L}}$。这与 Pfeiffer et al. (2021) 提出的另一种设计非常相似，我们将其称为 ${\mathbf{Adapter}}^{\mathbf{P}}$。我们还包括另一个基线调用 AdapterDrop (Ruckl ¨ e et al., 2020)，它删除了一些适配器层以提高效率（${\mathbf{Adapter}}^{\mathbf{D}}$）。我们尽可能引用先前工作中的数字，以最大化我们与之比较的基线数量；它们位于第一列带有星号（$\ast$）的行中。在所有情况下，我们有 $|\Theta |={\hat{L}}_{Adpt}\times \left(2\times d_{model}\times r+r+d_{model}\right)+2\times {\hat{L}}_{LN}\times d_{model}$，其中 ${\hat{L}}_{Adpt}$ 是适配器层的数量，${\hat{L}}_{LN}$ 是可训练 LayerNorms 的数量（例如，在 ${\mathrm{Adapter}}^L$ 中）。

 LoRA 将可训练的秩分解矩阵对与现有权重矩阵并行添加。如第 4.2 节所述，为了简单起见，我们在大多数实验中仅将 LoRA 应用于 $W_q$ 和 $W_v$。可训练参数的数量由秩 $r$ 和原始权重的形状决定：$|\Theta |=2\times {\hat{L}}_{LoRA}\times d_{model}\times r$，其中 ${\hat{L}}_{LoRA}$ 是我们将 LoRA 应用于的权重矩阵的数量。

5.2 ROBERTA BASE/LARGE

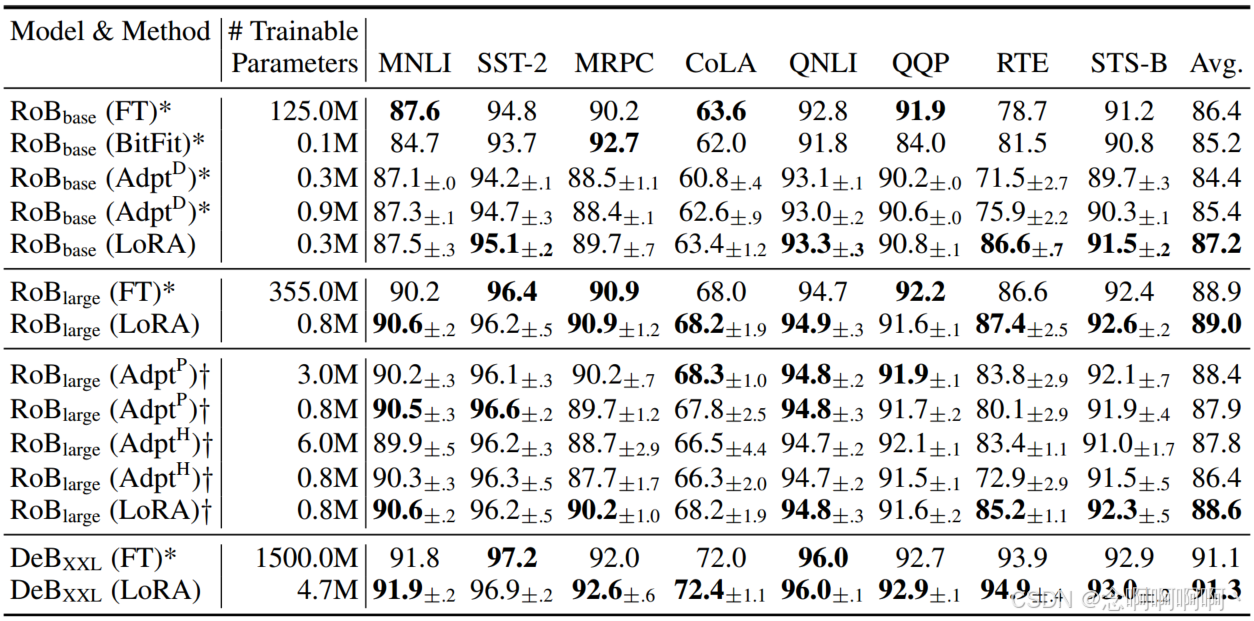
 RoBERTa (Liu et al., 2019) 优化了 BERT (Devlin et al., 2019a) 中最初提出的预训练方案，并在不引入更多可训练参数的情况下提升了后者的任务性能。尽管近年来 RoBERTa 在 GLUE 基准 (Wang et al., 2019) 等 NLP 排行榜上已经被更大的模型超越，但就其规模而言，它在从业者中仍然是一种具有竞争力且受欢迎的预训练模型。我们从 HuggingFace Transformers 库 (Wolf et al., 2020) 中获取预训练的 RoBERTa 基础（125M）和 RoBERTa 大型（355M），并评估不同高效自适应方法在 GLUE 基准任务上的表现。我们还根据他们的设置复制了 Houlsby et al. (2019) 和 Pfeiffer et al. (2021) 的模型。为了确保公平比较，我们在与适配器进行比较时对 LoRA 的评估方式进行了两项重要更改。首先，我们对所有任务使用相同的批处理大小，并使用 128 的序列长度来匹配适配器基线。其次，我们将模型初始化为针对 MRPC、RTE 和 STS-B 的预训练模型，而不是像微调基线那样已经适应 MNLI 的模型。遵循 Houlsby et al. (2019) 的这种更受限制的设置的运行标记为 $y$。结果显示在表 2（前三个部分）中。有关使用的超参数的详细信息，请参见第 D.1 节。

5.3 DEBERTA XXL

 DeBERTa (He et al., 2021) 是 BERT 的一个较新的变体，它在更大规模上进行了训练，并且在 GLUE (Wang et al., 2019) 和 SuperGLUE (Wang et al., 2020) 等基准测试中表现非常出色。我们评估了 LoRA 是否仍能在 GLUE 上与完全微调的 DeBERTa XXL（1.5B）的性能相匹配。结果显示在表 2（底部部分）中。有关使用的超参数的详细信息，请参见第 D.2 节。

5.4 GPT-2 MEDIUM/LARGE

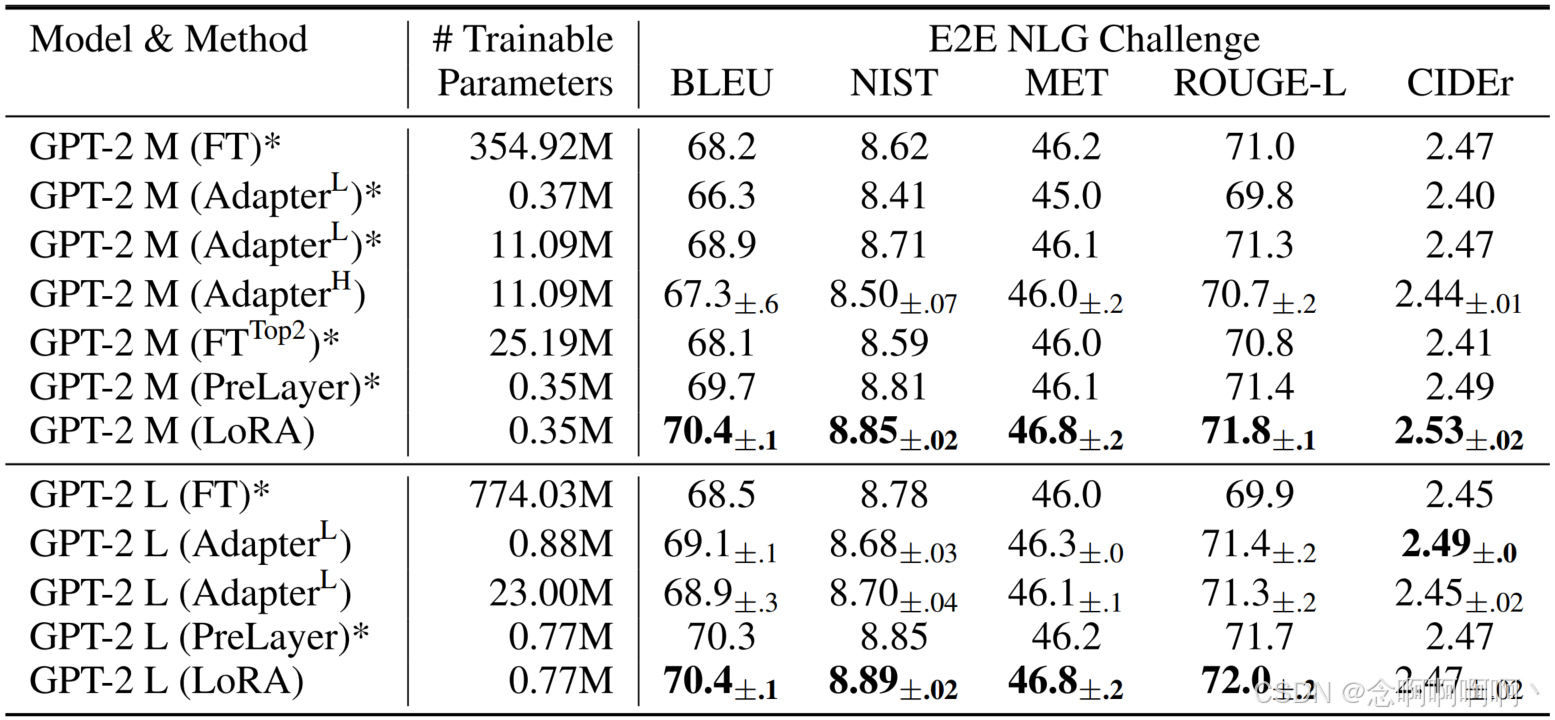
 我们已经证明 LoRA 可以成为 NLU 上完全微调的有力替代方案，我们希望回答 LoRA 是否仍然在 NLG 模型上占主导地位，例如 GPT-2 中型和大型模型 (Radford et al., b)。为了进行直接比较，我们将设置尽可能接近 Li & Liang (2021)。由于篇幅限制，我们仅在本节中展示我们在 E2E NLG 挑战赛上的结果（表 3）。有关 WebNLG (Gardent et al., 2017) 和 DART (Nan et al., 2020) 的结果，请参见 F.1 节。我们在 D.3 节中列出了使用的超参数。

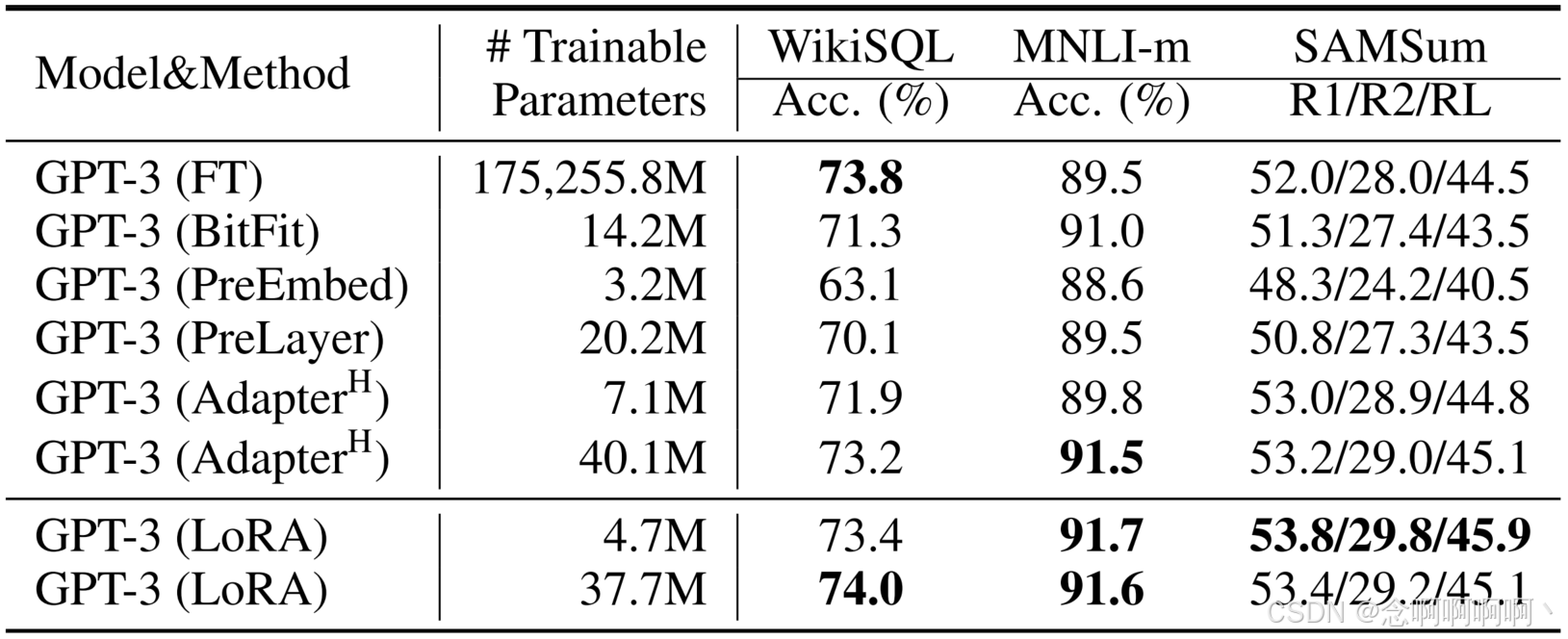
5.5 扩展到 GPT-3 175B

 作为 LoRA 的最终压力测试，我们扩展到具有 1750 亿个参数的 GPT-3。由于训练成本高，我们仅报告给定任务在随机种子上的典型标准差，而不是为每个条目提供一个标准差。有关使用的超参数的详细信息，请参阅第 D.4 节。

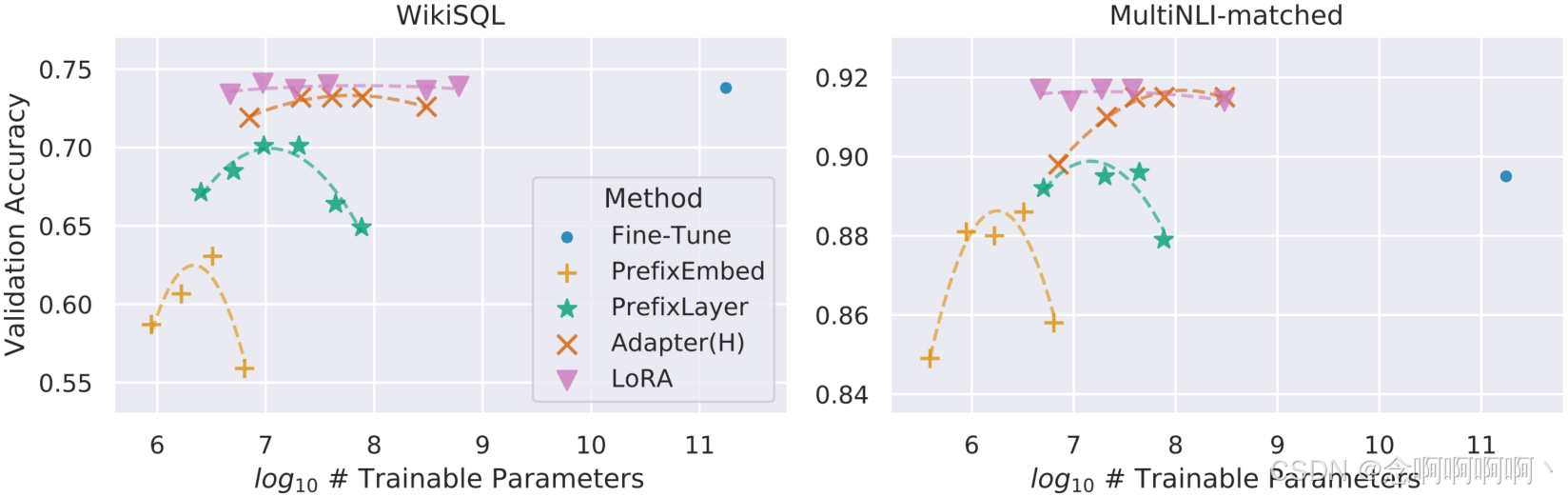
 如表 4 所示，LoRA 在所有三个数据集上都达到或超过了微调基线。请注意，并非所有方法都能从拥有更多可训练参数中单调受益，如图 2 所示。当我们使用超过 256 个特殊标记进行前缀嵌入调整或使用超过 32 个特殊标记进行前缀层调整时，我们观察到性能显着下降。这证实了 Li & Liang (2021) 中的类似观察结果。虽然对这种现象的彻底调查超出了这项工作的范围，但我们怀疑拥有更多特殊标记会导致输入分布进一步偏离训练前数据分布。另外，我们将在 F.3 节中研究不同适应方法在低数据状态下的性能。

6. 相关作品

 Transformer 语言模型。Transformer (Vaswani et al., 2017) 是一种大量使用自注意力机制的序列到序列架构。Radford et al. (a) 通过使用 Transformer 解码器堆栈将其应用于自回归语言建模。从那时起，基于 Transformer 的语言模型就主导了 NLP，在许多任务中取得了最先进的成果。BERT (Devlin et al., 2019b) 和 GPT-2 (Radford et al., b) 带来了一种新范式——两者都是在大量文本上训练的大型 Transformer 语言模型——在通用领域数据上进行预训练后，在特定于任务的数据上进行微调，与直接在特定于任务的数据上进行训练相比，可以显着提高性能。训练更大的 Transformer 通常可以获得更好的性能，并且仍然是一个活跃的研究方向。 GPT-3 (Brown et al., 2020) 是迄今为止训练的最大的单一 Transformer 语言模型，具有 175B 个参数。

 提示工程（Prompt Engineering）和微调。虽然 GPT-3 175B 只需几个额外的训练示例就可以调整其行为，但结果在很大程度上取决于输入提示 (Brown et al., 2020)。这需要一种编写和格式化提示的经验艺术，以最大限度地提高模型在所需任务上的性能，这被称为快速工程或快速黑客攻击。微调将预先在一般领域训练过的模型重新训练到特定任务 Devlin et al. (2019b); Radford et al. (a)。它的变体包括仅学习参数的子集 Devlin et al. (2019b); Collobert & Weston (2008)，但从业者通常会重新训练所有参数以最大化下游性能。然而，由于 GPT-3 175B 的庞大规模，它产生的检查点很大，而且与预训练具有相同的内存占用，因此硬件进入门槛较高，这给以通常的方式进行微调带来了挑战。

 参数高效自适应。许多人提议在神经网络的现有层之间插入适配器层 (Houlsby et al., 2019; Rebuffi et al., 2017; Lin et al., 2020)。我们的方法使用类似的瓶颈结构对权重更新施加低秩约束。关键的功能差异在于，我们学习到的权重可以在推理过程中与主权重合并，因此不会引入任何延迟，而适配器层则不会出现这种情况（第 3 节）。适配器的临时扩展是 COMPACTER (Mahabadi et al., 2021)，它本质上使用 Kronecker 积和一些预定的权重共享方案来参数化适配器层。同样，将 LoRA 与其他基于张量积的方法相结合可能会提高其参数效率，我们将此留待将来研究。最近，许多人提出优化输入词嵌入来代替微调，类似于提示工程的连续和可微分泛化 (Li & Liang, 2021; Lester et al., 2021; Hambardzumyan et al., 2020; Liu et al., 2021)。我们在实验部分中包括与 Li & Liang (2021) 的比较。然而，这一系列工作只能通过在提示中使用更多特殊标记来扩大规模，当学习位置嵌入时，这些标记会占用任务标记的可用序列长度。

 深度学习中的低秩结构。低秩结构在机器学习中非常常见。许多机器学习问题都具有一定的内在低秩结构 (Li et al., 2016; Cai et al., 2010; Li et al., 2018b; Grasedyck et al., 2013)。此外，众所周知，对于许多深度学习任务，尤其是那些具有严重过度参数化的神经网络的任务，学习到的神经网络在训练后将具有低秩特性 (Oymak et al., 2019)。一些先前的研究甚至在训练原始神经网络时明确施加了低秩约束 (Sainath et al., 2013; Povey et al., 2018; Zhang et al., 2014; Jaderberg et al., 2014; Zhao et al., 2016; Khodak et al., 2021; Denil et al., 2014)；然而，据我们所知，这些工作都没有考虑对冻结模型进行低秩更新以适应下游任务。在理论文献中，众所周知，当底层概念类别具有某些低秩结构时 (Allen-Zhu et al., 2019; Li & Liang, 2018)，神经网络的表现优于其他经典学习方法，包括相应的（有限宽度）神经切线核 (Ghorbani et al, 2020; Allen-Zhu & Li, 2019; Allen-Zhu & Li, 2020a)。Allen-Zhu & Li (2020b) 中的另一个理论结果表明，低秩适应可用于对抗性训练。总之，我们认为我们提出的低秩适应更新得到了文献的充分启发。

7. 理解低秩更新

 鉴于 LoRA 的经验优势，我们希望进一步解释从下游任务中学习到的低秩适应的特性。请注意，低秩结构不仅降低了硬件进入门槛，使我们能够并行运行多个实验，而且还能更好地解释更新权重与预训练权重之间的关联。我们的研究重点是 GPT-3 175B，我们在其中实现了可训练参数的最大减少（高达 10,000 倍），而不会对任务性能产生不利影响。

 我们进行了一系列实证研究来回答以下问题：1) 给定一个参数预算约束，我们应该调整预训练 Transformer 中的哪个权重矩阵子集以最大化下游性能？2) “最优（optimal）” 自适应矩阵 $∆W$ 真的是秩不足的吗？如果是这样，那么在实践中使用什么等级比较好？3) ∆W 和 W 之间有什么联系？$∆W$ 与 $W$ 高度相关吗？$∆W$ 与 $W$ 相比有多大？

 我们相信，我们对问题 (2) 和 (3) 的回答阐明了使用预训练语言模型执行下游任务的基本原理，这是 NLP 中的一个关键主题。

7.1 我们应该将 LORA 应用于 Transformer 中的哪些权重矩阵？

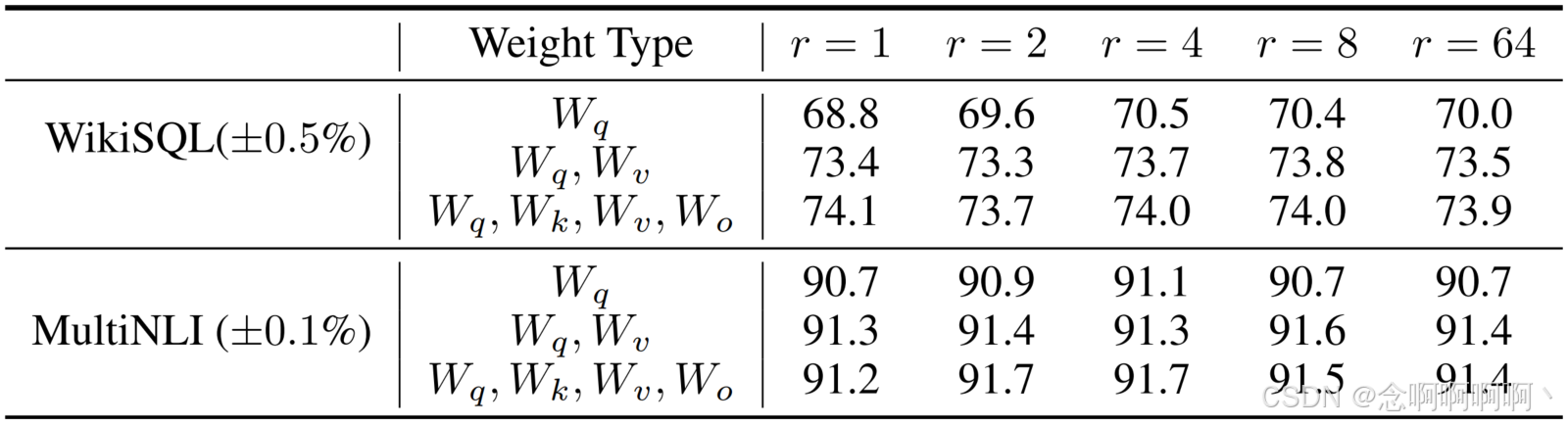
 在参数预算有限的情况下，我们应该使用 LoRA 调整哪些类型的权重才能在下游任务中获得最佳性能？如第 4.2 节所述，我们仅考虑自注意力模块中的权重矩阵。我们在 GPT-3 175B 上设置了 18M（如果存储在 FP16 中则大约为 35MB）的参数预算，对于所有 96 个层，如果我们调整一种类型的注意力权重，则对应于 $r=8$，如果我们调整两种类型，则对应于 $r=4$。结果如表 5 所示。

 请注意，将所有参数放入 $∆W_q$ 或 $∆W_k$ 中会导致性能显著降低，而同时调整 $W_q$ 和 $W_v$ 可获得最佳结果。这表明，即使秩为 4，$∆W$ 中的信息量也足够大，因此调整更多权重矩阵比调整单一类型的秩较大的权重更好。

7.2 LORA 的最佳等级 $r$ 是多少？

 我们将注意力转向等级 $r$ 对模型性能的影响。我们调整了 { W q ,   W v } \left\{W_q,\ W_v\right\} {Wq​, Wv​}， { W q ,   W k ,   W v ,   W c } \left\{W_q,\ W_k,\ W_v,\ W_c\right\} {Wq​, Wk​, Wv​, Wc​} 和 $W_q$ 进行比较。

 表 6 表明，令人惊讶的是，LoRA 在 $r$ 非常小的情况下就已经具有竞争力（ { W q ,   W v } \left\{W_q,\ W_v\right\} {Wq​, Wv​} 的表现优于 $W_q$）。这表明更新矩阵 $∆W$ 可能具有非常小的 “固有秩（intrinsic rank）”。⁶为了进一步支持这一发现，我们检查了通过不同的 $r$ 选择和不同的随机种子学习到的子空间的重叠。我们认为增加 $r$ 并不能覆盖更有意义的子空间，这表明低秩自适应矩阵就足够了。

⁶ 然而，我们并不期望一个小的 $r$ 对每个任务或数据集都有效。考虑以下思想实验:如果下游任务使用的语言与用于预训练的语言不同，则重新训练整个模型（类似于 $r=d_{model}$）的 LoRA 肯定可以优于 $r$ 较小的 LoRA。

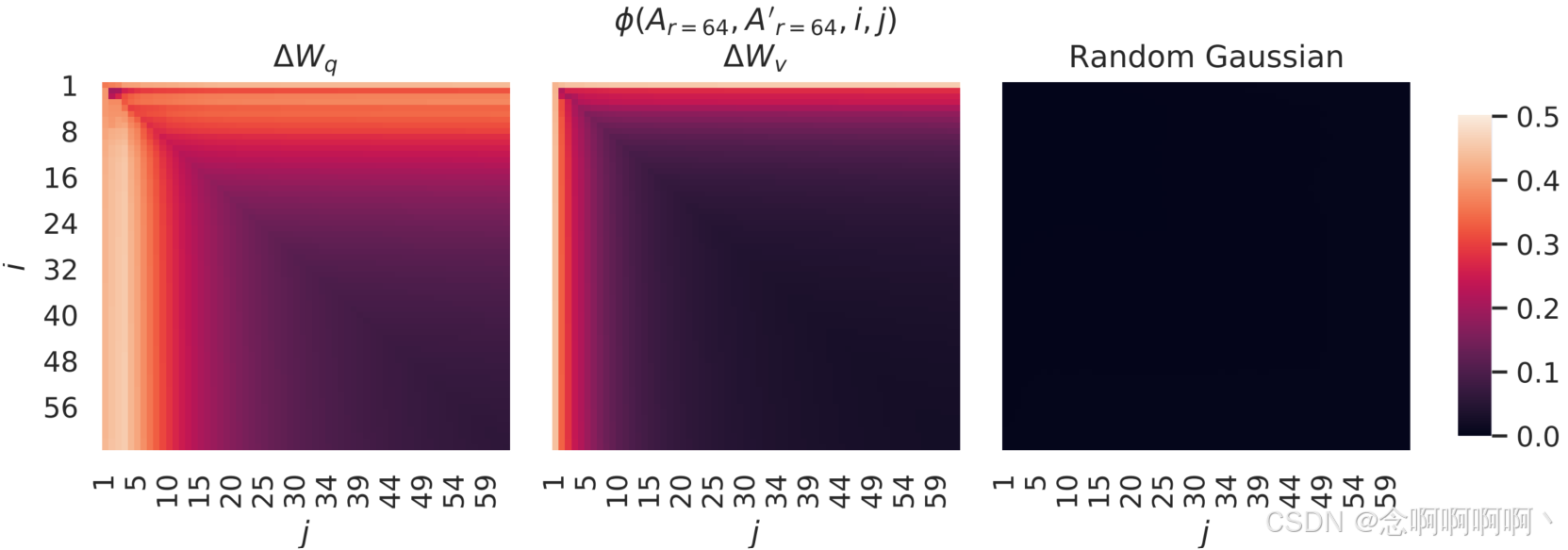
 不同 $r$ 之间的子空间相似性。给定 $A_{r=8}$ 和 $A_{r=64}$，它们是使用相同预训练模型学习到的秩为 $r=8$ 和 $64$ 的自适应矩阵，我们执行奇异值分解并获得右奇异酉矩阵（right-singular unitary matrices） $U_{A_{r=8}}$ 和 $U_{A_{r=64}}$。⁷我们希望回答：$U_{A_{r=8}}$ 中前 $i$ 个奇异向量所占子空间（对于 $1\le i\le 8$）中有多少包含在 $U_{A_{r=64}}$ 中前 $j$ 个奇异向量所占子空间（对于 $1\le j\le 64$）中？我们使用基于 Grassmann 距离的归一化子空间相似性来测量这个量（有关更正式的讨论，请参阅附录 G）

 其中 $U_{Ar}^i=8$ 表示 $U_{A_{r=8}}$ 中与前 $i$ 个奇异向量相对应的列。

⁷ 注意，类似的分析可以用B和左奇异酉矩阵进行——我们坚持用 $A$ 进行实验。

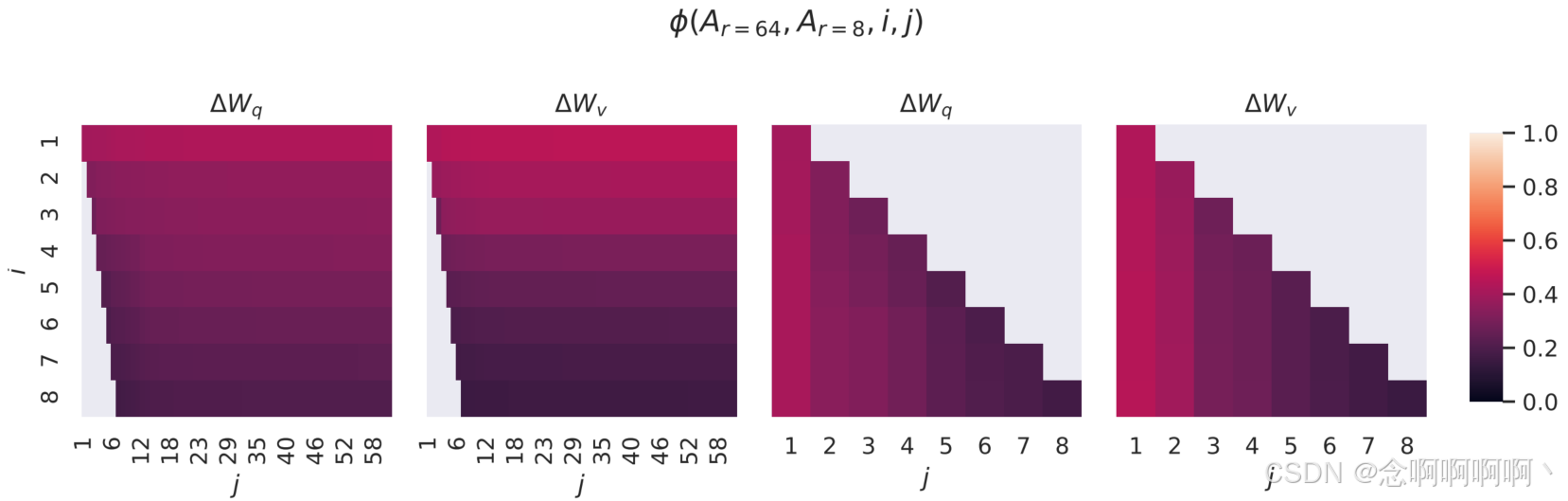
 $\varphi \left(\cdot \right)$ 的范围为 $[0;1]$，其中 1 表示子空间完全重叠，0 表示完全分离。参见图 3，了解 $\varphi$ 随着 $i$ 和 $j$ 的变化而如何变化。由于空间限制，我们仅查看第 48 层（共 96 层），但结论也适用于其他层，如第 H.1 节所示。

 我们从图 3 中得出了一个重要的观察结果。

 对应于顶部奇异向量的方向在 $A_{r=8}$ 和 $A_{r=64}$ 之间有显著重叠，而其他方向则没有重叠。具体来说，$A_{r=8}$ 的 $∆W_v$（分别为 $∆W_q$）和 $A_{r=64}$ 的 $∆W_v$（分别为 $∆W_q$）共享一个维度为 1 的子空间，其归一化相似度 $>0.5$，这解释了为什么 $r=1$ 在我们的 GPT-3 下游任务中表现相当出色。

 由于 $A_{r=8}$ 和 $A_{r=64}$ 都是使用相同的预训练模型学习的，图 3 表明 $A_{r=8}$ 和 $A_{r=64}$ 的顶部奇异向量方向是最有用的，而其他方向可能主要包含训练期间积累的随机噪声。因此，自适应矩阵确实可以具有非常低的秩。

 不同随机种子之间的子空间相似性。我们通过绘制 $r=64$ 的两个随机种子运行之间的归一化子空间相似性来进一步证实这一点，如图 4 所示。$∆W_q$ 似乎比 $∆W_v$ 具有更高的 “内在秩（intrinsic rank）”，因为 $∆W_q$ 的两次运行都学习到了更多常见的奇异值方向，这与我们在表 6 中的经验观察一致。作为比较，我们还绘制了两个随机高斯矩阵，它们彼此之间没有任何共同的奇异值方向。

7.3 适应矩阵 $∆W$ 与 $W$ 相比如何？

 我们进一步研究了 $∆W$ 和 $W$ 之间的关系。具体来说，$∆W$ 是否与 $W$ 高度相关？（或者从数学上讲，$∆W$ 是否主要包含在 $W$ 的顶部奇异方向上？）此外，$∆W$ 与 $W$ 中其对应方向相比有多 “大（large）”？这可以揭示调整预训练语言模型的底层机制。

 为了回答这些问题，我们通过计算 $U^{⊺}{WV}^{⊺}$ 将 $W$ 投影到 $∆W$ 的 $r$ 维子空间上，其中 $U/V$ 是 $∆W$ 的左/右奇异向量矩阵。然后，我们比较 ${||U^{⊺}{WV}^{⊺}||}_F$ 和 ${||W||}_F$ 之间的 Frobenius 范数。为了进行比较，我们还通过将 $U,V$ 替换为 $W$ 的前 $r$ 个奇异向量或随机矩阵来计算 ${||U^{⊺}{WV}^{⊺}||}_F$。

 我们从表 7 中得出几个结论。首先，与随机矩阵相比，$∆W$ 与 $W$ 具有更强的相关性，这表明 $∆W$ 放大了 $W$ 中已经存在的一些特征。其次，$∆W$ 不会重复 $W$ 的顶部奇异方向，而是仅放大 $W$ 中未强调的方向。第三，放大因子相当大：当 $r=4$ 时，$21.5\approx 6.91=0.32$。有关为什么 $r=64$ 具有较小的放大因子，请参见第 H.4 节。我们还在第 H.3 节中提供了可视化效果，展示了当我们从 $W_q$ 中包含更多顶部奇异方向时相关性如何变化。这表明低秩适应矩阵可能会放大在一般预训练模型中学习到但未强调的特定下游任务的重要特征。

8. 结论和未来工作

 就所需硬件以及为不同任务托管独立实例的存储/切换成本而言，对庞大的语言模型进行微调的成本过高。我们提出了 LoRA，这是一种高效的自适应策略，既不会引入推理延迟，也不会减少输入序列长度，同时保持较高的模型质量。重要的是，通过共享绝大多数模型参数，它可以在部署为服务时实现快速任务切换。虽然我们专注于 Transformer 语言模型，但提出的原则通常适用于任何具有密集层的神经网络。

 未来的研究方向有很多。1) LoRA 可以与其他有效的自适应方法相结合，从而可能提供正交改进。2) 微调或 LoRA 背后的机制尚不明确——在预训练期间学习的特征如何转化为在下游任务中表现良好？我们相信 LoRA 比完全微调更容易回答这个问题。3) 我们主要依靠启发式方法来选择应用 LoRA 的权重矩阵。有没有更原则性的方法来做到这一点？4) 最后，$∆W$ 的秩亏（rank-deficiency）表明 $W$ 也可能是秩亏的，这也可以成为未来研究的灵感来源。

参考文献

Armen Aghajanyan, Luke Zettlemoyer, and Sonal Gupta. Intrinsic Dimensionality Explains the Effectiveness of Language Model Fine-Tuning. arXiv:2012.13255 [cs], December 2020. URL http://arxiv.org/abs/2012.13255.
Zeyuan Allen-Zhu and Yuanzhi Li. What Can ResNet Learn Efficiently, Going Beyond Kernels? In NeurIPS, 2019. Full version available at http://arxiv.org/abs/1905.10337.
Zeyuan Allen-Zhu and Yuanzhi Li. Backward feature correction: How deep learning performs deep learning. arXiv preprint arXiv:2001.04413, 2020a.
Zeyuan Allen-Zhu and Yuanzhi Li. Feature purification: How adversarial training performs robust deep learning. arXiv preprint arXiv:2005.10190, 2020b.
Zeyuan Allen-Zhu, Yuanzhi Li, and Zhao Song. A convergence theory for deep learning via overparameterization. In ICML, 2019. Full version available at http://arxiv.org/abs/1811.03962.
Jimmy Lei Ba, Jamie Ryan Kiros, and Geoffrey E. Hinton. Layer normalization, 2016.
Tom B. Brown, Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared Kaplan, Prafulla Dhariwal, Arvind Neelakantan, Pranav Shyam, Girish Sastry, Amanda Askell, Sandhini Agarwal, Ariel Herbert-Voss, Gretchen Krueger, Tom Henighan, Rewon Child, Aditya Ramesh, Daniel M. Ziegler, Jeffrey Wu, Clemens Winter, Christopher Hesse, Mark Chen, Eric Sigler, Mateusz Litwin, Scott Gray, Benjamin Chess, Jack Clark, Christopher Berner, Sam McCandlish, Alec Radford, Ilya Sutskever, and Dario Amodei. Language Models are Few-Shot Learners. arXiv:2005.14165 [cs], July 2020. URL http://arxiv.org/abs/2005.14165.
Jian-Feng Cai, Emmanuel J Candes, and Zuowei Shen. A singular value thresholding algorithm for ` matrix completion. SIAM Journal on optimization, 20(4):1956–1982, 2010.
Daniel Cer, Mona Diab, Eneko Agirre, Inigo Lopez-Gazpio, and Lucia Specia. Semeval-2017 task 1: Semantic textual similarity multilingual and crosslingual focused evaluation. Proceedings of the 11th International Workshop on Semantic Evaluation (SemEval-2017), 2017. doi: 10.18653/ v1/s17-2001. URL http://dx.doi.org/10.18653/v1/S17-2001.
Ronan Collobert and Jason Weston. A unified architecture for natural language processing: deep neural networks with multitask learning. In Proceedings of the 25th international conference on Machine learning, ICML ’08, pp. 160–167, New York, NY, USA, July 2008. Association for Computing Machinery. ISBN 978-1-60558-205-4. doi: 10.1145/1390156.1390177. URL https://doi.org/10.1145/1390156.1390177.
Misha Denil, Babak Shakibi, Laurent Dinh, Marc’Aurelio Ranzato, and Nando de Freitas. Predicting parameters in deep learning, 2014.
Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. Bert: Pre-training of deep bidirectional transformers for language understanding, 2019a.
Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. arXiv:1810.04805 [cs], May 2019b. URL http://arxiv.org/abs/1810.04805. arXiv: 1810.04805.
William B. Dolan and Chris Brockett. Automatically constructing a corpus of sentential paraphrases. In Proceedings of the Third International Workshop on Paraphrasing (IWP2005), 2005. URL https://aclanthology.org/I05-5002.
Claire Gardent, Anastasia Shimorina, Shashi Narayan, and Laura Perez-Beltrachini. The webnlg challenge: Generating text from rdf data. In Proceedings of the 10th International Conference on Natural Language Generation, pp. 124–133, 2017.
Behrooz Ghorbani, Song Mei, Theodor Misiakiewicz, and Andrea Montanari. When do neural networks outperform kernel methods? arXiv preprint arXiv:2006.13409, 2020.
Bogdan Gliwa, Iwona Mochol, Maciej Biesek, and Aleksander Wawer. Samsum corpus: A humanannotated dialogue dataset for abstractive summarization. CoRR, abs/1911.12237, 2019. URL http://arxiv.org/abs/1911.12237.
Lars Grasedyck, Daniel Kressner, and Christine Tobler. A literature survey of low-rank tensor approximation techniques. GAMM-Mitteilungen, 36(1):53–78, 2013.
Jihun Ham and Daniel D. Lee. Grassmann discriminant analysis: a unifying view on subspace-based learning. In ICML, pp. 376–383, 2008. URL https://doi.org/10.1145/1390156.1390204.
Karen Hambardzumyan, Hrant Khachatrian, and Jonathan May. WARP: Word-level Adversarial ReProgramming. arXiv:2101.00121 [cs], December 2020. URL http://arxiv.org/abs/ 2101.00121. arXiv: 2101.00121.
Pengcheng He, Xiaodong Liu, Jianfeng Gao, and Weizhu Chen. Deberta: Decoding-enhanced bert with disentangled attention, 2021.
Neil Houlsby, Andrei Giurgiu, Stanislaw Jastrzebski, Bruna Morrone, Quentin de Laroussilhe, Andrea Gesmundo, Mona Attariyan, and Sylvain Gelly. Parameter-Efficient Transfer Learning for NLP. arXiv:1902.00751 [cs, stat], June 2019. URL http://arxiv.org/abs/1902.00751.
Max Jaderberg, Andrea Vedaldi, and Andrew Zisserman. Speeding up convolutional neural networks with low rank expansions. arXiv preprint arXiv:1405.3866, 2014.
Mikhail Khodak, Neil Tenenholtz, Lester Mackey, and Nicolo Fusi. Initialization and regularization of factorized neural layers, 2021.
Diederik P. Kingma and Jimmy Ba. Adam: A method for stochastic optimization, 2017.
Dmitry Lepikhin, HyoukJoong Lee, Yuanzhong Xu, Dehao Chen, Orhan Firat, Yanping Huang, Maxim Krikun, Noam Shazeer, and Zhifeng Chen. Gshard: Scaling giant models with conditional computation and automatic sharding, 2020.
Brian Lester, Rami Al-Rfou, and Noah Constant. The Power of Scale for Parameter-Efficient Prompt Tuning. arXiv:2104.08691 [cs], April 2021. URL http://arxiv.org/abs/2104.08691. arXiv: 2104.08691.
Chunyuan Li, Heerad Farkhoor, Rosanne Liu, and Jason Yosinski. Measuring the Intrinsic Dimension of Objective Landscapes. arXiv:1804.08838 [cs, stat], April 2018a. URL http: //arxiv.org/abs/1804.08838. arXiv: 1804.08838.
Xiang Lisa Li and Percy Liang. Prefix-Tuning: Optimizing Continuous Prompts for Generation. arXiv:2101.00190 [cs], January 2021. URL http://arxiv.org/abs/2101.00190.
Yuanzhi Li and Yingyu Liang. Learning overparameterized neural networks via stochastic gradient descent on structured data. In Advances in Neural Information Processing Systems, 2018.
Yuanzhi Li, Yingyu Liang, and Andrej Risteski. Recovery guarantee of weighted low-rank approximation via alternating minimization. In International Conference on Machine Learning, pp. 2358–2367. PMLR, 2016.
Yuanzhi Li, Tengyu Ma, and Hongyang Zhang. Algorithmic regularization in over-parameterized matrix sensing and neural networks with quadratic activations. In Conference On Learning Theory, pp. 2–47. PMLR, 2018b.
Zhaojiang Lin, Andrea Madotto, and Pascale Fung. Exploring versatile generative language model via parameter-efficient transfer learning. In Findings of the Association for Computational Linguistics: EMNLP 2020, pp. 441–459, Online, November 2020. Association for Computational Linguistics. doi: 10.18653/v1/2020.findings-emnlp.41. URL https://aclanthology. org/2020.findings-emnlp.41.
Xiao Liu, Yanan Zheng, Zhengxiao Du, Ming Ding, Yujie Qian, Zhilin Yang, and Jie Tang. GPT Understands, Too. arXiv:2103.10385 [cs], March 2021. URL http://arxiv.org/abs/ 2103.10385. arXiv: 2103.10385.
Yinhan Liu, Myle Ott, Naman Goyal, Jingfei Du, Mandar Joshi, Danqi Chen, Omer Levy, Mike Lewis, Luke Zettlemoyer, and Veselin Stoyanov. Roberta: A robustly optimized bert pretraining approach, 2019.
Ilya Loshchilov and Frank Hutter. Decoupled weight decay regularization. arXiv preprint arXiv:1711.05101, 2017.
Ilya Loshchilov and Frank Hutter. Decoupled weight decay regularization, 2019.
Rabeeh Karimi Mahabadi, James Henderson, and Sebastian Ruder. Compacter: Efficient low-rank hypercomplex adapter layers, 2021.
Linyong Nan, Dragomir Radev, Rui Zhang, Amrit Rau, Abhinand Sivaprasad, Chiachun Hsieh, Xiangru Tang, Aadit Vyas, Neha Verma, Pranav Krishna, et al Dart: Open-domain structured data record to text generation. arXiv preprint arXiv:2007.02871, 2020.
Jekaterina Novikova, Ondˇrej Dusek, and Verena Rieser. The e2e dataset: New challenges for end- ˇ to-end generation. arXiv preprint arXiv:1706.09254, 2017.
Samet Oymak, Zalan Fabian, Mingchen Li, and Mahdi Soltanolkotabi. Generalization guarantees for neural networks via harnessing the low-rank structure of the jacobian. arXiv preprint arXiv:1906.05392, 2019.
Jonas Pfeiffer, Aishwarya Kamath, Andreas Ruckl ¨ e, Kyunghyun Cho, and Iryna Gurevych. Adapter- ´ fusion: Non-destructive task composition for transfer learning, 2021.
Daniel Povey, Gaofeng Cheng, Yiming Wang, Ke Li, Hainan Xu, Mahsa Yarmohammadi, and Sanjeev Khudanpur. Semi-orthogonal low-rank matrix factorization for deep neural networks. In Interspeech, pp. 3743–3747, 2018.
Alec Radford, Karthik Narasimhan, Tim Salimans, and Ilya Sutskever. Improving Language Understanding by Generative Pre-Training. pp. 12, a.
Alec Radford, Jeffrey Wu, Rewon Child, David Luan, Dario Amodei, and Ilya Sutskever. Language Models are Unsupervised Multitask Learners. pp. 24, b.
Pranav Rajpurkar, Robin Jia, and Percy Liang. Know what you don’t know: Unanswerable questions for squad. CoRR, abs/1806.03822, 2018. URL http://arxiv.org/abs/1806.03822.
Sylvestre-Alvise Rebuffi, Hakan Bilen, and Andrea Vedaldi. Learning multiple visual domains with residual adapters. arXiv:1705.08045 [cs, stat], November 2017. URL http://arxiv.org/ abs/1705.08045. arXiv: 1705.08045.
Andreas Ruckl ¨ e, Gregor Geigle, Max Glockner, Tilman Beck, Jonas Pfeiffer, Nils Reimers, and ´ Iryna Gurevych. Adapterdrop: On the efficiency of adapters in transformers, 2020.
Tara N Sainath, Brian Kingsbury, Vikas Sindhwani, Ebru Arisoy, and Bhuvana Ramabhadran. Lowrank matrix factorization for deep neural network training with high-dimensional output targets. In 2013 IEEE international conference on acoustics, speech and signal processing, pp. 6655– 6659. IEEE, 2013.
Mohammad Shoeybi, Mostofa Patwary, Raul Puri, Patrick LeGresley, Jared Casper, and Bryan Catanzaro. Megatron-lm: Training multi-billion parameter language models using model parallelism, 2020.
Richard Socher, Alex Perelygin, Jean Wu, Jason Chuang, Christopher D. Manning, Andrew Ng, and Christopher Potts. Recursive deep models for semantic compositionality over a sentiment treebank. In Proceedings of the 2013 Conference on Empirical Methods in Natural Language Processing, pp. 1631–1642, Seattle, Washington, USA, October 2013. Association for Computational Linguistics. URL https://aclanthology.org/D13-1170.
Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, pp. 6000–6010, 2017.
Alex Wang, Amanpreet Singh, Julian Michael, Felix Hill, Omer Levy, and Samuel R. Bowman. Glue: A multi-task benchmark and analysis platform for natural language understanding, 2019.
Alex Wang, Yada Pruksachatkun, Nikita Nangia, Amanpreet Singh, Julian Michael, Felix Hill, Omer Levy, and Samuel R. Bowman. Superglue: A stickier benchmark for general-purpose language understanding systems, 2020.
Alex Warstadt, Amanpreet Singh, and Samuel R Bowman. Neural network acceptability judgments. arXiv preprint arXiv:1805.12471, 2018.
Adina Williams, Nikita Nangia, and Samuel Bowman. A broad-coverage challenge corpus for sentence understanding through inference. In Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long Papers), pp. 1112–1122, New Orleans, Louisiana, June 2018. Association for Computational Linguistics. doi: 10.18653/v1/N18-1101. URL https://www.aclweb.org/anthology/N18-1101.
Thomas Wolf, Lysandre Debut, Victor Sanh, Julien Chaumond, Clement Delangue, Anthony Moi, Pierric Cistac, Tim Rault, Remi Louf, Morgan Funtowicz, Joe Davison, Sam Shleifer, Patrick ´ von Platen, Clara Ma, Yacine Jernite, Julien Plu, Canwen Xu, Teven Le Scao, Sylvain Gugger, Mariama Drame, Quentin Lhoest, and Alexander M. Rush. Transformers: State-of-the-art natural language processing. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing: System Demonstrations, pp. 38–45, Online, October 2020. Association for Computational Linguistics. URL https://www.aclweb.org/anthology/ 2020.emnlp-demos.6.
Greg Yang and Edward J. Hu. Feature Learning in Infinite-Width Neural Networks. arXiv:2011.14522 [cond-mat], May 2021. URL http://arxiv.org/abs/2011.14522. arXiv: 2011.14522.
Elad Ben Zaken, Shauli Ravfogel, and Yoav Goldberg. Bitfit: Simple parameter-efficient fine-tuning for transformer-based masked language-models, 2021.
Yu Zhang, Ekapol Chuangsuwanich, and James Glass. Extracting deep neural network bottleneck features using low-rank matrix factorization. In 2014 IEEE international conference on acoustics, speech and signal processing (ICASSP), pp. 185–189. IEEE, 2014.
Yong Zhao, Jinyu Li, and Yifan Gong. Low-rank plus diagonal adaptation for deep neural networks. In 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 5005–5009. IEEE, 2016.
Victor Zhong, Caiming Xiong, and Richard Socher. Seq2sql: Generating structured queries from natural language using reinforcement learning. CoRR, abs/1709.00103, 2017. URL http:// arxiv.org/abs/1709.00103.