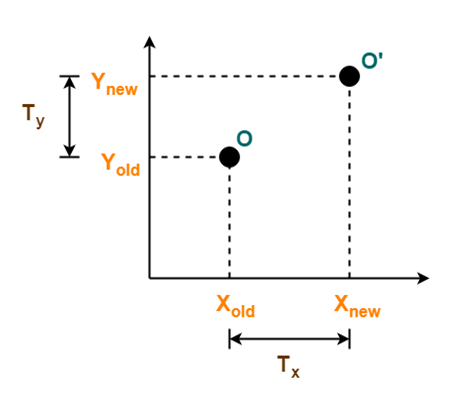
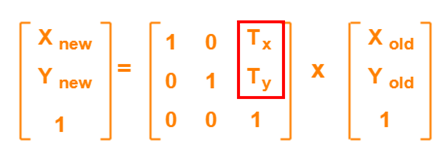
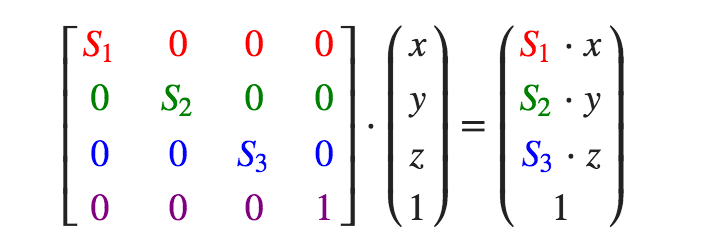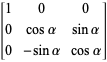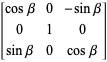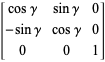向量的平移,比较简单。
- Xnew = Xold + Tx
- Ynew = Yold + Ty
缩放也较为简单
矩阵如何进行计算呢?之前的文章中有简介一种方法,把行旋转一下,然后与右侧对应相乘。在谷歌图片搜索旋转矩阵时,看到这张动图,觉得表述的很清晰了。
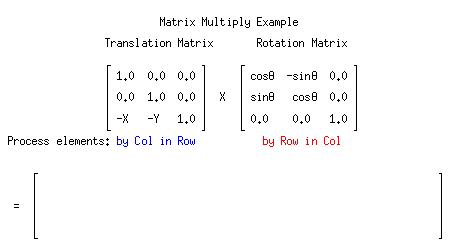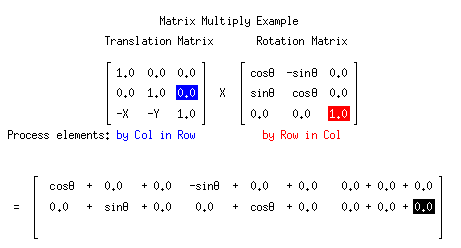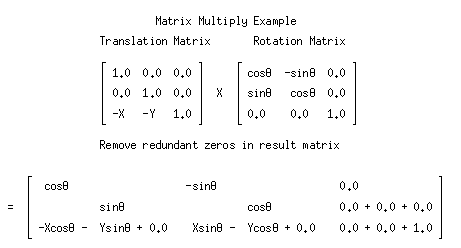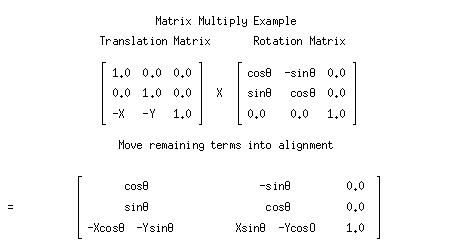
稍微复杂一点的是旋转,如果只是二维也很简单(因为很直观),但因为是三维的,有xyz三个轴,先推导二维的再延伸到三维。
YouTube上有很好的推导过程,视频链接地址(需穿.墙) https://www.youtube.com/watch?v=8XRvpDhTJpw
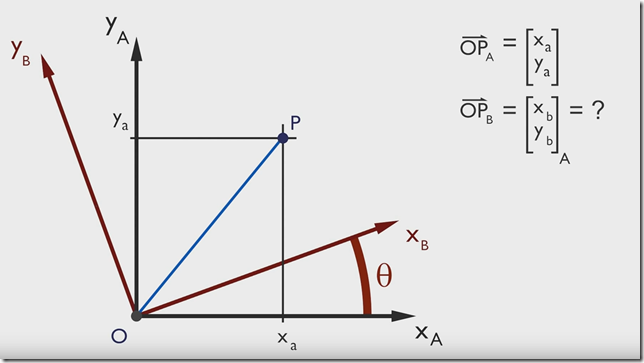
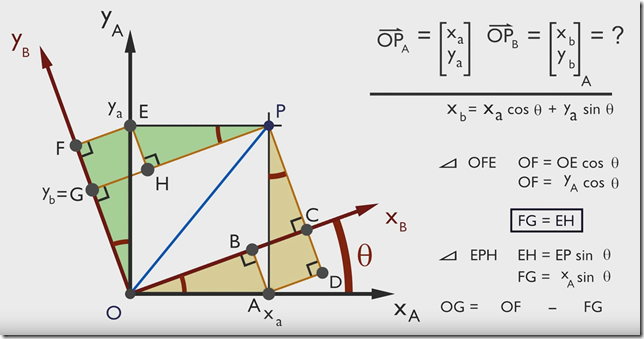
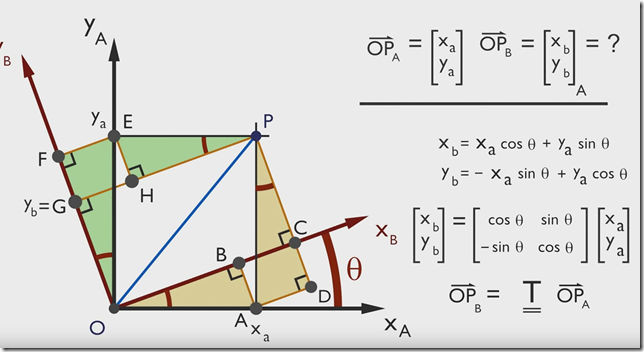
有点P(Xa,Ya),当坐标由 x –> y 旋转 θ 度后,求该点在新坐标轴的坐标是多少
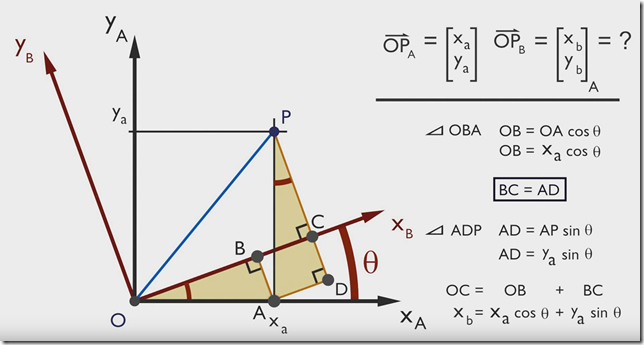
所以对于二维旋转来讲,旋转矩阵就是
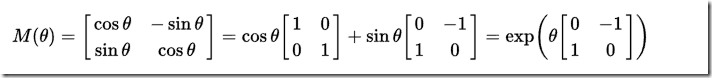
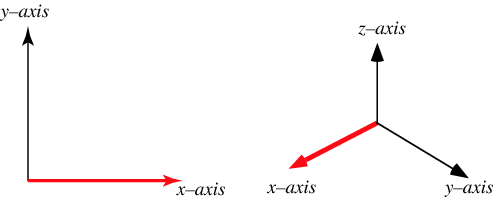
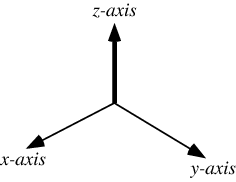
三维旋转,需要先搞清楚正、负方向(使用的是右手法则,在二维平面增加一维z,它的正方向朝向屏幕外)。
绕x轴进行旋转(在yz平面顺时针旋转)
绕y轴进行旋转(在zx平面顺时针旋转)
绕z轴进行旋转(在xy平面顺时针旋转)
— 图片来源:Rotation Matrix -- from Wolfram MathWorld
参考:https://zh.wikipedia.org/wiki/旋转矩阵
了解这些有什么用处呢?之前有讲到渲染被分为三个阶段:应用 –> 几何 –> 栅格化,其中几何阶段做了大量的变换工作。
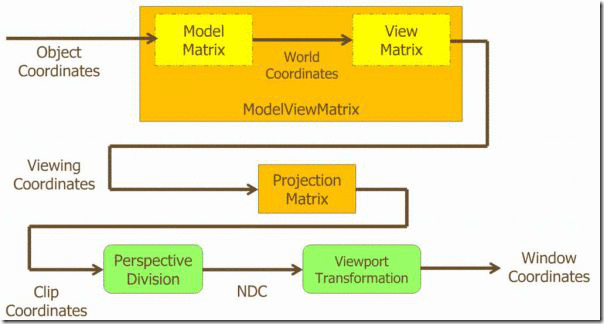
模型空间 –>( 模型矩阵) –> 世界空间 –> (视图矩阵) –> 观察空间(摄像机,右手坐标系,其余均采用左手) –> (投影矩阵) –> 裁剪空间 –> 屏幕空间,每一次变换都对应着相应的矩阵。
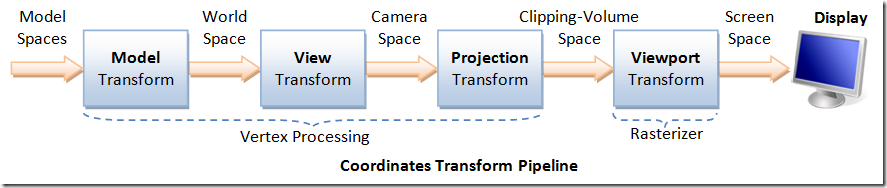
而Unity中的 UNITY_MATRIX_MVP 矩阵表示的是从模型到裁剪坐标的矩阵变换,Model Matrix ● View Matrix ● Projection Matrix。在Unity2017中使用 UnityObjectToClipPos 进行了替换,MVP也即是 模型(M)、视图(V)、透视(P)三个单词的首字母简写。
了解上面这些,才更容易理解Unity内置的变换矩阵
| 变量名 | 描述 |
| UNITY_MATRIX_MVP | 当前的模型观察投影矩阵,用于将顶点/方向矢量从模型空间变换到裁剪空间 |
| UNITY_MATRIX_MV | 当前的模型观察矩阵,用于将顶点/方向矢量从模型空间变换到观察空间 |
| UNITY_MATRIX_V | 当前的观察矩阵,用于将顶点/方向矢量从世界空间变换到观察空间 |
| UNITY_MATRIX_P | 当前的投影矩阵,用于将顶点/方向矢量从观察空间变换到裁剪空间 |
| UNITY_MATRIX_VP | 当前的观察投影矩阵,用于将顶点/方向矢量从世界空间变换到裁剪空间 |
| UNITY_MATRIX_T_MV | UNITY_MATRIX_MV的转置矩阵 |
| UNITY_MATRIX_IT_MV | UNITY_MATRIX_MV人逆转置矩阵,用于将法线从模型空间变换到观察空间,也可以用于得到UNITY_MATRIX_MV的逆矩阵 |
| _Object2World | 当前的模型矩阵,用于将顶点/方向矢量从模型空间变换到世界空间(依上面规则,这个其实相当于UNITY_MATRIX_M 即模型空间 –> 世界空间) |
| _World2Object | _Object2World的逆矩阵,用于将顶点/方向矢量从世界空间变换到模型空间 |
对照下面这张图,更容易理解一些。
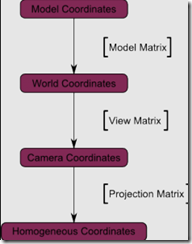
上面这些是基础,只有掌握这些之后,再配置切线、法线、光照模型,在写顶点着色器(Vertex Shader)的时候才不至于懞圈

最后附上常用的矩阵(引用链接:Coding Labs :: World, View and Projection Transformation Matrices)
(1)转换矩阵(Translation Matrix)

(2)绽放矩阵(Scale Matrix)

(3)旋转矩阵(Rotation Matrix) —— 绕 X 轴(around X Axis)

(4)旋转矩阵(Rotation Matrix) —— 绕 X 轴(around Y Axis)
(4)旋转矩阵(Rotation Matrix) —— 绕 Z 轴(around Z Axis)