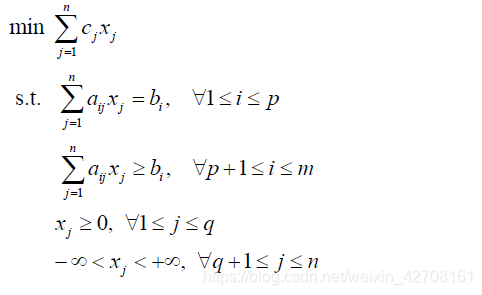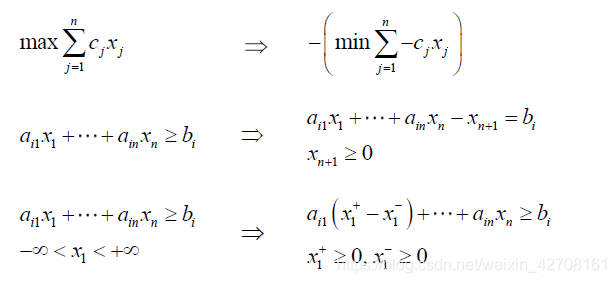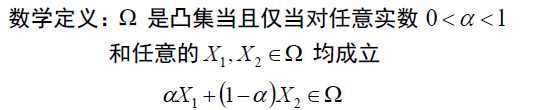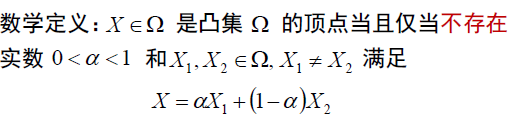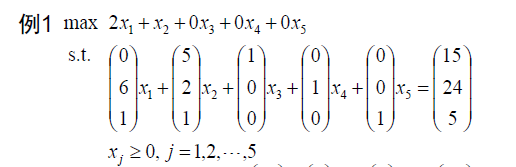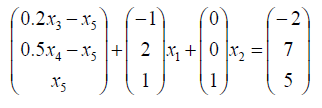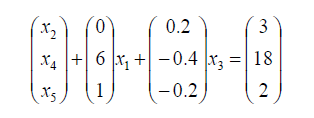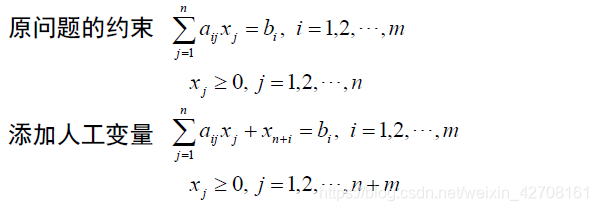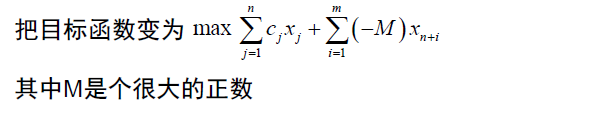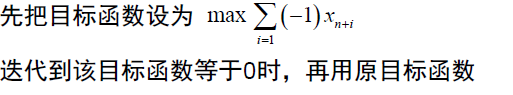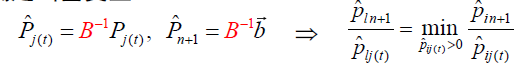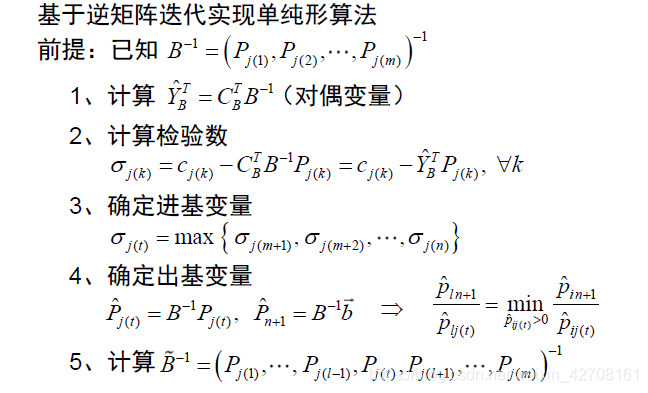线性规划模型

一般模型

一般模型既有不等式约束，也有等式约束；既有非负的约束决策变量，也有整个实数域上的自由决策变量。

标准模型

引入冗余的决策变量，使得不等式约束转化为等式约束。这里的每个决策变量都具有非负性。

把上述模型用矩阵表示就是
$$\begin{gathered} min(ormax)C^{T}X \\ s.tAX=\vec{b} \\ X\ge 0 \end{gathered}$$

线性规划问题的基本假设

1. 系数矩阵A的行向量线性无关。
   如果线性相关有2种可能，要么是增广矩阵的该行也线性相关，则该行约束冗余，可以删去。要么增广矩阵的该行线性无关，则方程无解，优化问题不存在。
2. 系数矩阵A的行数小于列数
   如果行数m大于列数n，则行向量是m个n维向量，不可能线性无关。吐过行数等于列数，且行向量线性无关，则约束条件确定了唯一解，无需优化。

一般模型与标准模型的转化

主要方式是增加决策变量。有两种情况需要增加

1. 不等式变等式，每个不等式增加一个决策变量。
2. 1个自由决策变量转化为2个约束的决策变量。
   

线性规划问题解的可能情况

1. 唯一最优解
2. 没有有限的最优目标函数
3. 没有可行解
4. 无穷多的最优解（一维问题中不会出现）

凸集

Def. 凸集：该集合中任意两个元素的凸组合仍然属于该集合。

注：此处的$\alpha$不能是0或1。
Thm. 线性规划的多面体模型是凸集。
Def. 凸集的顶点：顶点无法表示成集合中其他元素的凸组合。

顶点的等价描述

从系数矩阵中抽取m列线性无关的列向量，组成可逆方阵。则由此可求得m个决策变量的值，再令其余的决策变量为0即可。
推论

1. 顶点中正分量对应的系数向量线性无关。
2. 一个线性规划问题标准模型最多有$C_n^m$个顶点。

定义总结

1. 基矩阵§：系数矩阵中抽取m列线性无关的列向量组成可逆方阵。
2. 基本解：m个基变量有基矩阵和$\vec{b}$决定，剩余(n-m)个变量都置0，称之为非基变量。
3. 基本可行解（顶点）：基本解中可行的，即满足非负性约束
   Thm. 线性规划标准模型的基本可行解就是可行集的顶点。
   Thm. 标准模型的线性规划问题如有可行解，则定有基本可行解。
   Thm. 线性规划标准模型中顶点的个数是有限的。
   Thm. 线性规划标准模型的最优目标函数值如果有有限的目标函数值，则总在顶点处取到。

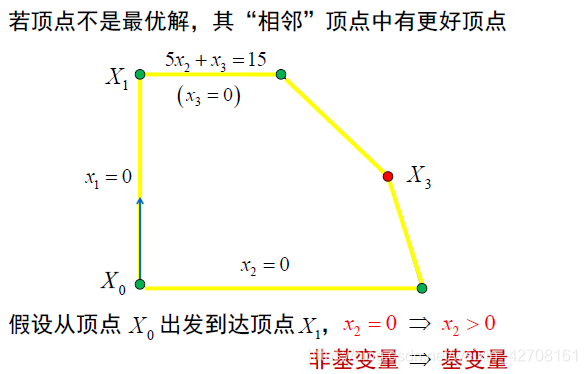
单纯形法

在顶点中沿着边搜索最优解的过程。
按照上述的原理，我们固然可以求出所有的基矩阵，进入求出所有的顶点。计算每一个顶点的目标函数值，找出其中最大的那个，但是这样做的计算量未免太大，因此有了单纯行法，即沿着边搜索顶点。

单纯形法就是一个不断的选择变量入基出基的过程。

1. 假定已知一个基本可行解。（问题4）
2. 如何计算选定进基变量后的基本可行解。(问题1）
3. 如何选择进基变量使得目标函数值改善。（问题2）
4. 如何判断已经找到最优的目标函数值。（问题3）

计算选定进基变量的基本可行解

Def. 基本可行解的表示式：基变量只出现在一个等式约束中。如：

此处的$x_3,x_4,x_5$就是基变量。

选定出基变量：保可行性的最小非负比值原理

由上所述，一个顶点对应一个基本可行解，其中m个基变量，(n-m)个非基变量。假定我们要选择某个非基变量$x_i$入基，实际上就是通过对增广矩阵做初等行变化使得$x_i$仅仅出现在一个等式约束中。比如我们通过变换，使得$x_i$仅仅出现在第j个等式约束中，如果此时仍然满足可行性，那么$x_i$就取代了原来在此处的基变量，成为新的基变量。
在进行初等行变换的过程中，要保证可行性，即$$\vec{b}\ge 0$$
。因此要选择最小非负比值。请看下面的例子：

假设我们要选择$x_2$入基，那么就是要通过初等行变换，使得$x_2$的系数向量中某一行是1，其余行都是0。如我们选择$x_2$仅出现在第3个等式约束中，即

则此时无法保证可行性，因为$\vec{b}$中第1个分量是负数。
为了避免等式右侧出现负数，只能选择比值最小的一行，即第1行。即化成如下的形式：

如果此时我们想让$x_3$入基，此时的最小比值是第2行，即让该行为1，其余行为0。但是，为了让$x_3$的第二行为1，该行两端必须同时乘以一个负数，此时仍然无法保证$\vec{b}\ge 0$，因此只能选择系数非负的一行。
注：这里的非负性是指系数非负，而不是比值非负。即当b中某行分量是0，而该行入基变量系数是负数，仍不能入基。

特殊情况：没有非负比值，即没有有限的目标函数值。

选择入基变量的原则

选择某个入基变量使得目标函数能改善，通过检验数选择。
此处假设优化目标是求最大值。通过等式约束，将目标函数表示成非基变量的线性组合。即
$$f(X)=c_1{x}_{j(m+1)}+c_2{x}_{j(m+2)}+...+c_n{x}_{j(n)}+const$$
只有选择检验数是正数的变量入基才有可能使得目标函数继续增大，因为入基之后变量只可能增大或者不变，而不可能减少。

如何确定已经找到了最优的目标函数值

此处假设优化目标是求最大值。
当每个非基变量的检验数都是负数时，目标函数已经达到了最大值。

退化情况

Thm. 收敛条件：每次迭代过程中，每个基本可行解的基变量都严格大于0，则每次迭代都能保证目标函数严格增加。而基本可行解的数目是有限的，因此上述过程不会一直进行下去，因此一定能在有限次迭代过程中找到最优解。
Def. 退化情况：某些基变量是0。则多个基矩阵对应同一个退化的顶点。
Thm. 循环迭代导致不收敛：多个基矩阵对应一个顶点，即每次出基入基都换了基矩阵，但是对应的退化顶点不变，即目标函数也不变。因此可能出现在几个基矩阵之间循环不止的情况。
避免退化：由于顶点的个数是有限的，我们只需标记那些已经迭代过的顶点，即可避免循环。
**bland法则：**始终选择下标最小的可入基和出基的变量。
当所有的基变量都严格大于0时，则这个基矩阵对应于非退化的顶点，此时可行基矩阵和顶点是一一对应的；
当某些基变量为0时，则这个基矩阵对应退化的顶点，一个退化的顶点对应数个可行基矩阵。
即给定一个可行基矩阵，一定能确定一个顶点，但是给定一个顶点时，其对应的基矩阵可能不唯一。
更一般地说，当顶点非退化时，可行基矩阵唯一；否则可行基矩阵不唯一。

如何确定初始的基本可行解

先将一般模型转化为标准模型，然后添加人工变量，在迭代过程中将人工变量都变成非基变量，则基变量就只剩下原来的变量。

1. 大M法
2. 两阶段法
   

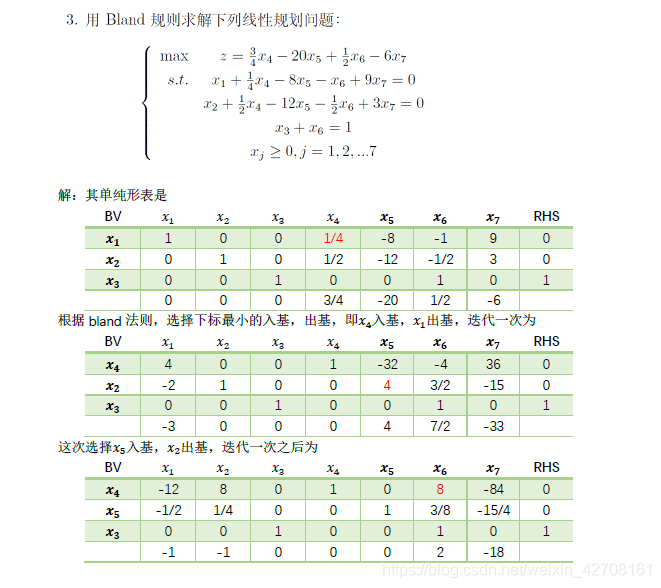
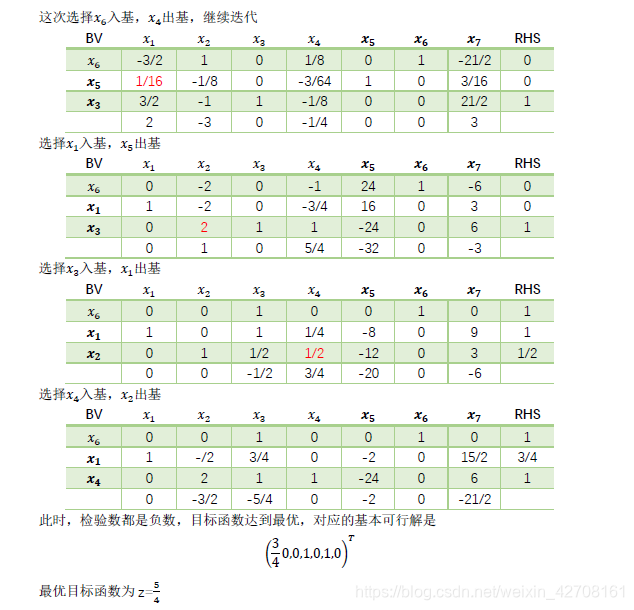
例题

本质就是不断的迭代单纯型表

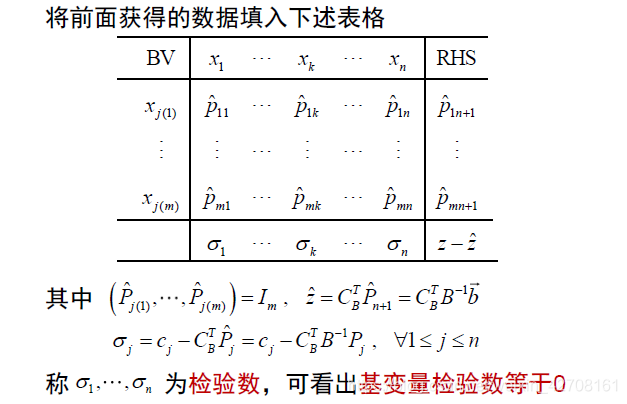
一般线性规划问题总结

1. 一般模型转化为标准型
   
   
   
   
   
   
   
   

基于单纯型表迭代的实质

1. 求出非基变量的检验数
   $${\sigma }_{j(k)}=c_{j(k)}-C_B^T{B}^{-1}{P}_{j(k)}m+1\le k\le n$$
2. 确定进基变量
   σ j ( t ) = m a x { σ j ( m + 1 ) , σ j ( m + 2 ) , . . . σ j ( n ) } \sigma_{j(t)} = max\{\sigma_{j(m+1)},\sigma_{j(m+2)},...\sigma_{j(n)}\} σj(t)​=max{σj(m+1)​,σj(m+2)​,...σj(n)​}
3. 确定出基变量
   
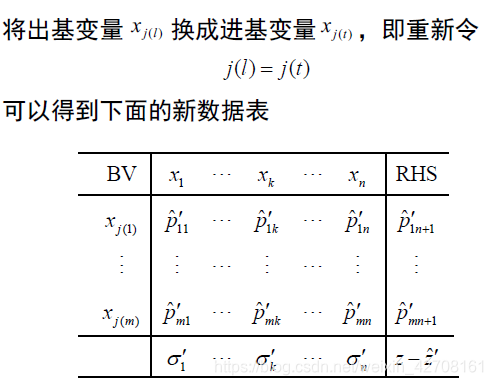
4. 得到新的可行基矩阵
   

基于逆矩阵的单纯形法

核心问题：如何基于$B^{-1}$计算出$\widetilde{B^{-1}}$。这两个矩阵仅仅有1列不一样，这是一个线性代数问题，与本课程的主要内容无关，此处不再赘述。

总结：单纯形法中可能遇到的3中特殊情况。

1. 退化问题：某些基变量为0
退化问题的现象是某些基变量为0，本质是一个退化的顶点对应多个可行基矩阵，后果是可能使得单纯形法不收敛。
在选择入基变量时，应该遵循blend法则，即每次选择可入基变量下标最小的那个。
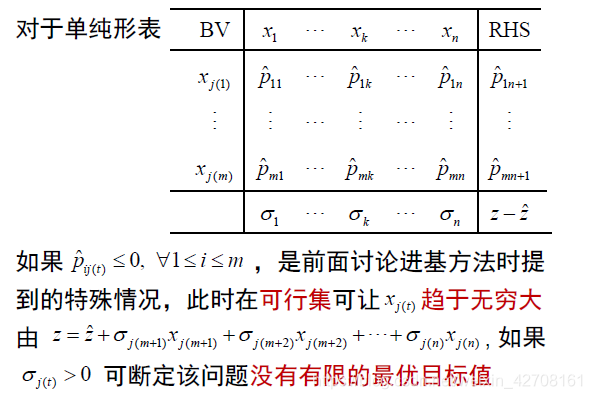
2. 没有最小非负比值。
当选定入基变量后，需要根据“保证可行性的最小非负比值原理”选定出基变量，如果没有非负比值，则说明该变量可以趋于无穷，则该问题没有有限的最优目标函数值。
3. 某个非基变量的检验数为0.
在选择入基变量时，需要将目标函数表示成非基变量的表达式。以目标值是求最大问题的为例，此时应该选择检验数大于0的非基变量入基才能改善目标函数值。
当所有非基变量的检验数都为小于等于0的时候，无论选择谁入基，都会值得目标函数变得更差，因此这时候就达到了最优条件。
有一种特殊情况是某个非基变量的检验数为0，如果选取该变量入基，则目标函数值和原来一样，但是我们得到另一组不同的基本可行解，即最优目标函数值对应了多个基本可行解，这说明原问题有无穷多最优解。
4. 退化问题和非基变量检验数为0.
前者是一个顶点对应多个可行基矩阵，后者是最优目标函数值对应多个顶点。
前者可能导致单纯形法不收敛，后者说明该问题有无穷多解。