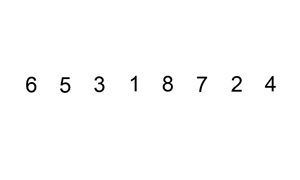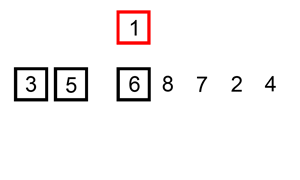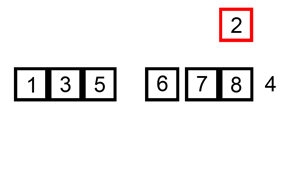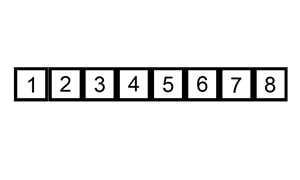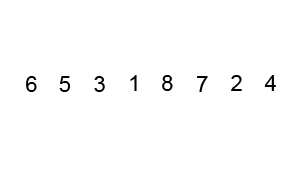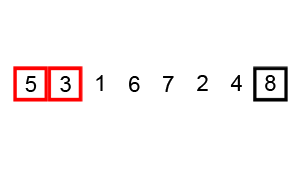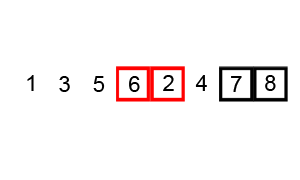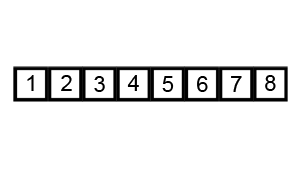第8章 排序
排序是计算机科学中最基本且最常用的操作之一。本章详细介绍了排序算法的概念、分类、每种算法的定义、图示、代码实现及其应用场景。
8.1 基本概念和排序方法概述
8.1.1 排序的基本概念
排序是指将一组无序的记录按照某种指定的顺序重新排列的过程。
排序的目标:
- 按照关键字值重新排列记录。
- 提高后续数据处理(如查找或分析)的效率。
排序分类:
- 内部排序:数据全部加载到内存中进行排序。
- 外部排序:数据量过大,需借助外存完成排序。
8.1.2 内部排序方法的分类
- 插入排序:通过逐步将元素插入已排序部分实现排序,如直接插入排序、折半插入排序、希尔排序。
- 交换排序:通过元素交换实现排序,如冒泡排序、快速排序。
- 选择排序:每次选择最小(或最大)元素放到正确位置,如简单选择排序、堆排序。
- 归并排序:将数据分解成子序列,排序后合并。
- 基数排序:按照关键字的各个位依次进行排序。
8.1.3 待排序记录的存储方式
- 顺序存储:使用数组存储,便于随机访问。
- 链式存储:使用链表存储,适合动态数据插入和删除。
8.1.4 排序算法效率的评价指标
- 时间复杂度:算法运行时间的增长率。
- 空间复杂度:算法占用的额外内存空间。
- 稳定性:排序后值相同的记录是否保持原相对顺序。
- 适应性:算法能否高效处理特定数据分布。
8.2 插入排序
8.2.1 直接插入排序
定义
直接插入排序是一种简单的排序算法,它将当前元素与已排序部分的元素逐一比较,找到正确位置插入。
图示
步骤
- 从第二个元素开始,将其与前面的元素逐一比较。
- 找到插入位置,将当前元素插入。
- 重复以上过程,直到排序完成。
代码实现
def insertion_sort(arr):
for i in range(1, len(arr)):
key = arr[i]
j = i - 1
while j >= 0 and arr[j] > key:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
return arr
# 示例
arr = [5, 3, 4, 1, 2]
print(insertion_sort(arr)) # 输出: [1, 2, 3, 4, 5]
时间复杂度
- 最好情况: O ( n ) O(n) O(n)(已排序)。
- 最坏情况: O ( n 2 ) O(n^2) O(n2)(完全逆序)。
- 平均情况: O ( n 2 ) O(n^2) O(n2)。
8.2.2 折半插入排序
定义
折半插入排序是对直接插入排序的改进,通过二分查找插入位置,减少比较次数。
图示
假设要插入元素 k e y key key:
已排序部分: [1, 3, 5, 7]
插入元素: 4
折半查找后插入: [1, 3, 4, 5, 7]
代码实现
def binary_insertion_sort(arr):
for i in range(1, len(arr)):
key = arr[i]
low, high = 0, i - 1
while low <= high:
mid = (low + high) // 2
if arr[mid] > key:
high = mid - 1
else:
low = mid + 1
for j in range(i, low, -1):
arr[j] = arr[j - 1]
arr[low] = key
return arr
# 示例
arr = [5, 3, 4, 1, 2]
print(binary_insertion_sort(arr)) # 输出: [1, 2, 3, 4, 5]
8.2.3 希尔排序
定义
希尔排序是基于插入排序的改进算法,通过分组对元素排序后逐渐减小组间间隔,最终完成排序。
图示
分组和排序:
原数组:5 3 4 1 2
间隔 = 3: 5 | 1 4 | 2 3
间隔 = 1: 1 2 3 4 5
代码实现
def shell_sort(arr):
n = len(arr)
gap = n // 2
while gap > 0:
for i in range(gap, n):
temp = arr[i]
j = i
while j >= gap and arr[j - gap] > temp:
arr[j] = arr[j - gap]
j -= gap
arr[j] = temp
gap //= 2
return arr
# 示例
arr = [5, 3, 4, 1, 2]
print(shell_sort(arr)) # 输出: [1, 2, 3, 4, 5]
8.3 交换排序
8.3.1 冒泡排序
定义
冒泡排序通过多次遍历数组,每次将当前未排序部分的最大元素移到末尾。
图示
代码实现
def bubble_sort(arr):
n = len(arr)
for i in range(n):
for j in range(0, n - i - 1):
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
return arr
# 示例
arr = [5, 3, 4, 1, 2]
print(bubble_sort(arr)) # 输出: [1, 2, 3, 4, 5]
8.3.2 快速排序
定义
快速排序通过选择一个“基准”元素,将数组分为小于和大于基准的两部分,递归排序。
图示
原数组:5 3 4 1 2
基准:3
左:[1, 2] 基准:[3] 右:[5, 4]
合并:1 2 3 4 5
代码实现
def quick_sort(arr):
if len(arr) <= 1:
return arr
pivot = arr[0]
left = [x for x in arr[1:] if x < pivot]
right = [x for x in arr[1:] if x >= pivot]
return quick_sort(left) + [pivot] + quick_sort(right)
# 示例
arr = [5, 3, 4, 1, 2]
print(quick_sort(arr)) # 输出: [1, 2, 3, 4, 5]
8.4 选择排序
8.4.1 简单选择排序
定义
简单选择排序是一种直接的排序方法,基本思想是:每次从未排序部分中找到最小元素,与未排序部分的第一个元素交换。
图示
假设排序数组 [5, 3, 4, 1, 2]:
- 第1趟:找到最小值 1,交换到第1位。
- 第2趟:找到次小值 2,交换到第2位。
- 重复直到数组排序完成。
最终过程:
原数组: [5, 3, 4, 1, 2]
第一步: [1, 3, 4, 5, 2]
第二步: [1, 2, 4, 5, 3]
第三步: [1, 2, 3, 5, 4]
第四步: [1, 2, 3, 4, 5]
代码实现
def selection_sort(arr):
n = len(arr)
for i in range(n):
# 假设当前最小值的索引
min_index = i
for j in range(i + 1, n):
if arr[j] < arr[min_index]:
min_index = j
# 交换最小值与当前值
arr[i], arr[min_index] = arr[min_index], arr[i]
return arr
# 示例
arr = [5, 3, 4, 1, 2]
print(selection_sort(arr)) # 输出: [1, 2, 3, 4, 5]
时间复杂度
- 最好、最坏、平均情况: O ( n 2 ) O(n^2) O(n2)。
- 特点:简单实现,但效率较低。
8.4.2 树形选择排序
定义
树形选择排序使用树形结构(胜者树)来选出最小元素并进行排序,适用于大规模数据。
思路:
- 构造一棵胜者树,其中每个非叶子节点存储两子节点中较小的值。
- 通过调整树结构,快速找到次小值。
8.4.3 堆排序
定义
堆排序是一种利用堆这种特殊树形结构的选择排序算法。堆是一棵完全二叉树,其中每个节点的值都大于(或小于)其子节点的值。
图示
- 构造初始堆:
原数组: [5, 3, 4, 1, 2]
初始大顶堆: [5, 3, 4, 1, 2]
- 取出堆顶元素(最大值),与最后一个元素交换。
- 调整剩余元素形成新的大顶堆。
代码实现
def heapify(arr, n, i):
largest = i # 初始化最大值为根节点
left = 2 * i + 1 # 左子节点
right = 2 * i + 2 # 右子节点
# 检查左子节点
if left < n and arr[left] > arr[largest]:
largest = left
# 检查右子节点
if right < n and arr[right] > arr[largest]:
largest = right
# 如果最大值不是根节点,交换并递归调整
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i]
heapify(arr, n, largest)
def heap_sort(arr):
n = len(arr)
# 构造大顶堆
for i in range(n // 2 - 1, -1, -1):
heapify(arr, n, i)
# 逐步取出堆顶元素
for i in range(n - 1, 0, -1):
arr[i], arr[0] = arr[0], arr[i]
heapify(arr, i, 0)
return arr
# 示例
arr = [5, 3, 4, 1, 2]
print(heap_sort(arr)) # 输出: [1, 2, 3, 4, 5]
时间复杂度
- 构造堆: O ( n ) O(n) O(n)。
- 排序: O ( n log n ) O(n \log n) O(nlogn)。
8.5 归并排序
8.5.1 定义
归并排序是一种基于分治思想的排序算法,将数组递归分割为多个子序列,分别排序后再合并。
8.5.2 图示
原数组: [5, 3, 4, 1, 2]
分割: [5, 3, 4] 和 [1, 2]
分割: [5], [3, 4], [1], [2]
合并: [3, 4], [1, 2]
合并: [1, 2, 3, 4, 5]
8.5.3 代码实现
def merge_sort(arr):
if len(arr) <= 1:
return arr
mid = len(arr) // 2
left = merge_sort(arr[:mid])
right = merge_sort(arr[mid:])
return merge(left, right)
def merge(left, right):
result = []
i = j = 0
while i < len(left) and j < len(right):
if left[i] < right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result.extend(left[i:])
result.extend(right[j:])
return result
# 示例
arr = [5, 3, 4, 1, 2]
print(merge_sort(arr)) # 输出: [1, 2, 3, 4, 5]
8.5.4 时间复杂度
- 分割: O ( log n ) O(\log n) O(logn)。
- 合并: O ( n ) O(n) O(n)。
- 总复杂度: O ( n log n ) O(n \log n) O(nlogn)。
8.6 基数排序
8.6.1 定义
基数排序是一种非比较排序算法,将数据根据关键字的个位、十位、百位等进行多轮排序。
8.6.2 图示
排序数组 [329, 457, 657, 839, 436, 720, 355]:
- 按个位排序:[720, 355, 436, 657, 457, 329, 839]
- 按十位排序:[329, 720, 436, 839, 355, 457, 657]
- 按百位排序:[329, 355, 436, 457, 657, 720, 839]
8.6.3 代码实现
def radix_sort(arr):
max_num = max(arr)
exp = 1 # 从个位开始
while max_num // exp > 0:
counting_sort(arr, exp)
exp *= 10
def counting_sort(arr, exp):
n = len(arr)
output = [0] * n
count = [0] * 10
# 统计计数
for i in range(n):
index = (arr[i] // exp) % 10
count[index] += 1
# 累计计数
for i in range(1, 10):
count[i] += count[i - 1]
# 排序输出
for i in range(n - 1, -1, -1):
index = (arr[i] // exp) % 10
output[count[index] - 1] = arr[i]
count[index] -= 1
for i in range(n):
arr[i] = output[i]
# 示例
arr = [329, 457, 657, 839, 436, 720, 355]
radix_sort(arr)
print(arr) # 输出: [329, 355, 436, 457, 657, 720, 839]
8.7 外部排序
8.7.1 外部排序的定义与基本概念
定义
外部排序是指数据量远大于内存容量时,通过将数据分块处理的方式,在内存和外存之间协调完成的排序方法。其基本思想是:
- 将数据划分为若干个适合内存大小的块,在内存中分别排序后存储到外存。
- 通过多路归并算法,将各已排序块合并为一个有序文件。
特点
- 适用场景:大规模数据排序(数据无法一次性装入内存)。
- 核心操作:分块排序 + 归并。
- 关键问题:提高内存与外存之间的数据交换效率。
8.7.2 外部排序的基本方法
外部排序主要包含以下核心步骤:
- 分块排序:将数据划分成多个“适合内存大小的子文件”,每个子文件在内存中排序后存入外存。
- 归并排序:使用多路归并算法将子文件合并为一个整体。
8.7.3 核心算法
1. 多路平衡归并
定义
多路平衡归并是一种在外存排序过程中常用的合并技术,利用多个缓冲区同时读取多个已排序块,通过逐步合并最终生成一个有序结果。
算法步骤
- 从外存中选取 k k k 个已排序块(假设总共分为 k k k 块)。
- 为每个块设置一个输入缓冲区,每次从缓冲区中读取当前块的最小值。
- 将最小值写入输出缓冲区;当缓冲区为空时从对应的块中继续读取。
- 重复上述过程直到所有块归并完成。
图示
假设有 4 个已排序块,内容如下:
块1: [2, 6, 9]
块2: [1, 5, 7]
块3: [3, 4, 8]
块4: [0, 10, 11]
归并过程:
- 初始化:从每个块中读取首元素,选最小值 0 0 0(块4)。
- 移动块4指针,写入输出缓冲区并继续归并。
- 逐步归并得到最终排序结果:
输出结果: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
代码实现
import heapq
def multiway_merge(sorted_blocks):
"""
多路平衡归并实现
:param sorted_blocks: 已排序的子块(列表列表)
:return: 归并后的结果
"""
heap = []
result = []
# 初始化最小堆,存储 (值, 块索引)
for i, block in enumerate(sorted_blocks):
if block:
heapq.heappush(heap, (block[0], i, 0)) # (值, 块索引, 块内元素索引)
# 归并过程
while heap:
val, block_index, element_index = heapq.heappop(heap)
result.append(val) # 将最小值加入结果
# 如果块中还有数据,将下一元素压入堆
if element_index + 1 < len(sorted_blocks[block_index]):
next_val = sorted_blocks[block_index][element_index + 1]
heapq.heappush(heap, (next_val, block_index, element_index + 1))
return result
# 示例
sorted_blocks = [
[2, 6, 9],
[1, 5, 7],
[3, 4, 8],
[0, 10, 11]
]
print(multiway_merge(sorted_blocks))
# 输出: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
2. 置换-选择排序
定义
置换-选择排序是一种用于生成初始分块的算法,其通过维护一个最小堆实现。它能够在生成块的同时尽可能延长块的长度,从而减少后续归并的块数。
算法步骤
- 将内存缓冲区填满,形成一个最小堆。
- 从堆中取出最小值,写入当前块。
- 将下一个数据项插入堆中(若大于堆顶),否则写入下一个块。
- 继续上述过程直到所有数据处理完。
图示
假设排序输入:[5, 1, 7, 3, 9, 2],缓冲区大小为3:
- 初始化堆:[1, 5, 7]。
- 取出最小值 1 1 1,加入当前块。
- 插入新元素 3 3 3,堆调整为:[3, 5, 7]。
- 重复,最终分为块:[1, 3, 5], [7, 9, 2]。
代码实现
import heapq
def replacement_selection_sort(data, buffer_size):
"""
置换-选择排序生成初始分块
:param data: 输入数据
:param buffer_size: 缓冲区大小
:return: 分块列表
"""
blocks = []
buffer = []
block = []
# 初始化缓冲区
for i in range(min(buffer_size, len(data))):
heapq.heappush(buffer, data.pop(0))
while buffer:
# 将堆顶元素写入当前块
smallest = heapq.heappop(buffer)
block.append(smallest)
if data:
next_element = data.pop(0)
if next_element >= smallest:
heapq.heappush(buffer, next_element)
else:
# 启动新块
blocks.append(block)
block = [next_element]
# 当堆为空时将最后一块加入结果
if not buffer and block:
blocks.append(block)
return blocks
# 示例
data = [5, 1, 7, 3, 9, 2]
buffer_size = 3
print(replacement_selection_sort(data, buffer_size))
# 输出: [[1, 3, 5], [7, 9, 2]]
3. 最佳归并树
定义
最佳归并树是一种优化归并过程的技术,目标是通过构造一棵最优二叉树,尽可能减少归并次数或读取外存次数。
特点
- 优化目标:尽量使所有子块的读取均匀分布。
- 应用场景:多路归并时提高效率。
算法步骤
- 根据子块的大小构造一棵哈夫曼树。
- 将每个块作为叶子节点,根据权值(块大小)构造最优树。
- 按树结构顺序读取数据进行归并。
8.7.4 总结
外部排序是一种解决大规模数据排序问题的关键技术,其核心是 分块排序 和 归并排序 的结合。
- 多路平衡归并:通过多路堆优化归并效率。
- 置换-选择排序:延长初始块长度,减少归并次数。
- 最佳归并树:在多路归并中减少外存读取次数。
外部排序的应用广泛,如数据库排序、日志分析等,其算法实现兼顾了时间复杂度和内存使用效率。