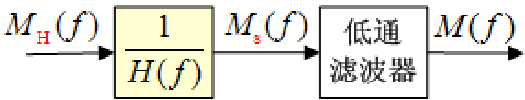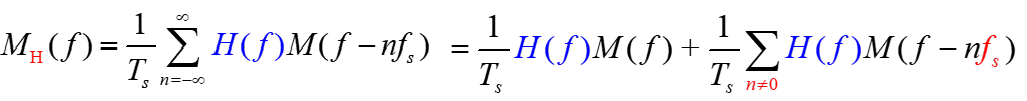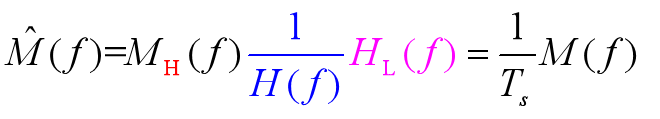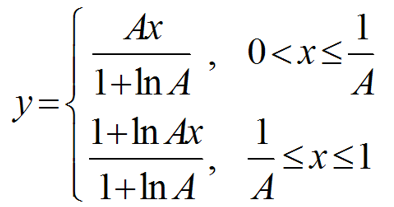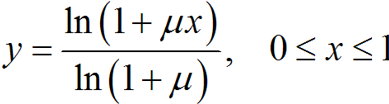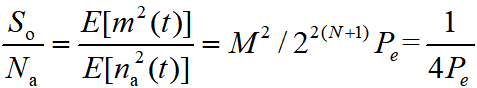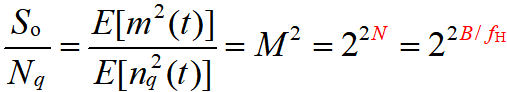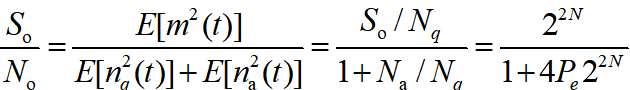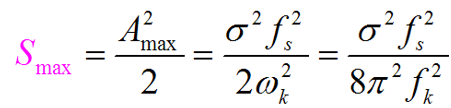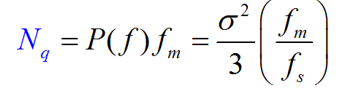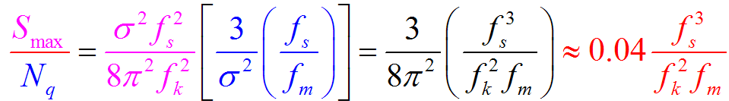写在前面:本博客是《通信原理》的学习笔记,仅供个人学习记录使用
一、一些定义
(1)信源编码:将数字或模拟信号编码为更紧凑形式的过程。
(2)目的:通过消除冗余信息和利用信号自身的统计特性,使得信号能够以更高效的方式表示和传输。它可以帮助减少存储或传输所需的比特数,从而达到节省带宽或存储空间的效果。
(3)模拟信号数字化传输的三个环节:抽样(Sampling)、量化(Quantization)、编码(Coding)。
- 抽样:将模拟信号时间离散化; 量化:将抽样信号幅度离散化;编码:将量化信号二进制化
二、模拟信号的抽样
1. 抽样定理
(1)低通模拟信号的抽样定理
- 定理:设一个连续模拟信号 m ( t ) m(t) m(t)的最高频率 < f H <f_{H} <fH,则以间隔时间为 T s ≤ 1 / 2 f H T_{s}\le 1/2f_{H} Ts≤1/2fH的周期性脉冲对它抽样时, m ( t ) m(t) m(t)将被这些抽样值所完全确定。
- 奈奎斯特间隔:最高 T s = 1 / 2 f H T_{s}=1/2f_{H} Ts=1/2fH
- 奈奎斯特速率:最低 f s = 2 f H f_{s}=2f_{H} fs=2fH
- 如果抽样速率不满足
T
s
≤
1
/
2
f
H
T_{s}\le 1/2f_{H}
Ts≤1/2fH,信号将产生
混叠失真
(2)带通模拟信号的抽样定理
- 定理:设带通模拟信号 m ( t ) m(t) m(t)的频率限制在 f L f_{L} fL和 f H f_{H} fH之间,信号带宽为 B = f H − f L B=f_{H}-f_{L} B=fH−fL,则此带通模拟信号的抽样频率范围为 2 f H N ≤ f s ≤ 2 f L N − 1 \frac{2f_{H}}{N} \le f_{s}\le \frac{2f_{L}}{N-1} N2fH≤fs≤N−12fL。 其中, N N N为商 f H / B f_{H}/B fH/B的整数部分。 f L = 0 f_{L}=0 fL=0时, f s = 2 B = 2 f H f_{s}=2B=2f_{H} fs=2B=2fH,为低通抽样情况
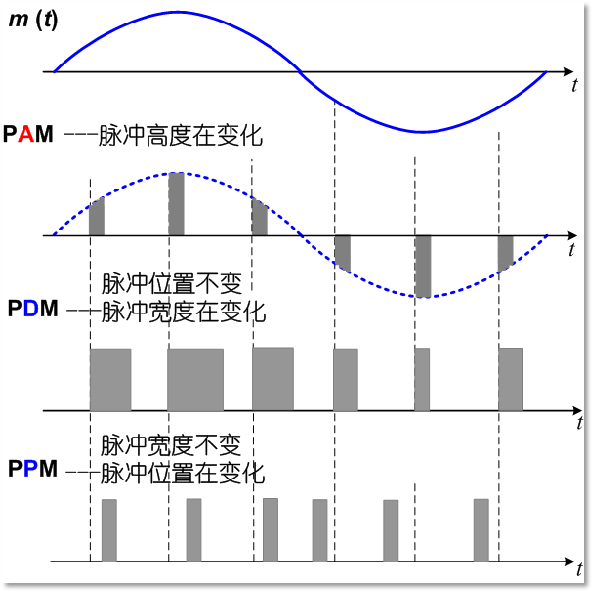
2. 模拟脉冲调制信号的抽样
- PAM:脉冲振幅调制;PDM:脉冲宽度调制;PPM:脉冲位置调制
(1)自然抽样
- 又称曲顶抽样,它是指抽样后信号的脉冲顶部与原模拟信号的波形相同。
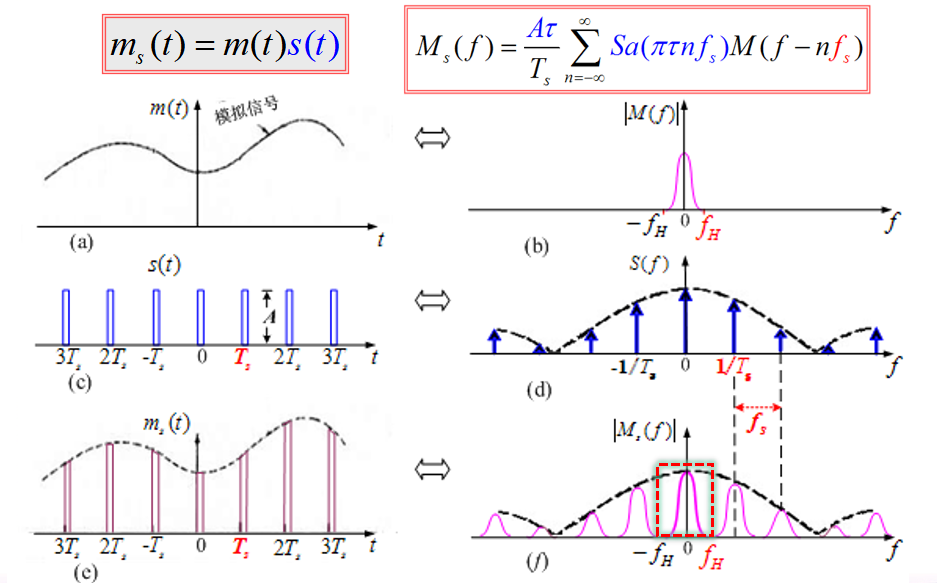
- PAM自然抽样过程的波形和频谱如下:
- 恢复:可用理想低通滤波器取出原信号。
(2)平顶抽样
- 平顶抽样,即抽样后的矩形脉冲顶部形状是平坦的。
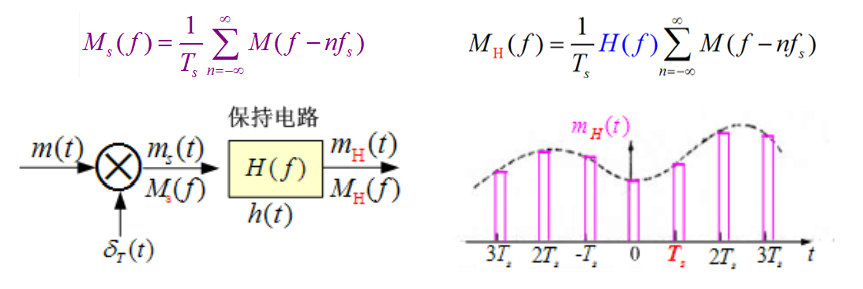
- PAM平顶抽样的产生过程及波形图如下:
平顶抽样的信号频谱被脉冲形成电路的频谱 H ( f ) H(f) H(f)加权,产生频率失真,也叫做孔径失真。 - 恢复:修正+低通滤波
三、模拟信号的量化
1. 均匀量化
(1)均匀量化:等间隔划分输入信号的取值域
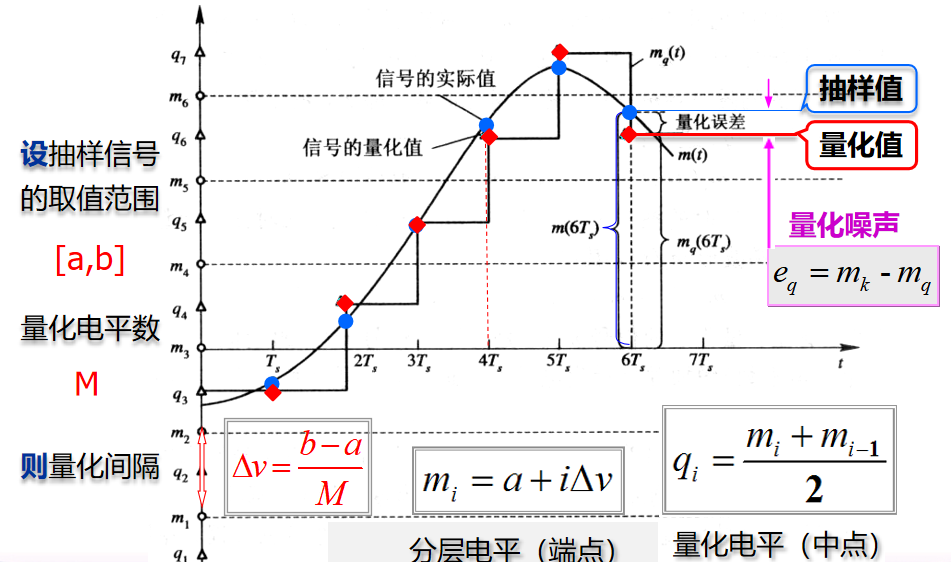
- 均匀量化示意图:
假如 m k m_{k} mk为模拟信号的抽样值,即 m ( k T ) m(kT) m(kT); m q m_{q} mq为量化信号值,即 m q ( k T ) m_{q}(kT) mq(kT); f ( m k ) f(m_{k}) f(mk)为信号抽样值 m k m_{k} mk的概率密度; E E E表示求统计平均值; M M M为量化电平数; Δ V = ( b − a ) / M \Delta V=(b-a)/M ΔV=(b−a)/M是均匀量化间隔; M M M电平为 N N N为编码有 M = 2 N M=2^{N} M=2N。 - 量化误差: e q = m k − m q e_{q}=m_{k}-m_{q} eq=mk−mq,在量化区, ∣ e q ∣ ≤ Δ 2 |e_{q}|\le \frac{\Delta }{2} ∣eq∣≤2Δ,过载区 ∣ e q ∣ > Δ 2 |e_{q}|> \frac{\Delta }{2} ∣eq∣>2Δ
- 量化噪声: N q = ( Δ V ) 2 12 N_{q}=\frac {(\Delta V)^{2}}{12} Nq=12(ΔV)2
- 平均信号量噪比: S N q = M 2 \frac {S}{N_{q}}=M^{2} NqS=M2 或 ( S N q ) d B = 20 l g M = 20 N l g 2 ≈ 6 N ( d B ) (\frac {S}{N_{q}})_{dB}=20lgM=20Nlg2\approx 6N(dB) (NqS)dB=20lgM=20Nlg2≈6N(dB)
(2)正弦信号的均匀量化
- 量噪比:
S
N
R
d
B
≈
4.77
+
20
l
g
D
+
6.02
n
SNR_{dB}\approx 4.77+20lgD+6.02n
SNRdB≈4.77+20lgD+6.02n
这里 n n n为量化编码位数; D = A m / 2 M D=A_{m}/\sqrt{2} M D=Am/2M为正弦信号的归一化有效值。
满载时,信号功率达到最大,最大量化信噪比为 S N R d B , m a x ≈ 1.76 + 6.02 n SNR_{dB,max}\approx 1.76+6.02n SNRdB,max≈1.76+6.02n
(3)均匀量化的缺点
- 由于量化间隔固定,量化噪声固定,会使得小信号的量化信噪比降低,从而限制了输入信号的动态范围(满足信噪比要求的输入信号的取值范围)。
- 电话传输标准要求在信号动态范围为 40 ~ 50 d B 40~50dB 40~50dB的条件下,信号量噪比 S / N q ≥ 26 d B S/Nq≥26dB S/Nq≥26dB。此时需要的编码位数多(11~12位),导致编码信号的带宽增大,且编码设备复杂。
(4)均匀量化的应用:主要用于概率密度为均匀分布的信号,如遥测遥控信号、图像信号数字化接口中。
2. 非均匀量化
- 原因:为了解决均匀量化带来的小信号量化信噪比恶化问题。
- 设计思想:信号样值小, Δ V \Delta V ΔV也小;信号样值大, Δ V \Delta V ΔV也大,即‘压大补小’的非线性变换。
- 实现方法:
压缩使小样值被抬高,大样值被压小,但程度较轻。
(1) A A A压缩律——13折线近似法
- 中国大陆、欧洲各国及国际间互连时采用 A A A律
-
A
A
A律是指满足下式的对数压缩规律:
- A = 1 A=1 A=1时无压缩效果;在实际应用中, A = 87.6 A=87.6 A=87.6
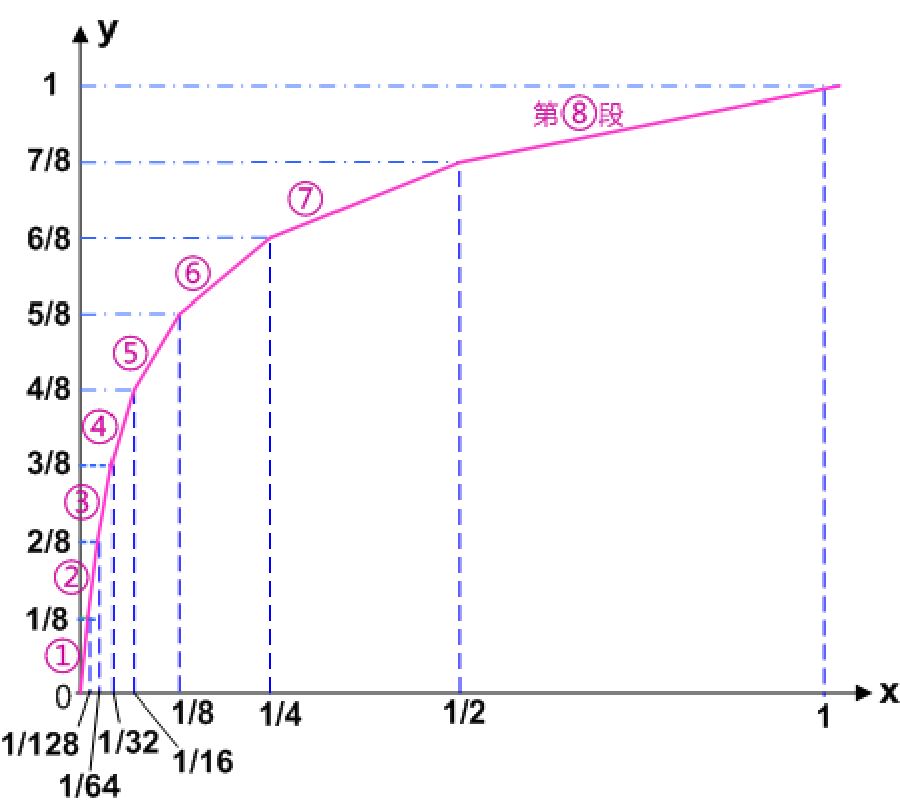
- 13折线特性为:
由上图可知,纵坐标 y y y均匀的划分成8段,横坐标 x x x在0到1的区间内分成不均匀的8段。各段折线的斜率为:
(2) μ \mu μ压缩律——15折线近似法
-
北美、日本和韩国等少数国家和地区采用 μ \mu μ律。
-
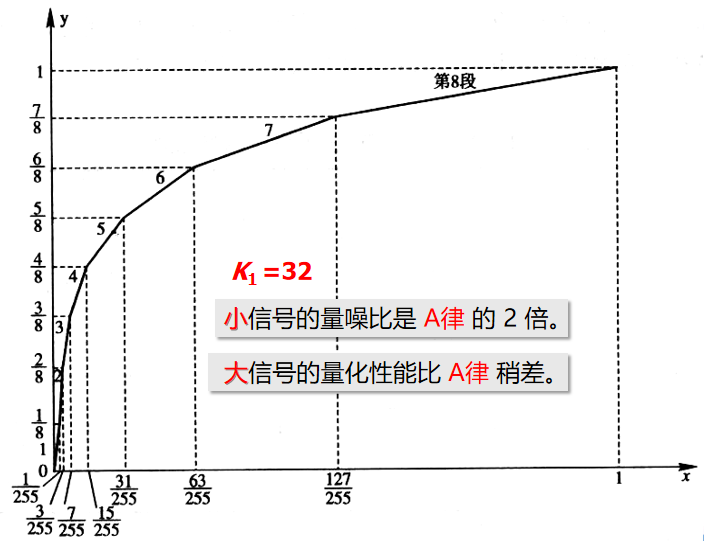
μ \mu μ律为:
-
μ = 0 \mu =0 μ=0时无压缩效果,常用 μ = 255 \mu =255 μ=255
-
15折线特性为:
四、脉冲编码调制(PCM)
1. PCM系统原理框图
2. 折叠码
- 最常用的编码结构为:折叠二进制码
- 在A律13折线 PCM编码中,共计 2 × 8 × 16 = 256 = 2 8 2\times 8\times 16=256=2^{8} 2×8×16=256=28个量化级
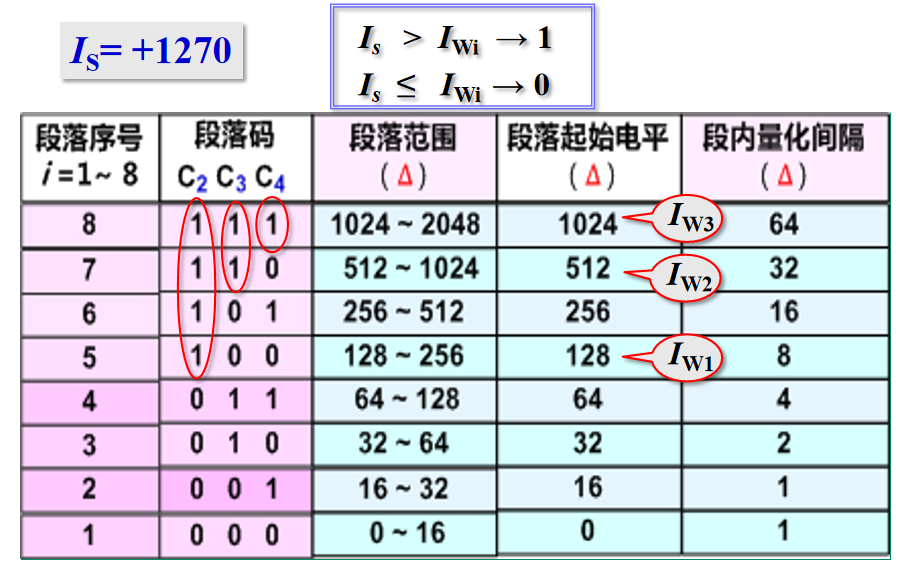
- 编码方式:逐次比较型
(1)需将每个样值脉冲
I
s
Is
Is编成 8位二进制码:
- 极性码:表示样值的极性。正编“1”,负编“0”
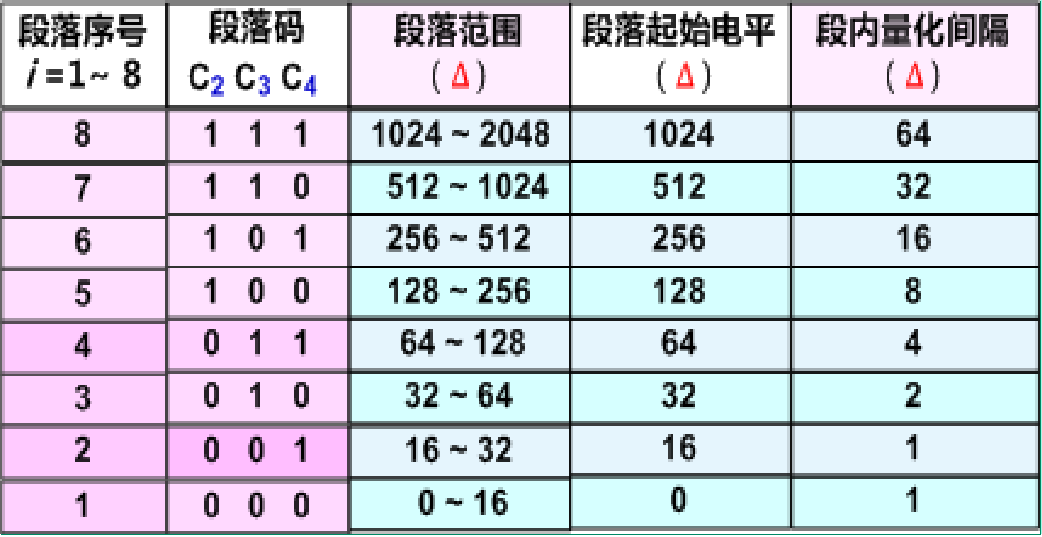
- 段落码:表示样值的幅度所处的段落,即每一段的起始电平
- 段内码:16种可能状态对应代表各段内的16个量化级,即段内均匀量化区间的起始电平
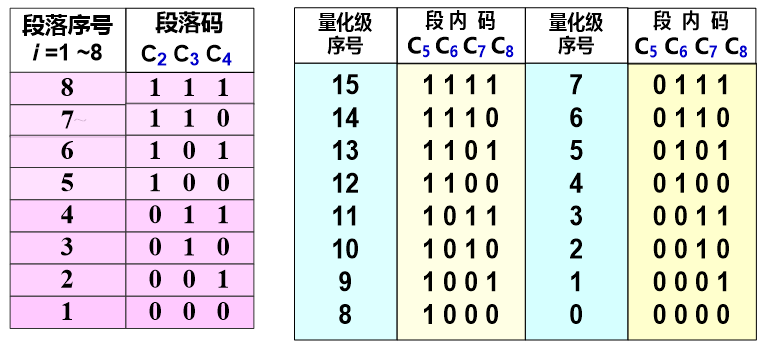
(2)段落码和段内码的编码规则:
(3)起始电平和量化间隔:
- 归一化输入电压的最小量化单位: Δ = 1 2048 \Delta = \frac{1}{2048} Δ=20481
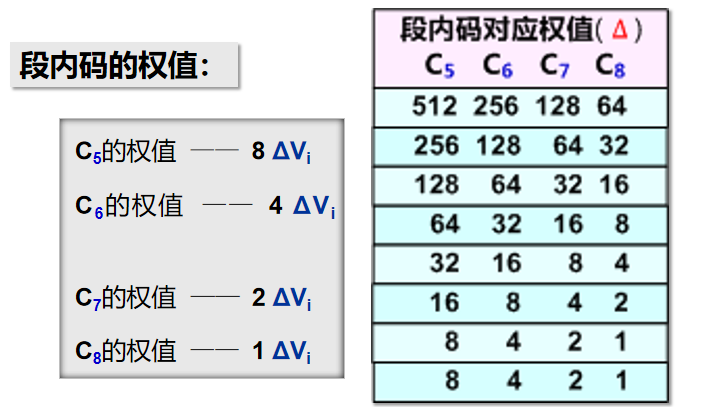
(4)段内码对应权值:
3. 非线性码与线性码(7/11)
(1)编码
- 非线性码对应非均匀量化:只需要7位(非线性)编码,又名非线性/对数PCM编码, M = 8 × 16 = 128 = 2 7 M=8\times 16=128=2^{7} M=8×16=128=27
- 线性码对应均匀量化:以 Δ \Delta Δ对13折线正极性的8个段落进行均匀量化,则量化级数, M = 2048 = 2 11 M=2048=2^{11} M=2048=211,需要11位(线性)编码,又名线性PCM编码
举个栗子:
(2)译码
- 在译码时,将7位非线性码转变为12位线性码(7/12变换电路),目的是增加一个 Δ V i / 2 \Delta V_{i}/2 ΔVi/2恒流电流,人为地补上半个量化级,使最大量化误差不超过 Δ V i / 2 \Delta V_{i}/2 ΔVi/2 , 从而改善量化信噪比。
- 在译码时,译码电平为为
两段的中间数
举个栗子:
4. PCM信号的比特率和带宽
- 设模拟信号的最高频率为 f H f_{H} fH,抽样速率 f s = 2 f H f_{s}=2f_{H} fs=2fH,二进制编码位数为 N N N,则PCM信号的比特率为: R b = f s N = 2 f H N R_{b}=f_{s}N=2f_{H}N Rb=fsN=2fHN
- 传输带宽:若采用非归零矩形脉冲传输时,谱零点带宽为: B = R B = R b = f s N B=R_{B}=R_{b}=f_{s}N B=RB=Rb=fsN
5. PCM系统中噪声的影响
假设条件:自然码、均匀量化、输入信号为均匀分布
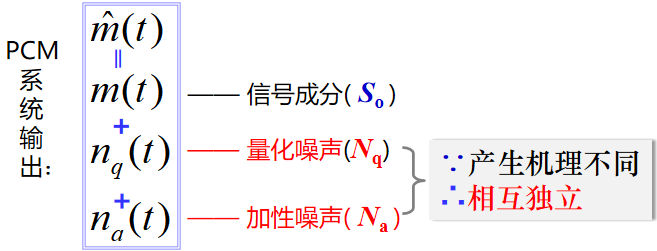
- 两种噪声:
- 性能指标:
抗加性噪声性能:
抗量化噪声性能:
含义:当低通信号最高频率 f H f_{H} fH给定时, PCM系统的输出信号量噪比随系统的带宽 B B B按指数规律增长。——带宽与信噪比互换
总输出信噪比:
这里有: S o N o ≈ { 2 2 N 若 N a ≪ N q 1 4 P e 若 N a ≫ N q \frac{S_{o}}{N_{o}}\approx \begin{cases} 2^{2N} & \text{若} N_{a}\ll N_{q}\\ \frac{1}{4P_{e}} & \text{若} N_{a}\gg N_{q}\end{cases} NoSo≈{22N4Pe1若Na≪Nq若Na≫Nq
6. PCM30/32时分多路复用通信系统
P C M 30 / 32 PCM30/32 PCM30/32路制式基群帧,共由32路组成,其中30路用来传输用户话语,2路用作控制与信令。
(1)抽样周期:抽样时,各路每轮一次的总时间
- 每路话音信号抽样速率 f s = 8000 H z fs=8000Hz fs=8000Hz,每帧时间间隔为 T s = 1 / f s = 125 μ s T_{s}=1/f_{s}=125μs Ts=1/fs=125μs
(2)帧长度:一帧包含多少个信息比特
- 一帧共有 n = 32 n=32 n=32个时间间隔,称为时隙。
- 每个时隙传输一个PCM码组,为 m = 8 b i t m=8bit m=8bit,一帧共包含 256 256 256个比特。
(3)路时隙:在合路的PAM信号中,每个样值所允许占的时间间隔
- T c = T s / n = 125 / 32 = 3.91 u s T_{c}=T_{s}/n=125/32=3.91us Tc=Ts/n=125/32=3.91us
(4)位时隙:一位码所占用的时间
- T b = T c / m = 3.91 / 8 = 0488 u s T_{b}=T_{c}/m=3.91/8=0488us Tb=Tc/m=3.91/8=0488us
(5)信息传输速率:每秒可以传输的平均信息量/比特数
- 总传输速率: R b = 1 / T b = m × n × f s = 8 × 32 × 8000 = 2048 K b i t / s R_{b}=1/T{b}=m\times n\times f_{s}=8\times 32\times 8000=2048Kbit/s Rb=1/Tb=m×n×fs=8×32×8000=2048Kbit/s
- 一路传输速率: R b 1 = R b / n = 64 K b i t / s R_{b}^{1}=R_{b}/n=64Kbit/s Rb1=Rb/n=64Kbit/s
(6)PCM30/32集群编码
- PCM一次群,二次群,三次群均为HDB3码
- PCM四次群为CMI码
五、增量调制
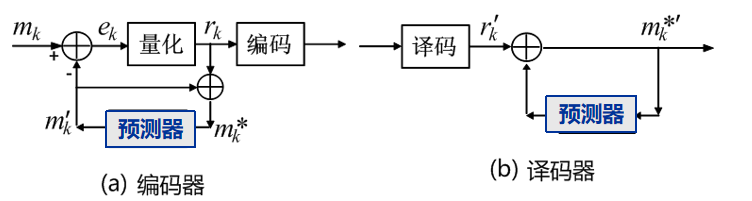
1. 差分脉冲编码调制(DPCM)
- DPCM提出的目的:利用相邻抽样值之间的相关性,减少信息冗余,获得压缩效果。DPCM是PCM的改进型,是一种预测编码方法。
- DPCM方法:对相邻样值的差值进行编码
- DPCM的信号量噪比:
- 显然,若要求DPCM与PCM具有相同的信噪比,则可减少量化器的量化级数,即编码位数减少,比特率降低,带宽减小。
2. 增量调制( Δ M \Delta M ΔM)
(1)增量调制是一种最简单的 DPCM,当DPCM系统中量化电平数取2时,DPCM系统便成为 Δ M \Delta M ΔM系统。
- PCM用 N N N位码表示一个抽样值,反映样值本身的大小; Δ M \Delta M ΔM用1位码表示一个抽样值,反映相邻样值相对大小的变化。
- 与PCM相比, Δ M \Delta M ΔM编译码简单,低比特率时的量化信噪比高,抗误码特性好等优点,广泛用在军事和工业部门的专用通信网和卫星通信中。
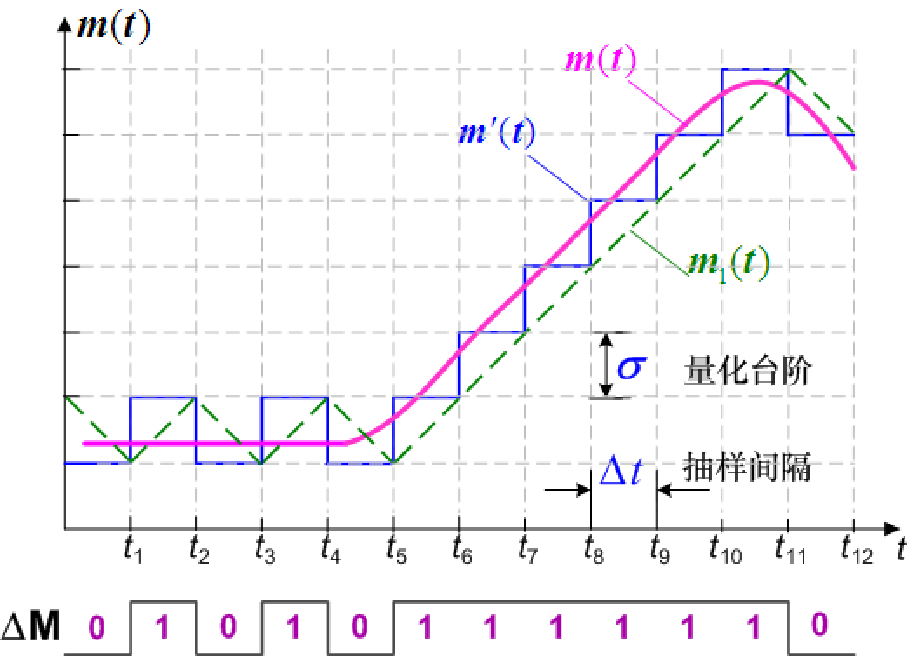
- 增量调制波形图:
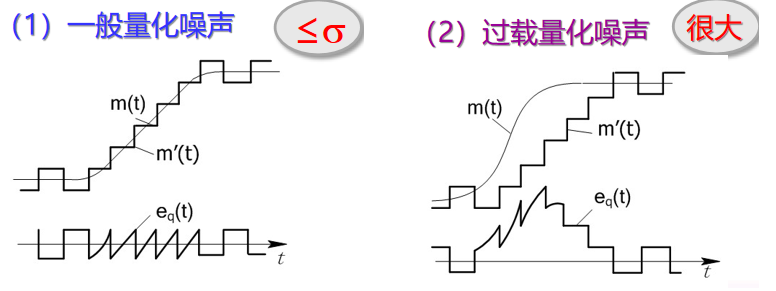
(2)增量调制系统中的量化噪声
- 如果输入信号: m ( t ) = A s i n w k t m(t)=Asinw_{k}t m(t)=Asinwkt,则其斜率为: d m ( t ) d t = A w k c o s w k t \frac{dm(t)}{dt}=Aw_{k}cosw_{k}t dtdm(t)=Awkcoswkt
- 设抽样周期为 T s T_{s} Ts,抽样频率为 f s = 1 / T s f_{s}=1/T_{s} fs=1/Ts,量化台阶为 σ \sigma σ,则一个阶梯台阶的斜率为 k = σ / T s = σ f s k=\sigma /T_{s}=\sigma f_{s} k=σ/Ts=σfs
由此可知为了不发生过载,要求信号的最大斜率不超过译码器的最大跟踪斜率。即:
A
w
k
≤
σ
T
=
σ
⋅
f
s
⟹
A
m
a
x
=
σ
⋅
f
s
w
k
Aw_{k}\le \frac{\sigma }{T}=\sigma \cdot f_{s} \Longrightarrow A_{max}=\frac{\sigma \cdot f_{s}}{w_{k}}
Awk≤Tσ=σ⋅fs⟹Amax=wkσ⋅fs
为了避免过载和增大编码范围,应合理选择 σ \sigma σ和 f s f_{s} fs !
-
σ
\sigma
σ选大 : 有利于减小过载噪声 ,但一般量化噪声增大。
——原因:简单 Δ M ΔM ΔM 的量化台阶是固定的,难以使两者都不超过要求。
——解决:采用自适应 Δ M ΔM ΔM,使量化台阶随信号的变化而变化。 - f s f_{s} fs 选大:对减小过载噪声和一般量化噪声都有利。因此,对于语音信号而言, Δ M ΔM ΔM的抽样频率在几十千赫 ~ 百余千赫。
(3)编码范围: A m i n ∼ A m a x A_{min}\sim A_{max} Amin∼Amax
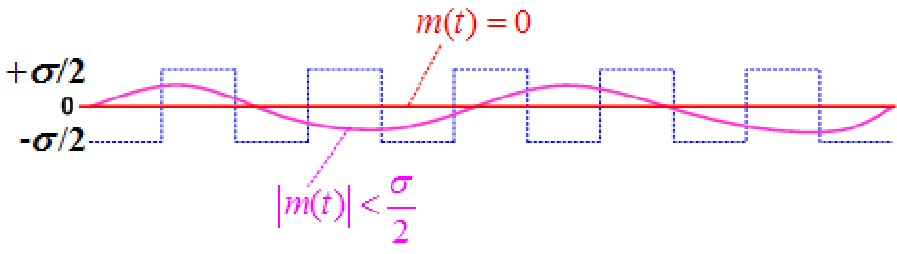
- 起始编码电平: A m i n = σ / 2 A_{min}=\sigma /2 Amin=σ/2
- 含义:当信号的峰值电压
>
σ
/
2
>σ/2
>σ/2时,才能正常编码。这时,输出序列才能反映信号的变化情况。
- 最大编码电平: A m a x = σ ⋅ f s w k = σ ⋅ f s 2 π f k A_{max}=\frac{\sigma \cdot f_{s}}{w_{k}}=\frac{\sigma \cdot f_{s}}{2\pi f_{k}} Amax=wkσ⋅fs=2πfkσ⋅fs
- 可见,当跟踪斜率一定时,允许的信号幅度随信号频率 w k w_{k} wk的增加而减小,这将导致语音高频段的信号量噪比下降。
(4)信号量噪比
- 信号最大功率:
- 量化噪声:
- 最大信号量噪比:在正弦输入信号临界振幅条件下