前言
奇异谱分析(SSA)是主成分分析(PCA)的一个特例,它特别适用于分析一维时间序列,能有效的提取时间序列中的趋势项、周期项、半周期项等有用信号,也可以实现数据的去噪、插值和外推等,是应用极为广泛的一种时间序列分析方法。这里对SSA算法的理解和实现过程进行总结:
一、SSA(Singular Spectrum Analysis)
SSA作为一种应用广泛的算法,网上已经有了很多详细的资料可以参考,这里将步骤进行简单总结。
(1)构建轨迹矩阵
选择合适的窗口长度M,M的选取依照经验应该在区间(1,N/2)内,并且最好为周期的整数倍,这里N是一维时间序列的长度,构建的形式如下:
原始序列:
X
i
=
[
X
1
,
X
2
,
X
3
,
…
,
X
n
]
X_i = \left[ X_1,X_2,X_3,{\ldots} ,X_n \right]
Xi=[X1,X2,X3,…,Xn]
轨迹矩阵:
X
M
K
=
[
X
1
,
X
2
,
X
3
,
…
,
X
K
]
=
[
X
1
X
2
…
X
N
−
M
+
1
X
2
X
3
…
X
N
−
M
+
2
⋮
⋮
⋱
⋮
X
M
X
M
+
1
…
X
N
]
X_{MK} = \left[ X_1,X_2,X_3,{\ldots} ,X_K \right] \\ \qquad\qquad\qquad\ \ \ \ = \begin{bmatrix} X_1&X_2&{\ldots} &X_{N-M+1}\\ X_2&X_3&{\ldots} &X_{N-M+2}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ X_M&X_{M+1}&{\ldots} &X_N \end{bmatrix}
XMK=[X1,X2,X3,…,XK] =
X1X2⋮XMX2X3⋮XM+1……⋱…XN−M+1XN−M+2⋮XN
其中:
K
=
N
−
M
+
1
K = N-M+1
K=N−M+1
(2)奇异值分解
首先根据轨迹矩阵X构造协方差矩阵S,然后对S进行SVD分解,得到S的特征值E和特征向量U,E是对角阵要按从大到小的顺序排列。
S
M
M
=
X
M
K
∗
X
K
M
T
=
U
M
M
E
M
M
V
1
S_{MM} = X_{MK} * X^T_{KM} = U_{MM}E_{MM}V_1
SMM=XMK∗XKMT=UMMEMMV1
求轨迹矩阵X对应的V值,其中d为X的秩:
V
d
m
⟹
V
i
=
X
T
∗
U
i
/
E
(
i
,
i
)
(
i
=
1
,
2
,
…
,
d
)
V_{dm}\ \ \ {\Longrightarrow}\ \ V_i = X^T*U_i/\sqrt {E(i,i)}\ \ (i=1,2,{\ldots},d)
Vdm ⟹ Vi=XT∗Ui/E(i,i) (i=1,2,…,d)
计算得到对应的d个初等矩阵,轨迹矩阵可以由d个初等矩阵X_i线性表示:
X
轨迹
=
∑
1
d
X
i
X_{轨迹} ={ \sum_1^dX_i}
X轨迹=1∑dXi
X
i
=
λ
i
U
i
/
V
i
T
λ
i
=
E
(
i
,
i
)
X_i =\sqrt { \lambda_i}U_i/V_i^T\ \ \ \ \ \lambda_i=\sqrt {E(i,i)}
Xi=λiUi/ViT λi=E(i,i)
(3)分组重构
将具有相同信号的子序列进行叠加,得到表示趋势、周期、半周期、噪声等信号的特殊序列,进而实现了对原始序列的分解。重构原理公式如下:
y
i
=
{
1
i
∑
M
=
1
K
X
M
,
i
−
M
+
1
1
≤
i
<
M
1
M
∑
M
=
1
L
X
M
,
i
−
M
+
1
M
≤
i
<
K
1
N
−
i
+
1
∑
M
=
i
−
K
+
1
N
−
K
+
1
X
M
,
i
−
M
+
1
K
≤
i
<
N
y_i = \begin{cases} \frac {1}{i}\displaystyle \sum^{ K}_{M = 1}{X_{M,i-M+1} \qquad\qquad\qquad 1\leq{i}\lt{M}}\\ \frac {1}{M}\displaystyle \sum^{ L}_{M = 1}{X_{M,i-M+1} \qquad\qquad\quad\ \ M\leq{i}\lt{K}}\\ \frac {1}{N-i+1}\displaystyle \sum^{N-K+1}_{M = i-K+1}{X_{M,i-M+1} \qquad K\leq{i}\lt{N}} \end{cases}
yi=⎩
⎨
⎧i1M=1∑KXM,i−M+11≤i<MM1M=1∑LXM,i−M+1 M≤i<KN−i+11M=i−K+1∑N−K+1XM,i−M+1K≤i<N
分组重构的关键在于区分同类信号,如果是提取特定序列可以依据加权相关(w-Correlation)进行划分,得到需要的趋势、周期等信号;如果是去噪可以根据贡献度进行重构,贡献度低的子序列认为是噪声,重构的时候忽略这部分子序列即可。
上面是奇异谱分析的原理简述仅供参考,可能有错误、缺失或其他问题。
二、代码实现及案例展示
主程序:
%% 奇异谱分析
clear;
%% 模拟时间序列,分别模拟出周期、趋势和噪声项
n = 132*5;
ntest = 48;
x = 1:n;
% 周期信号
a1 = cos(2*pi*x/12) + 0.6 * sin(2*pi*x/24);
figure(1)
subplot(2,2,1)
plot(x,a1);
title('a1 周期信号')
% 趋势信号
subplot(2,2,2);
x2=0.14;
a2 = mapminmax(x2 * x,0,1);
plot(x,a2);
title('a2 趋势信号')
% 随机信号(0-1的随机值)
subplot(2,2,3)
a3 = rand(1,n);
plot(x,a3);
title('a3 随机信号')
% 三种信号叠加 生成模拟信号
subplot(2,2,4)
a41 = 2 .* a1 + 5 * a2 + 3.2 * a3; % 3 周期 + 趋势 + 随机
plot(x,a41);
title('a4 叠加序列')
y = a41;
n = length(y); %序列长度
l = 10; %输出窗口长度L
[y1,lamuda]=SSA_function(y,n,l); %进行奇异谱分析得到L个初等矩阵
ref = 0.95;
[x] = Contribution_rate(lamuda,l,ref); %根据贡献率选择重构阶数,阈值根据需求设置
[coll] = w_collelation(y1,l,n); %权相关分析得到w-correlation图
figure(2)
heatmap(coll);
yout = zeros(1,n);
for i=1:x
yout(1,:) = yout(1,:) + y1(i,:);
end
figure(3)
plot(1:n,y,'-r',1:n,yout,'-g')
%% 输出趋势项()
prompt = '趋势项阶数: '; %根据w-collelation图输入重构阶数
x = input(prompt); %根据权重图选择要重构信号
yout = zeros(1,n);
for i=1:x
yout(1,:) = yout(1,:) + y1(i,:);
end
figure(4)
plot(1:n,yout,'-r')
%% 输出周期项
prompt = '输出周期项: '; %根据w-collelation图输入重构阶数
x2 = input(prompt); %根据权重图选择要重构信号
yout = zeros(1,n);
for i=x+1:x2
yout(1,:) = yout(1,:) + y1(i,:);
end
figure(5)
plot(1:n,yout,'-g')
%% 输出半周期项
prompt = '输出半周期项: '; %根据w-collelation图输入重构阶数
x3 = input(prompt); %根据权重图选择要重构信号
yout = zeros(1,n);
for i=x2+1:x3
yout(1,:) = yout(1,:) + y1(i,:);
end
figure(6)
plot(1:n,yout,'-g')
相关函数
%% 奇异谱分析函数
%x 原始时间序列;n一维时间序列x的维度;l窗口长度(为周期的整数倍,不超过n/2)
% 返回的y的维度是[窗口长度l*序列长度n],表示l个初等矩阵;
function [y,lamuda]=SSA_function(x,n,l)
% Step1 : 建立时滞矩阵
k1=n-l+1;
X2=zeros(l,k1);
for i=1:k1
X2(1:l,i)=x(i:l+i-1);
end
% Step 2: 奇异值分解
x3=X2*X2';
[U,S,V] = svd(x3);
for i=1:l
V1(:,i) = X2'*U(:,i)/sqrt(S(i,i));
end
%初等矩阵重构得到l个时间序列;
y = zeros(l,n);
Lp=min(l,k1);
Kp=max(l,k1);
for i=1:l
xi = sqrt(S(i,i)) * U(:,i) * V1(:,i)';
y1=zeros(n,1);
for k=0:Lp-2
for m=1:k+1
y1(k+1)=y1(k+1)+(1/(k+1))*xi(m,k-m+2);
end
end
%重构 Lp~Kp
for k=Lp-1:Kp-1
for m=1:Lp
y1(k+1)=y1(k+1)+(1/(Lp))*xi(m,k-m+2);
end
end
%重构 Kp+1~N
for k=Kp:n-1
for m=k-Kp+2:n-Kp+1
y1(k+1)=y1(k+1)+(1/(n-k))*xi(m,k-m+2);
end
end
y(i,:) = y1(:,1);
end
%将特征值输出一列
%lamuda = zeros(l,1)
for i = 1:l
lamuda(i,1) = S(i,i);
end
end
%% 权相关
function [coll] = w_collelation(y,l,n)
k = n-l+1;
coll = zeros(l,l);
for i =1:l
for j =1:l
if l<k
xfc = 0.0;
xfx = 0.d0;
xfy = 0.0;
for h=1:n
if h >= 1 && h<l
w = h;
elseif h >= l && h<k
w=l;
elseif h >= k && h<=n
w = n-h+1;
end
xfc = xfc + w*y(i,h)*y(j,h);
xfx = xfx + w *y(i,h)^2;
xfy = xfy + w * y(j,h)^2;
end
coll(i,j) = xfc/(sqrt(xfx)*sqrt(xfy));
end
end
end
end
%% 计算奇异值的贡献率
function [n,array2] = Contribution_rate(lamuda,l,ref) %输入奇异值、窗口长度、阈值(0,1)
sum1 = sum(lamuda(:));
for i=1:l
sum2 = sum(lamuda(1:i));
num = sum2/sum1;
array2(i) = num;
if num >= ref
n = i;
break
end
end
end
案例运行结果
模拟序列
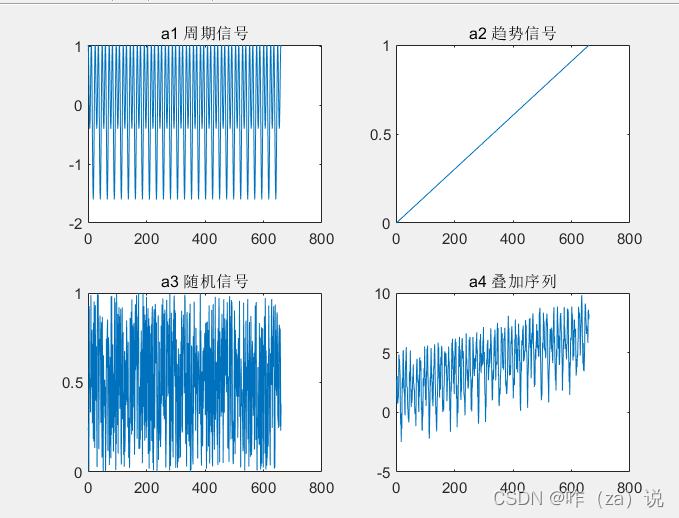
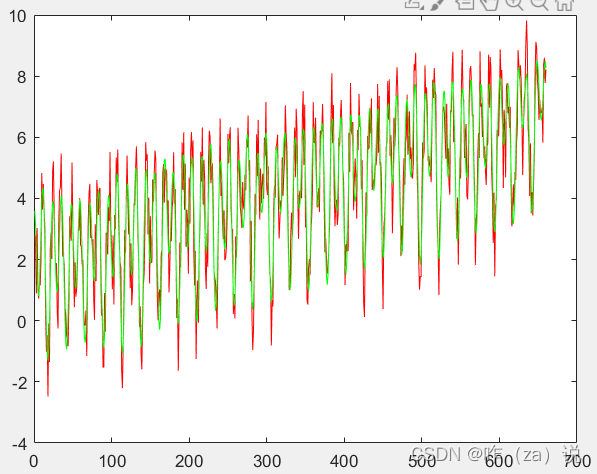
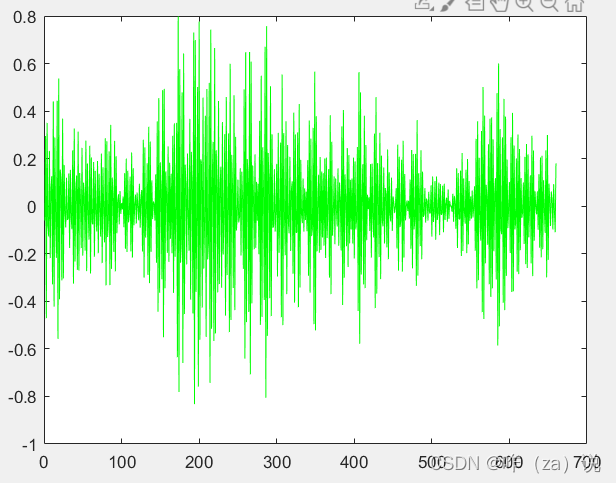
原始序列(红线)和0.95贡献率下的重构(绿线)
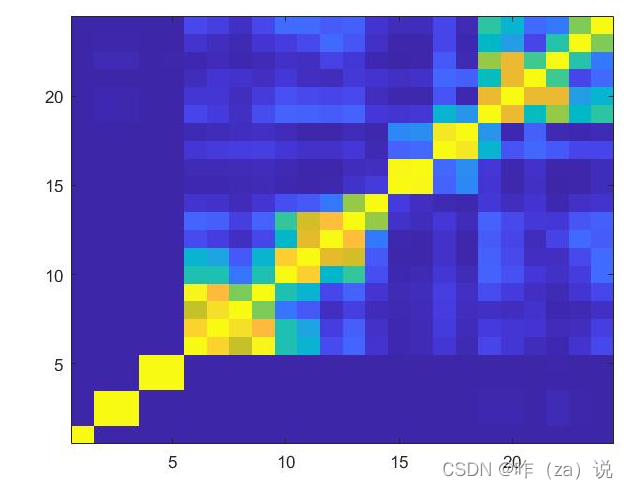
w-correlation
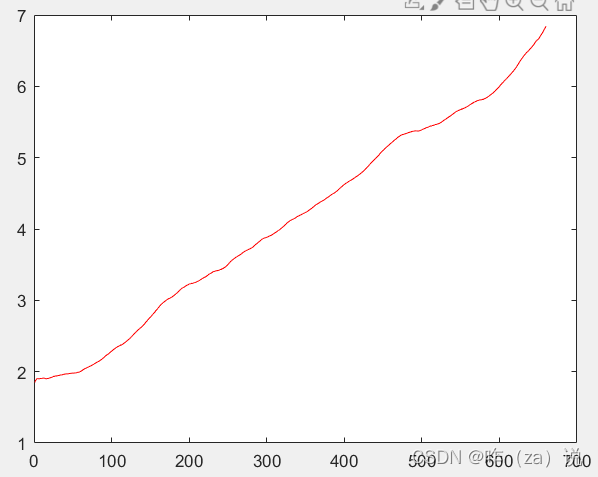
趋势项
周期项

半周期
总结
这是关于SSA自己的一些简单理解,实现过程参考了网上的一些资料,过程可能有错误自行斟酌吧。