【论文阅读笔记】Meta 3D AssetGen: Text-to-Mesh Generation with High-Quality Geometry, Texture, and PBR Materials
Info
project:https://assetgen.github.io/
paper:https://arxiv.org/abs/2407.02445
Meta 这一手有点顶,连发三篇,PBR 材质打通了我比较惊讶的是这个数据集的组织形式,怎么把材质种类划分的这么好,希望大佬指教
摘要
我们提出了 Meta 3D AsetGen (AssetGen),这是文本到 3D 生成的重大进步,它产生了忠实、高质量的网格,具有纹理和材料控制。与在 3D 对象外观中烘烤阴影的作品相比,AsetGen 输出基于物理的渲染 (PBR) 材料,支持逼真的重新照明。AsetGen 使用分解阴影和反照率外观通道生成对象的前几个视图,然后使用延迟阴影损失重建 3D 中的颜色、金属度和粗糙度以进行有效监督。它还使用符号距离函数更可靠地表示 3D 形状,并为直接形状监督引入了相应的损失。这是使用融合内核实现的,以实现高内存效率。在网格提取之后,在UV空间中操作的纹理细化转换器显著提高了清晰度和细节。AsetGen 在倒角距离方面提高了 17%,在 LPIPS 中比用于少视图重建的最佳并行工作提高了 40%,人类对可比速度的最佳行业竞争对手的偏好为 72%,包括那些支持 PBR 的人。
引言
- PBR 材质的重要性
- AsetGen 在 30 秒以下生成资产,同时优于先前在忠实度、生成的 3D 网格质量以及材料的质量和控制方面相当速度的工作,支持基于物理的渲染 (PBR) [85]。
- AsetGen 使用受 [40] 启发的两阶段设计。第一阶段从4个规范视点随机生成对象的4个图像,第二阶段确定性地从这些视图中重建对象的3D形状和外观(图1)。这种方法比基于 SDS 的技术 [66] 更快、更稳健,并且比单级 3D 生成器产生更多样化和更忠实的结果 [36, 59, 92, 77]。
创新点
我们考虑了反照率、金属度和粗糙度来渲染准确反映环境照明的场景。此外,由于网格在应用程序和与 PBR 的兼容性方面的流行,我们专注于网格作为输出表示。
- 我们的第一个贡献是扩展两个阶段以生成 PBR 信息。由于图像到 3D 阶段是确定性的,它是文本到图像阶段,它是随机的,应该解决分配材料的歧义。这可以通过微调文本到图像模型来直接输出所需的 PBR 通道来完成,但由于 PBR 和自然图像之间的差距很大,我们发现这是有问题的。相反,我们为文本到图像模型分配了更简单的任务,即输出外观的阴影和反照率(无阴影)版本。这允许图像到 3D 组件通过分析反照率和阴影通道之间的差异来准确预测 PBR 材料。
- 我们的第二个创新在于网格生成步骤。现有的工作通常输出一个不透明度场来表示 3D 形状,但后者可能会导致定义不明确的水平集,从而导致网格伪影。为了解决这个问题,AsetGen 的图像到 3D 阶段 MetaILRM 直接预测符号距离场 (SDF) 而不是不透明度场。这会产生更高质量的网格,因为SDF的零水平集更可靠地跟踪对象的表面。此外,这种表示可以很容易地使用地面真实深度图进行监督,这对于不透明度来说是不可能的。我们使用VolSDF[107]来不同地渲染基于SDF的模型,并通过在内存高效的LightPlane Kernels[6]中实现渲染来提高训练效率。这允许对高分辨率渲染进行更大的批次和光度损失监督,从而获得更好的纹理质量。
挖个坑,解读一下LightPlane
相关工作
T23D
受文本到图像模型的启发,早期的文本到 3D 方法 [62, 33 , 26 , 109 , 104 ] 在字幕 3D 资产的数据集上训练 3D 扩散模型。然而,3D 数据的有限大小和多样性阻碍了对开放词汇提示的泛化。因此,最近的工作基于在数十亿个字幕图像上训练的文本到图像模型的此类生成器。2 其中,[73]、54等工作微调2D扩散模型输出3D表示,但由于2D-3D域间隙较大,质量有限。其他方法可以深入研究两组。
- 第一组包含基于DreamFusion的方法,这是[66]的开创性工作,并通过SDS损失优化NeRF来提取3D对象,将其渲染与预先训练的文本到图像模型的信念相匹配。考虑了扩展:(i)其他3D表示,如哈希网格[42,67]、网格[42]和3D高斯(3DGS)[7,110,12,12];(ii)改进的SDS[89,93,118,30];(iii)单眼条件反射[67,80,112,76];(iv)预测额外的法线或深度以获得更好的几何形状[68,76]。然而,蒸馏方法容易出现Janus效应(复制对象部分)和内容漂移等问题[72]。一种常见的解决方案是通过将视图一致性先验合并到扩散模型中,通过对相机[45,71,31,11,67]进行调节,或者通过联合生成多个对象视图[72,96,91,38,17]。此外,SDS 优化很慢,每个资产需要几分钟到小时;这个问题在 [50, 99] 中部分解决,带有摊销 SDS。
- 第二组方法包括更快的两阶段方法[44,49,47,106,105,8,81,28,23],它首先使用文本到图像或视频模型[52,13]生成对象的多个视图,然后使用NERF[56]或3DGS[37]进行逐场景优化。然而,每个场景的优化需要几个高度一致的视图,这些视图很难可靠地生成。Instant3D[40]通过生成仅四个视图的网格和从这些视图重建对象的前馈网络(LRM[29])来提高速度和稳健性。One-2-3-45++ [43] 将 LRM 替换为 3D 扩散模型。
我们的 AsetGen 建立在 Instant3D 范式之上,并将 LRM 升级为输出 PBR 材料和基于 SDF 的 3D 形状的表示。此外,它从四个带有阴影和反照率通道的视图网格开始,这是从图像中预测准确的3D形状和材料的关键。
基于图片的3d 重建
从图像中重建3D。3D场景重建,在传统的多视图立体(MVS)意义上,假设可以访问密集的场景视图集。最近的重建方法,如NeRF[56],通过最小化多视图渲染损失来优化3D表示。
有两种流行的3D表示类:(i)网格[22,13,24,61,57,74]或3D点/高斯[37,25]等显式表示,以及(ii)占用场[63]、亮度场[56,60]和符号距离函数(SDF)[108]等隐式表示。与占用场相比,SDF[64,107,90,17,21]简化了表面约束集成,提高了场景几何。出于这个原因,我们采用了 SDF 公式并证明它优于占用率。
相反,稀疏视图重建假设输入视图很少(通常为 1 到 8)。减轻密集多个视图缺乏的一种方法是在优化过程中利用 2D 扩散先验 [53, 97],但这通常很慢并且不是很健壮。最近,作者专注于在大型数据集上训练前馈重构器[14,35,55,46,98,58,92]。特别是,最先进的LRM[29]训练一个大的Transformer[87],使用三平面表示来预测NeRF[7,9]。LRM扩展研究其他3D表示,如网格[101,95]和3DGS[119,103,78,114],改进的骨干[94,95]和训练协议[84,34]。
我们的方法还建立在 LRM 之上,但引入了三个关键修改:(i)改进几何形状的 SDF 公式,(ii)重新照明的 PBR 材料预测,以及(iii)纹理细化器以获得更好的纹理细节。
使用 PBR 材料的 3D 建模。
大多数 3D 生成器输出具有烘烤照明的 3D 对象,无论是视图相关的 [56, 37] 还是与视图无关的 [29]。由于烘焙照明忽略了模型对环境照明的响应,不适合具有受控照明的图形管道。**基于物理的渲染(PBR)定义了材料属性,以便合适的着色器可以真实地解释照明。**一些MVS工作考虑了使用NeRF[4,3,100]、SDF[115]、可微网格[61,27]或3DGS[32,41]估计PBR材料。在生成建模中,[10,68,48,102]使用PBR模型增强了文本到3D SDS优化[66]。与它们不同的是,我们将 PBR 建模集成到我们的前馈文本到 3D 网络中,首次解锁了具有可控 PBR 材料的基于快速文本生成 3D 资产。
方法
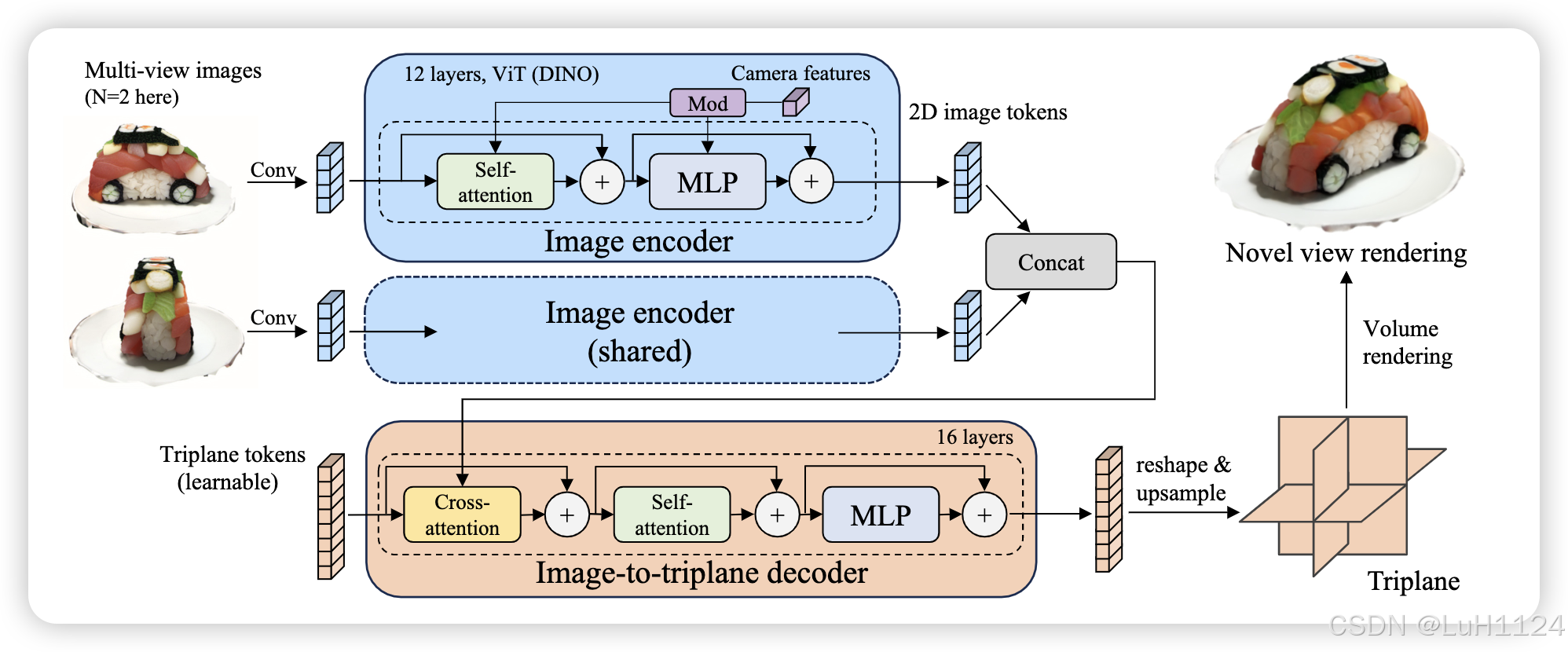
AsetGen 是一个两阶段管道(图 2)。首先,文本到图像(第3.1节),将文本作为输入,生成具有材料信息的4视图图像网格。其次,图像到 3D 包括一种新颖的基于 PBR 的稀疏视图重建模型(第 3.2 节)和纹理细化器(第 3.3 节)。因此,AsetGen 适用于两个任务:text-to-3D(阶段 1+2)和image-to-3D(仅阶段 2)。
文本到图像:从文本中生成阴影和反照率图像
类似于MVDREAM 和 Instant3D,首先 fintuene 了一个生成四视角的模型。但是发现如果直接预测 PBR 材质(abeldo、roughness、metallic)无法收敛,转而去预测abeldo和 shading降低难度(输入输出改为 6 通道)
Image-to-3D:基于pbr的大型重构模型
训练 MetalLRM,输入是6 通道图像,借助 Triplane 后面接两个 MLP 分别预测 SDF
R
3
−
>
R
R^3->R
R3−>R和PBR系数
R
3
−
>
R
5
R^3->R^5
R3−>R5 (abeldo、roughness、metallic)
k
(
x
)
=
(
ρ
0
,
γ
,
α
)
are the albedo, metalness and roughness.
k(\boldsymbol{x})=\left(\rho_{0}, \gamma, \alpha\right) \text { are the albedo, metalness and roughness. }
k(x)=(ρ0,γ,α) are the albedo, metalness and roughness.
学习模型的关键是可微分渲染算子 R。这将场
ℓ
:
R
3
→
R
D
\ell: \mathbb{R}^{3} \rightarrow \mathbb{R}^{D}
ℓ:R3→RD、SDF
s
s
s、视点
π
π
π和像素
u
∈
U
=
[
0
,
W
)
×
[
0
,
H
)
u∈U = [0, W) × [0, H)
u∈U=[0,W)×[0,H)作为输入,并根据渲染方程[56]输出场在像素上的投影,该渲染方程具有与渲染场ℓ相同数量的通道D:
R
(
u
∣
ℓ
,
s
,
π
)
=
∫
0
∞
ℓ
(
x
t
)
σ
(
x
t
∣
s
)
e
−
∫
0
t
σ
(
x
τ
∣
s
)
d
τ
d
t
.
(
1
)
\mathcal{R}(u \mid \ell, s, \pi)=\int_{0}^{\infty} \ell\left(\boldsymbol{x}_{t}\right) \sigma\left(\boldsymbol{x}_{t} \mid s\right) e^{-\int_{0}^{t} \sigma\left(\boldsymbol{x}_{\tau} \mid s\right) d \tau} dt . (1)
R(u∣ℓ,s,π)=∫0∞ℓ(xt)σ(xt∣s)e−∫0tσ(xτ∣s)dτdt.(1)
这里 xt = x0 - tωo, t ∈ [0, ∞) 是沿方向
−
ω
o
∈
S
2
-ω_o ∈ S^2
−ωo∈S2 的像素 u 从相机中心
x
0
x_0
x0 到射线。函数 σ(x | s) 是 3D 点 x 的不透明度,使用VolSDF[107]公式从SDF值s(X)得到:
σ
(
x
∣
s
)
=
a
2
(
1
+
sign
s
(
x
)
(
1
−
e
−
∣
s
(
x
)
∣
/
b
)
)
,
\sigma(\boldsymbol{x} \mid s)=\frac{a}{2}\left(1+\operatorname{sign} s(\boldsymbol{x})\left(1-e^{-|s(\boldsymbol{x})| / b}\right)\right),
σ(x∣s)=2a(1+signs(x)(1−e−∣s(x)∣/b)),
其中 a, b 是超参数。
反射模型
阴影RGB图像
I
^
\hat I
I^中的对象
I
^
(
U
)
=
R
(
u
∣
L
,
s
,
π
)
\hat I(U)=R(u|L,s,π)
I^(U)=R(u∣L,s,π)的外观是通过渲染其辐射场
ℓ
(
X
)
=
L
(
x
,
ω
o
∣
k
,
n
)
ℓ(X)=L(x,ω_o|k,n)
ℓ(X)=L(x,ωo∣k,n)来获得的,其中n是单位法线的场。亮度是物体在观察者方向
ω
o
ω_o
ωo反射的光(见App.A.8 的详细信息),其中 PBR 由下式给出:
L
(
x
,
ω
o
∣
k
,
n
)
=
∫
H
(
n
)
f
(
ω
i
,
ω
o
∣
k
(
x
)
,
n
(
x
)
)
L
(
x
,
−
ω
i
)
(
n
(
x
)
⋅
ω
i
)
d
Ω
i
(
3
)
L\left(\boldsymbol{x}, \boldsymbol{\omega}_{\mathrm{o}} \mid k, \boldsymbol{n}\right)=\int_{H(\boldsymbol{n})} f\left(\boldsymbol{\omega}_{\mathrm{i}}, \boldsymbol{\omega}_{\mathrm{o}} \mid k(\boldsymbol{x}), \boldsymbol{n}(\boldsymbol{x})\right) L\left(\boldsymbol{x},-\boldsymbol{\omega}_{\mathrm{i}}\right)\left(\boldsymbol{n}(\boldsymbol{x}) \cdot \boldsymbol{\omega}_{\mathrm{i}}\right) d \Omega_{\mathrm{i}} (3)
L(x,ωo∣k,n)=∫H(n)f(ωi,ωo∣k(x),n(x))L(x,−ωi)(n(x)⋅ωi)dΩi(3)
其中
ω
o
,
ω
i
∈
H
(
n
)
=
ω
∈
S
2
:
n
⋅
ω
≥
0
ω_o, ω_i ∈ H(n) = {ω ∈ S2 : n · ω ≥ 0}
ωo,ωi∈H(n)=ω∈S2:n⋅ω≥0是指向对象外部的两个单位向量,
L
(
x
,
−
ω
i
)
L(x, −ω_i)
L(x,−ωi) 是从 x 处的环境在立体角
d
Ω
i
dΩ_i
dΩi 中从方向
ω
i
ω_i
ωi 入射的辐射。双向反射分布函数 (BRDF) f 告诉从方向
−
ω
i
-ω_i
−ωi(传入)接收到的光如何被对象 [20] 分散到不同的方向
ω
o
ω_o
ωo(传出)
在PBR中,我们考虑了BRDF的物理启发模型,在真实感和复杂性之间取得平衡[2,85,75,15,88];具体来说,我们使用迪士尼GGX模型[88,5],它只依赖于参数 ρ 0 、 γ 和 α ρ_0、γ和α ρ0、γ和α(见App.A.12.1 用于 f 的参数形式)。因此,MetaI LRM 在每个 3D 点 x 处预测三元组 k ( x ) = ( ρ 0 , γ , α ) k(x) = (ρ_0, γ, α) k(x)=(ρ0,γ,α)。
延迟着色
在实践中,我们不是使用方程式(1),(3)计算
I
^
(
u
)
=
R
(
u
∣
L
,
s
,
π
)
\hat{I}(u)=\mathcal{R}(u \mid L, s, \pi)
I^(u)=R(u∣L,s,π),我们使用延迟着色过程 [20]:
I
^
(
u
)
=
R
def
(
u
∣
k
,
s
,
π
)
=
∫
H
(
n
)
f
(
ω
i
,
ω
o
∣
k
ˉ
,
n
‾
)
L
e
n
v
(
−
ω
i
)
(
n
‾
⋅
ω
i
)
d
Ω
i
,
(
4
)
\hat{I}(u)=\mathcal{R}_{\operatorname{def}}(u \mid k, s, \pi)=\int_{H(\boldsymbol{n})} f\left(\boldsymbol{\omega}_{\mathrm{i}}, \boldsymbol{\omega}_{\mathrm{o}} \mid \bar{k}, \overline{\boldsymbol{n}}\right) L_{\mathrm{env}}\left(-\boldsymbol{\omega}_{\mathrm{i}}\right)\left(\overline{\boldsymbol{n}} \cdot \boldsymbol{\omega}_{\mathrm{i}}\right) d \Omega_{\mathrm{i}}, \text(4)
I^(u)=Rdef(u∣k,s,π)=∫H(n)f(ωi,ωo∣kˉ,n)Lenv(−ωi)(n⋅ωi)dΩi,(4)
其中 L e n v L_{env} Lenv是环境辐射度(假设所有x都假定相同),̄ k ˉ = R ( u ∣ k , s , π ) \bar{k}=\mathcal{R}(u \mid k, s, \pi) kˉ=R(u∣k,s,π)和̄ n ‾ = R ( u ∣ n , s , π ) \overline{\boldsymbol{n}}=\mathcal{R}(u \mid \boldsymbol{n}, s, \pi) n=R(u∣n,s,π)是材质和法线场的渲染。Eq.(4)的优点是,在Eq.(1)的评估过程中,BRDF f f f只评估每个像素一次,这比对每个3D点这样做要快得多,内存密集更少,特别是对于训练/反向传播。此外,在训练过程中,假设环境光是无穷远处的单个光源,因此积分(4)简化为评估单个项。
延迟着色方法,是先把场景中所有物体渲染一次,将其相关数据(包括位置、法向量、纹理等)保存到一个帧缓存中,然后,用这些数据配合上光源信息再进行一次计算,得到最终的效果。
loss
因此,MetaILRM 是一个神经网络,它将一组图像 ( I i , π i ) i = 1 N \left(I_{i}, \pi_{i}\right)_{i=1}^{N} (Ii,πi)i=1N作为输入,并为 SDF 和 PBR 字段输出估计 s ^ \hat s s^和 k ^ \hat k k^。
我们从网格表面数据集 M ⊂ R 3 M ⊂ R^3 M⊂R3 和地面实况 PBR 材料 k : M → R 5 . k: M \rightarrow \mathbb{R}^{5} \text {. } k:M→R5. 对其进行训练。
重建模型通常通过对渲染的监督进行训练[29,95]。然而,通过方程式进行物理上准确的渲染。 (1) 非常昂贵。我们以两种方式克服了这个障碍。首先,我们渲染原始的ground-truth PBR字段 k k k,并使用它们来监督其MSE损失的预测对应项,跳过Eq.(1)。对于与自然图像足够相似的渲染反照率 ρ 0 ρ_0 ρ0,我们也使用LPIPS[116]损失:
L p b r = LPIPS ( R ( ⋅ ∣ ρ ^ 0 , s ^ , π ) , R ( ⋅ ∣ ρ 0 , M , π ) ) + ∥ R ( ⋅ ∣ k ^ , s ^ , π ) − R ( ⋅ ∣ k , M , π ) ∥ 2 . \mathcal{L}_{\mathrm{pbr}}=\operatorname{LPIPS}\left(\mathcal{R}\left(\cdot \mid \hat{\rho}_{0}, \hat{s}, \pi\right), \mathcal{R}\left(\cdot \mid \rho_{0}, M, \pi\right)\right)+\|\mathcal{R}(\cdot \mid \hat{k}, \hat{s}, \pi)-\mathcal{R}(\cdot \mid k, M, \pi)\|^{2} . Lpbr=LPIPS(R(⋅∣ρ^0,s^,π),R(⋅∣ρ0,M,π))+∥R(⋅∣k^,s^,π)−R(⋅∣k,M,π)∥2.
我们通过添加计算效率高的延迟阴影损失来进一步监督 PBR 字段:
L
def
=
∥
w
⊙
(
R
d
e
f
(
⋅
∣
k
^
,
s
^
,
π
)
−
R
d
e
f
(
⋅
∣
k
,
M
,
π
)
)
∥
2
\mathcal{L}_{\text {def }}=\left\|\sqrt{w} \odot\left(\mathcal{R}_{\mathrm{def}}(\cdot \mid \hat{k}, \hat{s}, \pi)-\mathcal{R}_{\mathrm{def}}(\cdot \mid k, M, \pi)\right)\right\|^{2}
Ldef =
w⊙(Rdef(⋅∣k^,s^,π)−Rdef(⋅∣k,M,π))
2
权重
w
(
u
)
=
n
^
(
u
)
⋅
n
(
u
)
w(u) = \hat n(u) · n(u)
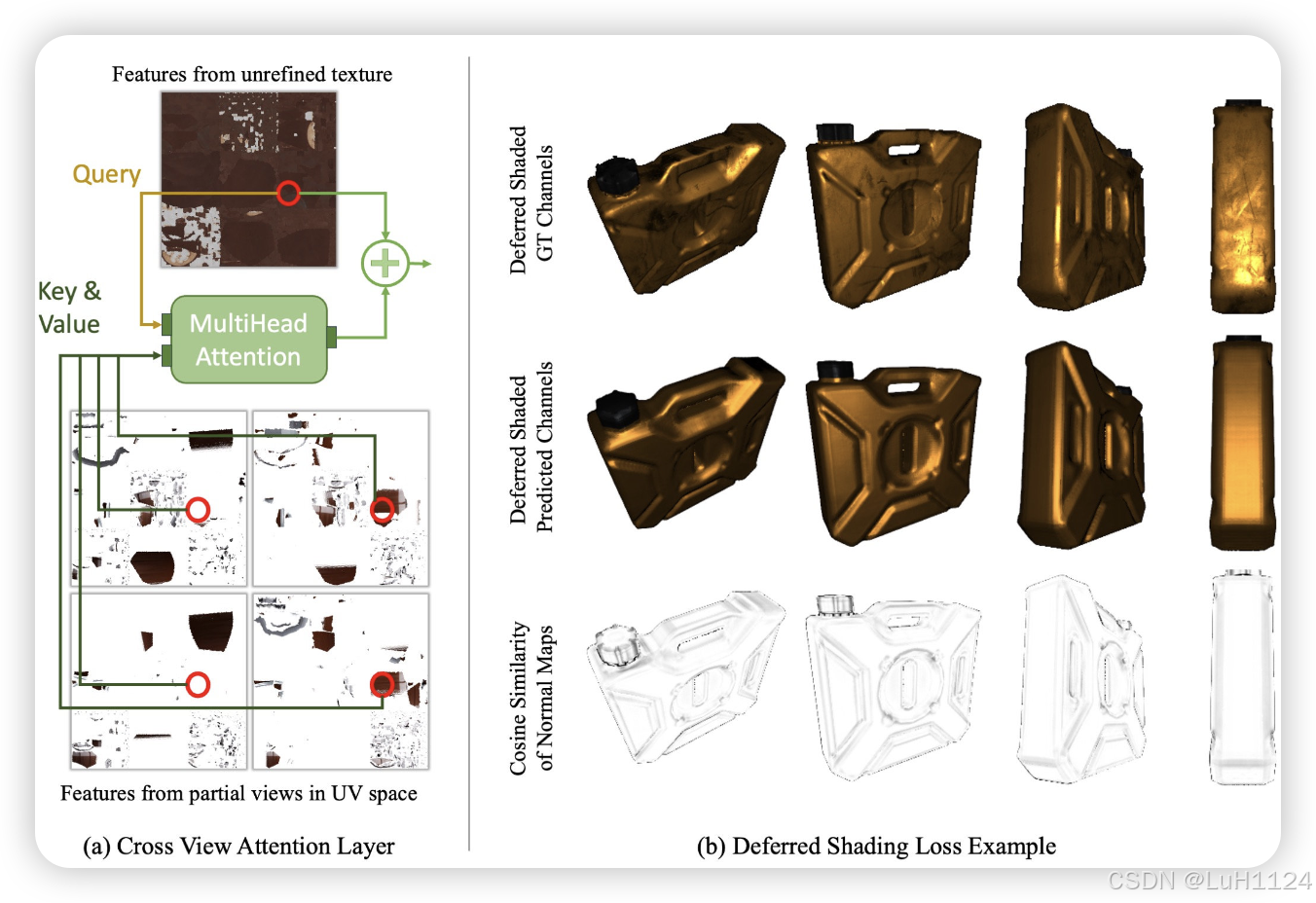
w(u)=n^(u)⋅n(u) 是像素 u 处预测法线和真实法线的点积。它忽略了尚未学习的预测几何体的损失。图 13 (b) 可视化了延迟阴影和渲染损失。
最后,我们还使用直接损失 L s d f L_{sdf} Lsdf来监督SDF场(如[1]所示),深度渲染与地面真实之间的深度MSE损失 L d e p t h L_{depth} Ldepth,并在 a l p h a alpha alpha掩码渲染和真实掩码之间使用二元交叉熵 L m a s k L_{mask} Lmask。参考appendix.6.2 了解更多详细信息。
LightPlane实现
我们将 MetaILRM 建立在 LightplaneLRM [6] 上,这是 LRM [29] 的一种变体,它利用内存和计算高效的 Lightplant splatting 和渲染内核,提供更好的质量重建。然而,由于LightplaneLRM使用密度场,这对于网格转换来说是次优的[90,64,1],我们使用Eq.(2)使用VolSDF[107]渲染器扩展了Lightplane渲染器GPU内核。此外,我们还将直接 SDF 损失 L s d f L_{sdf} Lsdf 融合到内核中,因为朴素的 autograd 实现太耗费内存了。
网格提取和纹理细化器
第3.2节的MetaILRM模块输出一个符号距离函数s,隐式定义对象表面 A = x ∈ R 3 ∣ s ( x ) = 0 A = {x∈R3 | s(x) = 0} A=x∈R3∣s(x)=0作为s的水平集。我们使用 Marching Tetrahedra 算法 [18] 来跟踪水平集并输出网格 M ≈ A。然后,xAtlas[111]提取UV映射φ:[0,V]2→M,将每个2DUV空间点v=φ(X)映射到网格上的点x∈M。
接下来,目标是提取一个高质量的5通道PBR纹理图像̄K∈RV ×V ×5,捕捉每个网格点的反照率、金属度和粗糙度。纹理图像 K 可以通过将预测的 PBR 场 k ^ \hat k k^ 采样为 K ( v ) ← k ^ ( φ ( v ) ) K(v) ← \hat k (φ(v)) K(v)←k^(φ(v))来直接定义,但由于 MetaILRM 的分辨率有限,这通常会产生模糊的结果。相反,我们设计了一个纹理细化器模块,该模块将粗略的 PBR 采样纹理图像作为输入,以及表示对象的 N 个视图并输出更清晰的纹理 k ˉ \bar k kˉ。本质上,该模块利用来自不同视图的信息来细化粗纹理图像。图 2 的右侧部分说明了该模块。
更具体地说,它依赖于输入 N + 1 个纹理图像 {Ki}N i=0 的网络 Φ。首先,K0 ∈ RV ×V ×11 的每个像素 v ∈ [0, V ]2 用法线、3D 位置和 MetaILRM 的 PBR 场 k(φ(v)) 的输出在 v 的 3D 点 φ(v) 上进行评估。剩余的 K1,。, KN 对应于具有 6 个通道的部分纹理图像(对于基本颜色和阴影颜色),这些图像是通过将对象视图反向投影到网格表面来获得的。
网络Φ利用两个U-Nets将 K i i = 0 N {K_i}^N_{i=0} Kii=0N融合到增强纹理̄K中。Φ 的目标是为每个 UV 点 v 选择 N 个输入视图中的哪一个提供了最佳信息。具体来说,每个部分纹理图像 K i K_i Ki 由第一个 U-Net 并行处理,得到的信息通过交叉注意力传达给第二个 U-Net,其目标是将 K 0 K_0 K0细化到增强的纹理 k ˉ \bar k kˉ 中。请参阅应用程序。A.7 了解更多详细信息。
这样的网络在相同的数据集上进行训练,并使用 PBR 和反照率渲染损失作为 MetaILRM 进行监督。唯一的区别是网格(其几何形状是固定的)使用 PyTorch3D 的 [69] 网格光栅化器而不是 Lightplane SDF 渲染器以不同的方式渲染。
实验
我们的训练数据由3D艺术家创建的包含140,000个不同语义类别的网格组成。对于每个资产,我们在对象周围在[-30°, 50°]范围内的随机仰角处以30°的均匀间隔渲染36个视图,并使用随机选择的环境贴图进行照明。我们从每个视角渲染阴影图像、反照率、金属度、粗糙度、深度图和前景掩模。文本到图像阶段基于一个内部文本到图像模型,结构上类似于Emu [16],在部分包含由类似Cap3D管道[51]使用Llama3 [86]的进行标题的高质量3D样本子集(10,000个)微调。另一个阶段则利用整个3D数据集。
为了评估,在[103,101,40]之后,我们使用渲染图像和地面真实图像之间的PSNR和LPIPS[116]来评估视觉质量。PSNR 在前景区域计算,以避免由于背景空而导致的度量膨胀。几何质量由渲染深度图和真实深度图(前景像素)之间的 L1 误差以及对象轮廓的 IoU 来衡量。我们进一步报告了倒角距离(CD)和正常正确性(NC)在预测和地面真实形状上均匀采样的2W 个点。用LPIPS和PSNR对反照率图像进行材料分解,对金属度和粗糙度通道进行PSNR评估。所有指标都是在网格化输出上计算的,而不是神经渲染上计算的。
稀疏视角重建
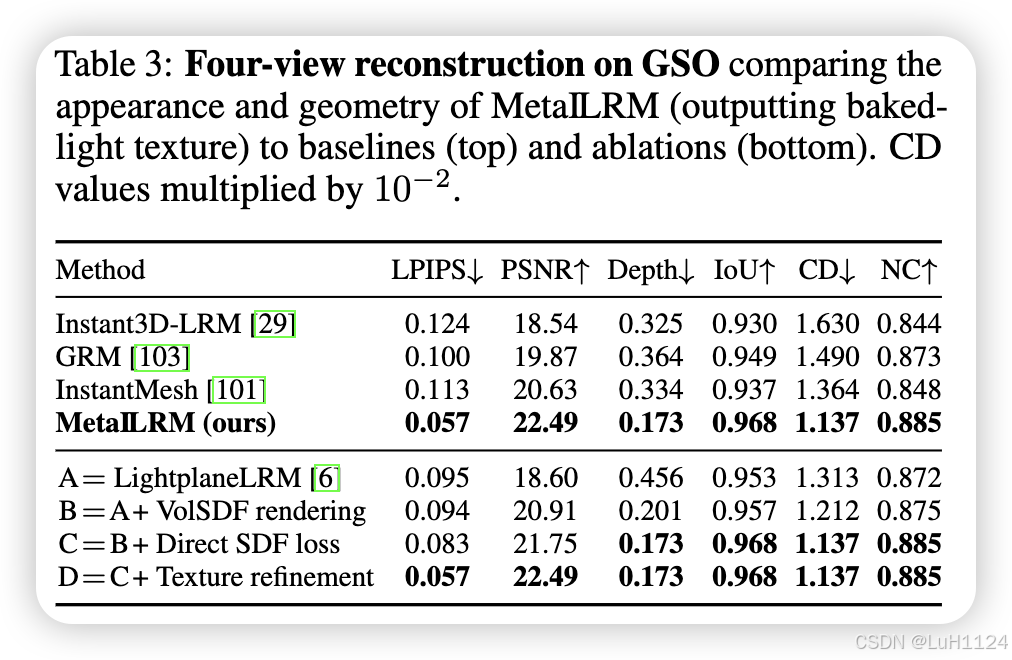
我们解决了稀疏视图重建任务,即从 Google Scanned Objects (GSO) [19] 的 332 个网格子集上从对象的 4 个姿势图像预测 3D 网格。我们与最先进的Instant3D-LRM[40]、GRM[103]、InstantMesh[101]和MeshLRM[95]进行了比较。我们还包括 LightplaneLRM [6],这是一个改进的 Instant3DLRM 版本,作为我们的基础模型。MeshLRM [95] 尚未开源,因此我们仅将它们的网页定性地与网格进行比较。所有方法都使用相同的输入视图以 51 2 2 512^2 5122 分辨率进行评估。由于后者都没有预测 PBR 材料,并且由于 GSO 缺乏真实的 PBR 材料,为了公平起见,我们使用了我们模型的变体来预测阴影对象纹理。
Figure3和Table3还展示了进一步的消融实验
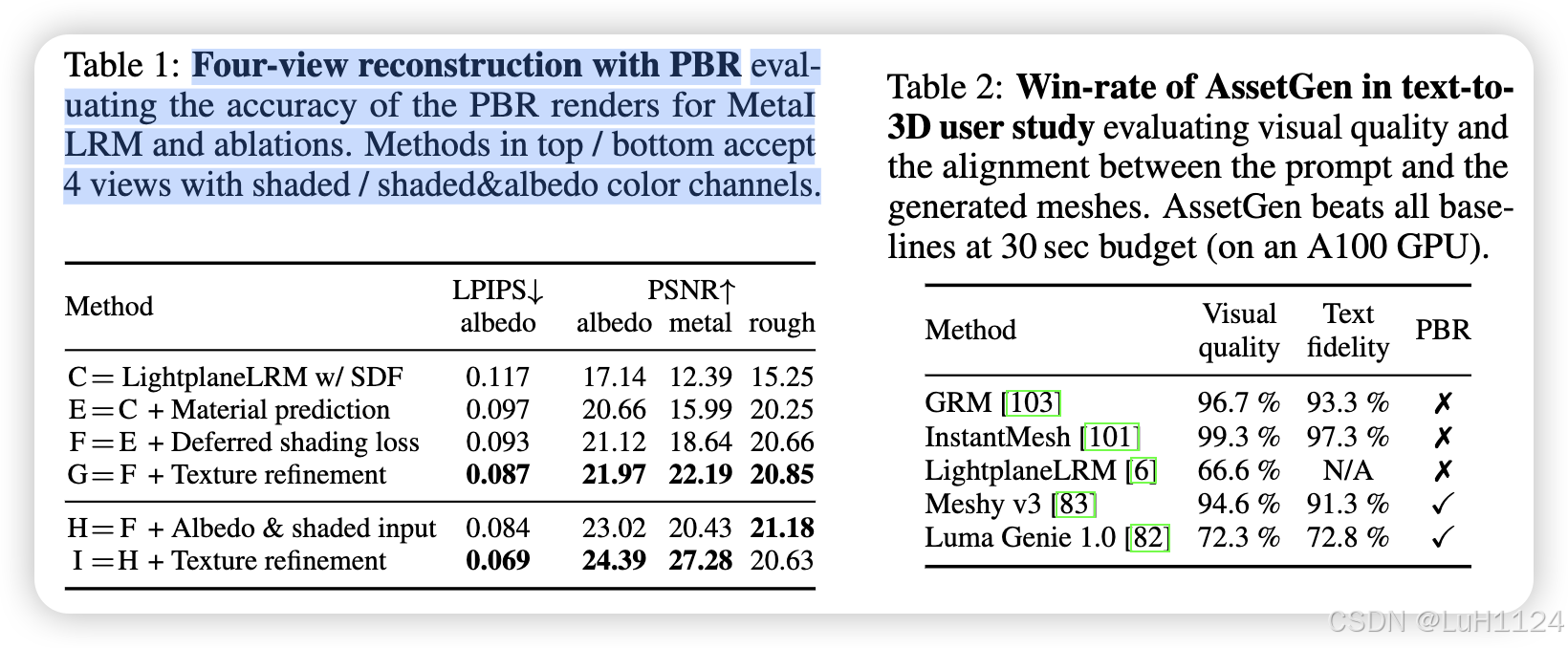
接下来,我们考虑使用 PBR 材料进行稀疏视图重建的任务,其目标是从对象的四个姿势阴影 2D 视图重建 3D 几何和纹理属性(反照率、金属度和粗糙度)。这是在 256 个艺术家创建的 3D 网格的内部数据集上进行的,这些数据集是为高质量的材料策划的。**由于不存在现有的少视图前馈 PBR 重构器,我们在 Tab 1 中进行了消融研究和图3 、图 12。**虽然添加额外的 MLP 头添加材料预测提供了一些改进,但我们观察到结合延迟阴影损失和纹理细化对于高质量的 PBR 分解至关重要。示例 PBR 预测如图 8 所示。
Text-to-3D生成
最后,我们使用 PBR 材料评估文本到 3D。我们与最先进的前馈方法进行了比较,这些方法以相当的速度生成资产(每个资产约为 10 到 30 秒)。这包括GRM[103]、InstantMesh[101]和LightplaneLRM[6]的文本到3D变体。GRM 使用 Instant3D 的 4 视图网格生成器,InstantMesh 从我们的 2D 扩散模型接收第一个视图,然后生成 6 个视图,而 LightplaneLRM 从我们的网格生成器接受 4 个视图。因为这些方法烘烤照明而不是生成 PBR 材料,为了评估,我们将平面纹理阴影应用于我们的输出【我理解是shade乘以abeldo】。此外,我们与Meshy v3[83]和LumaAI Genie 1.0[82]的预览阶段进行了比较,PBR工作流的专有文本到3D方法分别在30和15秒内创建资产。附录中提供了与 Luma 和 Meshy 的明显更长的细化阶段的比较。图5显示AssetGen网格在视觉上更具吸引力,具有有意义的材料图6和图11提供了更多的示例和比较,并展示了细粒度的材料控制。对于定量评估,我们在 Tab 中进行了广泛的用户研究。2使用来自DreamFusion[66]的404个去重文本提示。**用户展示了生成网格和基线网格的 360° 视频,并要求他们根据 3D 形状质量和与文本提示对齐对它们进行评分。共收集了 11,080 个响应,对 AsetGen 的网格有显着偏好。**最后,我们消融了与图 3 中仅反照率输入相比生成双通道反照率+阴影网格的效果,揭示了前者的显着 PBR 分解优势。此外,图 12 说明了我们的延迟阴影损失的影响。
总结
我们介绍了 Meta 3D AsetGen,这是稀疏视图重建和文本到 3D 的重大进步。Meta 3D AsssetGen可以生成具有高质量纹理和忠实于输入文本的PBR材料的3D网格。这使用了几个关键的创新:生成具有阴影通道和反照率通道的多视图网格,引入了一种新的重建网络,该网络使用延迟阴影来训练该网络,通过新的可扩展的基于SDF的渲染器和SDF损失来改进几何图形,并引入新的纹理细化网络。综合评估和消融证明了这些设计选择和最先进的性能的有效性。
附录
限制
Meta 3D AsssetGen 显着提高了形状生成,但面临几个限制。尽管对多视图图像网格生成器进行微调以进行视图一致性,但不能保证它,可能会影响 3D 重建质量。由于我们使用SDF作为底层表示,重构器可能会错误地模拟半透明对象或薄结构,如头发或毛皮。此外,虽然我们的可伸缩Triton[65]实现支持分辨率为128×128的三平面表示,但这种表示是低效的,因为它的大部分容量用于空区域。未来的工作可以探索可扩展的表示,例如八叉树、稀疏体素网格和基于哈希的方法,这可能会消除对单独纹理增强模型的需求。我们还只预测反照率、金属度和粗糙度,而不是发射率或环境遮挡。最后,我们的方法仅在对象级重建上进行了测试,为未来的研究留下了场景尺度的 3D 生成。
额外的定性实验
本节描述了额外的定性比较,由于空间有限,无法包含在主要论文中。首先,请参考补充材料中附的视频,提供 Meta 3D AsetGen 定性结果的整体呈现。在图7中,我们强调了MetaILRM在几何、纹理和材料重建中的作用。在图 11 中,我们通过更改相同概念的文本提示来可视化 Meta 3D AsetGen 提供的材料的控制,即金属度和粗糙度。图 8 显示了在给定四个输入测试视图的情况下使用 MetaILRM 提取的材料图的渲染。在图 9 中,我们提供了与 MeshLRM 更广泛的定性比较,这是最强的少视图重建基线。最后,图 6 提供了一组文本条件生成,描述了 Blender 阴影渲
染以及渲染的 PBR 图。
额外的文生3D比较
Tab2 将 Meta 3D AsetGen 的文本到 3D 代与几个快速基线进行比较,为了完整起见,本节包括与明显较慢的方法进行比较。更具体地说,我们进行了与 Tab 相同的用户研究。2 但我们比较了行业基线 Meshy v3 和 Luma Genie 的“细化”阶段,其资产生成时间分别为 5 分钟和 10 分钟。标签。4 包含用户研究的结果。Meta 3D AsssetGen 在文本保真度和视觉质量方面都显着优于 Meshy,同时速度提高了 10 倍。令人惊讶的是,Meta 3D AsetGen 在文本保真度方面与 Luma Genie 相当,在视觉质量的 40% 的情况下获胜。考虑到 Meta 3D AsetGen 的 20 倍生成时间,这是一个显着的结果。
额外的技术细节
Grid生成器 多视角diffusion fintune unet
我们采用在用文本[16]注释的数十亿个图像上预训练的文本到图像扩散模型,并将其输入和输出通道扩展2倍,以支持同时生成阴影外观和反照率。我们微调模型以预测四个图像 I i , i = 1 , … , 4 I_{i}, i=1, \ldots, 4 Ii,i=1,…,4,类似于 [72, 40],通过最小化标准扩散损失。训练总共跨越 2 天,使用 32 个 A100 GPU,总批量大小为 128,学习率为 10e−5
MetaILRM
如主要论文所述,MetaILRM 使用直接 SDF 损失 Lsdf、PBR 损失 Lpbr、延迟阴影损失 Ldef、二元交叉熵损失 Lmask 和深度 MSE 损失 Ldepth 进行优化,因此全局目标是:
L
=
0.5
L
sdf
+
L
pbr
+
0.5
L
def
+
0.1
L
mask
+
0.1
L
depth
.
\mathcal{L}=0.5 \mathcal{L}_{\text {sdf }}+\mathcal{L}_{\text {pbr }}+0.5 \mathcal{L}_{\text {def }}+0.1 \mathcal{L}_{\text {mask }}+0.1 \mathcal{L}_{\text {depth }} .
L=0.5Lsdf +Lpbr +0.5Ldef +0.1Lmask +0.1Ldepth .
纹理细化器仅使用 PBR 损失和延迟着色损失: L p b r + 0.5 L d e f L_{pbr} + 0.5L_{def} Lpbr+0.5Ldef
在每个训练批次中,我们随机抽取每个场景的 4 个视图作为源输入视图 I i I_i Ii 和另外 4 个目标视图 I t g t I_tgt Itgt,其中我们渲染 MetaILRM 预测的 sdf 场,或纹理细化器预测的网格。然后我们评估目标视图中上述损失。每个 GPU 3 个场景随机采样,我们在 64 个 GPUS NVIDIA A100 gpu 上训练,产生 3 × 4 × 64 = 768 张图像的有效批量大小。使用 Adam [39] 优化了总损失,学习率为 10e-4,用于 13K 步。
延迟阴影损失消融
除了定量验证Tab中延迟阴影损失Ldef的好处,如 Tab 1.我们还在图12中提供了定性证明。具体来说,反照率和阴影通道预测的PBR材料在3D灯笼资产的实际金属部分表现出更好的金属度图。
直接SDF损失 L sdf L_\text{sdf} Lsdf
我们遵循Azinovic等人[1]对SDF场的直接SDF监督。给定图像中的像素 p 和对应于像素的光线上的采样点
S
p
S_p
Sp,直接 SDF 损失计算为
L
sdf
(
p
)
=
L
sdf
t
r
(
p
)
+
0.01
L
sdf
f
s
(
p
)
.
\mathcal{L}_{\text {sdf }}(p)=\mathcal{L}_{\text {sdf }}^{\mathrm{tr}}(p)+0.01 \mathcal{L}_{\text {sdf }}^{\mathrm{fs}}(p) .
Lsdf (p)=Lsdf tr(p)+0.01Lsdf fs(p).
L s d f t r L^{tr}_{sdf} Lsdftr 是一个“自由空间”目标,它迫使 MLP 预测位于相机原点和表面截断区域之间的样本 s ∈ S p f s s \in S^{fs}_p s∈Spfs 的值为 1:
L sdf f r ( p ) = 1 ∣ S p f r ∣ ∑ s ∈ S p f s ( D s − 1 ) 2 \mathcal{L}_{\text {sdf }}^{\mathrm{fr}}(p)=\frac{1}{\left|S_{p}^{\mathrm{fr}}\right|} \sum_{s \in S_{p}^{\mathrm{fs}}}\left(D_{s}-1\right)^{2} Lsdf fr(p)= Spfr 1s∈Spfs∑(Ds−1)2
其中 D s D_s Ds是来自MLP的预测SDF。对于截断区域内的样本 ( s ∈ S p t r s \in S^{tr}_p s∈Sptr ),我们应用 L sdf t r L^{tr}_\text{sdf} Lsdftr ,即靠近表面的样本的符号距离目标。
L sdf t r ( p ) = 1 ∣ S p t r ∣ ∑ s ∈ S p t r ( D s − D ^ s ) 2 \mathcal{L}_{\text {sdf }}^{\mathrm{tr}}(p)=\frac{1}{\left|S_{p}^{\mathrm{tr}}\right|} \sum_{s \in S_{p}^{\mathrm{tr}}}\left(D_{s}-\hat{D}_{s}\right)^{2} Lsdf tr(p)= Sptr 1s∈Sptr∑(Ds−D^s)2
由于 B × H × W × N r a y B ×H × W × N_{ray} B×H×W×Nray 点的评估,对此的 NAÏve PyTorch 实现是内存密集型的,其中 B 、 H 、 W 、 N r a y B、H、W、N_{ray} B、H、W、Nray分别是批次中目标图像的数量、高度、宽度和每条射线点的数量。因此,为了支持射线上的大批量、图像分辨率和更密集的点采样,我们使用自定义Triton[65]内核实现了直接的SDF损失。
深度loss L depth \mathcal{L}_{\text {depth}} Ldepth
深度损失 L d e p t h L_depth Ldepth 最小化了渲染深度预测 R d e p t h ( ⋅ ∣ s ^ , π ) R_{depth}(· | \hat{s}, π) Rdepth(⋅∣s^,π)地面真实深度 R d e p t h ( ⋅ ∣ M , π ) R_{depth}(· | M, π) Rdepth(⋅∣M,π)之间的均方误差
L depth = ∥ R depth ( ⋅ ∣ s ^ , π ) − R depth ( ⋅ ∣ M , π ) ∥ 2 \mathcal{L}_{\text {depth }}=\left\|\mathcal{R}_{\text {depth }}(\cdot \mid \hat{s}, \pi)-\mathcal{R}_{\text {depth }}(\cdot \mid M, \pi)\right\|^{2} Ldepth =∥Rdepth (⋅∣s^,π)−Rdepth (⋅∣M,π)∥2
其中 R d e p t h ( s , π ) R_{depth}(s, π) Rdepth(s,π) 是从视点 π 渲染形状表示 s(网格或 SDF)的深度图的算子。
纹理精细化
在第3.3节中描述了我们的纹理细化器的高级概述之后,这里我们提供更多的细节。
如前所述,纹理细化器网络Φ总共接受N + 1个纹理图像Ki。网络的第一个输入是增强纹理图像
K
0
∈
R
V
×
V
×
11
K_0∈R^{V ×V ×11}
K0∈RV×V×11,由下式给出:
∀
v
∈
[
0
,
V
]
2
:
K
0
(
v
)
=
{
k
(
x
v
)
⊕
n
(
x
v
)
⊕
x
v
,
if
v
∈
Im
(
ϕ
)
,
0
,
otherwise
,
where
x
v
=
ϕ
(
v
)
.
\forall v \in[0, V]^{2}: \quad K_{0}(v)=\left\{\begin{array}{ll}k\left(\boldsymbol{x}_{v}\right) \oplus \boldsymbol{n}\left(\boldsymbol{x}_{v}\right) \oplus \boldsymbol{x}_{v}, & \text { if } v \in \operatorname{Im}(\phi), \\\mathbf{0}, & \text { otherwise },\end{array} \text { where } \boldsymbol{x}_{v}=\phi(v) .\right.
∀v∈[0,V]2:K0(v)={k(xv)⊕n(xv)⊕xv,0, if v∈Im(ϕ), otherwise , where xv=ϕ(v).
条件 v ∈ I m ( φ ) v \in I_m(φ) v∈Im(φ)选择与网格点对应的“有效”UV点;⊕表示通道级联,使 K 0 ( v ) K_0(v) K0(v)是来自MetaI LRM、正常 n ( x v ) n(xv) n(xv)和3D点 x v xv xv的5个PBR参数 k ( x v ) k(xv) k(xv)的堆栈。
除了 K 0 K_0 K0,我们输入到网络 Φ 纹理图像 K i K_i Ki,每个图像都是通过直接从相应的输入视图 I i I_i Ii 中查找信息来提取的(因此避开 MetaILRM)。如上所述,每个有效纹理点 v 对应于网格上唯一的 3D 点 xv = φ(v) ∈ M,这反过来又投影到图像 I i I_i Ii 中的像素 u = π i ( x v ) u = π_i(xv) u=πi(xv)。设 χ i ( v ) ∈ 0 , 1 χ_i(v) \in {0, 1} χi(v)∈0,1 是指示点 xv 在图像 I i I_i Ii 中是否可见的标志。当点xv在几个视图中可见时,最好在最正的视图中测量,这是由xv处的法线n与射线方向ωv∝x0−xv之间的余弦相似度ωo·n(xv)捕获的。所有这些信息都是通过设置打包到额外的纹理图像中 K i ∈ R V × V × ( D + 1 ) K_i \in R_V ×V ×(D+1) Ki∈RV×V×(D+1):
∀ v ∈ [ 0 , V ] 2 : K i ( v ) = { I i ( π i ( x v ) ) ⊕ ( ω v ⋅ n ( x v ) ) , if v ∈ Im ( ϕ ) and χ i ( v ) = 1 0 , otherwise \forall v \in[0, V]^{2}: \quad K_{i}(v)=\left\{\begin{array}{ll}I_{i}\left(\pi_{i}\left(\boldsymbol{x}_{v}\right)\right) \oplus\left(\boldsymbol{\omega}_{v} \cdot \boldsymbol{n}\left(\boldsymbol{x}_{v}\right)\right), & \text { if } v \in \operatorname{Im}(\phi) \text { and } \chi_{i}(v)=1 \\\mathbf{0}, & \text { otherwise }\end{array}\right. ∀v∈[0,V]2:Ki(v)={Ii(πi(xv))⊕(ωv⋅n(xv)),0, if v∈Im(ϕ) and χi(v)=1 otherwise
纹理网络Φ是一个U-Net,它以纹理增强纹理图像 K 0 K_0 K0为输入,输出最终的增强纹理 K ∈ R V × V × 5 K∈R_V ×V ×5 K∈RV×V×5。该网络还融合了来自视图特定纹理图像Ki的信息。目标是为每个 UV 点 v 选择 N 个输入视图中的哪一个提供最佳信息。这是通过交叉注意力实现的。具体来说,每个 K i K_i Ki 由另一个 U-Net 并行处理,第一个通过多头交叉注意力查询所有其他信息。在图 13 (a) 中,我们提供了后一个跨视图注意力层的图示。
基于物理的渲染:辐射、BRDFs和模型(重头戏,反复看反复忘)
我们简要总结了辐射测量和标准BRDF模型的关键概念,然后提供了Meta 3D AssetGen中使用的BRDF模型的精确表达式。
辐射
辐射通量 Φ 是流过由单位法线 n 定向的特定表面 A ⊂ R3 的电磁功率。辐射L(p,ω)是p相对于单位正交面积 d A ⊥ dA⊥ dA⊥和单位立体角 d Ω dΩ dΩ的特定方向 ω ω ω的辐射通量密度。单位向量 ω ω ω指向通量传播方向。磁通密度是根据与传播方向正交的区域来衡量的。事实上,通过切割相同“通量管”的所有区域,能量流是相同的;具体区域不相关,而不是辐射的属性。通过考虑与通量方向正交的归一化区域 d A ⊥ dA⊥ dA⊥ 来消除这种依赖关系。
由于辐射以正交区域 d A ⊥ dA⊥ dA⊥为单位表示,为了计算可能不正交的表面斑块 d A dA dA的通量,我们必须考虑缩短因子,该因子将区域 d A dA dA和 d A ⊥ dA⊥ dA⊥联系起来:
d
A
⊥
=
∣
⟨
n
,
ω
⟩
∣
d
A
.
d A_{\perp}=|\langle\boldsymbol{n}, \boldsymbol{\omega}\rangle| d A .
dA⊥=∣⟨n,ω⟩∣dA.
由此,在立体角dΩ中,通过dA向ω方向的通量为
d
Φ
=
L
(
p
,
ω
)
∣
⟨
n
,
ω
⟩
∣
d
A
d
Ω
.
d \Phi=L(p, \boldsymbol{\omega})|\langle\boldsymbol{n}, \boldsymbol{\omega}\rangle| d A d \Omega .
dΦ=L(p,ω)∣⟨n,ω⟩∣dAdΩ.
请注意, d Φ dΦ dΦ 取决于 ω ω ω和 n n n,而 L 仅取决于 ω。这强化了 n 是表面属性而不是辐射的概念。
反射模型
设 p 是表面 A 上的一个点,它将两个media分开,让 dA 是位于 p 处的表面补丁。设 n 是此时的法线。我们现在考虑 A 将空气或空白空间与不透明对象分开的情况,n 表示该对象之外。设ω是曲面的同一侧的方向,即⟨n,ω⟩≥0。从物体的角度看,我们将L(p,ω)解释为出射辐射通量,L(p,−ω)解释为入射辐射通量。这两个量由双向反射分布函数 (BRDF) f 相关,定义如下:
d L ( p , ω o ) d Ω i = f ( p , ω i , ω o ) ⟨ n , ω i ⟩ L ( p , − ω i ) . \frac{d L\left(p, \boldsymbol{\omega}_{\mathrm{o}}\right)}{d \Omega_{\mathrm{i}}}=f\left(p, \boldsymbol{\omega}_{\mathrm{i}}, \boldsymbol{\omega}_{\mathrm{o}}\right)\left\langle\boldsymbol{n}, \boldsymbol{\omega}_{\mathrm{i}}\right\rangle L\left(p,-\boldsymbol{\omega}_{\mathrm{i}}\right) . dΩidL(p,ωo)=f(p,ωi,ωo)⟨n,ωi⟩L(p,−ωi).
在这个定义中,为方便起见,
ω
i
ω_i
ωi 和
ω
o
ω_o
ωo都取自与 n 相同的边(因此 ωi 前面的负符号)。一个有用的结果是我们不需要取内积
⟨
n
,
ω
i
⟩
⟨n,ωi⟩
⟨n,ωi⟩的绝对值,因为这根据定义是正的。因此,BRDF从方向
−
ω
i
−ω_i
−ωi接收辐射,并将其沿各种传出方向
ω
o
ω_o
ωo分布。整合所有传入方向,使用反射到
ω
o
ω_o
ωo 的整体辐射:
L
(
p
,
ω
o
)
=
∫
H
(
n
)
d
L
(
p
,
ω
o
)
d
Ω
i
d
ω
i
=
∫
H
(
n
)
f
(
p
,
ω
i
,
ω
o
)
⟨
n
,
ω
i
⟩
L
(
p
,
−
ω
i
)
d
Ω
i
.
L\left(p, \boldsymbol{\omega}_{\mathrm{o}}\right)=\int_{H(\boldsymbol{n})} \frac{d L\left(p, \boldsymbol{\omega}_{\mathrm{o}}\right)}{d \Omega_{\mathrm{i}}} d \boldsymbol{\omega}_{\mathrm{i}}=\int_{H(\boldsymbol{n})} f\left(p, \boldsymbol{\omega}_{\mathrm{i}}, \boldsymbol{\omega}_{\mathrm{o}}\right)\left\langle\boldsymbol{n}, \boldsymbol{\omega}_{\mathrm{i}}\right\rangle L\left(p,-\boldsymbol{\omega}_{\mathrm{i}}\right) d \Omega_{\mathrm{i}} .
L(p,ωo)=∫H(n)dΩidL(p,ωo)dωi=∫H(n)f(p,ωi,ωo)⟨n,ωi⟩L(p,−ωi)dΩi.
其中 H ( n ) = ω : ⟨ n , ω ⟩ ≥ 0 H(n) = {ω : ⟨n, ω⟩ ≥ 0} H(n)=ω:⟨n,ω⟩≥0 是半球。接下来,我们为 PBR 中的 BRDF 函数提供了常见的基本模型。
Diffuse 反射
在漫反射中,辐射被材料吸收,内部分散在随机方向上,再次输出以产生均匀分布。也就是说,漫反射BRDF是:
f ( p , ω i , ω o ) = R π f\left(p, \boldsymbol{\omega}_{\mathrm{i}}, \boldsymbol{\omega}_{\mathrm{o}}\right)=\frac{R}{\pi} f(p,ωi,ωo)=πR
其中 0 ≤ R ≤ 1 0 ≤ R ≤ 1 0≤R≤1 是扩散过程反映的功率分数。 1 / π 1/π 1/π因子确保当 R = 1 R = 1 R=1 时总能量守恒。
镜面反射Specular reflectance
p 处两个介质之间完美平坦界面的反射是镜面反射的:入射光辐射 -ωi 部分反映在镜面反射方向 ωo = r(n, ωi) = 2n⟨n, ωi⟩ - ωi 和部分传输。这种现象的特点是菲涅耳方程,这些方程来自麦克斯韦方程,利用两个介质界面处电磁场的连续性条件。菲涅耳方程完全描述了平面辐射,包括它的偏振(在最一般的情况下,使用相量,因此复数)。对于图形,我们假设光是非偏振的,所以我们只计算功率。反射的功率分数由菲涅耳系数给出(使用 Schlick 的近似 [70]):
F ( ⟨ n , ω i ⟩ ) = F 0 + ( 1 − F 0 ) ∣ ⟨ n , ω i ⟩ ∣ 5 , F 0 = ( n ^ 1 − n ^ 2 n ^ 1 + n ^ 2 ) 2 . F\left(\left\langle\boldsymbol{n}, \boldsymbol{\omega}_{\mathrm{i}}\right\rangle\right)=F_{0}+\left(1-F_{0}\right)\left|\left\langle\boldsymbol{n}, \boldsymbol{\omega}_{\mathrm{i}}\right\rangle\right|^{5}, \quad F_{0}=\left(\frac{\hat{n}_{1}-\hat{n}_{2}}{\hat{n}_{1}+\hat{n}_{2}}\right)^{2} . F(⟨n,ωi⟩)=F0+(1−F0)∣⟨n,ωi⟩∣5,F0=(n^1+n^2n^1−n^2)2.
这里 n ^ 1 \hat n_1 n^1 和 n ^ 2 \hat n_2 n^2 分别是两个介质的反射率指数。该方程对电介质(非金属物体)有效,但也通过调整 F0 作为金属的近似值。
为了将这种关系写为 BRDF,我们写为:
L ( p , ω o ) = ∫ H ( n ) f ( p , ω i , ω o ) ⟨ n , ω i ⟩ L ( p , − ω i ) d Ω i = R ( ⟨ n , r ( n , ω o ) ⟩ ) L ( p , − r ( n , ω o ) ) . L\left(p, \boldsymbol{\omega}_{\mathrm{o}}\right)=\int_{H(\boldsymbol{n})} f\left(p, \boldsymbol{\omega}_{\mathrm{i}}, \boldsymbol{\omega}_{\mathrm{o}}\right)\left\langle\boldsymbol{n}, \boldsymbol{\omega}_{\mathrm{i}}\right\rangle L\left(p,-\boldsymbol{\omega}_{\mathrm{i}}\right) d \Omega_{\mathrm{i}}=R\left(\left\langle\boldsymbol{n}, r\left(\boldsymbol{n}, \boldsymbol{\omega}_{\mathrm{o}}\right)\right\rangle\right) L\left(p,-r\left(\boldsymbol{n}, \boldsymbol{\omega}_{\mathrm{o}}\right)\right) . L(p,ωo)=∫H(n)f(p,ωi,ωo)⟨n,ωi⟩L(p,−ωi)dΩi=R(⟨n,r(n,ωo)⟩)L(p,−r(n,ωo)).
因此,BRDF必须是以 ω i ∗ = r ( n , ω o ) ω^∗_i=r(n,ω_o) ωi∗=r(n,ωo)为中心的增量函数:
f ( p , ω i , ω o ) = F ( ⟨ n , ω o ⟩ ) ⟨ n , ω o ⟩ δ r ( n , ω o ) ( ω i ) f\left(p, \boldsymbol{\omega}_{\mathrm{i}}, \boldsymbol{\omega}_{\mathrm{o}}\right)=\frac{F\left(\left\langle\boldsymbol{n}, \boldsymbol{\omega}_{\mathrm{o}}\right\rangle\right)}{\left\langle\boldsymbol{n}, \boldsymbol{\omega}_{\mathrm{o}}\right\rangle} \delta_{r\left(n, \boldsymbol{\omega}_{\mathrm{o}}\right)}\left(\boldsymbol{\omega}_{\mathrm{i}}\right) f(p,ωi,ωo)=⟨n,ωo⟩F(⟨n,ωo⟩)δr(n,ωo)(ωi)
其中我们使用了 ⟨ n , r ( n , ω o ) ⟩ = ⟨ n , ω o ⟩ ⟨n,r(n,ω_o)⟩=⟨n,ω_o⟩ ⟨n,r(n,ωo)⟩=⟨n,ωo⟩的事实,其中 δ r ( n , ω o ) δ_r(n,ω_o) δr(n,ωo)是以 r ( n , ω o ) r(n,ω_o) r(n,ωo)为中心的增量分布。
微表面理论
粗糙表面虽然可以作为随机取向的平面微面的集合,每个面以镜面方式反射光。考虑表面和入射辐射方向 ω i ω_i ωi和 ω o ω_o ωo上的点p。如果点包含一个微面,使光从 ω i ω_i ωi反射到 ω o ω_o ωo,那么微面法线必须是 m ∝ ω i + ω o m∝ω_i + ω_o m∝ωi+ωo。如果微面朝其他地方定向,则没有方向 ωo 的光流。因此,我们可以写
m = h ( ω i , ω o ) = ω i + ω o ∣ ω i + ω o ∣ \boldsymbol{m}=h\left(\boldsymbol{\omega}_{\mathrm{i}}, \boldsymbol{\omega}_{\mathrm{o}}\right)=\frac{\boldsymbol{\omega}_{\mathrm{i}}+\boldsymbol{\omega}_{\mathrm{o}}}{\left|\boldsymbol{\omega}_{\mathrm{i}}+\boldsymbol{\omega}_{\mathrm{o}}\right|} m=h(ωi,ωo)=∣ωi+ωo∣ωi+ωo
作为传入辐射和传出辐射的函数。这称为半程向量,因为它位于两个向量 ω i ω_i ωi 和 ω o ω_o ωo 之间。现在我们希望从微观BRDF F (p, ωi, ωo|m)推导出宏观BRDF f ( p , ω i , ω o ) f (p, ω_i, ω_o) f(p,ωi,ωo),其中我们强调了BRDF相对于微面法线m的方向的事实。一个简短的计算[88]表明:
f ( p , ω i , ω o ) = f m ( p , ω i , ω o ∣ m ) ⟨ m , ω i ⟩ ⟨ n , ω i ⟩ ⟨ m , ω o ⟩ ⟨ n , ω o ⟩ 1 ⟨ m , n ⟩ . f\left(p, \boldsymbol{\omega}_{\mathrm{i}}, \boldsymbol{\omega}_{\mathrm{o}}\right)=f_{m}\left(p, \boldsymbol{\omega}_{\mathrm{i}}, \boldsymbol{\omega}_{\mathrm{o}} \mid \boldsymbol{m}\right) \frac{\left\langle\boldsymbol{m}, \boldsymbol{\omega}_{\mathrm{i}}\right\rangle}{\left\langle\boldsymbol{n}, \boldsymbol{\omega}_{\mathrm{i}}\right\rangle} \frac{\left\langle\boldsymbol{m}, \boldsymbol{\omega}_{\mathrm{o}}\right\rangle}{\left\langle\boldsymbol{n}, \boldsymbol{\omega}_{\mathrm{o}}\right\rangle} \frac{1}{\langle\boldsymbol{m}, \boldsymbol{n}\rangle} . f(p,ωi,ωo)=fm(p,ωi,ωo∣m)⟨n,ωi⟩⟨m,ωi⟩⟨n,ωo⟩⟨m,ωo⟩⟨m,n⟩1.
在实践中,可能的表面法线 m 上的分布,其特征是微面分布函数 D ( m ∣ n ) D(m|n) D(m∣n)。后者的定义使得 D ( m ∣ n ) d A d Ω m D(m|n) dA dΩm D(m∣n)dAdΩm为总面积具有 d Ω m dΩm dΩm方向的宏观表面斑块 d A dA dA内的微面。在实践中,只有部分微面可见和照明,这取决于与其他面的相互作用。这由阴影掩蔽函数 G ( ω i , ω o , m , n ) ∈ [ 0 , 1 ] G(ω_i, ω_o, m, n) ∈ [0, 1] G(ωi,ωo,m,n)∈[0,1] 来解释。因此,预期的反射率为:
f ( p , ω i , ω o ) = ∫ H ( n ) ⟨ m , ω i ⟩ ⟨ n , ω i ⟩ ⟨ m , ω o ⟩ ⟨ n , ω o ⟩ f m ( p , ω i , ω o ∣ m ) D ( m ∣ n ) G ( ω i , ω o , m , n ) d Ω m . f\left(p, \boldsymbol{\omega}_{\mathrm{i}}, \boldsymbol{\omega}_{\mathrm{o}}\right)=\int_{H(\boldsymbol{n})} \frac{\left\langle\boldsymbol{m}, \boldsymbol{\omega}_{\mathrm{i}}\right\rangle}{\left\langle\boldsymbol{n}, \boldsymbol{\omega}_{\mathrm{i}}\right\rangle} \frac{\left\langle\boldsymbol{m}, \boldsymbol{\omega}_{\mathrm{o}}\right\rangle}{\left\langle\boldsymbol{n}, \boldsymbol{\omega}_{\mathrm{o}}\right\rangle} f_{m}\left(p, \boldsymbol{\omega}_{\mathrm{i}}, \boldsymbol{\omega}_{\mathrm{o}} \mid \boldsymbol{m}\right) D(\boldsymbol{m} \mid \boldsymbol{n}) G\left(\boldsymbol{\omega}_{\mathrm{i}}, \boldsymbol{\omega}_{\mathrm{o}}, \boldsymbol{m}, \boldsymbol{n}\right) d \Omega_{m} . f(p,ωi,ωo)=∫H(n)⟨n,ωi⟩⟨m,ωi⟩⟨n,ωo⟩⟨m,ωo⟩fm(p,ωi,ωo∣m)D(m∣n)G(ωi,ωo,m,n)dΩm.
将每个微面的镜面反射fm的值代入:
f ( p , ω i , ω o ) = F ( ⟨ h , ω o ⟩ ) D ( h ∣ n ) G ( ω i , ω o , h , n ) 4 ⟨ n , ω i ⟩ ⟨ n , ω o ⟩ where h = h ( ω i , ω o ) . f\left(p, \boldsymbol{\omega}_{\mathrm{i}}, \boldsymbol{\omega}_{\mathrm{o}}\right)=\frac{F\left(\left\langle\boldsymbol{h}, \boldsymbol{\omega}_{\mathrm{o}}\right\rangle\right) D(\boldsymbol{h} \mid \boldsymbol{n}) G\left(\boldsymbol{\omega}_{\mathrm{i}}, \boldsymbol{\omega}_{\mathrm{o}}, \boldsymbol{h}, \boldsymbol{n}\right)}{4\left\langle\boldsymbol{n}, \boldsymbol{\omega}_{\mathrm{i}}\right\rangle\left\langle\boldsymbol{n}, \boldsymbol{\omega}_{\mathrm{o}}\right\rangle} \text { where } \boldsymbol{h}=h\left(\boldsymbol{\omega}_{\mathrm{i}}, \boldsymbol{\omega}_{\mathrm{o}}\right) \text {. } f(p,ωi,ωo)=4⟨n,ωi⟩⟨n,ωo⟩F(⟨h,ωo⟩)D(h∣n)G(ωi,ωo,h,n) where h=h(ωi,ωo).
标准微表面模型
在这里,我们讨论了标准 PBR 模型中函数 D 和 G 的常见选择。
Torrance-Sparow 模型
最古老的模型是由于 Torrance 和 Sparrow [85]。他们简单地假设微面分布函数的高斯模型
D
(
m
∣
n
)
=
b
exp
(
−
α
2
θ
)
,
where
cos
θ
=
⟨
m
,
n
⟩
,
D(\boldsymbol{m} \mid \boldsymbol{n})=b \exp \left(-\alpha^{2} \theta\right), \quad \text { where } \cos \theta=\langle\boldsymbol{m}, \boldsymbol{n}\rangle,
D(m∣n)=bexp(−α2θ), where cosθ=⟨m,n⟩,
b 是一个合适的归一化常数。对于他们选择的阴影掩蔽函数:
G ( ω i , ω o , m , n ) = min { 1 , 2 ⟨ m , n ⟩ ⟨ n , ω i ⟩ ⟨ m , ω i ⟩ , 2 ⟨ m , n ⟩ ⟨ n , ω o ⟩ ⟨ m , ω o ⟩ } G\left(\boldsymbol{\omega}_{\mathrm{i}}, \boldsymbol{\omega}_{\mathrm{o}}, \boldsymbol{m}, \boldsymbol{n}\right)=\min \left\{1, \frac{2\langle\boldsymbol{m}, \boldsymbol{n}\rangle\left\langle\boldsymbol{n}, \boldsymbol{\omega}_{\mathrm{i}}\right\rangle}{\left\langle\boldsymbol{m}, \boldsymbol{\omega}_{\mathrm{i}}\right\rangle}, \frac{2\langle\boldsymbol{m}, \boldsymbol{n}\rangle\left\langle\boldsymbol{n}, \boldsymbol{\omega}_{\mathrm{o}}\right\rangle}{\left\langle\boldsymbol{m}, \boldsymbol{\omega}_{\mathrm{o}}\right\rangle}\right\} G(ωi,ωo,m,n)=min{1,⟨m,ωi⟩2⟨m,n⟩⟨n,ωi⟩,⟨m,ωo⟩2⟨m,n⟩⟨n,ωo⟩}
该函数在微表面的基本几何模型下具有简单的几何推导。
Beckmann-Spizzichino-Smith 模型
Beckmann 和 Spizichino [2] 提出了模型:
D
(
m
∣
n
)
=
1
π
α
2
cos
4
θ
e
−
tan
2
θ
α
2
where
cos
θ
=
⟨
m
,
n
⟩
D(\boldsymbol{m} \mid \boldsymbol{n})=\frac{1}{\pi \alpha^{2} \cos ^{4} \theta} e^{-\frac{\tan ^{2} \theta}{\alpha^{2}}} \quad \text { where } \cos \theta=\langle\boldsymbol{m}, \boldsymbol{n}\rangle
D(m∣n)=πα2cos4θ1e−α2tan2θ where cosθ=⟨m,n⟩
Smith[75]指出阴影掩蔽函数应该来自描述表面微几何的微面分布函数。他们还提出了一个分解模型 G ( ω i , ω o , m , n ) = G 1 ( ω i , n ) G 1 ( ω o , n ) G(ω_i, ω_o, m, n) = G1(ω_i, n)G1(ω_o, n) G(ωi,ωo,m,n)=G1(ωi,n)G1(ωo,n)。对于 Beckmann 的分布,Smith 阴影掩蔽函数由下式给出:
G 1 ( ω , n ) = 2 1 + erf ( a ) + 1 a π e − a 2 where a = 1 α tan θ ω and cos θ ω = ⟨ n , ω ⟩ . ( 13 ) G_{1}(\boldsymbol{\omega}, \boldsymbol{n})=\frac{2}{1+\operatorname{erf}(a)+\frac{1}{a \sqrt{\pi}} e^{-a^{2}}} \quad \text { where } a=\frac{1}{\alpha \tan \theta_{\boldsymbol{\omega}}} \text { and } \cos \theta_{\boldsymbol{\omega}}=\langle\boldsymbol{n}, \boldsymbol{\omega}\rangle \text {. } (13) G1(ω,n)=1+erf(a)+aπ1e−a22 where a=αtanθω1 and cosθω=⟨n,ω⟩. (13)
GGX 模型
GGX 模型是 Beckmann 模型的变体,微面分布和阴影掩蔽函数略有不同
D
(
m
∣
n
)
=
α
2
π
cos
4
θ
(
α
2
+
tan
2
θ
)
2
,
G
1
(
ω
,
n
)
=
2
1
+
1
+
α
2
tan
2
θ
ω
D(\boldsymbol{m} \mid \boldsymbol{n})=\frac{\alpha^{2}}{\pi \cos ^{4} \theta\left(\alpha^{2}+\tan ^{2} \theta\right)^{2}}, \quad G_{1}(\boldsymbol{\omega}, \boldsymbol{n})=\frac{2}{1+\sqrt{1+\alpha^{2} \tan ^{2} \theta_{\boldsymbol{\omega}}}}
D(m∣n)=πcos4θ(α2+tan2θ)2α2,G1(ω,n)=1+1+α2tan2θω2
where
cos
θ
=
⟨
m
,
n
⟩
and
cos
θ
ω
=
⟨
n
,
ω
⟩
.
\text { where } \cos \theta=\langle\boldsymbol{m}, \boldsymbol{n}\rangle \text { and } \cos \theta_{\boldsymbol{\omega}}=\langle\boldsymbol{n}, \boldsymbol{\omega}\rangle \text {. }
where cosθ=⟨m,n⟩ and cosθω=⟨n,ω⟩.
Meta 3D AsetGen 中使用的 BRDF 模型
我们论文中使用的BRDF模型结合了漫反射和GGX BRDF:
f ( ω i , ω o ∣ k ( x ) , n ) = R π + F ( h ∣ n ) D ( h ∣ n ) G 1 ( n , ω i ) G 1 ( n , ω o ) 4 ( n ⋅ ω i ) ( n ⋅ ω o ) . f\left(\boldsymbol{\omega}_{\mathrm{i}}, \boldsymbol{\omega}_{\mathrm{o}} \mid k(\boldsymbol{x}), \boldsymbol{n}\right)=\frac{R}{\pi}+\frac{F(\boldsymbol{h} \mid \boldsymbol{n}) D(\boldsymbol{h} \mid \boldsymbol{n}) G_{1}\left(\boldsymbol{n}, \boldsymbol{\omega}_{\mathrm{i}}\right) G_{1}\left(\boldsymbol{n}, \boldsymbol{\omega}_{\mathrm{o}}\right)}{4\left(\boldsymbol{n} \cdot \boldsymbol{\omega}_{\mathrm{i}}\right)\left(\boldsymbol{n} \cdot \boldsymbol{\omega}_{\mathrm{o}}\right)} . f(ωi,ωo∣k(x),n)=πR+4(n⋅ωi)(n⋅ωo)F(h∣n)D(h∣n)G1(n,ωi)G1(n,ωo).
第一项是扩散分量(Lambertian 反射),其中 R ∈ [ 0 , 1 ] R ∈ [0, 1] R∈[0,1] 是扩散反射的光功率的分数。镜面分量中的第二项,其中F为Schlick对菲涅尔反射定律的近似[70] F ( ω i ∣ n ) = F 0 + ( 1 − F 0 ) ( 1 − n ⋅ ω i ) 5 F (ω_i|n) =F0 +(1−F0)(1−n·ω_i)5 F(ωi∣n)=F0+(1−F0)(1−n⋅ωi)5,其中 F 0 ∈ [ 0 , 1 ] F_0∈[0,1] F0∈[0,1]为正常入射时的菲涅耳系数。单位向量 h ∝ ω i + ω o h ∝ ω_i + ω_o h∝ωi+ωo 是半向量,它是由粗糙材料的微表面(通常不同于但平均到 n)将 ω i ω_i ωi 反射到 ω o ω_o ωo所需的方向。函数 D 和 G1 是微面分布函数和阴影掩蔽函数,由下式给出:
D ( m ∣ n ) = α 2 π ( ( m ⋅ n ) 2 ( α 2 − 1 ) + 1 ) 2 , G 1 ( n , ω ) = 2 ( n ⋅ ω ) n ⋅ ω + ( n ⋅ ω ) 2 ( α 2 − 1 ) + α 2 D(\boldsymbol{m} \mid \boldsymbol{n})=\frac{\alpha^{2}}{\pi\left((\boldsymbol{m} \cdot \boldsymbol{n})^{2}\left(\alpha^{2}-1\right)+1\right)^{2}}, \quad G_{1}(\boldsymbol{n}, \boldsymbol{\omega})=\frac{2(\boldsymbol{n} \cdot \boldsymbol{\omega})}{\boldsymbol{n} \cdot \boldsymbol{\omega}+\sqrt{(\boldsymbol{n} \cdot \boldsymbol{\omega})^{2}\left(\alpha^{2}-1\right)+\alpha^{2}}} D(m∣n)=π((m⋅n)2(α2−1)+1)2α2,G1(n,ω)=n⋅ω+(n⋅ω)2(α2−1)+α22(n⋅ω)
这些与方程式 (13) 相同三角函数在点积方面展开。在该模型中,正常入射 F 0 F_0 F0处的反射率R和反射率为RGB三元组。镜面高光颜色 F 0 F_0 F0 对于电介质约为白色(等于 1),并为金属着色;此外,金属没有漫反射分量(R = 0)。因此,我们引入了参数金属 γ ∈ [ 0 , 1 ] \gamma∈[0,1] γ∈[0,1]和基本颜色 ρ 0 ∈ [ 0 , 1 ] 3 ρ_0∈[0,1]^3 ρ0∈[0,1]3,并定义:
R = ρ 0 ( 1 − γ ) , F 0 = 1 ( 1 − γ ) + ρ 0 γ R=\rho_{0}(1-\gamma), \quad F_{0}=\mathbf{1}(1-\gamma)+\rho_{0} \gamma R=ρ0(1−γ),F0=1(1−γ)+ρ0γ
通过这种方式,反照率被用作漫反射颜色或镜面颜色,这取决于材料是电介质还是金属。在本文中,我们将参数ρ_0反照率称为更好的已知概念;然而,在这个模型中, ρ 0 ρ_0 ρ0只有在 γ = 0 γ = 0 γ=0时才是反照率,即当物体是完美的介质时。
因此,BRDF完全由反照率 ρ 0 ρ_0 ρ0、粗糙度 α α α和金属度 γ γ γ描述,总共五个标量参数。因此,LRM 在每个 3D 点 x 处预测三元组 k ( x ) = ( ρ 0 , γ , α ) k(x) = (ρ_0, γ, α) k(x)=(ρ0,γ,α)。