NOPE: Novel Object Pose Estimation from a Single Image

1. 简介

论文名称：20. NOPE: Novel Object Pose Estimation from a Single Image
发表时间：2023
论文链接：https://export.arxiv.org/pdf/2303.13612v1.pdf
代码链接：https://github.com/nv-nguyen/nope?tab=readme-ov-file
效果演示: https://nv-nguyen.github.io/nope/

2. 问题与贡献

本文的研究对象是3D物体姿态估计。文章介绍了一个名为NOPE的方法，该方法只需要一张新物体的单张图像，就可以预测该物体在新图像中的相对姿态，而无需物体的3D模型和对新物体的训练。这是一个非常具有挑战性的任务，因为与其他方法使用多个视角相比，单个视角只能提供有限的关于物体几何的信息。为了实现这一目标，作者训练了NOPE来预测物体在新视角下的外观，并将这些预测作为带有相应姿态的“模板”。通过将这些模板与新的输入视角进行匹配，可以估计物体相对于初始视角的姿态。作者的方法与传统的新视角合成方法有两个关键的不同之处：首先，作者直接预测视角的判别性嵌入，而不是预测彩色图像；其次，作者通过考虑目标视角下物体所有可能外观的分布来处理新视角合成中的模糊性。通过预测平均视角，作者可以处理新视角预测的模糊性，并且这种方法非常快速和鲁棒，适用于部分遮挡的情况。此外，作者的方法还可以识别由于物体的对称性等原因导致的姿态模糊性，即使我们只有单个视角而没有物体的3D模型。

3. 前置概念与理论（相关工作）

• NeRF
• Diffusion: DreamFusion, SparseFusion, RealFusion …
• 3DiM, Zero-1-to-3,
• Feed-forward networks
• Object pose estimation

4. 方法

4.1 Formalization

给定目标图像 $I_r$ 和 查询图像 $I_q$ ， 我们希望估计 $I_r$ 与 $I_q$ 之间的 motion 为某个离散化的相对位姿 $\Delta R$ 的概率为 $p\left(\Delta R\mid I_r,I_q\right)$ 。我们假设该概率在图像的 embedding space 中的服从正态分布，即：

$$p\left(\Delta R\mid I_r,I_q\right)\sim \mathcal{N}\left({\mathbf{e}}_q|\mathbf{e}({\mathbf{e}}_r,\Delta R),\sum ({\mathbf{e}}_r,\Delta R)\right)\text{\hspace{1em}(1)}$$

其中，

• ${\mathbf{e}}_r$ : $I_r$ 的 embedding，
• ${\mathbf{e}}_q$ : $I_q$ 的 embedding，
• $\mathbf{e}({\mathbf{e}}_r,\Delta R)$ : 正态分布的均值
• $\sum ({\mathbf{e}}_r,\Delta R)$ : 正态分布的协方差

这种方式允许我们处理一个这样的事实，即：给定参考图像，物体从视点 $\Delta R$ 可以有不同的外观。

我们取平均值 $\mathbf{e}({\mathbf{e}}_r,\Delta R)$ 作为姿态 $\Delta R$ 中物体外观在物体可能的 3D 形状上的平均 embedding：

$$\mathbf{e}\left({\mathbf{e}}_r,\Delta R\right)={\int }_{\mathcal{M}}\mathbf{e}(\Delta R,\mathcal{M})p\left(\mathcal{M}\mid {\mathbf{e}}_r\right)d\mathcal{M}\text{\hspace{1em}(2)}$$

其中，

• $\mathcal{M}$ : 测试 object 的 3D mesh
• $\mathbf{e}(\Delta R,\mathcal{M})$ : 同一 object 在位姿 $\Delta R$ 下的图像 embedding

$\mathbf{e}({\mathbf{e}}_{\mathbf{r}},\mathbf{\Delta R})$ 可能看起来很复杂，但 实际上仅使用 L2 loss 就可以很轻松训练出一个深度学习网络来预测 :

$$\sum _{\left({\mathbf{e}}_1,{\mathbf{e}}_2,\Delta R\right)}{\Vert F\left({\mathbf{e}}_r,\Delta R\right)-{\mathbf{e}}_2\Vert }^2\text{\hspace{1em}(3)}$$

其中,

• $F$ : 网络
• $({\mathbf{e}}_1,{\mathbf{e}}_2,\Delta R)$ : 训练数据
• ${\mathbf{e}}_1$ : 训练对象视图的 embedding
• ${\mathbf{e}}_2$ : pose 变化后同一对象视图的 embedding

在训练过程中，给定足够的样本， $F\left({\mathbf{e}}_r,\Delta R\right)$ 会很好的收敛于 $\mathbf{e}({\mathbf{e}}_r,\Delta R)$ 。

4.2 Framework

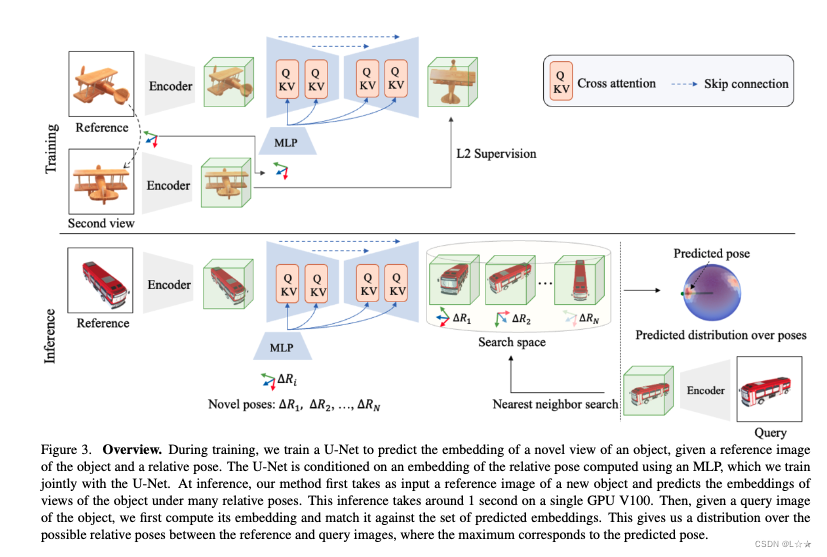
Fig. 3 为网络结构图。

Training:

• 输入：一张目标的图像 $I_q$ ，以及一组训练数据 { ( e 1 , Δ R 1 ) , ⋯   , ( e n , Δ R n ) } \left\{(\mathbf{e}_1, \Delta R_1), \cdots, (\mathbf{e}_n, \Delta R_n)\right\} {(e1​,ΔR1​),⋯,(en​,ΔRn​)} ，其中 ${\mathbf{e}}_i$ 是 $I_q$ 的 embedding， $\Delta R_i$ 是物体相对于 $I_q$ 的姿态。
• loss： 预测图像 embedding 和 查询图像 embedding 的 L2 距离
• VAE： 训练过程中 freeze 掉 VAE 部分

本文工作，在训练阶段没有明确学习任何对称性，但是在 infer 时能够预测姿态的模糊性。

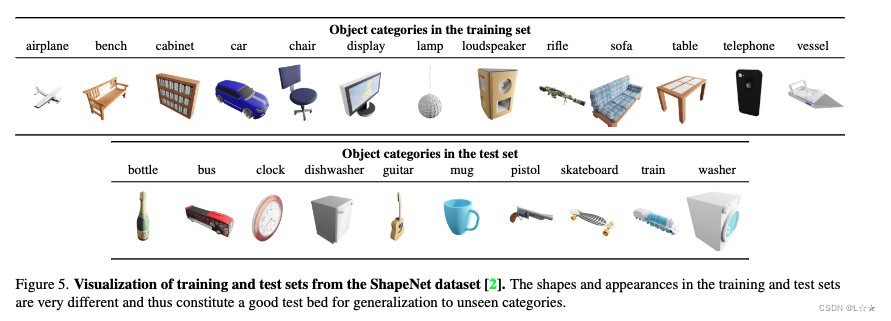
在不同目标的训练集下训练后，模型可以很好的推广到新的未见过的对象类别。

4.3 Pose Prediction

4.3.1 Temmplate matching

给定一张图像 $I_r$ 和 $N$ 个相对视角 $\mathcal{P}=\left(\Delta R_1,\cdots ,\Delta R_N\right)$ , 得到预测的 embedding 集合 $\left({\mathbf{e}}_1,\cdots ,{\mathbf{e}}_N\right)$ 。

视角定义： 从正二十四面体包围框开始，每个三角形拆分为 $4$ 个小三角形， 最终得到 $342$ 个视角。

最后简单的最近临搜索来确定最终pose。

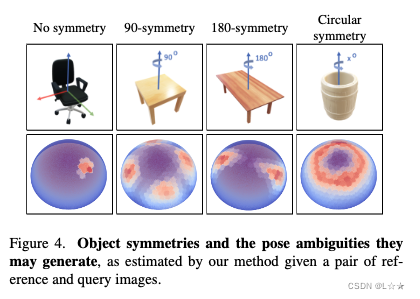
4.3.2 Detecting pose ambiguitities

当目标存在对称性，或者具有辨别意义的特征不可见时，会出现 pose ambiguities 。
通过考虑 查询图像的 embedding 于生成的 embedding 的距离，我们可以得到所有可能的 pose 。

可以简单的在 Eq. (1) 中加入正态分布来表示：

$$\log p\left(\Delta R\mid I_r,I_q\right)\propto {\Vert F\left({\mathbf{e}}_r,\Delta R\right)-{\mathbf{e}}_q\Vert }^2\text{\hspace{1em}(4)}$$

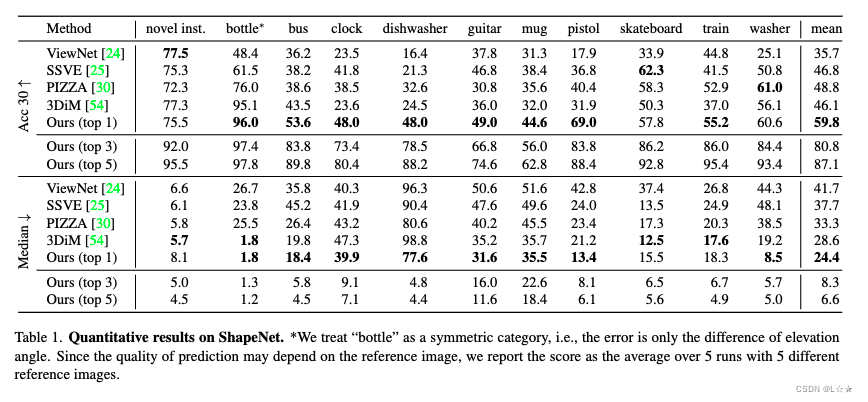
5. 实验

5.1 Dataset

5.2 Qualitative Results

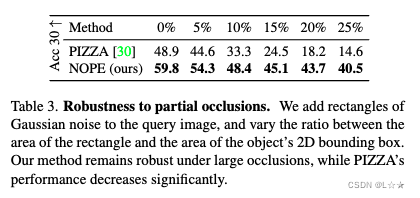
5.3 Robustness to occlusion

5.4 Runtime analysis

7. 总结与思考

本文的主要内容是介绍了一种称为NOPE的方法，可以从单个图像中直接推断出物体的平均视角嵌入，从而准确地估计物体的姿态。该方法不需要重新训练或使用3D模型，即使对于未见过的物体类别也能有效地进行姿态估计，并且能够估计出许多物体姿态的模糊性。 本文的方法有以下优点：

• 直接从单个图像中进行姿态估计，无需额外的训练数据或3D模型。
• 对于未见过的物体类别也能进行准确的姿态估计。
• 能够估计出物体姿态的模糊性。

然而，本文的方法也存在一些不足之处：

• 本文的实验结果可能受到数据集的限制，需要在更多的数据集上进行验证。

总的来说，本文提出的NOPE方法在单个图像中进行物体姿态估计方面取得了较好的结果，但仍需要进一步的研究和实验验证来验证其有效性和泛化性能。