A*(A-star)算法是一种静态网路中求解最短路径最有效的直接搜索算法。在电子游戏中最主要的应用是寻找地图上两点间的最佳路线。在机器人领域中,A*算法常用于移动机器人路径规划。
为了便于理解,本文将以正方形网格地图为例进行讲解。如图,蓝色格子是障碍物,灰色格子是可通过区域,绿色格子是起点(S),红色格子是终点(D)。我们要做的是找到一条从起点到终点的最佳路线。
为了顺利地解决问题,我们先要设定一些约束条件:
1. 从一个格子可以朝周围 8 个方向移动。其中朝上、下、左、右移动的成本为 1,朝左上、右上、左下、右下移动的成本为 1.4(√2 近似值);
2. 不能朝障碍物所在格子移动(显然啦!);
3. 如果右边和上边两个格子都是障碍物,则不能朝右上方的格子移动(如图:不能朝右上和右下两个格子移动,太窄挤不过去呀~)。
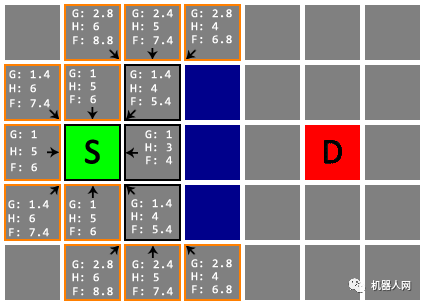
好,下面开始找路!首先,我们把起点 S 加入一个待检查节点的列表(Open List)。接下来,找出 S 周围所有可移动的格子(邻居),算出从 S 移动到该格子的总成本(记为 G),并将 S 设为其父节点。
好,这样我们已经完成了对 S 的检查。把上一步找到的邻居都加入 Open List。从 Open List 中移除 S,并将其加入另一个已检查节点的列表(Closed List)。如图,橙色边框代表待检查节点,黑色边框代表已检查节点。
这下问题来了,Open List 一下有了 8 个待检查节点,先检查哪一个呢?每一个待检查节点都有一个 G 值,代表从起点 S 移动到这个节点的成本。我们再计算出每一个待检查节点与终点 D 之间的曼哈顿距离(只通过朝上、下、左、右四个方向的移动,抵达终点 D 的最短距离。例如,在平面上,坐标(x1, y1)的i点与坐标(x2, y2)的j点的曼哈顿距离为d(i,j)=|x1-x2|+|y1-y2|),作为从该节点移动到终点 D 的估算成本(记为 H)。注意!这里计算曼哈顿距离时要忽略所有障碍物。最后把 G 和 H 相加(记为 F)。
现在,从 Open List 中选出 F 值最小的节点(上图中应该是 S 右边 F 值为 4 的格子),对它执行前面的检查。不过这一次搜索邻居时需要注意以下几点:
1. 如果邻居已经在 Closed List 中,直接忽略;
2. 如果邻居不在 Open List 中,计算 G、H、F,设置父节点,并将其加入 Open List;
3. 这一点非常重要!如果邻居已经在 Open List 中(即该邻居已有父节点),计算从当前节点移动到该邻居是否能使其得到更小的 G 值。如果能,则把该邻居的父节点重设为当前节点,并更新其 G 和 F 值。
完成检查后,把当前节点从 Open List 中移除,放入 Closed List。
继续处理其他待检查节点。
注意!在下面这一次检查中,S 下方两格的节点(星标)更新了 G 值和父节点。
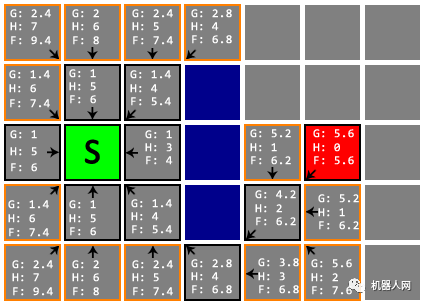
在下面这一步中,我们注意到终点 D 已经进入了 Open List,并且是其中 F 值最小的。
我们从 Open List 取出的 F 值最小的节点后,发现它的 H 值为 0,这意味着我们已经找到了终点 D,搜索到此就可以告一段落。
从终点 D 开始,依次向父节点移动,直到回到起点 S,途经即最佳路线,总长 5.6。
补充几点:
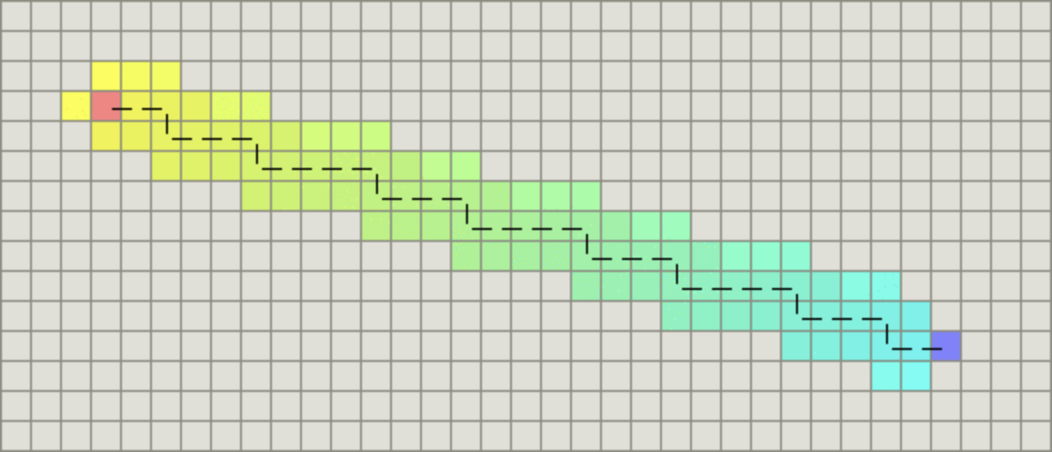
1. 最佳路线可能有多条,比如本文的示例,下图也是一条总长为 5.6 的路线。这取决于当 Open List 存在多个 F 值最小的节点时,先选取哪一个进行搜索;
2. 曼哈顿距离只是估算 H 值最简单的一种方法,常用的方法还有对角距离、欧几里德距离、等。估算方法的优劣是影响算法效率的重要因素;
如果图形中只允许朝上下左右四个方向移动,则启发函数可以使用曼哈顿距离,它的计算方法如下图所示:
对角距离
如果图形中允许斜着朝邻近的节点移动,则启发函数可以使用对角距离。它的计算方法如下:
欧几里得距离
如果图形中允许朝任意方向移动,则可以使用欧几里得距离。
欧几里得距离是指两个节点之间的直线距离,因此其计算方法也是我们比较熟悉的: