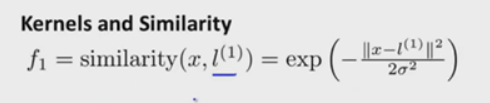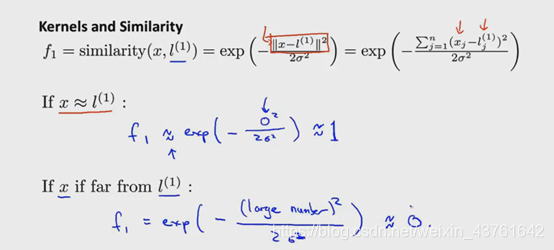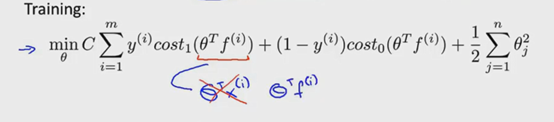核函数
核函数的目的:改造支持向量机来处理非线性问题
如何选择高阶的特征值,哪些高阶的特征值是我们真正需要的
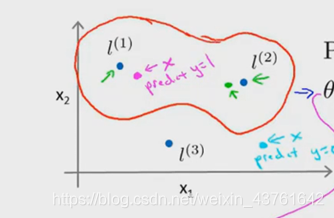
为了方便可视化,我们假定只有两个特征x1,x2
我们手动选择3个点l1,l2,l3
我们想选取新的特征值
于是用下图的相似度函数f1,f2,f3来表示新的特征值,也记做 K(x,l)
计算公式就是下图算是,其中被双竖线框住的是landmark l的欧式距离(也就是两点间的距离)
σ(高斯核函数的参数)
核函数
通过这个函数的计算我们可以得到
当x离landmark很近的时候f=1,表示相似度很高
反之
每个L代表一个新的特征
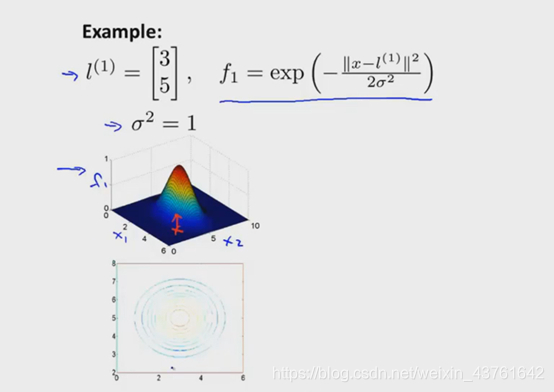
举例,峰顶相似度最高
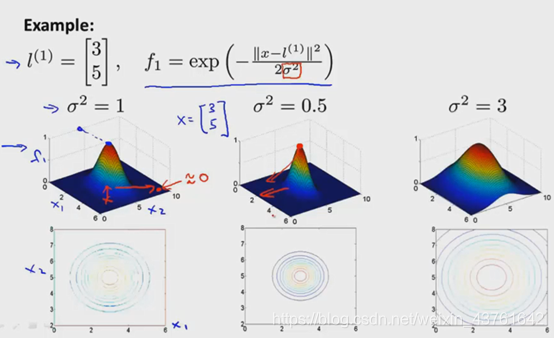
我们可以改变高斯参数 σ观察图像
大了下降的会缓慢,参数越小,峰越陡峭;越大越平缓
来看看采用了新的特征值后我们的假设函数变成了什么样?
给定一个训练样本,下图粉色的点,假设我们已经拟合出参数(途中标注)
当z>=0时,认为预测值为1,下图点经过计算得1
同理可以计算任意给出的点
我们这个模型可以大致得到下图
那么我们怎么得到landmark?
怎么选landmark?
假如我们有m个样本点
我们就把样本点当做landmark
进而算出f1,f2…fm。也就是把所有点都当做landmark
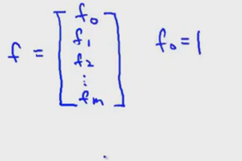
这样我们就得到新的特征向量
同时我们也要把损失函数的x替换为f
这里的n=m
正则化项可以用向量乘积表示