Bootstrap

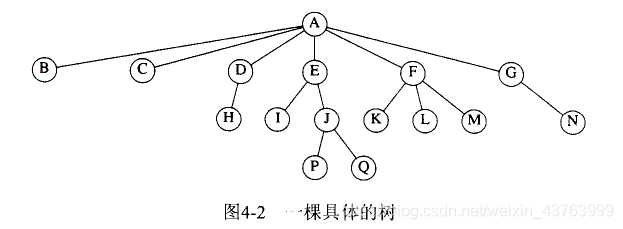
C++数据结构___树

树

数据结构探险之树篇

C++数组实现

tree.h

#program once
#include<bits/stdc++.h>
using namespace std;
class Tree
{
public:
	Tree(int size, int *pRoot);
	~Tree();
	int *SearchNode(int nodeIndex);
	bool AddNode(int nodeIndex, int direction, int *pNode);
	bool DeleteNode(int nodeIndex, int *pNode);
	void TreeTraverse();

private:
	int *m_pTree;
	int m_iSize;
};

tree.cpp

#include "tree.h"
Tree::Tree(int size, int *pRoot)
{
	m_iSize = size;
	m_pTree = new int[size];
	for (int i = 0; i < size; ++i)
	{
		m_pTree[i] = 0;
	}
	m_pTree[0] = *pRoot;
}

Tree::~Tree()
{
	delete[]m_pTree;
	m_pTree = NULL;
}

int *Tree::SearchNode(int nodeIndex)
{
	if (nodeIndex < 0 || nodeIndex >= m_iSize)
	{
		return NULL;
	}
	if (m_pTree[nodeIndex] == 0)
	{
		return NULL;
	}
	return &m_pTree[nodeIndex];
}

bool Tree::AddNode(int nodeIndex, int direction, int *pNode)
{
	if (nodeIndex < 0 || nodeIndex >= m_iSize)
	{
		return false;
	}
	if (m_pTree[nodeIndex] == 0)
	{
		return false;
	}
	if (direction == 0)
	{
		if (nodeIndex * 2 + 1 >= m_iSize)
		{
			return false;
		}
		if (m_pTree[nodeIndex * 2 + 1] != 0)
		{
			return false;
		}

		m_pTree[nodeIndex * 2 + 1] = *pNode;
	}
	if (direction == 1)
	{
		if (nodeIndex * 2 + 2 >= m_iSize)
		{
			return false;
		}
		if (m_pTree[nodeIndex * 2 + 2] != 0)
		{
			return false;
		}

		m_pTree[nodeIndex * 2 + 2] = *pNode;
	}
}

bool Tree::DeleteNode(int nodeIndex, int *pNode)
{
	if (nodeIndex < 0 || nodeIndex >= m_iSize)
	{
		return false;
	}
	if (m_pTree[nodeIndex] == 0)
	{
		return false;
	}
	*pNode = m_pTree[nodeIndex];
	m_pTree[nodeIndex] = 0;
	return true;
}

void Tree::TreeTraverse()
{
	for (int i = 0; i < m_iSize; ++i)
	{
		cout << m_pTree[i] << " ";
	}
}

demo.cpp

#include <iostream>
#include <stdlib.h>
#include "tree.h"
using namespace std;

int main()
{
	int root = 1;
	Tree *pTree = new Tree(10, &root);
	int node1 = 2;
	int node2 = 3;
	int node3 = 4;
	int node4 = 5;
	int node5 = 6;
	int node6 = 7;


	pTree->AddNode(0, 0, &node1);
	pTree->AddNode(0, 1, &node2);
	pTree->AddNode(1, 0, &node3);
	pTree->AddNode(1, 1, &node4);
	pTree->AddNode(2, 0, &node5);
	pTree->AddNode(2, 1, &node6);

	pTree->TreeTraverse();
	int *p = pTree->SearchNode(2);

	cout << endl << "node = " << *p << endl;

	delete pTree;

	return 0;
}

C++链表实现

node.h

#program once
class Node
{
public:
	Node();
	Node *SearchNode(int nodeIndex);
	void DeleteNode();
	void PreoderTraversal();
	void InorderTraversal();
	void PostorderTraversal();
	int index;
	int data;
	Node *pLChild;
	Node *pRChild;
	Node *pParent;
};

node.cpp

#include "Node.h"
#include <stdlib.h>
#include <iostream>
using namespace std;

Node::Node()
{
	index = 0;
	data = 0;
	pLChild = NULL;
	pRChild = NULL;
	pParent = NULL;
}

Node *Node::SearchNode(int nodeIndex)
{
	if (this->index == nodeIndex)
	{
		return this;
	}
	Node *temp = NULL;
	if (this->pLChild != NULL)
	{
		if (this->pLChild->index == nodeIndex)
		{
			return this->pLChild;
		}
		else
		{
			temp = this->pLChild->SearchNode(nodeIndex);
			if (temp != NULL)
			{
				return temp;
			}
		}
	}
	if (this->pRChild != NULL)
	{
		if (this->pRChild->index == nodeIndex)
		{
			return this->pRChild;
		}
		else
		{
			temp = this->pRChild->SearchNode(nodeIndex);
			return temp;
		}
	}

	return NULL;
}

void Node::DeleteNode()
{
	if (this->pLChild != NULL)
	{
		this->pLChild->DeleteNode();
	}
	if (this->pRChild != NULL)
	{
		this->pRChild->DeleteNode();
	}
	if (this->pParent != NULL)
	{
		if (this->pParent->pLChild == this)
		{
			this->pParent->pLChild = NULL;
		}
	}
	if (this->pParent != NULL)
	{
		if (this->pParent->pRChild == this)
		{
			this->pParent->pRChild = NULL;
		}
	}

	delete this;
}

void Node::PreoderTraversal()
{
	cout << this->index << " " << this->data << endl;
	if (this->pLChild != NULL)
	{
		this->pLChild->PreoderTraversal();
	}
	if (this->pRChild != NULL)
	{
		this->pRChild->PreoderTraversal();
	}
}
void Node::InorderTraversal()
{
	if (this->pLChild != NULL)
	{
		this->pLChild->InorderTraversal();
	}
	cout << this->index << " " << this->data << endl;
	if (this->pRChild != NULL)
	{
		this->pRChild->InorderTraversal();
	}
}
void Node::PostorderTraversal()
{
	if (this->pLChild != NULL)
	{
		this->pLChild->PostorderTraversal();
	}
	if (this->pRChild != NULL)
	{
		this->pRChild->PostorderTraversal();
	}
	cout << this->index << " " << this->data << endl;
}

tree.h

#include "Node.h"

class Tree
{
public:
	Tree();
	~Tree();
	Node *SearchNode(int nodeIndex);
	bool AddNode(int nodeIndex, int direction, Node *pNode);
	bool DeleteNode(int nodeIndex, Node *pNode);
	void PreoderTraversal();
	void InorderTraversal();
	void PostorderTraversal();

private:
	Node *m_pRoot;
};

tree.cpp

#include "tree.h"
#include <stdlib.h>

Tree::Tree()
{
	m_pRoot = new Node();
}

Tree::~Tree()
{
	DeleteNode(0, NULL);
	// 	m_pRoot->DeleteNode();
}

Node *Tree::SearchNode(int nodeIndex)
{
	return m_pRoot->SearchNode(nodeIndex);
}

bool Tree::AddNode(int nodeIndex, int direction, Node *pNode)
{
	Node *temp = SearchNode(nodeIndex);
	if (temp == NULL)
	{
		return false;
	}

	Node *node = new Node();
	if (node == NULL)
	{
		return false;
	}
	node->index = pNode->index;
	node->data = pNode->data;
	node->pParent = temp;

	if (direction == 0)
	{
		temp->pLChild = node;
	}
	if (direction == 1)
	{
		temp->pRChild = node;
	}

	return true;
}

bool Tree::DeleteNode(int nodeIndex, Node *pNode)
{
	Node *temp = SearchNode(nodeIndex);
	if (temp == NULL)
	{
		return false;
	}

	if (pNode != NULL)
	{
		pNode->data = temp->data;
	}

	temp->DeleteNode();
	return true;
}

void Tree::PreoderTraversal()
{
	m_pRoot->PreoderTraversal();
}

void Tree::InorderTraversal()
{
	m_pRoot->InorderTraversal();
}

void Tree::PostorderTraversal()
{
	m_pRoot->PostorderTraversal();
}

demo.cpp

#include <iostream>
#include <stdlib.h>
#include "tree.h"
using namespace std;

int main()
{
	Node *node1 = new Node();
	node1->index = 1;
	node1->data = 5;
	Node *node2 = new Node();
	node2->index = 2;
	node2->data = 4;
	Node *node3 = new Node();
	node3->index = 3;
	node3->data = 3;
	Node *node4 = new Node();
	node4->index = 4;
	node4->data = 2;
	Node *node5 = new Node();
	node5->index = 5;
	node5->data = 1;
	Node *node6 = new Node();
	node6->index = 6;
	node6->data = 7;

	Tree *tree = new Tree();
	tree->AddNode(0, 0, node1);
	tree->AddNode(0, 1, node2);
	tree->AddNode(1, 0, node3);
	tree->AddNode(1, 1, node4);
	tree->AddNode(2, 0, node5);
	tree->AddNode(2, 1, node6);

	tree->DeleteNode(6, NULL);
	tree->PostorderTraversal();

	delete tree;

	return 0;
}

二叉树的链式存储结构

typedef struct BiTNode{
	ElemType data;//数据域
	struct BiTNode *lchild, *rchild;//左、右孩子指针
}BiTNode, *BiTree;

二叉树的遍历

例：　1
　　2　　3
　　　4　　5
　　6

先序遍历（PreOrder）

根->左->右

void PreOrder(BiTree T){
	if (T != NULL){
		visit(T);//访问根节点
		PreOrder(T->lchild);//递归遍历左子树
		PreOrder(T->rchild);//递归遍历右子树
	}
}

中序遍历（InOrder）

左->根->右

void InOrder(BiTree T){
	if (T != NULL){
		InOrder(T->lchild);//递归遍历左子树
		visit(T);//访问根节点
		InOrder(T->rchild);//递归遍历右子树
	}
}

后序遍历（PostOrder）

左->右->根

void PostOrder(BiTree T){
	if (T != NULL)
	{
		PostOrder(T->lchild);//递归遍历左子树
		PostOrder(T->rchild);//递归遍历右子树
		visit(T);//访问根节点
	}
}

时间复杂度都是O(n)，空间复杂度为O(n)。

中序遍历的非递归算法

void InOrder2(BiTree T){
	//二叉树中序遍历的非递归算法，算法需要借助一个栈
	InitStack(S);
	BiTree p = T;				//初始化栈；p是遍历指针
	while (p || !IsEmpty(S)){		//栈不空或p不空时循环
		if (p){						//根指针进展，遍历左子树
			Push(S, p);					//每遇到非空二叉树先向左走
			p = p->lchild;
		}
		else{						//根指针退栈，访问根节点，遍历右子树
			Pop(S, p); visit(p);		//退栈，访问根节点
			p = p->rchild;			//再向右子树走
		}
	}
}

二叉树的层次遍历

void LevelOrder(BiTree T){
	InitQueue(Q);//初始化辅助队列
	BiTree p;
	EnQueue(Q, T);//将根结点入队
	while (!IsEmpty(Q)){//队列不空循环
		DeQueue(Q, p);//队头元素出队
		visit(p);//访问当前p所指向结点
		if (p->lchild != NULL)
		{
			EnQueue(Q, p->lchild);//左子树不空，则左子树入队列
		}
		if (p->rchild != NULL)
		{
			EnQueue(Q, p->rchild);//右子树不空，则右子树入队列
		}
	}
}

树的存储结构

双亲表示法

#define MAX_TREE_SIZE 100	//树中最多结点数
typedef struct{		//树的结点定义
	ElemType data;	//数据元素
	int parent;	//双亲位置域
}PTNode;
typedef struct{		//树的类型定义
	PTNode nodes[MAX_TREE_SIZE];	//双亲表示
	int n;		//结点数
}PTree;

求结点的孩子时需遍历整个结构。

孩子表示法

typedef struct CTNode	//孩子结点
{
	int child;
	struct CTNode *next;
}*ChildPtr;
typedef struct
{
	TElemType data;
	ChildPtr firstchild;//孩子链表头指针
}CTBox;
typedef struct
{
	CTBox nodes[MAX_TREE_SIZE];
	int n, r;	//结点数和根的位置
}CTree;

求结点的双亲时需遍历N个结点中孩子链表指针域所指向的N个孩子链表。

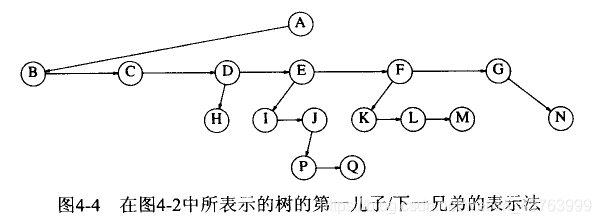
孩子兄弟表示法（二叉树表示法）

typedef struct CSNode
{
	ElemType data;	//数据域
	struct CSNode *firstchild, *nextsibling;	//第一个孩子和右兄弟指针
}CSNode, *CSTree;

易查找结点的孩子，若为每个结点增设一个parent域指向其父节点，则查找结点的父结点也很方便。

树转换为二叉树的规则：每个结点左指针指向它的第一个孩子结点，右指针指向它在树中的相邻兄弟结点，可表示为“左孩子右兄弟”。由于根节点没有兄弟，所以由树转换而得的二叉树没有右子树。

例：
在这里插入图片描述
在这里插入图片描述

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
机器学习笔记（V）线性模型(I)一维最小二乘法
hive在执行任务的时候提示java.io.FileNotFoundException: File does not exist: hdfs://Master:9000/usr/local/apach
【C语言-学生管理系统】
threejs
mybatis-mate 简介
微信小程序连接蓝牙汉印HM-A300L标签打印机
EF4.3 基于代码的迁移演练
《Windows API 每日一练》8.4 edit控件
uni-data-picker修改成自定义样式
Rabbit MQ
;