Bootstrap

C++数据结构——图

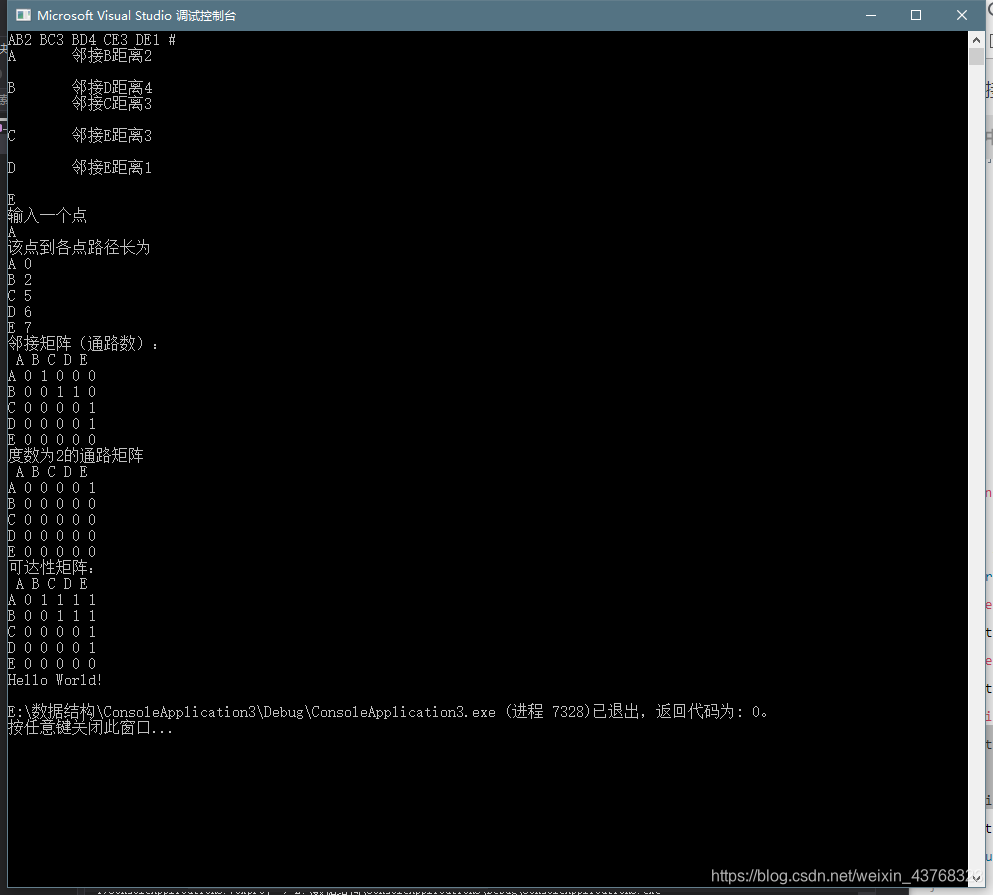
邻接表结构

class sideNode
{
public:
	int weight;
	int datapostion;
	sideNode *next;

};
class pointNode
{
public:
	char data;
	sideNode *head;
};
class map
{
private:
	pointNode pointsArry[max];
	int visited[max];
	int numb;

建立邻接表

map()//初始化
	{
		for (int i = 0; i < max; i++)
		{
			pointsArry[i].data = ' ';
			pointsArry[i].head = NULL;
			visited[i] = 0;
		}
		numb = 0;
	}

	void setPoint()//单独设置点（不带参）
	{
		char t;
		for (int i = 0;;)
		{
			cin >> t;
			if (t == '#')return;
			pointsArry[i].data=t;
			numb++;
			i++;
		}
	}
	void setPoint(char n)//单独设置点（带参数）
	{
		for (int i = 0; i < max; i++)
		{
			if (n == pointsArry[i].data)
				return;
		}
		for (int i = 0;;)
		{
			if (pointsArry[i].data == ' ')
			{
				pointsArry[i].data = n;
				numb++;
				return;
			}
			i++;
		}
	}
	void setSide()//单独设置边
	{
		int w;
		char p1, p2;
		sideNode *p;
		for (;;)
		{
			cin >> p1;
			if (p1 == '#')return;
			cin >> p2;
			cin >> w;
			p = new sideNode;
			p->datapostion = postion(p2);
			p->weight = w;
			p->next = pointsArry[postion(p1)].head;
			pointsArry[postion(p1)].head = p;
		}
	}

	int postion(char m)//返回m在点数组中的位置
	{
		for (int i = 0;; i++)
		{
			if (m == pointsArry[i].data)
				return i;
		}
	}
	void setMapWithWeight()//单向带权重
	{
		int w;
		char p1, p2;
		sideNode *p;
		for (;;)
		{
			cin >> p1;
			if (p1 == '#')return;
			cin >> p2;
			setPoint(p1);
			setPoint(p2);
			cin >> w;
			p = new sideNode;
			p->datapostion = postion(p2);
			p->weight = w;
			p->next = pointsArry[postion(p1)].head;
			pointsArry[postion(p1)].head = p;
		}
	}
	void setMapWithoutWeight()//单向权重默认为1
	{
		char p1, p2;
		sideNode *p;
		for (;;)
		{
			cin >> p1;
			if (p1 == '#')return;
			cin >> p2;
			setPoint(p1);
			setPoint(p2);
			p = new sideNode;
			p->datapostion = postion(p2);
			p->weight = 1;
			p->next = pointsArry[postion(p1)].head;
			pointsArry[postion(p1)].head = p;
		}
	}

生成邻接矩阵

vector<vector<int> >aM()//返回邻接矩阵
	{
		sideNode *u;
		vector<vector<int> >aM(numb, vector<int>(numb));	//邻接矩阵
		for (int i = 0; i < numb; i++)//初始化
		{
			for (int j = 0; j < numb; j++)
			{
				aM[i][j] = 0;
			}
		}
		for (int i = 0; i < numb; i++)//向邻接矩阵中添加通路（不带权）
		{
			
			u = pointsArry[i].head;
			while (u != NULL)
			{
				aM[i][u->datapostion]++;
				u = u->next;
			}
		}
		return aM;
	}

计算可达性矩阵

vector<vector<int> >B(int m)//返回度数为m的通路矩阵
	{
		vector<vector<int> >b(numb, vector<int>(numb));		//各度数的通路矩阵
		vector<vector<int> >T(numb, vector<int>(numb));

		for (int i = 0; i < numb; i++)//初始化
		{
			for (int j = 0; j < numb; j++)
			{
				b[i][j] = 0;
				T[i][j] = 0;
			}
		}
		for (int i = 0; i < numb; i++)
		{
			for (int j = 0; j < numb; j++)
			{
				b[i][j] = aM()[i][j];//此时b为度数为1的通路矩阵
			}
		}
		for (int x = 0; x < m; x++)//循环一次度数加1  ；p=aM^1+aM^2+aM^3+……+aM^(numb-1)
		{
			for (int i = 0; i < numb; i++)//矩阵乘法
			{
				int t, s = 0;
				for (int j = 0; j < numb; j++)
				{
					for (int k = 0; k < numb; k++)
					{
						t = b[i][k] * aM()[k][j];
						s = s + t;
					}
					if (s != 0)s = 1;
					T[i][j] = s;
					s = 0;
				}
			}
			for (int i = 0; i < numb; i++)
			{
				for (int j = 0; j < numb; j++)
				{
					b[i][j] = T[i][j];
				}
			}
		}
		return b;
	}
	vector<vector<int>> P()//返回可达性矩阵
	{
		
		vector<vector<int> >p(numb, vector<int>(numb));		//可达性矩阵
		vector<vector<int> >b(numb, vector<int>(numb));		//各度数的通路矩阵
		vector<vector<int> >T(numb, vector<int>(numb));		

		for (int i = 0; i < numb; i++)//初始化
		{
			for (int j = 0; j < numb; j++)
			{
				p[i][j] = 0;
				b[i][j] = 0;
				T[i][j] = 0;
			}
		}
		for (int i = 0; i < numb; i++)
		{
			for (int j = 0; j < numb; j++)
			{
				b[i][j] = aM()[i][j];//此时b为度数为1的通路矩阵
				p[i][j] = aM()[i][j];
			}
		}
		for (int x=0;x<numb-1;x++)//计算可达性矩阵p；循环一次度数加1  ；p=aM^1+aM^2+aM^3+……+aM^(numb-1)
		{
			for (int i = 0; i < numb; i++)//矩阵乘法
			{
				int t, s = 0;
				for (int j = 0; j < numb; j++)
				{
					for (int k = 0; k < numb; k++)
					{
						t = b[i][k] * aM()[k][j];
						s = s + t;
					}
					if(s!=0)s=1;
					T[i][j] = s;
					s = 0;
				}
			}
			for (int i = 0; i < numb; i++)
			{
				for (int j = 0; j < numb; j++)
				{
					b[i][j] = T[i][j];
				}
			}
			for (int i = 0; i < numb; i++)//相加
			{
				for (int j = 0; j < numb; j++)
				{
					p[i][j] = p[i][j] + b[i][j];
					if (p[i][j] != 0)
					{
						p[i][j] = 1;
					}
				}
			}
		}
		return p;
	}

实现dijkstra算法

int min(int a, int b)
	{
		if (a > b)
			return b;
		else
			return a;
	}
	sideNode* minl(sideNode *p)//返回长度最短的边
	{
		int min;
		sideNode *b = NULL;
		b = p;
		min = p->weight;
		while (p != NULL)
		{
			if (p->weight < min)
			{
				min = p->weight;
				b = p;
			}
			p = p->next;
		}
		return b;
	}
	int minm(int *a)//返回到原点路径长最短的点在数组中的位置
	{
		int min = UN;
		int t = 0;
		for (int i = 0; i < numb; i++)
		{
			if (a[i] < min&&visited[i] != 1)
			{
				min = a[i];
				t = i;
			}

		}
		return t;
	}
	void dij(char t)
	{
		sideNode *temp1, *temp2, *temp3;
		temp1 = pointsArry[postion(t)].head;
		temp2 = pointsArry[minl(temp1)->datapostion].head;
		temp3 = temp2;
		int *m = new int[numb];//最短路径长数组
		int l = minl(pointsArry[postion(t)].head)->weight;//l初始值为距离原点最近的点到原点的路径长
		for (int i = 0; i < numb; i++)//初始化最短路径长数组设2048为不可达
		{
			m[i] = UN;
		}
		m[postion(t)] = 0;//t点到自身长度为0
		visited[postion(t)] = 1;//t点到自身最短路径已知
		while (temp1 != NULL)
		{
			m[temp1->datapostion] = temp1->weight;//更新最短长度数组
			temp1 = temp1->next;
		}
		visited[minl(pointsArry[postion(t)].head)->datapostion] = 1;//标记此端点已得到最短路径长
		for (;;)
		{
			int s = 0;
			for (int i = 0; i < numb; i++)
			{
				s = s + visited[i];
			}
			if (s == numb)break;//全部标记为最短后结束循环
			while (temp3 != NULL)
			{
				m[temp3->datapostion] = min(m[temp3->datapostion], l + temp3->weight);//更新最短路径长数组，
				temp3 = temp3->next;
			}
			l = m[minm(m)];//取到原点路径长最短的
			int y = minm(m);//记此端点在端点数组的位置
			visited[minm(m)] = 1;//标记此端点已得到最短路径长
			temp2 = pointsArry[y].head;//以该端点为起点再次查找
			temp3 = temp2;
		}
		cout << "该点到各点路径长为" << endl;
		for (int i = 0; i < numb; i++)
		{
			cout << pointsArry[i].data << " " << m[i] << endl;
		}
	}

完整代码

#include "pch.h"
#include <iostream>
#include<vector>
#define max 30
#define UN 1024
using namespace std;
class sideNode
{
public:
	int weight;
	int datapostion;
	sideNode *next;

};
class pointNode
{
public:
	char data;
	sideNode *head;
};
class map
{
private:
	pointNode pointsArry[max];
	int visited[max];
	int numb;
public:
	map()//初始化
	{
		for (int i = 0; i < max; i++)
		{
			pointsArry[i].data = ' ';
			pointsArry[i].head = NULL;
			visited[i] = 0;
		}
		numb = 0;
	}

	void setPoint()//单独设置点（不带参）
	{
		char t;
		for (int i = 0;;)
		{
			cin >> t;
			if (t == '#')return;
			pointsArry[i].data=t;
			numb++;
			i++;
		}
	}
	void setPoint(char n)//单独设置点（带参数）
	{
		for (int i = 0; i < max; i++)
		{
			if (n == pointsArry[i].data)
				return;
		}
		for (int i = 0;;)
		{
			if (pointsArry[i].data == ' ')
			{
				pointsArry[i].data = n;
				numb++;
				return;
			}
			i++;
		}
	}
	void setSide()//单独设置边
	{
		int w;
		char p1, p2;
		sideNode *p;
		for (;;)
		{
			cin >> p1;
			if (p1 == '#')return;
			cin >> p2;
			cin >> w;
			p = new sideNode;
			p->datapostion = postion(p2);
			p->weight = w;
			p->next = pointsArry[postion(p1)].head;
			pointsArry[postion(p1)].head = p;
		}
	}

	int postion(char m)//返回m在点数组中的位置
	{
		for (int i = 0;; i++)
		{
			if (m == pointsArry[i].data)
				return i;
		}
	}
	void setMapWithWeight()//单向带权重
	{
		int w;
		char p1, p2;
		sideNode *p;
		for (;;)
		{
			cin >> p1;
			if (p1 == '#')return;
			cin >> p2;
			setPoint(p1);
			setPoint(p2);
			cin >> w;
			p = new sideNode;
			p->datapostion = postion(p2);
			p->weight = w;
			p->next = pointsArry[postion(p1)].head;
			pointsArry[postion(p1)].head = p;
		}
	}
	void setMapWithoutWeight()//单向权重默认为1
	{
		char p1, p2;
		sideNode *p;
		for (;;)
		{
			cin >> p1;
			if (p1 == '#')return;
			cin >> p2;
			setPoint(p1);
			setPoint(p2);
			p = new sideNode;
			p->datapostion = postion(p2);
			p->weight = 1;
			p->next = pointsArry[postion(p1)].head;
			pointsArry[postion(p1)].head = p;
		}
	}
	int min(int a, int b)
	{
		if (a > b)
			return b;
		else
			return a;
	}
	sideNode* minl(sideNode *p)//返回长度最短的边
	{
		int min;
		sideNode *b = NULL;
		b = p;
		min = p->weight;
		while (p != NULL)
		{
			if (p->weight < min)
			{
				min = p->weight;
				b = p;
			}
			p = p->next;
		}
		return b;
	}
	int minm(int *a)//返回到原点路径长最短的点在数组中的位置
	{
		int min = UN;
		int t = 0;
		for (int i = 0; i < numb; i++)
		{
			if (a[i] < min&&visited[i] != 1)
			{
				min = a[i];
				t = i;
			}

		}
		return t;
	}
	void dij(char t)
	{
		sideNode *temp1, *temp2, *temp3;
		temp1 = pointsArry[postion(t)].head;
		temp2 = pointsArry[minl(temp1)->datapostion].head;
		temp3 = temp2;
		int *m = new int[numb];//最短路径长数组
		int l = minl(pointsArry[postion(t)].head)->weight;//l初始值为距离原点最近的点到原点的路径长
		for (int i = 0; i < numb; i++)//初始化最短路径长数组设2048为不可达
		{
			m[i] = UN;
		}
		m[postion(t)] = 0;//t点到自身长度为0
		visited[postion(t)] = 1;//t点到自身最短路径已知
		while (temp1 != NULL)
		{
			m[temp1->datapostion] = temp1->weight;//更新最短长度数组
			temp1 = temp1->next;
		}
		visited[minl(pointsArry[postion(t)].head)->datapostion] = 1;//标记此端点已得到最短路径长
		for (;;)
		{
			int s = 0;
			for (int i = 0; i < numb; i++)
			{
				s = s + visited[i];
			}
			if (s == numb)break;//全部标记为最短后结束循环
			while (temp3 != NULL)
			{
				m[temp3->datapostion] = min(m[temp3->datapostion], l + temp3->weight);//更新最短路径长数组，
				temp3 = temp3->next;
			}
			l = m[minm(m)];//取到原点路径长最短的
			int y = minm(m);//记此端点在端点数组的位置
			visited[minm(m)] = 1;//标记此端点已得到最短路径长
			temp2 = pointsArry[y].head;//以该端点为起点再次查找
			temp3 = temp2;
		}
		cout << "该点到各点路径长为" << endl;
		for (int i = 0; i < numb; i++)
		{
			cout << pointsArry[i].data << " " << m[i] << endl;
		}
	}
	vector<vector<int> >aM()//返回邻接矩阵
	{
		sideNode *u;
		vector<vector<int> >aM(numb, vector<int>(numb));	//邻接矩阵
		for (int i = 0; i < numb; i++)//初始化
		{
			for (int j = 0; j < numb; j++)
			{
				aM[i][j] = 0;
			}
		}
		for (int i = 0; i < numb; i++)//向邻接矩阵中添加通路（不带权）
		{
			
			u = pointsArry[i].head;
			while (u != NULL)
			{
				aM[i][u->datapostion]++;
				u = u->next;
			}
		}
		return aM;
	}
	vector<vector<int> >B(int m)//返回度数为m的通路矩阵
	{
		vector<vector<int> >b(numb, vector<int>(numb));		//各度数的通路矩阵
		vector<vector<int> >T(numb, vector<int>(numb));

		for (int i = 0; i < numb; i++)//初始化
		{
			for (int j = 0; j < numb; j++)
			{
				b[i][j] = 0;
				T[i][j] = 0;
			}
		}
		for (int i = 0; i < numb; i++)
		{
			for (int j = 0; j < numb; j++)
			{
				b[i][j] = aM()[i][j];//此时b为度数为1的通路矩阵
			}
		}
		for (int x = 0; x < m; x++)//循环一次度数加1  ；p=aM^1+aM^2+aM^3+……+aM^(numb-1)
		{
			for (int i = 0; i < numb; i++)//矩阵乘法
			{
				int t, s = 0;
				for (int j = 0; j < numb; j++)
				{
					for (int k = 0; k < numb; k++)
					{
						t = b[i][k] * aM()[k][j];
						s = s + t;
					}
					if (s != 0)s = 1;
					T[i][j] = s;
					s = 0;
				}
			}
			for (int i = 0; i < numb; i++)
			{
				for (int j = 0; j < numb; j++)
				{
					b[i][j] = T[i][j];
				}
			}
		}
		return b;
	}
	vector<vector<int>> P()//返回可达性矩阵
	{
		
		vector<vector<int> >p(numb, vector<int>(numb));		//可达性矩阵
		vector<vector<int> >b(numb, vector<int>(numb));		//各度数的通路矩阵
		vector<vector<int> >T(numb, vector<int>(numb));		

		for (int i = 0; i < numb; i++)//初始化
		{
			for (int j = 0; j < numb; j++)
			{
				p[i][j] = 0;
				b[i][j] = 0;
				T[i][j] = 0;
			}
		}
		for (int i = 0; i < numb; i++)
		{
			for (int j = 0; j < numb; j++)
			{
				b[i][j] = aM()[i][j];//此时b为度数为1的通路矩阵
				p[i][j] = aM()[i][j];
			}
		}
		for (int x=0;x<numb-1;x++)//计算可达性矩阵p；循环一次度数加1  ；p=aM^1+aM^2+aM^3+……+aM^(numb-1)
		{
			for (int i = 0; i < numb; i++)//矩阵乘法
			{
				int t, s = 0;
				for (int j = 0; j < numb; j++)
				{
					for (int k = 0; k < numb; k++)
					{
						t = b[i][k] * aM()[k][j];
						s = s + t;
					}
					if(s!=0)s=1;
					T[i][j] = s;
					s = 0;
				}
			}
			for (int i = 0; i < numb; i++)
			{
				for (int j = 0; j < numb; j++)
				{
					b[i][j] = T[i][j];
				}
			}
			for (int i = 0; i < numb; i++)//相加
			{
				for (int j = 0; j < numb; j++)
				{
					p[i][j] = p[i][j] + b[i][j];
					if (p[i][j] != 0)
					{
						p[i][j] = 1;
					}
				}
			}
		}
		return p;
	}
	void visitTable()//打印邻接表
	{
		sideNode *u;
		int i = 0;
		for (i = 0; i < numb; i++)
		{
			u = pointsArry[i].head;

			cout << pointsArry[i].data << "	";
			while (u != NULL)
			{
				cout << "邻接" << pointsArry[u->datapostion].data << "距离" << u->weight << endl << "	";
				u = u->next;
			}
			cout << endl;
		}
	}
	void visitMatrix(vector<vector<int>> m)//打印矩阵
	{
		cout << " ";
		for (int i = 0; i < numb; i++)
		{
			cout << pointsArry[i].data <<" " ;
		}
		cout << endl;
		for (int i = 0; i < numb; i++)
		{
			cout << pointsArry[i].data << " " ;
			for (int j = 0; j < numb; j++)
			{
				cout << m[i][j] << " ";
			}
			cout << endl;
		}
	}
};

int main()
{
	map a;
	char x;
	a.setMapWithWeight();
	a.visitTable();
	cout << "输入一个点" << endl;
	cin >> x;
	a.dij(x);
	cout << "邻接矩阵（通路数）：" << endl;
	a.visitMatrix(a.aM());
	cout << "度数为2的通路矩阵" << endl;
	a.visitMatrix(a.B(2));
	cout << "可达性矩阵：" << endl;
	a.visitMatrix(a.P());
    std::cout << "Hello World!\n"; 
}

测试

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
【前端速通系列|第二篇】Vue3前置知识
java springboot中@OneToMany、@ManyToOne以及@ManyToMany讲解
京东 | AI人才联合培养计划（NLP项目实战）
apache-kafka-3.2.0k之kRaft模式集群安装
SAP WM 确定WM移动类型配置里'存储地点参考'优先级高于'特殊移动标记'
Unity excle 配置 ScriptObject脚本资源 excel转SO 学习笔记
Open Cv Matrix 详解
Flink中的数据倾斜与解决方案实践
深入理解CSS溢出overflow
python3 asyncio loop 使用线程池原理
;