Semantics-Guided Neural Networks for Efficient Skeleton-Based Human Action Recognition

2020 CVPR | code | PDF | modified code

Abstract

由于人体骨骼数据易于获取，基于骨骼的人体动作识别引起了极大的兴趣。最近，有一种趋势是使用非常深的前馈神经网络对关节的 3D 坐标进行建模，而不考虑计算效率。在这项工作中，我们提出了一个简单而有效的语义引导神经网络（SGN）。我们显式地将关节的高级语义（关节类型和帧索引）引入网络以增强特征表示能力。此外，我们通过两个模块来层次化地利用关节之间的关系，即关节级别模块和框架级别模块，前者（joint-level module）用于建模同一帧中关节的相关性，后者（frame-level module）用于将同一帧中的关节作为一个整体来建模帧之间的依赖关系。提出了一个强有力的基线，以促进这一领域的研究。与大多数以前的工作相比，SGN的模型尺寸小了一个数量级，在NTU60、NTU120和SYSU数据集上实现了最先进的性能。Skeleton-based human action recognition has attracted great interest thanks to the easy accessibility of the human skeleton data. Recently, there is a trend of using very deep feedforward neural networks to model the 3D coordinates of joints without considering the computational efficiency. In this paper, we propose a simple yet effective semantics-guided neural network (SGN) for skeleton-based action recognition. We explicitly introduce the high level semantics of joints (joint type and frame index) into the network to enhance the feature representation capability. In addition, we exploit the relationship of joints hierarchically through two modules, i.e., a joint-level module for modeling the correlations of joints in the same frame and a frame-level module for modeling the dependencies of frames by taking the joints in the same frame as a whole. A strong baseline is proposed to facilitate the study of this field. With an order of magnitude smaller model size than most previous works, SGN achieves the state-of-the-art performance on the NTU60, NTU120, and SYSU datasets.

1. Introduction

人体行为识别有着广泛的应用场景，如人机交互和视频检索。近年来，基于骨骼的动作识别受到越来越多的关注。骨架是一种结构良好的数据类型，人体的每个关节都由关节类型、帧索引和3D位置标识。使用骨架进行动作识别有几个优点。首先，骨架是人体的高级表示，抽象了人体姿势和运动。在生物学上，即使没有外观信息，人类也能够通过仅观察关节的运动来识别动作类别。其次，具有成本效益的深度相机和姿态估计技术的进步使骨骼的访问变得更加容易。第三，与 RGB 视频相比，骨架表示对视点和外观的变化具有鲁棒性。第四，由于低维表示，它在计算上也是有效的。此外，基于骨架的动作识别也是基于 RGB 的动作识别的补充。在这项工作中，我们专注于基于骨架的动作识别。Human action recognition has a wide range of application scenarios, such as human-computer interaction and video retrieval. In recent years, skeleton-based action recognition is attracting increasing interests. Skeleton is a type of well structured data with each joint of the human body identified by a joint type, a frame index, and a 3D position. There are several advantages of using the skeleton for action recognition. First, skeleton is a high level representation of the human body with the human pose and motion abstracted. Biologically, human is able to recognize the action category by observing only the motion of joints even without appearance information. Second, the advance of cost effective depth cameras and pose estimation technology make the access of skeleton much easier. Third, compared with RGB video, the skeleton representation is robust to variation of viewpoint and appearance. Fourth, it is also computationally efficient because of low dimensional representation. Besides, skeleton-based action recognition is also complementary to the RGB-based action recognition. In this work, we focus on skeleton-based action recognition.

对于基于骨架的动作识别，深度学习被广泛用于对骨架序列的时空演化进行建模，目前已经有了各种网络结构，例如循环神经网络（RNN）、卷积神经网络（CNN）和图卷积网络（ GCN）。在早期，RNN/LSTM 是用于开发短期和长期时间动态的首选网络。最近，有一种趋势是使用前馈（即非循环）卷积神经网络对语音、语言和骨架中的序列进行建模，因为它们具有卓越的性能。大多数基于骨架的方法将关节的坐标组织到 2D 映射中，并将映射的大小调整为适合 CNN 输入（例如 ResNet50）的大小（例如 224×224）。它的行/列对应于不同类型的关节/框架索引。在这些方法中，长期依赖和语义信息有望被深度网络的大感受野捕获。但这些方法通常会导致模型复杂度高。For skeleton-based action recognition, deep learning is widely used to model the spatio-temporal evolution of the skeleton sequenceVarious network structures have been exploited, such as Recurrent Neural Networks (RNN), Convolutional Neural Networks (CNN), and Graph Convolutional Networks (GCN). In the early years, RNN/LSTM was the favored network to be used to exploit the short and long term temporal dynamics. Recently, there is a trend of using feedforward (i.e., non-recurrent) convolutional neural networks for modeling sequences in speech, language, and skeleton due to their superior performance. Most skeleton-based approaches organize the coordinates of joints to a 2D map and resize the map to a size (e.g. 224×224) suitable for the input of a CNN (e.g. ResNet50). Its rows/columns correspond to the different types of joints/frames indexes. In these methods, long-term dependencies and semantic information are expected to be captured by the large receptive fields of deep networks. This appears to be brutal and typically results in high model complexity.

直观地说，语义信息，即关节类型和帧索引，对于动作识别非常重要。语义与动力学（如 3D 坐标）一起揭示了人体关节的空间和时间配置/结构。众所周知，具有相同坐标但语义不同的两个关节会传递非常不同的信息。比如头顶的一个关节，如果这个关节是手关节，那么动作很可能是举手；如果是脚关节，动作可能是踢腿。此外，时间信息对于动作识别也很重要。以坐下和起身这两个动作为例，它们的区别仅在于帧的出现顺序。然而，大多数方法都忽略了语义信息的重要性并没有充分探索它。Intuitively, semantic information, i.e., the joint type and the frame index, is very important for action recognition. Semantics together with dynamics (i.e., 3D coordinates) reveal the spatial and temporal configuration/structure of human body joints. As we know, two joints of the same coordinates but different semantics would deliver very different information. For example, for a joint above the head, if this joint is a hand joint, the action is likely to be raising hand; if it is a foot joint, the action may be kicking a leg. Besides, the temporal information is also important for action recognition. Taking the two actions of sitting down and standing up as examples, they are different only in occurrence order of the frames. However, most approaches overlook the importance of the semantic information and underexplore it.

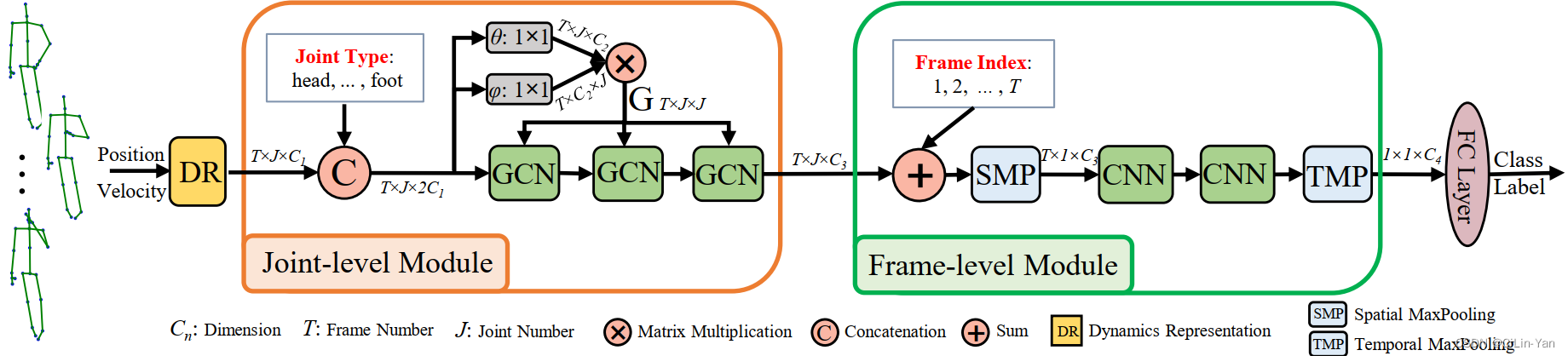
为了解决当前方法的上述局限性，我们提出了一种语义引导的神经网络（SGN），它明确地利用语义和动力学来进行高效的基于骨架的动作识别。图 2 显示了整体框架。我们通过顺序探索骨架序列的关节级和帧级依赖关系来构建分层网络。为了更好的关节级相关建模，除了动力学之外，我们将关节类型（例如，“头部”和“臀部”）的语义合并到 GCN 层中，从而实现内容自适应图的构建和每个关节之间的有效消息传递框架。为了更好的帧级相关建模，我们将时间帧索引的语义结合到网络中。特别是，我们对同一帧内关节的所有特征执行 Spatial MaxPooling (SMP) 操作，以获得帧级特征表示。结合嵌入的帧索引信息，使用两个时间卷积神经网络层来学习特征表示以进行分类。此外，我们开发了一个高性能和高效率的强大基线。由于语义信息的有效探索、分层建模和强大的基线，我们提出的 SGN 以更少的参数实现了最先进的性能。To address the above mentioned limitations of current approaches, we propose a semantics-guided neural network (SGN) which explicitly exploits the semantics and dynamics for high efficient skeleton-based action recognition. Fig. 2 shows the overall framework. We build a hierarchical network by sequentially exploring the joint-level and frame-level dependencies of the skeleton sequence. For better joint-level correlation modeling, besides the dynamics, we incorporate the semantics of joint type (e.g., ‘head’, and ‘hip’) to the GCN layers which enables the content adaptive graph construction and effective message passing among joints within each frame. For better frame-level correlation modeling, we incorporate the semantics of temporal frame index to the network. Particularly, we perform a Spatial MaxPooling (SMP) operation over all the features of the joints within the same frame to obtain framelevel feature representation. Combined with the embedded frame index information, two temporal convolutional neural network layers are used to learn feature representations for classification. In addition, we develop a strong baseline which is of high performance and efficiency. Thanks to the efficient exploration of semantic information, the hierarchical modeling, and the strong baseline, our proposed SGN achieves the state-of-the-art performance with a much smaller number of parameters.

本文主要三个贡献如下：We summarize our three main contributions as follows:

• 显式探索联合语义（帧索引和联合类型），以实现有效的基于骨架的动作识别。以前的工作忽略了语义的重要性，并依赖于高度复杂的深度网络进行动作识别。We propose to explicitly explore the joint semantics (frame index and joint type) for efficient skeleton-based action recognition. Previous works overlook the importance of semantics and rely on deep networks with high complexity for action recognition.
• 提出了一个语义引导的神经网络（SGN）来分层利用联合级别和帧级别的空间和时间相关性。We present a semantics-guided neural network (SGN) to exploit the spatial and temporal correlations at joint-level and frame-level hierarchically.
• 开发了一个轻量级的强基线方法，它比大多数以前的方法更强大。我们希望强基线方法对基于骨架的动作识别的研究有所帮助。We develop a lightweight strong baseline, which is more powerful than most previous methods. We hope the strong baseline will be helpful for the study of skeletonbased action recognition.

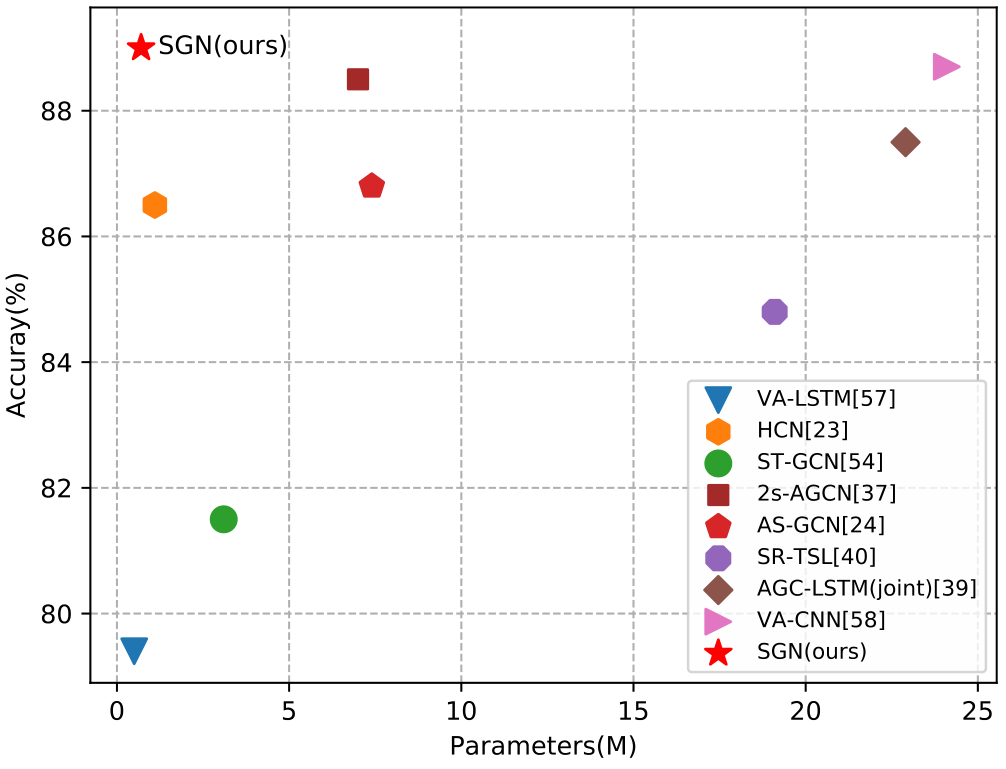
有了上述技术贡献，我们得到了一个高性能、计算效率高的基于骨架的动作识别模型。广泛的消融研究证明了所提出的模型设计的有效性。在基于骨架的动作识别的三个最大的基准数据集上，所提出的模型始终比许多竞争算法实现了卓越的性能，同时模型大小比许多算法小一个数量级（见图 1）。With the above technical contributions, we have obtained a high performance skeleton-based action recognition model with high computational efficiency. Extensive ablation studies demonstrate the effectiveness of the proposed model design. On the three largest benchmark datasets for skeleton-based action recognition, the proposed model consistently achieves superior performances over many competing algorithms while having an order of magnitude smaller model size than many algorithms (see Fig. 1).

2. Related Work

基于骨架的动作识别最近引起了越来越多的关注。最近使用神经网络的作品明显优于使用手工制作特征的传统方法。Skeleton-based action recognition has attracted increasing attentions recently. Recent works using neural networks have significantly outperformed traditional approaches that use hand-crafted features.

Recurrent Neural Network based RNN，例如 LSTM 和 GRU，通常用于对骨架序列的时间动态进行建模。帧中所有关节的 3D 坐标以某种顺序连接起来作为时隙的输入向量。他们没有明确告诉网络哪些维度属于哪个关节。其他一些基于 RNN 的工作倾向于在 RNN 中设计特殊的结构，以使其了解空间结构信息。Shahroudy等人将 LSTM 的单元分为五个子单元，分别对应于五个身体部位，即躯干、两条手臂和两条腿。Liu等人提出了一个时空 LSTM 模型，以利用时域和空间域中关节的上下文依赖性，它们在每个步骤中为不同类型的关节提供数据。在某种程度上，它们区分了不同的关节。Recurrent neural networks, such as LSTM and GRU, are often used to model the temporal dynamics of skeleton sequence. The 3D coordinates of all joints in a frame are concatenated in some order to be the input vector of a time slot. They do not explicitly tell the networks which dimensions belong to which joint. Some other RNN-based works tend to design special structures in RNN to make it aware of the spatial structural information. Shahroudy et al. divide the cell of LSTM into five sub cells corresponding to five body parts, i.e., torso, two arms, and two legs, respectively. Liu et al. propose a spatial-temporal LSTM model to exploit the contextual dependency of joints in both the temporal and spatial domain, where they feed different types of joints at each step. To some extent, they distinguish the different joints.

Convolutional Neural Network based 近年来，在语音、语言序列建模领域，卷积神经网络在准确率和并行度上都表现出优越性。基于骨架的动作识别也是如此。这些基于 CNN 的工作将骨架序列转换为具有一定目标大小的骨架图，然后使用流行的网络（例如 ResNet）来探索空间和时间动态。一些作品通过将关节坐标 (x,y,z) 视为像素的 R、G 和 B 通道，将骨架序列转换为图像。Ke等人将骨架序列转换为四个二维数组，由四个选定的参考关节（即左/右肩、左/右髋）与其他关节之间的相对位置表示。骨架是结构良好的数据，具有明确的高级语义，即帧索引和关节类型。然而，CNN 的内核/过滤器是平移不变的，因此不能直接从这些输入骨架图中感知语义。CNN 期望通过深度网络的大感受野了解此类语义，但效率不高。In recent years, in the field of speech, language sequence modeling, convolutional neural networks demonstrate their superiority in both accuracy and parallelism. The same is true for skeleton-based action recognition. These CNN-based works transform the skeleton sequence to skeleton map of some target size and then use a popular network, such as ResNet, to explore the spatial and temporal dynamics. Some works transform a skeleton sequence to an image by treating the joint coordinate (x,y,z) as the R, G, and B channels of a pixel. Ke et al. transform the skeleton sequence to four 2D arrays, which are represented by the relative position between four selected reference joints (i.e., the left/right shoulder, the left/right hip) and other joints. Skeleton is well structured data with explicit high level semantics, i.e., frame index and joint type. However, the kernels/filters of CNNs are translation invariant and thus cannot directly perceive the semantics from such input skeleton maps. The CNNs are expected to be aware of such semantics through large receptive fields of deep networks, which is not very efficient.

Graph Convolutional Network based 图卷积网络已被证明可有效处理结构化数据，也已用于对结构化骨架数据进行建模。Yan等人提出了一种时空图卷积网络。他们将每个关节视为图的一个节点。表示联合关系的边的存在是由人类基于先验知识预先定义的。为了增强预定义图，Tang 等人定义物理断开和连接的关节对的边，以便更好地构建图形。提出了一种 SR-TSL 模型，以使用数据驱动方法而不是利用人类定义来学习每帧内五个人体部位的图形边缘。双流 GCN 模型基于非本地块学习内容自适应图，并使用它在 GCN 层中传递消息。然而，信息语义并未用于学习 GCN 的图边和消息传递，这使得网络效率较低。Graph convolutional networks, which have been proven to be effective for processing structured data, have also been used to model the structured skeleton data. Yan et al. propose a spatial and temporal graph convolutional network. They treat each joint as a node of the graph. The presence of edge denoting the joint relationship is pre-defined by human based on prior knowledge. To enhance the predefined graph, Tang et al. define the edges for both physically disconnected and connected joint pairs for better constructing the graph. A SR-TSL model is proposed to learn the graph edge of five human body parts within each frame using a datadriven method instead of leveraging human definition. A two-stream GCN model learns a content adaptive graph based on the non-local block and uses it to pass messages in GCN layers. However, the informative semantics is not utilized for learning the graph edge and message passing of GCN, which makes the network less efficient.

Explicit Exploration of Semantics Information 语义的显式探索已在其他领域得到利用，例如机器翻译和图像识别。Ashish等人显式编码序列中标记的位置，以利用机器翻译任务中的序列顺序。Zheng等人将组索引编码为卷积通道表示以保留组顺序信息。然而，对于基于骨架的动作识别，即使这些信息非常重要，也忽略了关节类型和帧索引语义。在我们的工作中，我们建议对关节类型和帧索引进行显式编码，以保留空间和时间身体结构的重要信息。作为探索这种语义的初步尝试，我们希望它能激发这个领域更多的调查和探索。The explicit exploration of semantics has been exploited in other fields, e.g., machine translation and image recognition. Ashish et al. explicitly encode the position of the tokens in the sequence to make use of the order of the sequence in machine translation tasks. Zheng et al. encode the group index into convolutional channel representation to preserve the information of group order. For skeleton-based action recognition, however, the joint type and frame index semantics are overlooked even though such information is very important. In our work, we propose to explicitly encode the joint type and frame index to preserve the important information of the spatial and temporal body structure. As an initial attempt to explore such semantics, we hope it will inspire more investigation and exploration in the community.

3. Semantics-Guided Neural Networks

对于骨架序列，我们通过其语义（关节类型和帧索引）识别关节，并将其与动力学（位置/3D 坐标和速度）一起表示。没有语义，骨架数据将失去重要的时空结构。然而，以前基于 CNN 的工作通常通过将语义隐藏在 2D 骨架图中（例如，对应于不同类型关节的行和对应于帧索引的列）来忽略语义。For a skeleton sequence, we identify a joint by its semantics (joint type and frame index) and represent it together with its dynamics (position/3D coordinates and velocity). Without semantics, the skeleton data will lose the important spatial and temporal structure. Previous CNN-based works, however, typically overlook the semantics by implicitly hiding them in the 2D skeleton map (e.g. with rows corresponding to the different types of joints and columns corresponding to the frame indexes).

我们提出了一种用于基于骨架的动作识别的语义引导神经网络（SGN），并在图 2 中展示了整体的端到端框架。它由一个关节级模块和一个帧级模块组成。我们在以下小节中描述了框架的细节。We propose a semantics-guided neural network (SGN) for skeleton-based action recognition and show the overall end-to-end framework in Fig. 2. It consists of a joint-level module and a frame-level module. We describe the details of the framework in the following subsections.

具体来说，对于骨架序列，我们将所有关节表示为一个集合$\mathcal{S}=\left\{X_t^k\mid t=1,2,\dots ,T;k=1,2,\dots ,J\right\}$，其中 $X_t^k$ 表示在时间 $t$ 的类型 $k$ 的关节。 $T$表示骨架序列的帧数，$J$表示一帧中人体关节的总数。对于在时间 $t$ 的给定类型 $k$ 的关节 $X_t^k$ ，它可以通过其动力学和语义来识别。动力学与关节的 3D 位置有关。语义意味着帧索引 $t$ 和关节类型 $k$。Specifically, for a skeleton sequence, we denote all the joints as a set $\mathcal{S}=\left\{X_t^k\mid t=1,2,\dots ,T;k=1,2,\dots ,J\right\}$, where $X_t^k$ denotes the joint of type $k$ at time $t$. $T$ denotes the number of frames of the skeleton sequence and $J$ denotes the total number of joints of a human body in a frame. For a given joint $X_t^k$ of type $k$ at time $t$, it can be identified by its dynamics and semantics. Dynamics are related to the 3D position of a joint. Semantics means the frame index $t$ and joint type $k$.

3.1. Dynamics Representation

Dynamics Representation 模块包含两个全连接层，使用ReLU作为激活函数，获得位置的编码$\widetilde{{\mathbf{p}}_{t,k}}\in {\mathbb{R}}^{C_1}$。同样的，可以获得速度的编码$\widetilde{{\mathbf{v}}_{t,k}}\in {\mathbb{R}}^{C_1}$。融合位置编码和速度编码可得${\mathbf{z}}_{t,k}=\widetilde{{\mathbf{p}}_{t,k}}+\widetilde{{\mathbf{v}}_{t,k}}\in {\mathbb{R}}^{C_1}$，为了方便，称其为位置速度融合编码。

For a given joint $X_t^k$, we define its dynamics by the position ${\mathbf{p}}_{t,k}={\left(x_{t,k},y_{t,k},z_{t,k}\right)}^T\in {\mathbb{R}}^3$ in the 3D coordinate system, and the velocity ${\mathbf{v}}_{t,k}={\mathbf{p}}_{t,k}-{\mathbf{p}}_{t-1,k}$. We encode/embed the position and velocity into the same high dimensional space, i.e., $\widetilde{{\mathbf{p}}_{t,k}}$ and $\widetilde{{\mathbf{v}}_{t,k}}$, respectively, and fuse them together by summation as
$${\mathbf{z}}_{t,k}=\widetilde{{\mathbf{p}}_{t,k}}+\widetilde{{\mathbf{v}}_{t,k}}\in {\mathbb{R}}^{C_1},$$
where $C_1$ is the dimension of the joint representation. Take the embedding of position as an example, we encode the position ${\mathbf{p}}_{t,k}$ using two fully connected (FC) layers as
$$\widetilde{{\mathbf{p}}_{t,k}}=\sigma \left(W_2\left(\sigma \left(W_1{\mathbf{p}}_{t,k}+{\mathbf{b}}_1\right)\right)+{\mathbf{b}}_2\right),$$
where $W_1\in {\mathbb{R}}^{C_1\times 3}$ and $W_2\in {\mathbb{R}}^{C_1\times C_1}$ are weight matrices, ${\mathbf{b}}_1$ and ${\mathbf{b}}_2$ are the bias vectors, $\sigma$ denotes the ReLU activation function. Similarly, we obtain the embedding for velocity as $\widetilde{{\mathbf{v}}_{t,k}}$.

3.2. Joint-level Module

我们设计了一个关节级模块来利用同一帧中关节的相关性。我们采用图卷积网络（GCN）来探索结构骨架数据的相关性。以前一些基于 GCN 的方法将关节作为节点，它们根据先验知识预先定义图连接（边）或学习内容自适应图。我们同样也学习了内容自适应图，但不同的是，我们将联合类型的语义合并到 GCN 层中，以实现更有效的学习。We design a joint-level module to exploit the correlations of joints in the same frame. We adopt graph convolutional networks (GCN) to explore the correlations for the structural skeleton data. Some previous GCN-based approaches take the joints as nodes and they pre-define the graph connections (edges) based on prior knowledge or learn a content adaptive graph. We also learn a content adaptive graph, but differently we incorporate the semantics of joint type to the GCN layers for more effective learning.

我们通过从两个方面充分利用语义来增强 GCN 层的功能。首先，我们使用关节类型的语义和动态特性来学习帧内节点（不同关节）之间的图连接。关节类型信息有助于学习合适的相邻矩阵（即关节之间的连接权重关系）。以脚和手两个源关节和一个目标关节头为例，直观地说，即使在脚和手的动态特性相同的情况下，脚到头的连接权重值也应该不同于手到头的值。其次，作为关节信息的一部分，关节类型的语义参与了 GCN 层中的消息传递过程。We enhance the power of GCN layers by making full use of the semantics from two aspects. First, we use the semantics of joint type and the dynamics to learn the graph connections among the nodes (different joints) within a frame. The joint type information is helpful for learning suitable adjacent matrix (i.e., relations between joints in terms of connecting weights). Take two source joints, foot and hand, and a target joint head as an example, intuitively, the connection weight value from foot to head should be different from the value from hand to head even when the dynamics of foot and hand are the same. Second, as part of the information of a joint, the semantics of joint types takes part in the message passing process in GCN layers.

使用独热编码${\mathbf{j}}_k$表示关节 $k^{th}$ ，并且获取${\mathbf{j}}_k$的编码$\widetilde{{\mathbf{j}}_k}\in {\mathbb{R}}^{C_1}$。We denote the type of the $k^{th}$ joint (also referred to as type $k$ ) by a one-hot vector ${\mathbf{j}}_k\in {\mathbb{R}}^{d_j}$, where the $k^{\text{th }}$ dimension is one and the others are all zeros. Similar to the encoding of position as in Equ.(2), we obtain the embedding of the $k^{\text{th }}$ joint type as $\widetilde{{\mathbf{j}}_k}\in {\mathbb{R}}^{C_1}$.

位置速度融合编码和节点编码是通过concatenate实现的，即${\mathbf{z}}_{t,k}=\left[{\mathbf{z}}_{t,k},\widetilde{{\mathbf{j}}_k}\right]\in {\mathbb{R}}^{2C_1}$。Given $J$ joints of a skeleton frame, we build a graph of $J$ nodes. We denote the joint representation of joint type $k$ at frame $t$ with both the dynamics and the semantics of joint type as ${\mathbf{z}}_{t,k}=\left[{\mathbf{z}}_{t,k},\widetilde{{\mathbf{j}}_k}\right]\in {\mathbb{R}}^{2C_1}$. All the joints of frame $t$ are then represented by $Z_t=\left({\mathbf{z}}_{t,1};\cdots ;{\mathbf{z}}_{t,J}\right)\in {\mathbb{R}}^{J\times 2C_1}$.

节点与节点之间的相似度$S_t\in \mathbb{J}\times \mathbb{J}$是通过网络学习出来的，对$S_t$的每一行做SoftMax可以得到图的邻接矩阵。Similar to $[49,48,37]$, the edge weight from the $i^{th}$ joint to the $j^{th}$ joint in the same frame $t$ is modeled by their similarity/affinity in the embeded space as
$$S_t(i,j)=\theta {\left({\mathbf{z}}_{t,i}\right)}^T\varphi \left({\mathbf{z}}_{t,j}\right)$$
where $\theta$ and $\varphi$ denote two transformation functions, each implemented by an $\mathrm{F}\mathrm{C}$ layer, i.e., $\theta (\mathbf{x})=W_3\mathbf{x}+{\mathbf{b}}_3\in {\mathbb{R}}^{C_2}$ and $\varphi (\mathbf{x})=W_4\mathbf{x}+{\mathbf{b}}_4\in {\mathbb{R}}^{C_2}$.

By computing the affinities of all the joint pairs in the same frame based on (3), we obtain the adjacency matrix $S_t\in \mathbb{J}\times \mathbb{J}$. Normalization using SoftMax as $[45,48]$ is performed on each row of $S_t$ so that the sum of all the edge values connected to a target node is $1$ . We denote the normalized adjacency matrix by $G_t$.

图2连接方式实现了残差图卷积。GCN的原论文实现方式为$y=\theta \left(I+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}\right)x$，使用renormalization trick: $I_N+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}\to {\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}$得到$H^{(l+1)}=\sigma \left({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{H}^{(l)}{W}^{(l)}\right)$。如renormalization trick所示，$\tilde{A}=A+I_N$。

SGN对GCN公式做出了变形，$Z_t^{\prime }=Y_t+Z_t{W}_z=G_t{Z}_t{W}_y+Z_t{W}_z$，若$W_y=W_z=W$，既有$Z_t^{\prime }=(G_t+I)Z_{t}W$，就可以和GCN原公式对应上了。输出$Z_t^{\prime }\in {\mathbb{R}}^{J\times C_3}$，$Z^{\prime }\in {\mathbb{R}}^{T\times J\times C_3}$，此时$Z_t$融合了各节点的位置信息、速度信息、关节信息。

A residual graph convolution layer is used to realize the massage passing among nodes as
$$\begin{array}{rl}{Y}_t& =G_t{Z}_t{W}_y\\ Z_t^{\prime }& =Y_t+Z_t{W}_z\end{array}$$
where $W_y$ and $W_z$ are transformation matrices. The weight matrices are shared for different temporal frames. $Z_t^{\prime }$ is the output. Note that one can stack multiple residual graph convolution layers to enable further message passing among nodes with the same adjacency matrix $G_t$.

3.3. Frame-level Module

我们设计了一个帧级模块来利用跨帧的相关性。为了让网络知道帧的顺序，我们结合了帧索引的语义来增强帧的表示能力。We design a frame-level module to exploit the correlations across frames. To make the network know the order of frames, we incorporate the semantics of frame index to enhance the representation capability of a frame.

帧索引也采用了独热编码${\mathbf{f}}_t\in {\mathbb{R}}^{d_f}$，同样的，获得帧的编码${\tilde{\mathbf{f}}}_t\in {\mathbb{R}}^{C_3}$。与Joint-level Module模块融合节点编码采用concatenate不同，Frame-level Module融合帧编码采用了add操作，即${\mathbf{z}}_{t,k}^{\prime }={\mathbf{z}}_{t,k}^{\prime }+{\tilde{\mathbf{f}}}_t\in {\mathbb{R}}^{C_3}$。We denote the frame index by a one-hot vector ${\mathbf{f}}_t\in {\mathbb{R}}^{d_f}$. Similar to the encoding of position as in Equ.(2), we obtain the embedding of the frame index as ${\tilde{\mathbf{f}}}_t\in {\mathbb{R}}^{C_3}$. We denote the joint representation corresponding to joint type $k$ at frame $t$ with both the semantics of frame index and the learned feature as ${\mathbf{z}}_{t,k}^{\prime }={\mathbf{z}}_{t,k}^{\prime }+{\tilde{\mathbf{f}}}_t\in {\mathbb{R}}^{C_3}$, where ${\mathbf{z}}_{t,k}^{\prime }=Z_t^{\prime }(k,:)$.

使用SMP下采样合并同一帧中的所有关节信息，得到输出$\in {\mathbb{R}}^{T\times 1\times C_3}$。To merge the information of all joints in a frame, we apply one spatial MaxPooling layer to aggregate them across the joints. The dimension of feature of the sequence is thus $T\times 1\times C_3$.

接下来跟随着两个CNN层，第一个CNN层表示为时间卷积，用来建模帧之间的依赖；第二个CNN层是使用$1\times 1$卷积核进行升维来增强对特征的表示能力。Two $\mathrm{C}\mathrm{N}\mathrm{N}$ layers are applied. The first $\mathrm{C}\mathrm{N}\mathrm{N}$ layer is a temporal convolution layer to model the dependencies of frames. The second CNN layer is used to enhance the representation capability of learned features by mapping it to a high dimension space with kernel size of 1.

之后使用TMP层合并所有帧的信息，输出$\in {\mathbb{R}}^{1\times 1\times C_4}$。接下来，通过全连接层，Softmax分类得到网络最终输出。After the two CNN layers, we apply a temporal MaxPooling layer to aggregate the information of all frames and obtain the sequence level feature representation of $C_4$ dimensions. This is then followed by a fully connected layer with Softmax to perform the classification.

4. 源码

以下代码是我在 microsoft GitHub 源码上做出一定修改，在完成所有代码的修改注释之后再 fork 到自己的 GitHub 上。

如原论文第三节 Semantics-Guided Neural Networks 所示，SGN 网络分为Dynamics Representation, Joint-level Module 和 Frame-level Module 三个部分。

由于论文中的 Embedding 在源码中使用 1x1 的卷积核（而不是论文所写的全连接层）实现的，所以源码中表示特征的深度位于第一个维度（而不是论文的最后一个维度），相关维度信息在下面的代码中都有注释。

SGN网络初始化接受6个参数：

• num_classes 表示类别个数，NTU60 有 60 个类别，NTU120 有120个类别。
• seg 表示视频帧数，在NTU60中，seg=20。
• num_joint 表示关节个数，在NTU60中，num_joint=25。
• channel 包含四个参数，分别对应原论文中的$C_1,C_2,C_3,C_4$。

class SGN(nn.Module):
    def __init__(self, num_classes=60, seg=20, num_joint=25, batch_size=64, channel=(64, 256, 256, 512), bias=True):
        super(SGN, self).__init__()
        (self.c1, self.c2, self.c3, self.c4) = channel  # C1=64, C2=256, C3=256, C4=512
        (self.num_classes, self.seg, self.num_joint, self.batch_size) = (num_classes, seg, num_joint, batch_size)

以下代码生成关节joint和帧frame的onehot编码，其实，个人觉得这部分放在网络的forward部分即可，放在init部分在模型的构件中还需要传入模型的batch_size信息，在forward里面需要判断input的batch_size是否相等。

        if not self.training: self.batch_size = 32 * 5
        self.spa = self.one_hot(self.batch_size, self.num_joint, self.seg)  # [bs, seg, num_joint, num_joint]
        self.spa = self.spa.permute(0, 3, 2, 1).cuda()  # [bs, num_joint, num_joint, seg]
        self.tem = self.one_hot(self.batch_size, self.seg, self.num_joint)  # [bs, num_joint, seg, seg]
        self.tem = self.tem.permute(0, 3, 1, 2).cuda()  # [bs, seg, num_joint, seg]

下面两句完成Dynamics Representation部分的模块创建。

        # Joint Embedding (两个全连接层, 3->64->C1)
        self.joint_embed = embed(3, self.c1, norm=True, bias=bias)
        # Velocity Embedding (两个全连接层, 3->64->C1)
        self.dif_embed = embed(3, self.c1, norm=True, bias=bias)

原论文的Embedding使用全连接层完成，而，源码使用1x1的卷积层完成这一操作，具体代码如下。

class embed(nn.Module):
    def __init__(self, dim=3, dim1=128, norm=True, bias=False):
        super(embed, self).__init__()

        if norm:  # 这里 norm=false 时直接用 nn.Identity 代码会简洁一些
            self.cnn = nn.Sequential(norm_data(dim),
                                     cnn1x1(dim, 64, bias=bias),
                                     nn.ReLU(),
                                     cnn1x1(64, dim1, bias=bias),
                                     nn.ReLU(), )
        else:
            self.cnn = nn.Sequential(cnn1x1(dim, 64, bias=bias),
                                     nn.ReLU(),
                                     cnn1x1(64, dim1, bias=bias),
                                     nn.ReLU(), )

    def forward(self, x):
        x = self.cnn(x)
        return x

Joint-level Module 包含的代码通过下面代码实现。

        # Spatial Embedding (两个全连接层, num_joint->64->C1)
        self.spa_embed = embed(num_joint, self.c1, norm=False, bias=bias)
        # 计算邻接矩阵 [bs, seg, num_joint, 2C1=128] -> [bs, seg, num_joint, num_joint]
        self.compute_g1 = compute_g_spa(2 * self.c1, self.c2, bias=bias)
        # [bs, 2C1, num_joint, seg] -> [bs, 2C1, num_joint, seg]
        self.gcn1 = gcn_spa(2 * self.c1, 2 * self.c1, bias=bias)
        # [bs, 2C1, num_joint, seg] -> [bs, C3, num_joint, seg]
        self.gcn2 = gcn_spa(2 * self.c1, self.c3, bias=bias)
        # [bs, C3, num_joint, seg] -> [bs, C3, num_joint, seg]
        self.gcn3 = gcn_spa(self.c3, self.c3, bias=bias)

Frame-level Module 包含的代码通过下面代码实现。

        # Temporal Embedding (两个全连接层, seg->64->C3)
        self.tem_embed = embed(self.seg, self.c3, norm=False, bias=bias)
        # MaxPooling -> Conv - > BN -> ReLU -> Conv - > BN -> ReLU
        self.cnn = local(self.c3, self.c4, bias=bias)
        # Temporal MaxPooling
        self.maxpool = nn.AdaptiveMaxPool2d((1, 1))

然后通过一个全连接层得到网络的输出：

        self.fc = nn.Linear(self.c4, self.num_classes)

网络的前向传播为：

class embed(nn.Module):
    def __init__(self, num_classes=60, seg=20, num_joint=25, batch_size=64, channel=(64, 256, 256, 512), bias=True):
        pass
        
    def forward(self, input):
        bs, step, dim = input.size()  # [bs, seg, num_joints*3]
        num_joints = dim // 3
        assert bs == self.batch_size, f'the batch size of input must equal to {self.batch_size}'
        assert step == self.seg, f'the frame number of input must equal to {self.seg}'
        assert num_joints == self.num_joint, f'the joints number of input must equal to {self.num_joint}'

        # Dynamic Representation
        input = input.view((bs, step, num_joints, 3))  # [bs, seg, num_joints, 3]
        input = input.permute(0, 3, 2, 1).contiguous()  # [bs, 3, num_joints, seg]
        dif = input[:, :, :, 1:] - input[:, :, :, 0:-1]  # [bs, 3, num_joints, seg-1]  Velocity
        # 由于相减缺少一个维度, 将初始时刻的速度设置为0即可
        # [bs, 3, num_joints, seg-1] -> [bs, 3, num_joints, seg]
        dif = torch.cat([dif.new(bs, dif.size(1), num_joints, 1).zero_(), dif], dim=-1)
        # [bs, 3, num_joints, seg] -> [bs, 64, num_joints, seg]
        pos = self.joint_embed(input)
        # [bs, 3, num_joints, seg] -> [bs, 64, num_joints, seg]
        dif = self.dif_embed(dif)
        # -> [bs, 64, num_joints, seg]
        dy = pos + dif

        # Joint-level Module
        # [bs, num_joint, num_joint, seg] -> [bs, 64, num_joint, seg]
        spa1 = self.spa_embed(self.spa)
        # -> [bs, 128, num_joint, seg]
        input = torch.cat([dy, spa1], 1)
        # -> [bs, seg, num_joint, num_joint]
        g = self.compute_g1(input)
        # -> [bs, 128, num_joint, seg]
        input = self.gcn1(input, g)
        # -> [bs, 256, num_joint, seg]
        input = self.gcn2(input, g)
        # -> [bs, 256, num_joint, seg]
        input = self.gcn3(input, g)
        # Frame-level Module
        # [bs, seg, num_joint, seg] -> [bs, 256, num_joint, seg]
        tem1 = self.tem_embed(self.tem)
        # -> [bs, 256, num_joint, seg]
        input = input + tem1
        # -> [bs, C3=512, 1, seg=20]
        input = self.cnn(input)
        # Classification
        # [bs, C3=512, 1, seg=20] -> [bs, C3=512, 1, 1]
        output = self.maxpool(input)
        # -> [bs, C3=512]
        output = torch.flatten(output, 1)
        # -> [bs, C3=60]
        output = self.fc(output)

        return output

model.py 全部代码：

# Copyright (c) Microsoft Corporation. All rights reserved.
# Licensed under the MIT License.
from torch import nn
import torch
import math


class SGN(nn.Module):
    def __init__(self, num_classes=60, seg=20, num_joint=25, batch_size=64, channel=(64, 256, 256, 512), bias=True):
        super(SGN, self).__init__()

        (self.c1, self.c2, self.c3, self.c4) = channel  # C1=64, C2=256, C3=256, C4=512
        (self.num_classes, self.seg, self.num_joint, self.batch_size) = (num_classes, seg, num_joint, batch_size)

        if not self.training: self.batch_size = 32 * 5
        self.spa = self.one_hot(self.batch_size, self.num_joint, self.seg)  # [bs, seg, num_joint, num_joint]
        self.spa = self.spa.permute(0, 3, 2, 1).cuda()  # [bs, num_joint, num_joint, seg]
        self.tem = self.one_hot(self.batch_size, self.seg, self.num_joint)  # [bs, num_joint, seg, seg]
        self.tem = self.tem.permute(0, 3, 1, 2).cuda()  # [bs, seg, num_joint, seg]

        # Joint Embedding (两个全连接层, 3->64->C1)
        self.joint_embed = embed(3, self.c1, norm=True, bias=bias)
        # Velocity Embedding (两个全连接层, 3->64->C1)
        self.dif_embed = embed(3, self.c1, norm=True, bias=bias)

        # Spatial Embedding (两个全连接层, num_joint->64->C1)
        self.spa_embed = embed(num_joint, self.c1, norm=False, bias=bias)
        # 计算邻接矩阵 [bs, seg, num_joint, 2C1=128] -> [bs, seg, num_joint, num_joint]
        self.compute_g1 = compute_g_spa(2 * self.c1, self.c2, bias=bias)
        # [bs, 2C1, num_joint, seg] -> [bs, 2C1, num_joint, seg]
        self.gcn1 = gcn_spa(2 * self.c1, 2 * self.c1, bias=bias)
        # [bs, 2C1, num_joint, seg] -> [bs, C3, num_joint, seg]
        self.gcn2 = gcn_spa(2 * self.c1, self.c3, bias=bias)
        # [bs, C3, num_joint, seg] -> [bs, C3, num_joint, seg]
        self.gcn3 = gcn_spa(self.c3, self.c3, bias=bias)

        # Temporal Embedding (两个全连接层, seg->64->C3)
        self.tem_embed = embed(self.seg, self.c3, norm=False, bias=bias)
        # MaxPooling -> Conv - > BN -> ReLU -> Conv - > BN -> ReLU
        self.cnn = local(self.c3, self.c4, bias=bias)
        # Temporal MaxPooling
        self.maxpool = nn.AdaptiveMaxPool2d((1, 1))


        self.fc = nn.Linear(self.c4, self.num_classes)

        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                n = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
                m.weight.data.normal_(0, math.sqrt(2. / n))

        nn.init.constant_(self.gcn1.w.cnn.weight, 0)
        nn.init.constant_(self.gcn2.w.cnn.weight, 0)
        nn.init.constant_(self.gcn3.w.cnn.weight, 0)

    def forward(self, input):
        bs, step, dim = input.size()  # [bs, seg, num_joints*3]
        num_joints = dim // 3
        assert bs == self.batch_size, f'the batch size of input must equal to {self.batch_size}'
        assert step == self.seg, f'the frame number of input must equal to {self.seg}'
        assert num_joints == self.num_joint, f'the joints number of input must equal to {self.num_joint}'

        # Dynamic Representation
        input = input.view((bs, step, num_joints, 3))  # [bs, seg, num_joints, 3]
        input = input.permute(0, 3, 2, 1).contiguous()  # [bs, 3, num_joints, seg]
        dif = input[:, :, :, 1:] - input[:, :, :, 0:-1]  # [bs, 3, num_joints, seg-1]  Velocity
        # 由于相减缺少一个维度, 将初始时刻的速度设置为0即可
        # [bs, 3, num_joints, seg-1] -> [bs, 3, num_joints, seg]
        dif = torch.cat([dif.new(bs, dif.size(1), num_joints, 1).zero_(), dif], dim=-1)
        # [bs, 3, num_joints, seg] -> [bs, 64, num_joints, seg]
        pos = self.joint_embed(input)
        # [bs, 3, num_joints, seg] -> [bs, 64, num_joints, seg]
        dif = self.dif_embed(dif)
        # -> [bs, 64, num_joints, seg]
        dy = pos + dif

        # Joint-level Module
        # [bs, num_joint, num_joint, seg] -> [bs, 64, num_joint, seg]
        spa1 = self.spa_embed(self.spa)
        # -> [bs, 128, num_joint, seg]
        input = torch.cat([dy, spa1], 1)
        # -> [bs, seg, num_joint, num_joint]
        g = self.compute_g1(input)
        # -> [bs, 128, num_joint, seg]
        input = self.gcn1(input, g)
        # -> [bs, 256, num_joint, seg]
        input = self.gcn2(input, g)
        # -> [bs, 256, num_joint, seg]
        input = self.gcn3(input, g)
        # Frame-level Module
        # [bs, seg, num_joint, seg] -> [bs, 256, num_joint, seg]
        tem1 = self.tem_embed(self.tem)
        # -> [bs, 256, num_joint, seg]
        input = input + tem1
        # -> [bs, C3=512, 1, seg=20]
        input = self.cnn(input)
        # Classification
        # [bs, C3=512, 1, seg=20] -> [bs, C3=512, 1, 1]
        output = self.maxpool(input)
        # -> [bs, C3=512]
        output = torch.flatten(output, 1)
        # -> [bs, C3=60]
        output = self.fc(output)

        return output

    def one_hot(self, bs, spa, tem):
        # 生成 onehot 编码
        y = torch.arange(spa).unsqueeze(-1)
        y_onehot = torch.FloatTensor(spa, spa).zero_()

        y_onehot.scatter_(1, y, 1)

        y_onehot = y_onehot.unsqueeze(0).unsqueeze(0)
        y_onehot = y_onehot.repeat(bs, tem, 1, 1)

        return y_onehot


class norm_data(nn.Module):
    def __init__(self, dim=64, num_joint=25):
        super(norm_data, self).__init__()

        self.bn = nn.BatchNorm1d(dim * num_joint)

    def forward(self, x):
        bs, c, num_joints, step = x.size()
        x = x.view(bs, -1, step)
        x = self.bn(x)
        x = x.view(bs, -1, num_joints, step).contiguous()
        return x


class embed(nn.Module):
    def __init__(self, dim=3, dim1=128, norm=True, bias=False):
        super(embed, self).__init__()

        if norm:  # 这里 norm=false 时直接用 nn.Identity 代码会简洁一些
            self.cnn = nn.Sequential(norm_data(dim),
                                     cnn1x1(dim, 64, bias=bias),
                                     nn.ReLU(),
                                     cnn1x1(64, dim1, bias=bias),
                                     nn.ReLU(), )
        else:
            self.cnn = nn.Sequential(cnn1x1(dim, 64, bias=bias),
                                     nn.ReLU(),
                                     cnn1x1(64, dim1, bias=bias),
                                     nn.ReLU(), )

    def forward(self, x):
        x = self.cnn(x)
        return x


class cnn1x1(nn.Module):
    def __init__(self, dim1=3, dim2=3, bias=True):
        super(cnn1x1, self).__init__()
        self.cnn = nn.Conv2d(dim1, dim2, kernel_size=1, bias=bias)

    def forward(self, x):
        x = self.cnn(x)
        return x


class local(nn.Module):
    def __init__(self, dim1=3, dim2=3, bias=False):  # dim1 = 256, dim2 = 512
        super(local, self).__init__()
        self.maxpool = nn.AdaptiveMaxPool2d((1, 20))
        self.cnn1 = nn.Conv2d(dim1, dim1, kernel_size=(1, 3), padding=(0, 1), bias=bias)
        self.bn1 = nn.BatchNorm2d(dim1)
        self.relu = nn.ReLU()
        self.cnn2 = nn.Conv2d(dim1, dim2, kernel_size=1, bias=bias)
        self.bn2 = nn.BatchNorm2d(dim2)
        self.dropout = nn.Dropout2d(0.2)

    def forward(self, x1):
        x1 = self.maxpool(x1)
        x = self.cnn1(x1)
        x = self.bn1(x)
        x = self.relu(x)
        x = self.dropout(x)
        x = self.cnn2(x)
        x = self.bn2(x)
        x = self.relu(x)

        return x


class gcn_spa(nn.Module):
    def __init__(self, in_feature, out_feature, bias=False):  # in_feature = 128, out_feature = 128
        super(gcn_spa, self).__init__()
        self.w = cnn1x1(in_feature, out_feature, bias=False)
        self.w1 = cnn1x1(in_feature, out_feature, bias=bias)
        self.relu = nn.ReLU()
        self.bn = nn.BatchNorm2d(out_feature)

    def forward(self, x1, g):
        x = x1.permute(0, 3, 2, 1).contiguous()
        x = g.matmul(x)
        x = x.permute(0, 3, 2, 1).contiguous()
        x = self.w(x) + self.w1(x1)
        x = self.relu(self.bn(x))
        return x


class compute_g_spa(nn.Module):  # 计算邻接矩阵
    def __init__(self, dim1=64 * 3, dim2=64 * 3, bias=False):
        super(compute_g_spa, self).__init__()
        self.dim1 = dim1  # 128 = 64 + 64
        self.dim2 = dim2  # 256
        self.g1 = cnn1x1(self.dim1, self.dim2, bias=bias)
        self.g2 = cnn1x1(self.dim1, self.dim2, bias=bias)
        self.softmax = nn.Softmax(dim=-1)

    def forward(self, x1):
        g1 = self.g1(x1).permute(0, 3, 2, 1).contiguous()
        g2 = self.g2(x1).permute(0, 3, 1, 2).contiguous()
        g3 = g1.matmul(g2)
        g = self.softmax(g3)
        return g


if __name__ == '__main__':
    x = torch.rand(4, 20, 75).cuda()
    model = SGN(num_classes=60, seg=20, num_joint=25, batch_size=4).cuda()
    model.train()
    y = model(x)
    pass