七、神经网络(深度学习算法)
7.1 认识神经网络
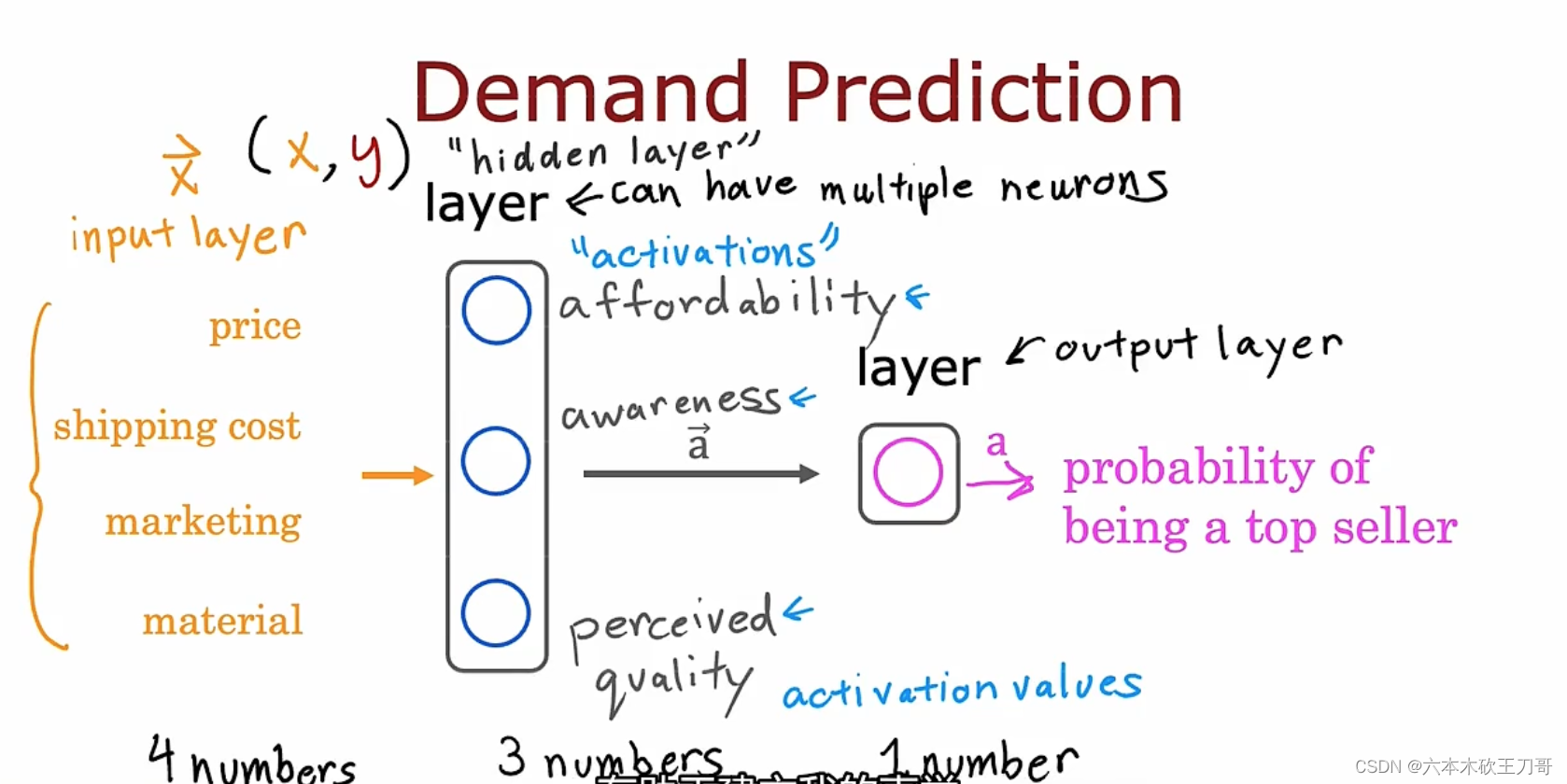
单一隐藏层的神经网络,输入层,隐藏层,输出层,虽然在这个例子中我们可以给隐藏层三个神经元取名字,但是没有必要特别关注隐藏层。如果把输入层遮掉,只留下hidden layer和output layer,就可以理解为一个逻辑回归模型。
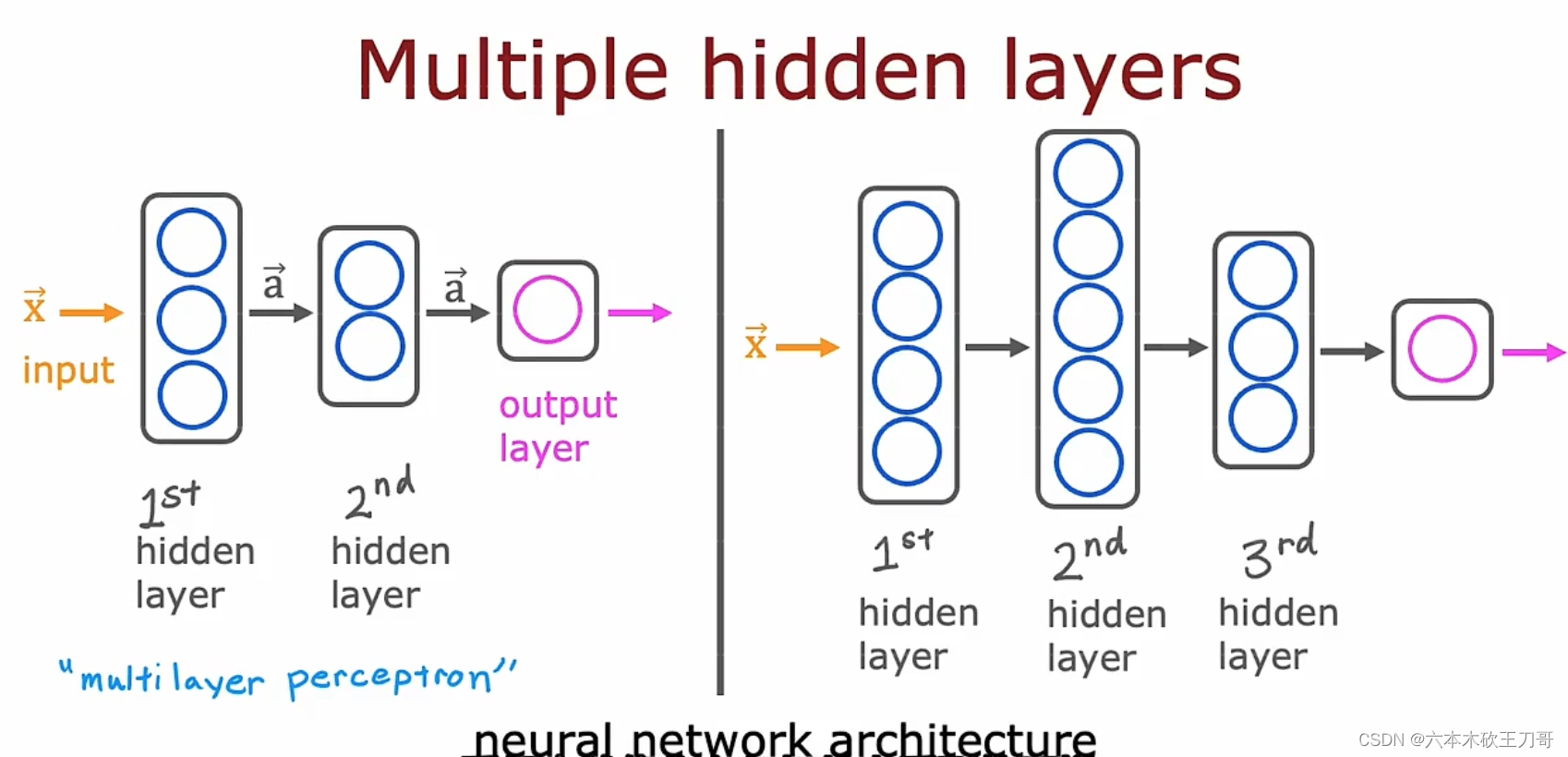
拥有多个隐藏层的神经网络:
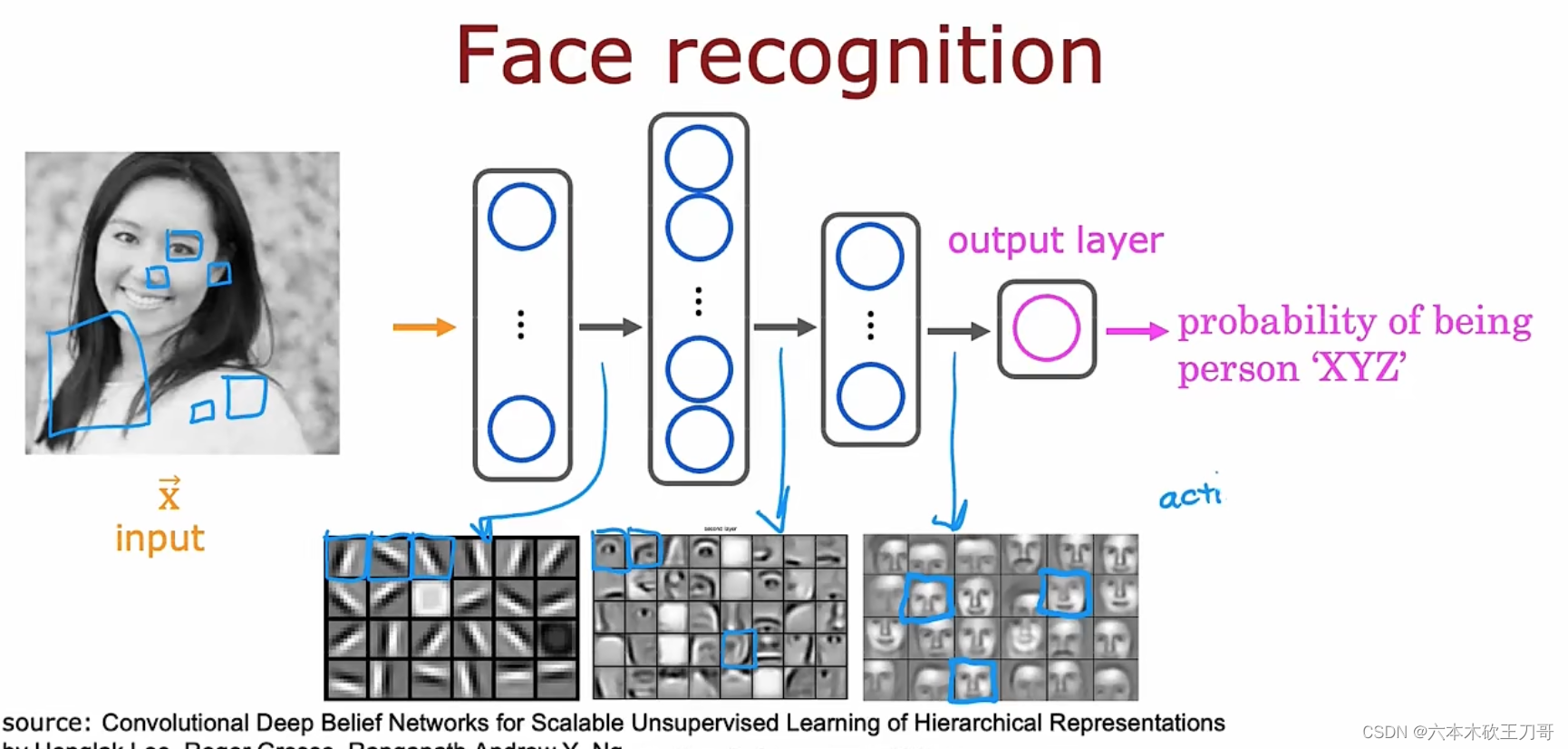
神经网络应用举例:图像感知 Recogonition image,计算机识别人像和汽车是靠像素点的亮度值,图像数据特征向量特征值很多,显然再继续用之前的算法难以处理这么庞大的数据。
7.2 如何在神经网络上推理
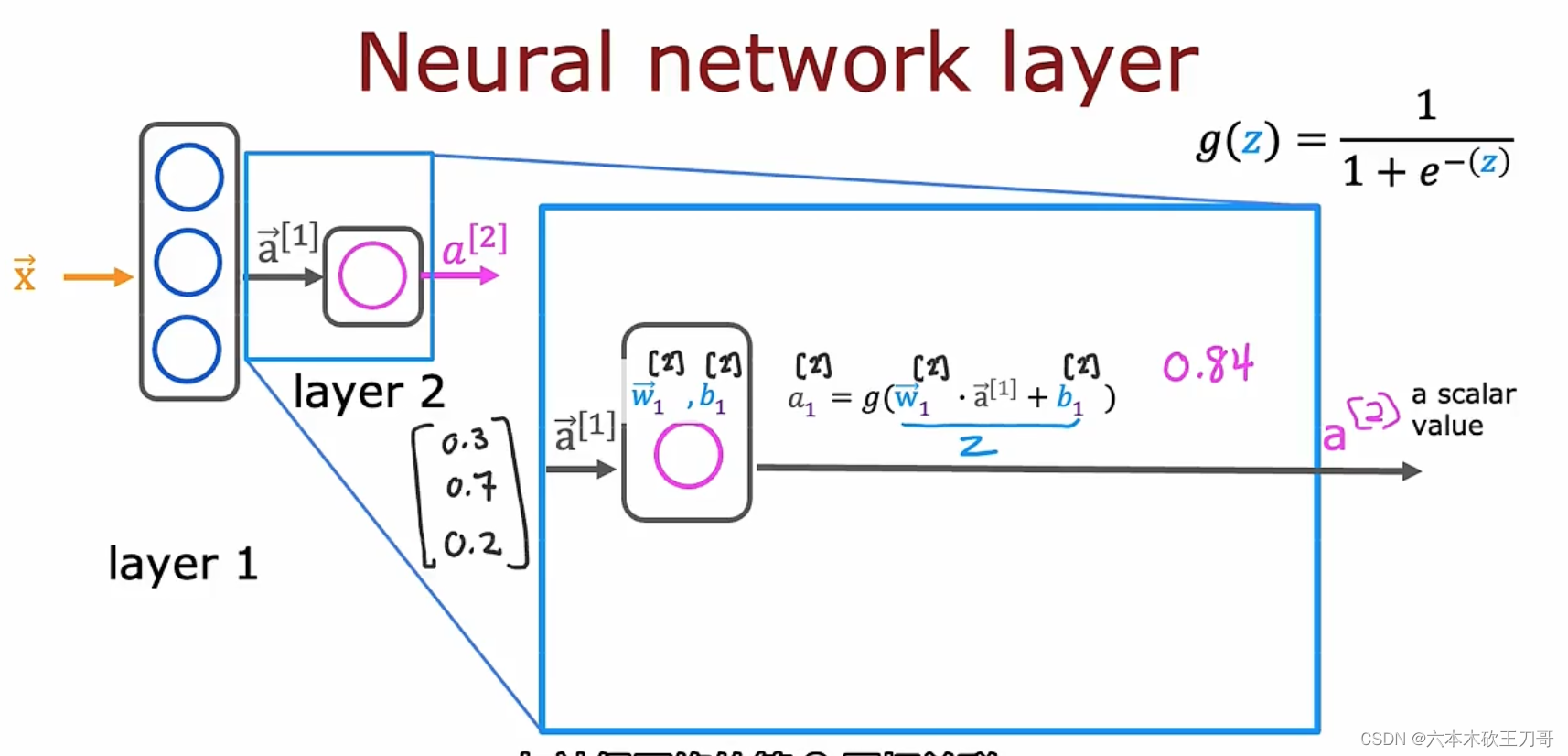
7.2.1 神经网络中的网络层
计算输入向量x如何在各层之间传播,其中a的右上标为第n层的输出,每个神经元的函数是Sigmoid函数。
7.2.2 更复杂的网络
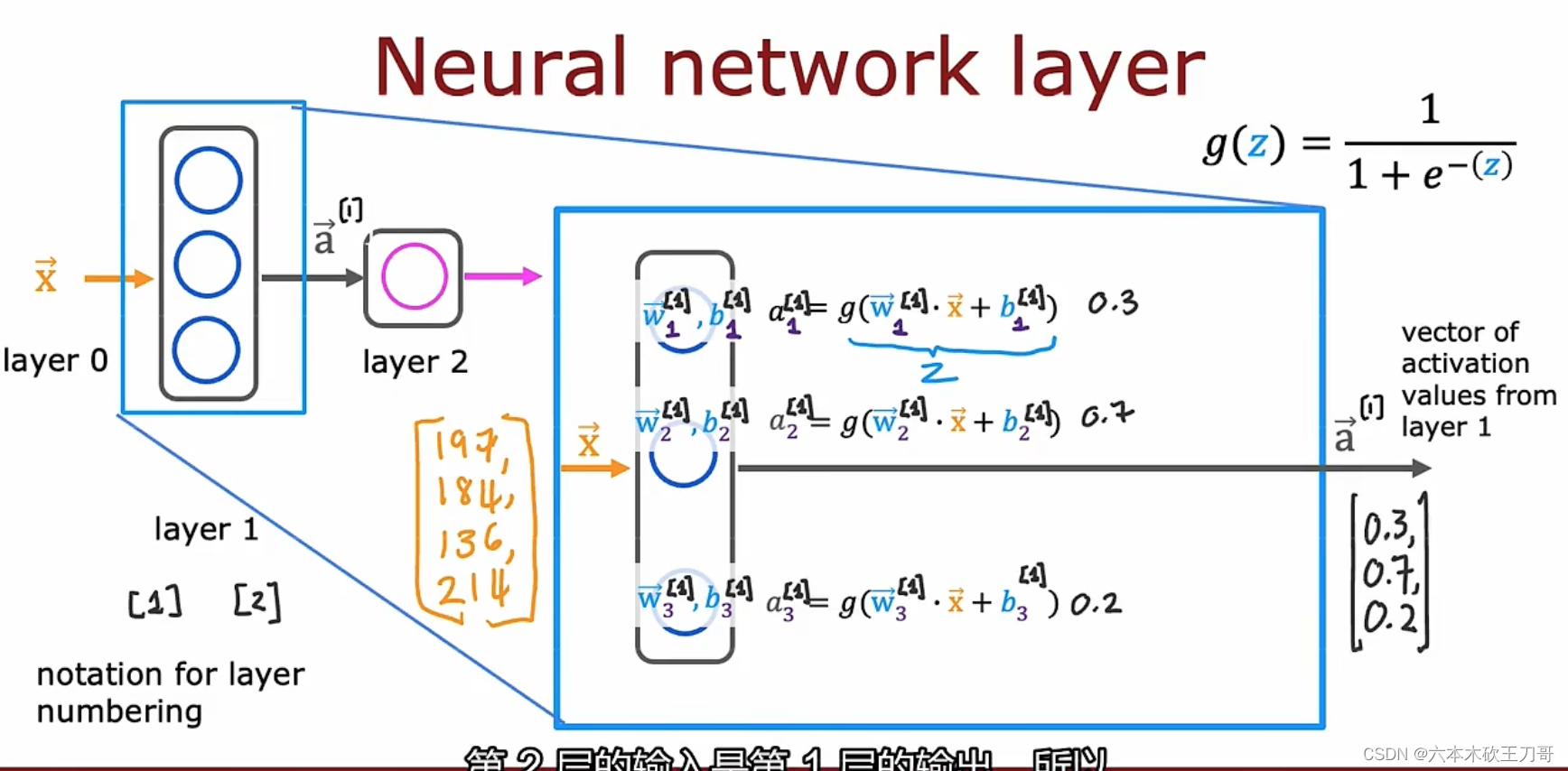
注意每一层隐藏层的上下标,一般不把输入层算进去,也就是输入层是layer 0,这里我们终点讨论第三层,我们把第三层提取出来。经过第三层的激活函数Sigmoid,我们得到新的输出a3向量,我们要注意每个w,b的上标是根据它所在的隐藏层位置所决定的。(注意每个点的w和a都是向量)
以上,最后推导出了传播的公式,输入![\vec{a} {^{[l-1]}}](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUN2ZWMlN0JhJTdEJTIwJTdCJTVFJTdCJTVCbC0xJTVEJTdEJTdE)
![\vec{w} {_{j}^{[l]}}](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUN2ZWMlN0J3JTdEJTIwJTdCXyU3QmolN0QlNUUlN0IlNUJsJTVEJTdEJTdE)
![b {_{j}^{[l]}}](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9iJTIwJTdCXyU3QmolN0QlNUUlN0IlNUJsJTVEJTdEJTdE)
![a {_{j}^{[l]}}](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9hJTIwJTdCXyU3QmolN0QlNUUlN0IlNUJsJTVEJTdEJTdE)
7.2.3 神经网络前向传播
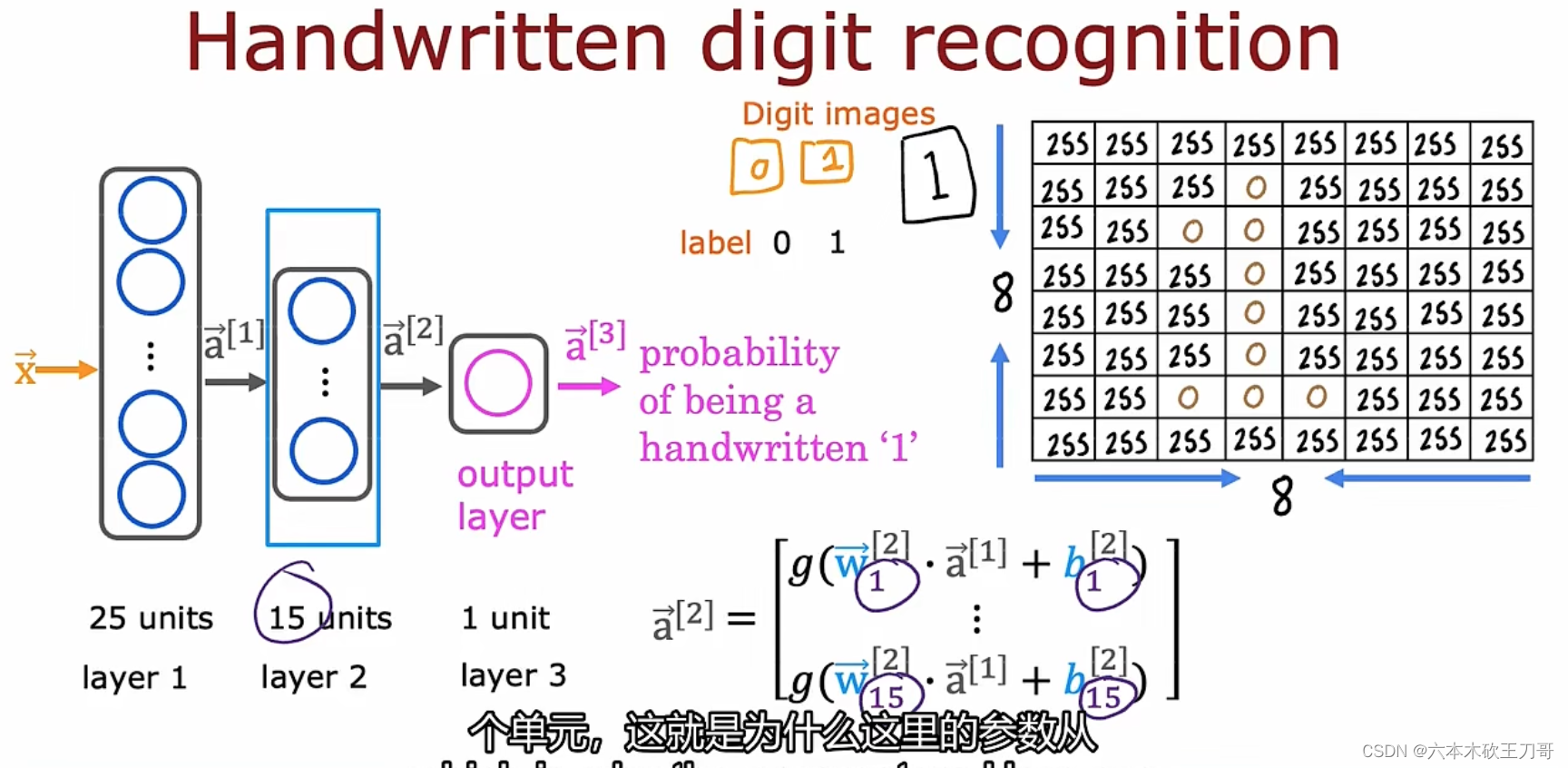
案例:手写识别0和1,输入是下图的中8x8矩阵,这个矩阵是显示数字1的图像。之后需要每层计算, 从左往右计算,要传播神经元的激活值。
在第一层中有25个单元,输入x向量需要在每个单元中计算一次并输出a1向量。
第二层有15个神经元或者15个单元,继续计算输出a2向量。
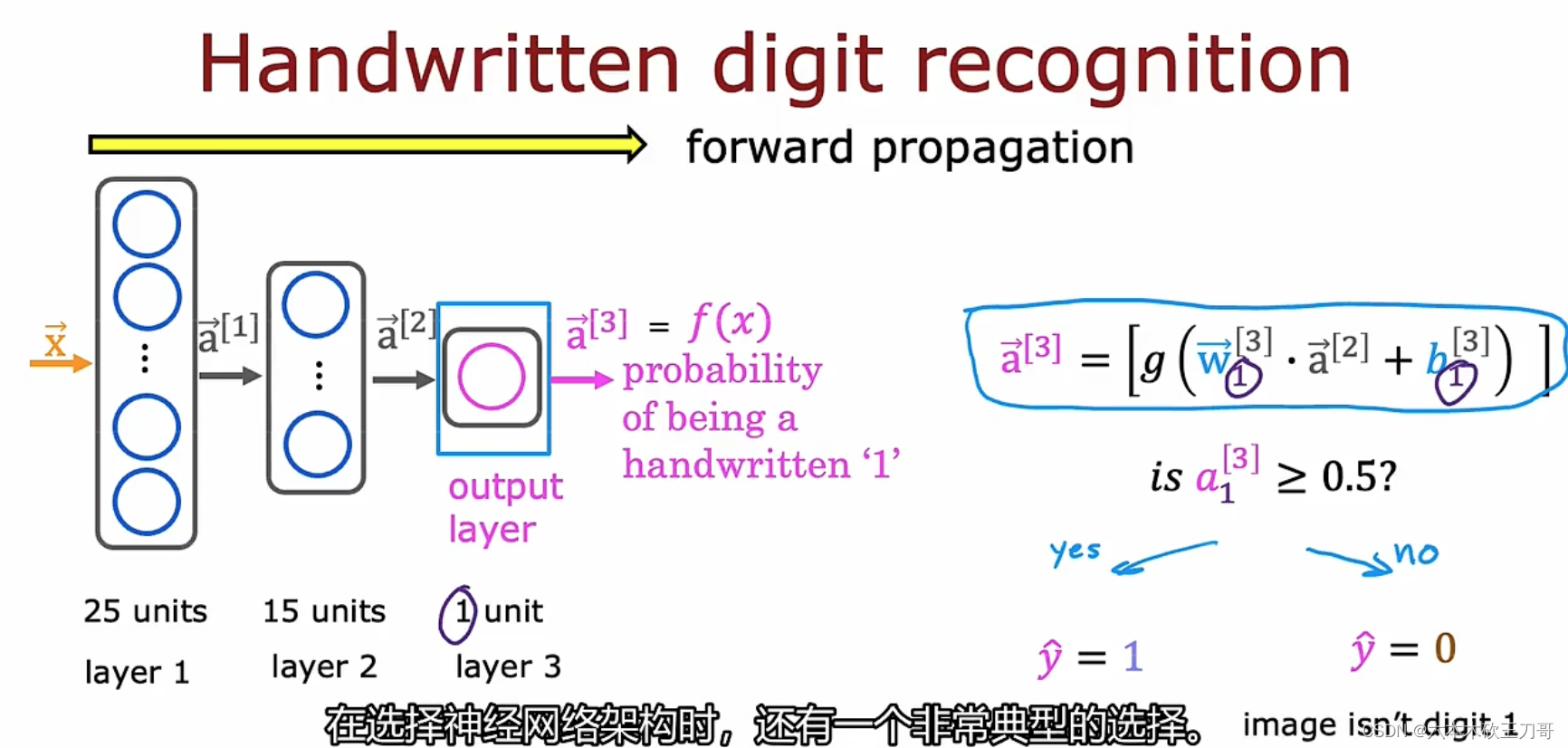
最后一层只有一个单元,输出a3向量,a3向量只有一个值,我们也可以用f(x)来表示输出(线性回归和逻辑回归都是用f(x)来表示,神经网络也同样可以),这样往前计算的方式也叫前向传播,与之对应的是反向传播。
7.3 如何用代码实现推理
7.3.1 代码推理
接下来用tensorFlow来实现一个案例。
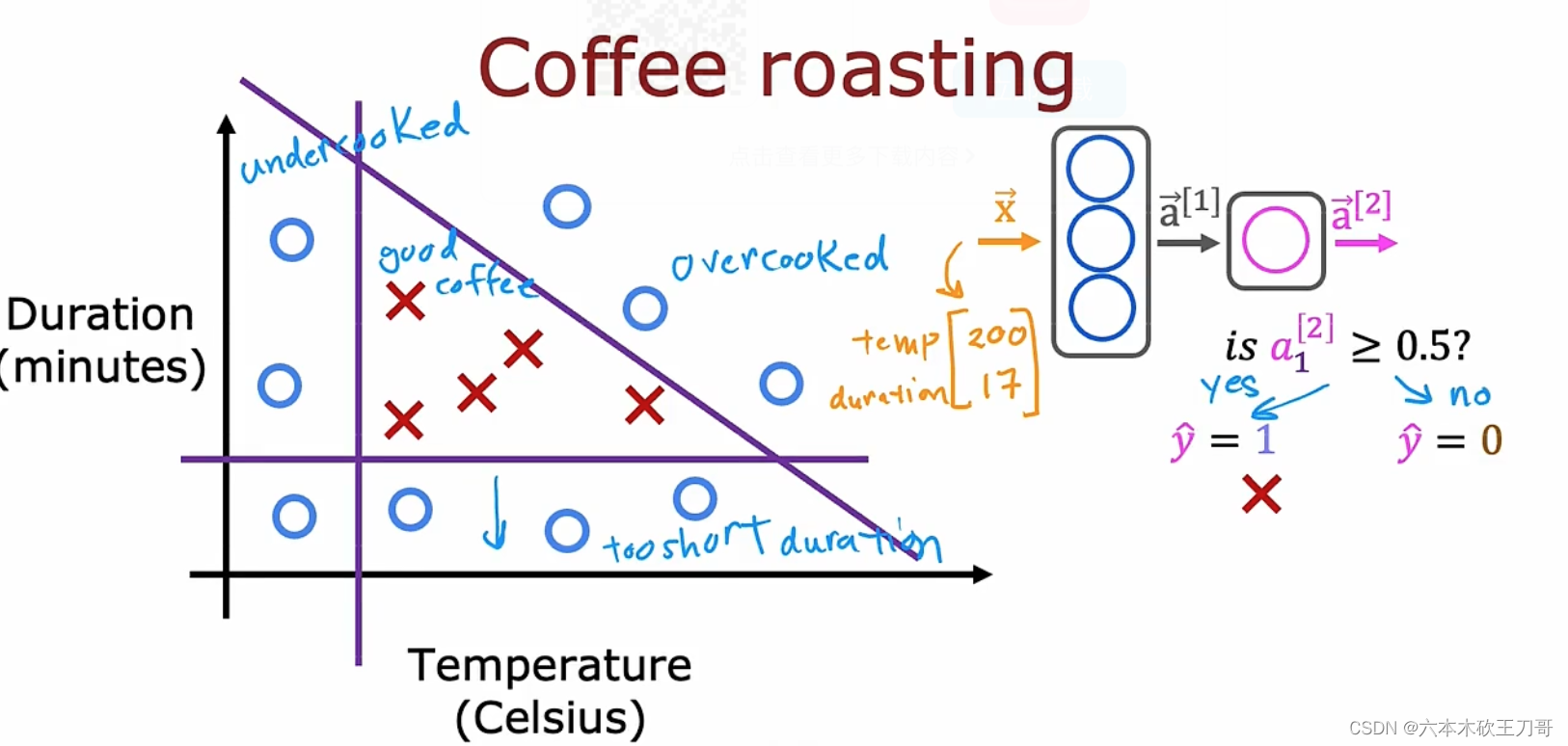
案例:是否能烘培出好的咖啡豆,其中能控制的变量是烘培的温度和持续的时间。下图中的X表示烤的不错的正向案例,O表示烤得不好的案例。
假设温度太低或者持续时间太低,或者两者都很高的情况下,咖啡豆质量变差,根据这个训练集,然后判断某个输入,得到的输出属于yes或者no。 例如温度是200,时间是17分钟,神经网络输入向量是[200, 17],可否根据输出来判断是否是好咖啡。
使用TensorFlow构建咖啡豆神经网络程序,可以定义每一层神经网络的参数,以及输入输出。下列x是输入向量,layer_1是第一个隐藏层,它的名字可以取为Dense,经过这一层后的输出是a1向量。然后设置第二层同理,最后获得输出,判断输出属于哪个类别。
回到01识别的例子中,可以写出类似的TensorFlow程序。
7.3.2 TensorFlow数据形式
NumPy和TensorFlow的数据形式是不一样的。
numPy中用两个方括号来表示多维矩阵。
在TensorFlow中,习惯使用矩阵来表示数据,因为通常数据量很大,使用矩阵而不是一维数据可以更好的处理数据。下图中最后的一个方括号表示是一个一维数组,而上面两个方括号形式是矩阵表示。
当然,以下这两种形式都是numpy的,后面的tensor类型才是TensorFlow内部转换的,有利于内部的计算,当读回数据到Numpy的时候,转换回numpy类型的矩阵
回到刚开始的问题,我们使用1X2的矩阵来表示输入。
如果我们打印输出a1的话,结果会出现一个Tensor张量类型,这是TensorFlow中为了有效存储和执行矩阵计算而创建的类型,并且这个输出结果是一个1X3的向量,它的数据类型是float32。张量表示更加通用,但是这里可以把矩阵和张量视为同一种类型。
NumPy和TensorFlow中的数据表示由于历史原因而有所差别,但是如果想要把Tensor类型转换回NumPy类型,可以使用a1.numpy()这样的转换语句。
对于下一层,也是同理。
在编写代码的时候,需要注意这两种形式的使用和转换。
7.3.3 搭建一个神经网络
之前的实现是每次通过一个网络计算,然后得到结果传输到下一个网络,但是TensorFlow可以把网络通过顺序结合在一起成为一个model,这是Sequential framewrok的作用。
通过把数据组装成矩阵的形式,分别作为输入和输出来训练网络,此时可以调用compile和fit函数(下一节会涉及),这样就不用显式的把数据输入和输出网络了。
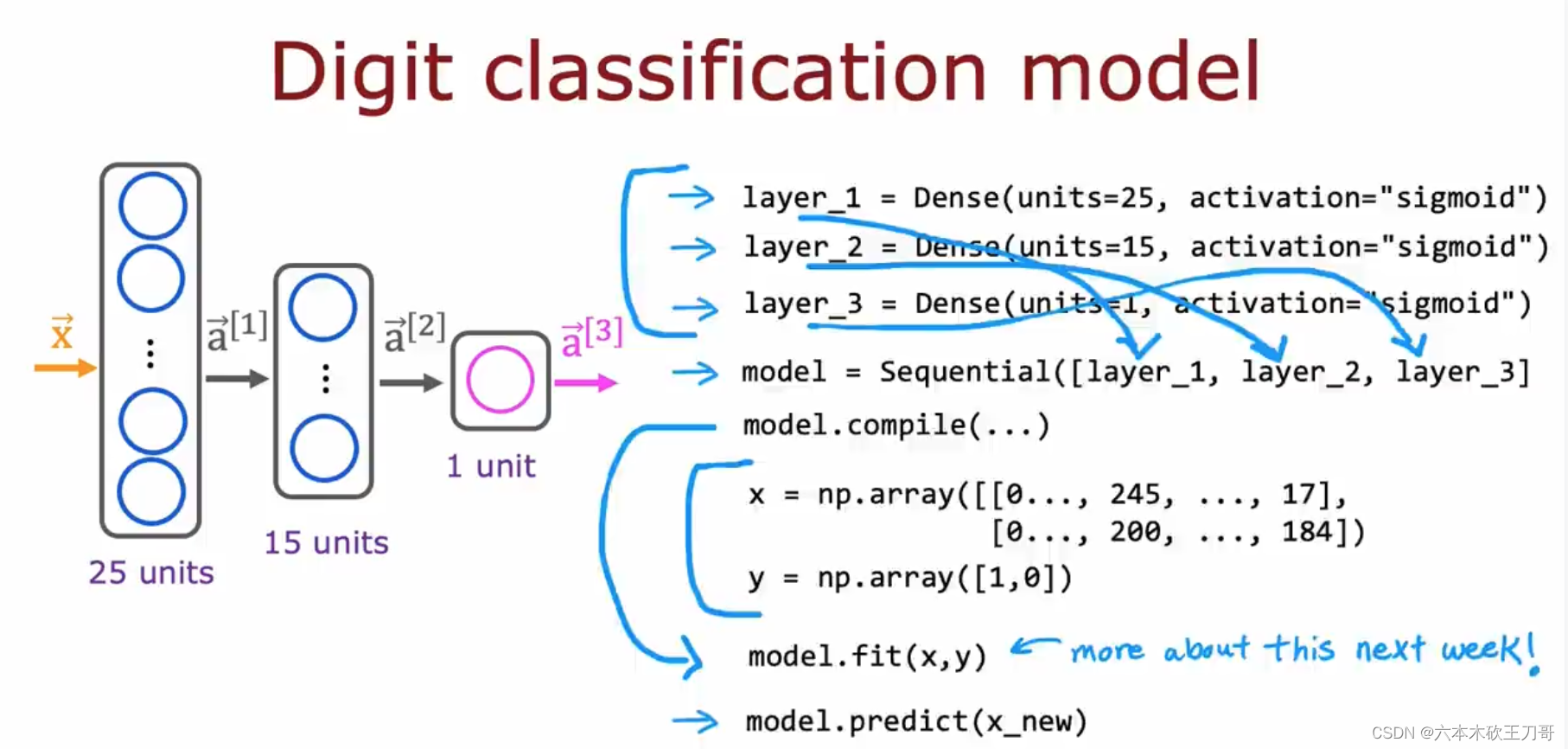
接下来继续以数字识别为例子,我们可以用Sequential函数来建立网络。
接下来还可以用更紧凑的方式来建立model。
虽然库函数的调用帮助我们更好的运行我们的程序,但是依然需要搞清楚其中的原理,下一节展示了如何用python来实现。
7.4 实现前向传播
7.4.1 单个神经网络上的前向传播
继续以烤咖啡都为案例,用python代码来模拟库函数的过程如下,我们把每个单元的计算拆解为一组代码,输入x,输出a2,图中就是计算的过程。
7.4.2 前向传播的一般实现
这节会介绍有些通用的方式而不是之前的硬编码。给出一个Dense函数,输入参数是输入向量,W和b,所以以第一层为例子,我们把每个单元的w和b堆叠成矩阵和数组的形式,其中w矩阵是以三个列向量组成的,b是一个一维数组,输入a向量也是一个一维数组,有了这些输入参数,我们可以实现Dense函数的细节,首先units代表W矩阵第二个维度的数值,在这里是三个列向量,然后aout是初始化输出向量,接下来的for循环是利用W的每个列向量和输入向量加上b,计算输出aout每个维度的数值,一共计算三次,最后返回结果。
得到这个dense函数的实现之后,我们可以定义sequential函数,利用dense函数来实现内部的原理前向传播的原理。
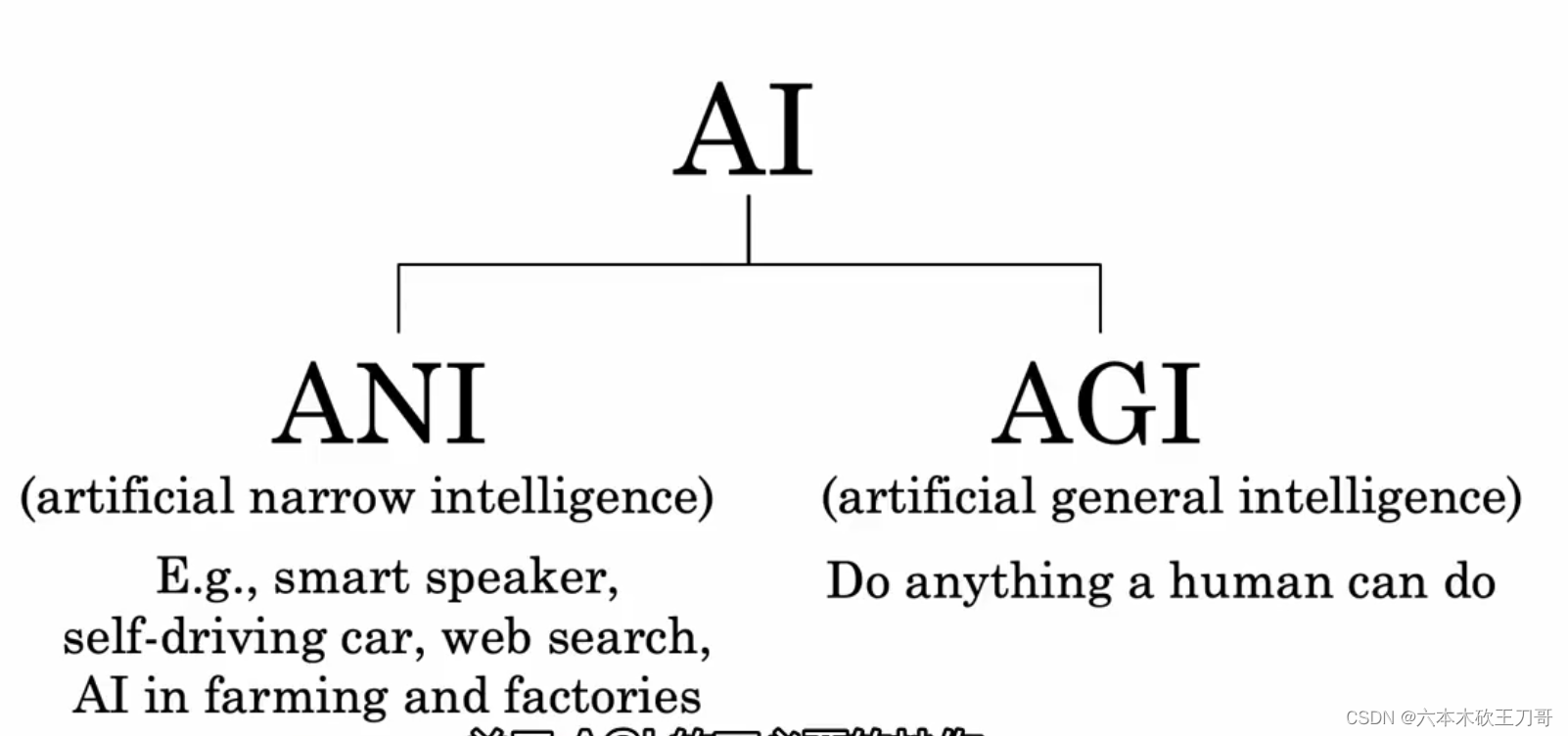
7.5 强人工智能
人工智能AI分为两大部分,ANI和AGI,其中ANI取得了巨大进步,但是AGI炒作过多。
目前无法实现AGI的最主要的原因是我们还不够了解大脑神经元的工作流程,并且逻辑回归所做的工作比起神经元还是太简单了。
但依然有很多有趣的生物实验...
7.6 神经网络为何如何高效
7.6.1 为何高效
神经网络高效的原因在于处理向量化处理,其中包括处理向量化矩阵乘法,下图中左边是原先的代码,它使用了for循环来处理每次计算,但是右边的代码首先将输入数组替换成了矩阵而不是原来的一维数组,然后使用了numpy的matmul函数直接进行矢量计算,提高了计算效率。
7.6.2 矩阵乘法
矩阵乘法的原理和matmul的实现
八、训练神经网络
之前实现了有关神经网络的推导,这部分主要是关注如何训练神经网络。
8.1 tensorflow实现和模型细节
首先使用tensorflow的相关库函数来实现。
第一步:指定模型如何计算和推理
第二步:编译模型,使用特定的损失函数(这里是交叉熵函数)
第三步:使用数据训练模型
以上的模型细节可以参考之前的最小化逻辑回归代价函数的步骤,第一步是指定模型,第二步是给出损失函数,第三步是用梯度下降法最小化代价函数,训练神经网络也是可以应用同样的理念,对应到代码中如下,第一步建立模型model,第二步指定损失函数为二元交叉熵函数,第三步调用fit来最小化模型误差。(迭代次数为100次)
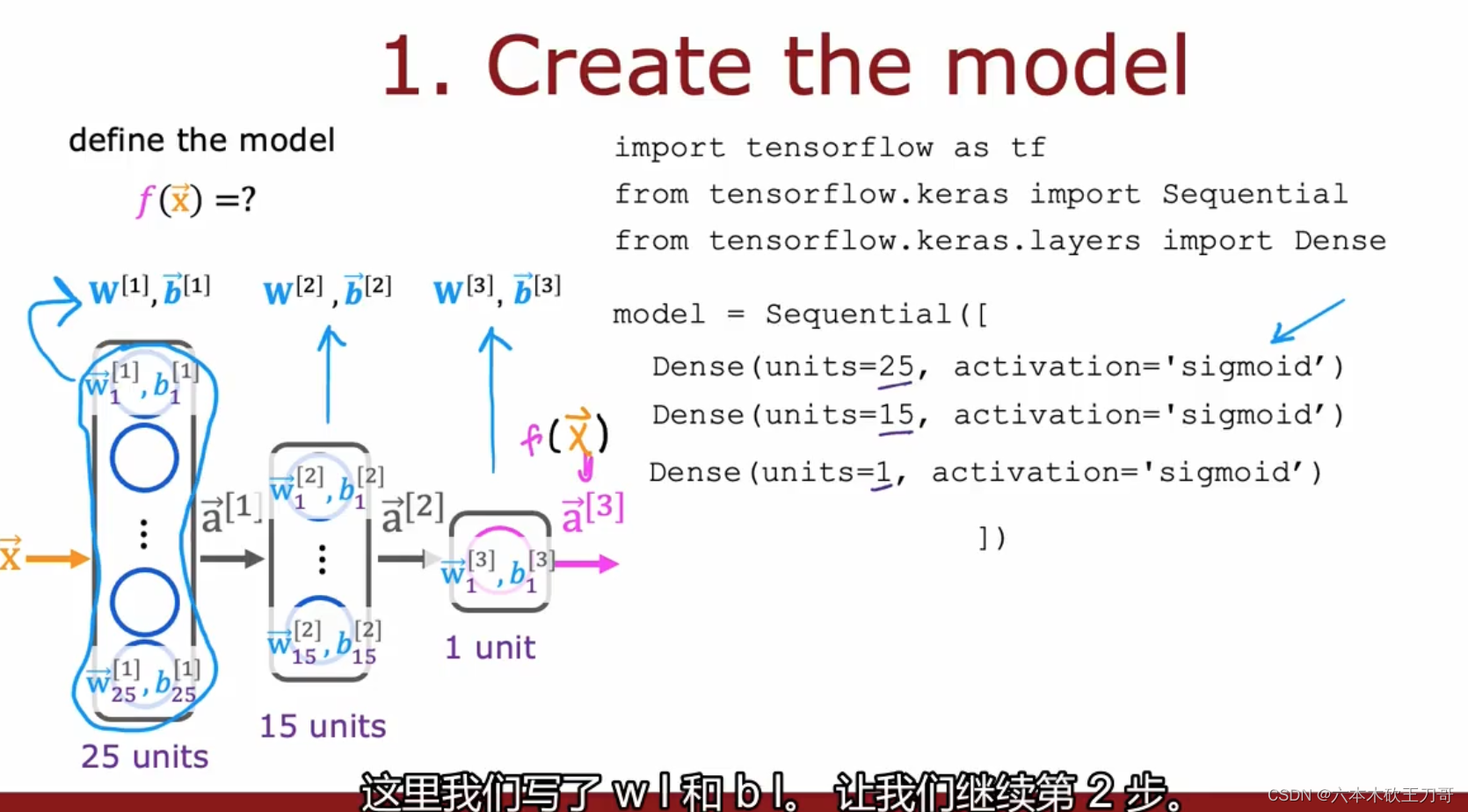
下图展示了第一步建立模型的细节。
第二步指定损失函数Binary Cross Entropy,其实在神经网络中,针对二元的分类问题,这个函数和之前逻辑回归的损失函数是同一个,使用这个函数来编译神经网络,它是源自Keras库,这个库最终被合并到了tensorflow中,我们从import的包中可以看得出来。当指定单个数据的损失函数之后,tensorflow知道我们要得到的数据是平均值,优化这个函数将使得模型fitting数据集的理论输出binary数据。
当然,如果我们是要训练回归问题,可以更改损失函数为均方误差函数。
第三步,最小化代价函数,在逻辑回归或者线性回归中,是同步更新所有w和b值来达到目的的,但是在神经网络的训练中,是使用反向传播算法来最小化代价函数。
当然,我们可以很简单的调用库函数来达到目的而不是从头开始写这个函数,但是深入了解背后的原理可以帮助我们在遇到问题的时候快速分析。
8.2 选择激活函数
8.2.1 Sigmoid的替代方案
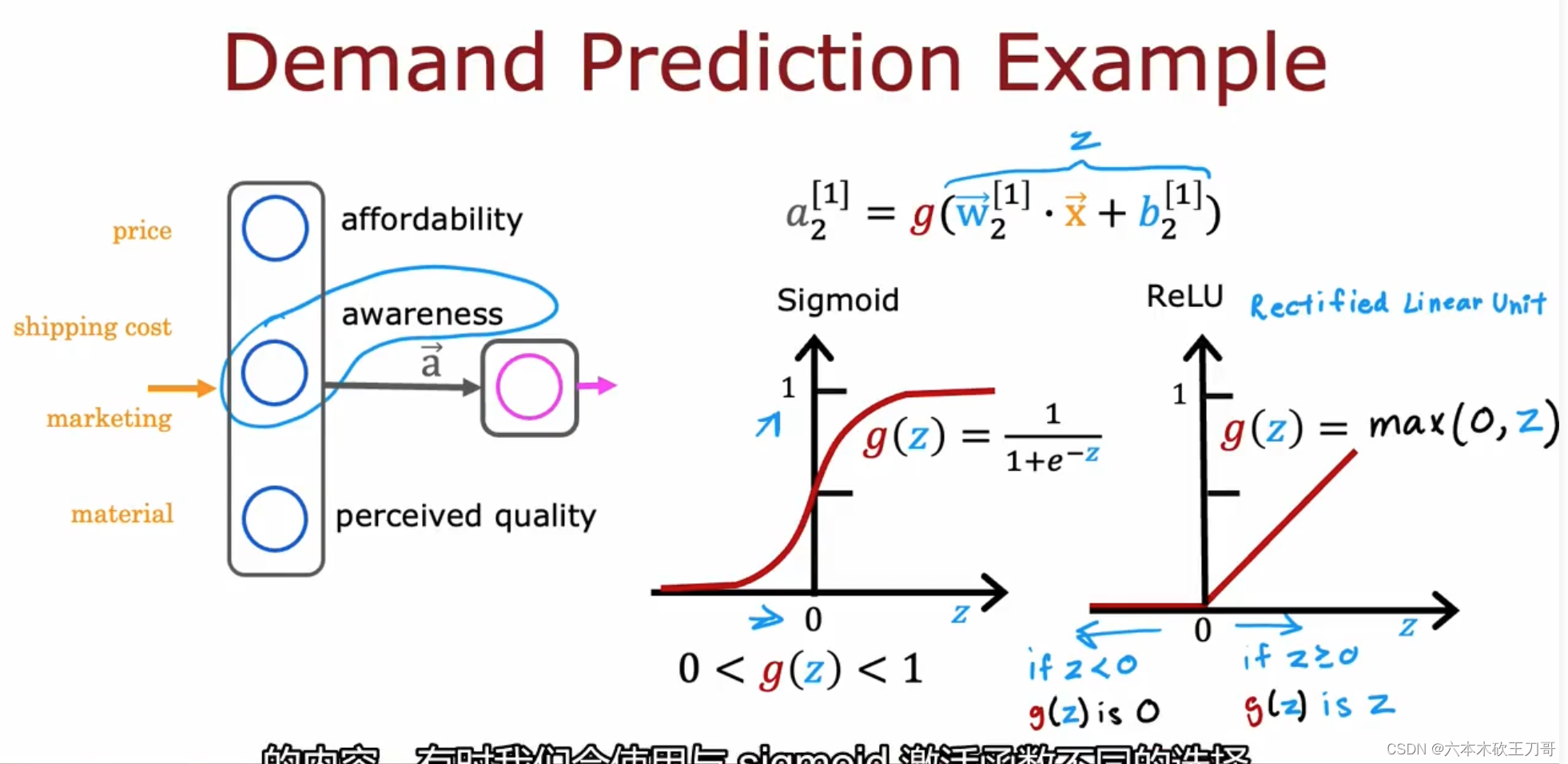
回想之前的需求模型,我们用0到1之间的小数字来得到每个单元的计算结果(之前每个单元用的是Sigmoid激活函数,它的输出是0或者1),但是有时候并不能说这样总是有效的,例如对某个商品的了解程度Awareness,可能不太了解,有点了解或者非常了解,这样就不能单纯用0和1来判断。
所以我们可以用ReLU激活函数(rectified linear function 整流线性单元)来替代,它在z小于0的时候为0,大于0的时候是一个线性函数,保证了输出值是大于等于0。
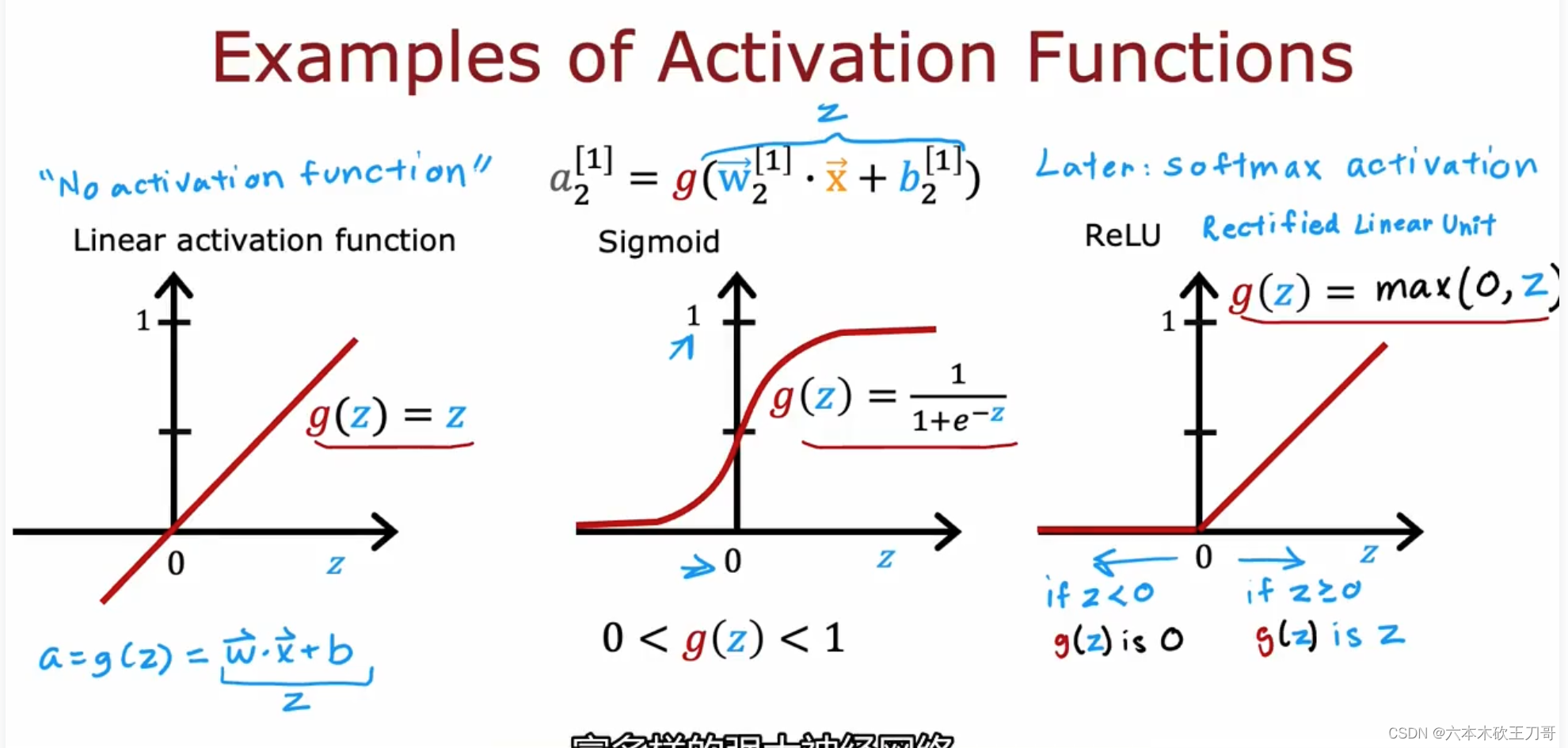
以下是目前为止最常用的三种激活函数:线性激活函数(有时候也被认为没有用到激活函数),Sigmoid激活函数,ReLU激活函数,之后还会介绍道Softmax函数。
8.2.2 如何选择激活函数
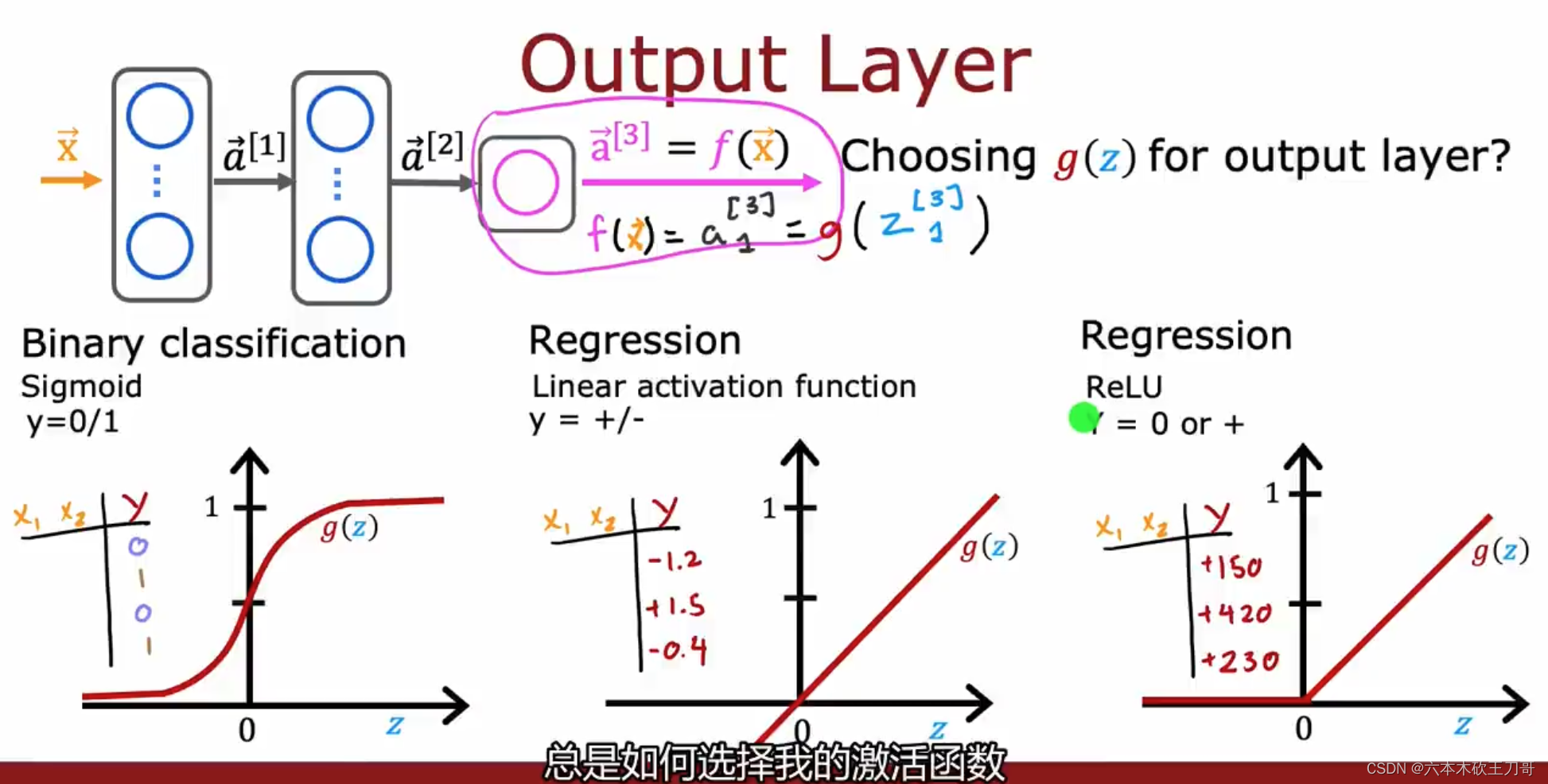
在输出层中如何选择激活函数取决于我们要解决的问题,如果是二元分类问题,通常是选择Sigmoid函数;如果是取值可正可负,例如股票预测问题,可以使用线性激活函数;如果是类似房价预测问题,输出只能是大于等于0的值,就可以使用ReLu激活函数。
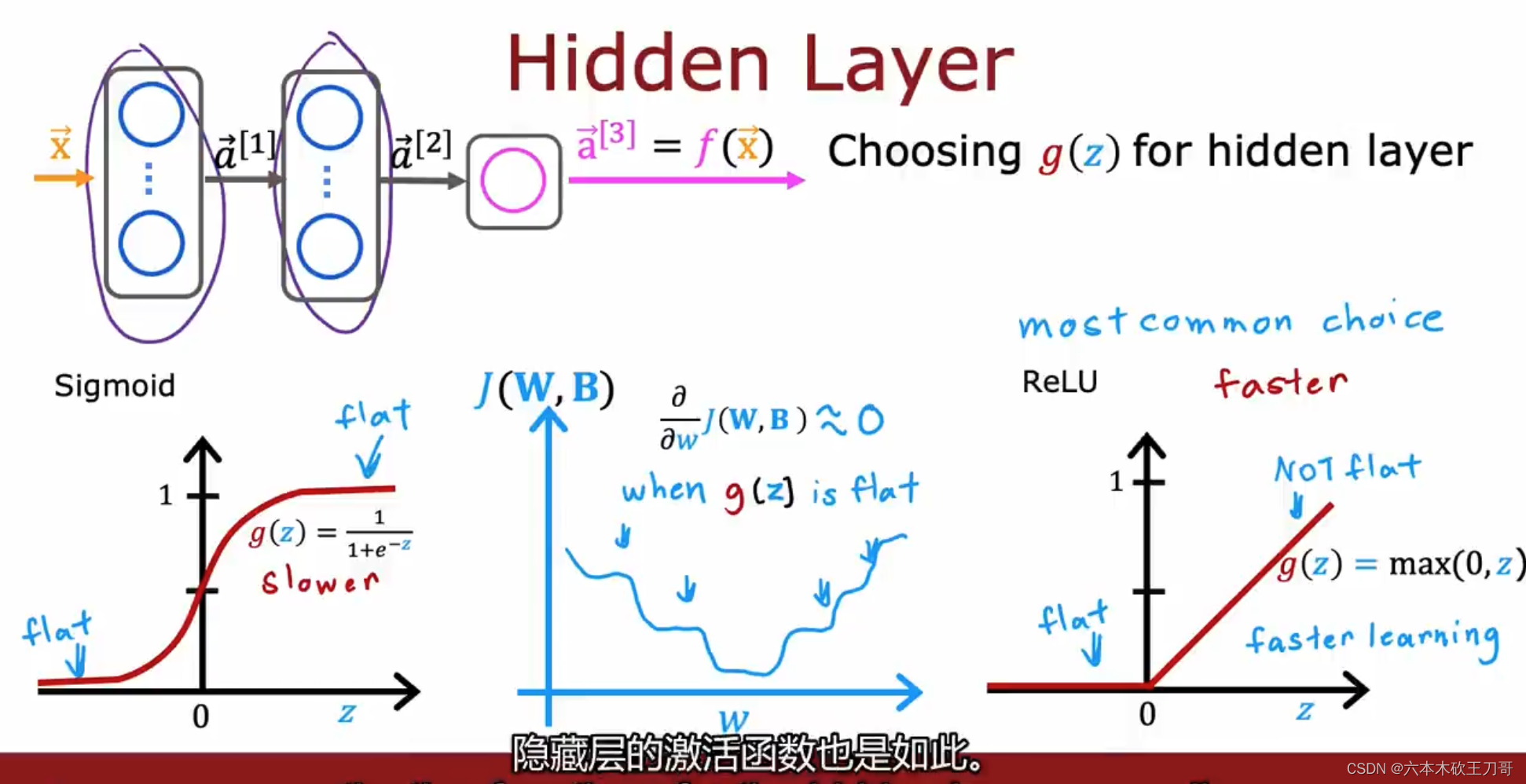
在隐藏层中,如果不是二元分类问题,很多情况下也都是使用ReLU函数来作为激活函数,主要原因有如下几个:
1.计算效率,一般ReLU函数计算更快,因为这是线性的,但是对于Sigmoid函数,需要计算指数
2.梯度下降收敛速度,对于Sigmoid函数,在函数图像两边是很平坦的, 所以有时候梯度下降速度会很慢,虽然我们知道优化的是代价函数而不是激活函数,但是激活函数是进入代价函数的基础,所以也会导致代价函数的某些部分变得平坦。
ReLU函数一般情况下会训练的更快。
当然,有时候也会用别的激活函数例如LeakeyReLU函数,但是大部分情况下以上三个函数基本足够使用。
8.2.3 为什么模型需要激活函数
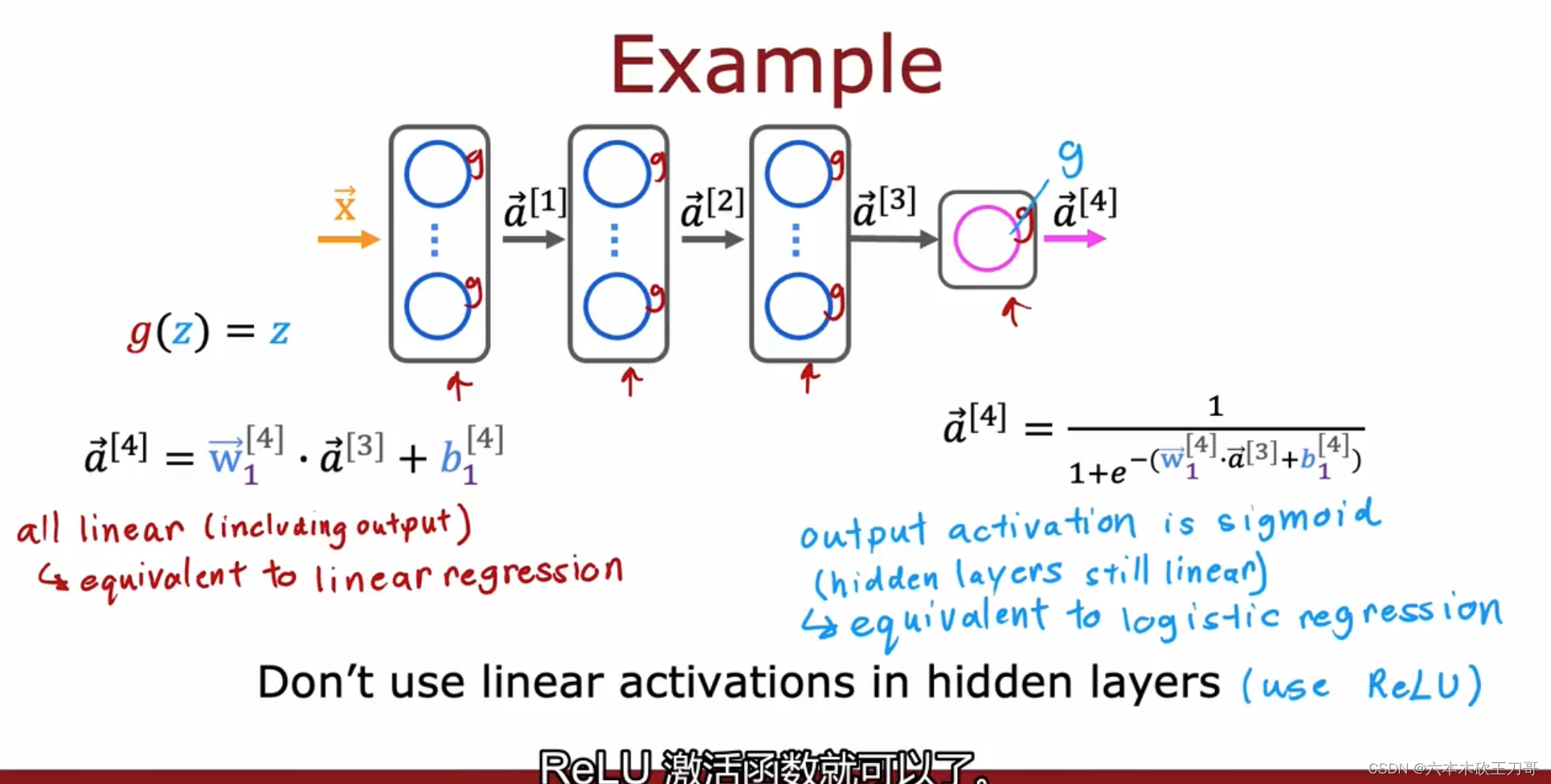
为什么需要激活函数而不是只使用线性激活或者干脆不使用?
因为只使用线性激活函数的话,等于隐藏层根本就没有作用了,因为线性函数输入线性函数的输出依旧是线性函数,即使当输出层是Sigmoid函数的时候, 隐藏层中间是线性函数,那么隐藏层的作用就不存在了。
8.3 多分类
当输出不再是二元分类,可以是多个分类输出值的时候,该如何推导?
8.3.1 多分类问题 Multi-class Classification Problem
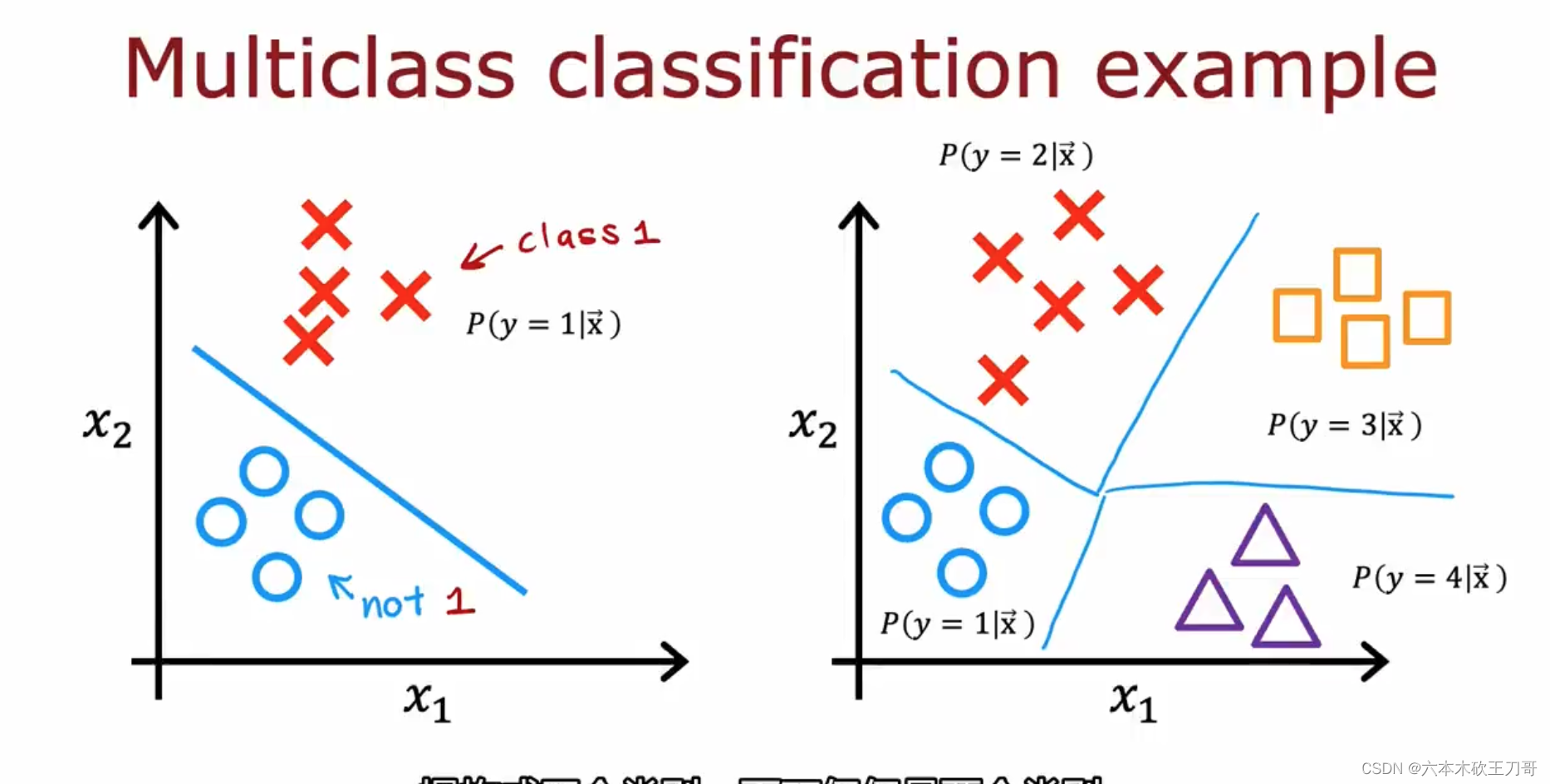
当我们有不止两种分类时(也就是𝑦 = 1,2,3 ....),比如以下这种情况,该怎么办? 例如识别的数字不仅限于0和1,而是全部十个数字。
这时候的分类问题也变成了具有多个输出值的问题,在下一节会用逻辑回归问题的推广,Softmax多分类问题来解决。
8.3.2 Softmax,输出和改进
softmax帮助我们预测和训练多分类问题
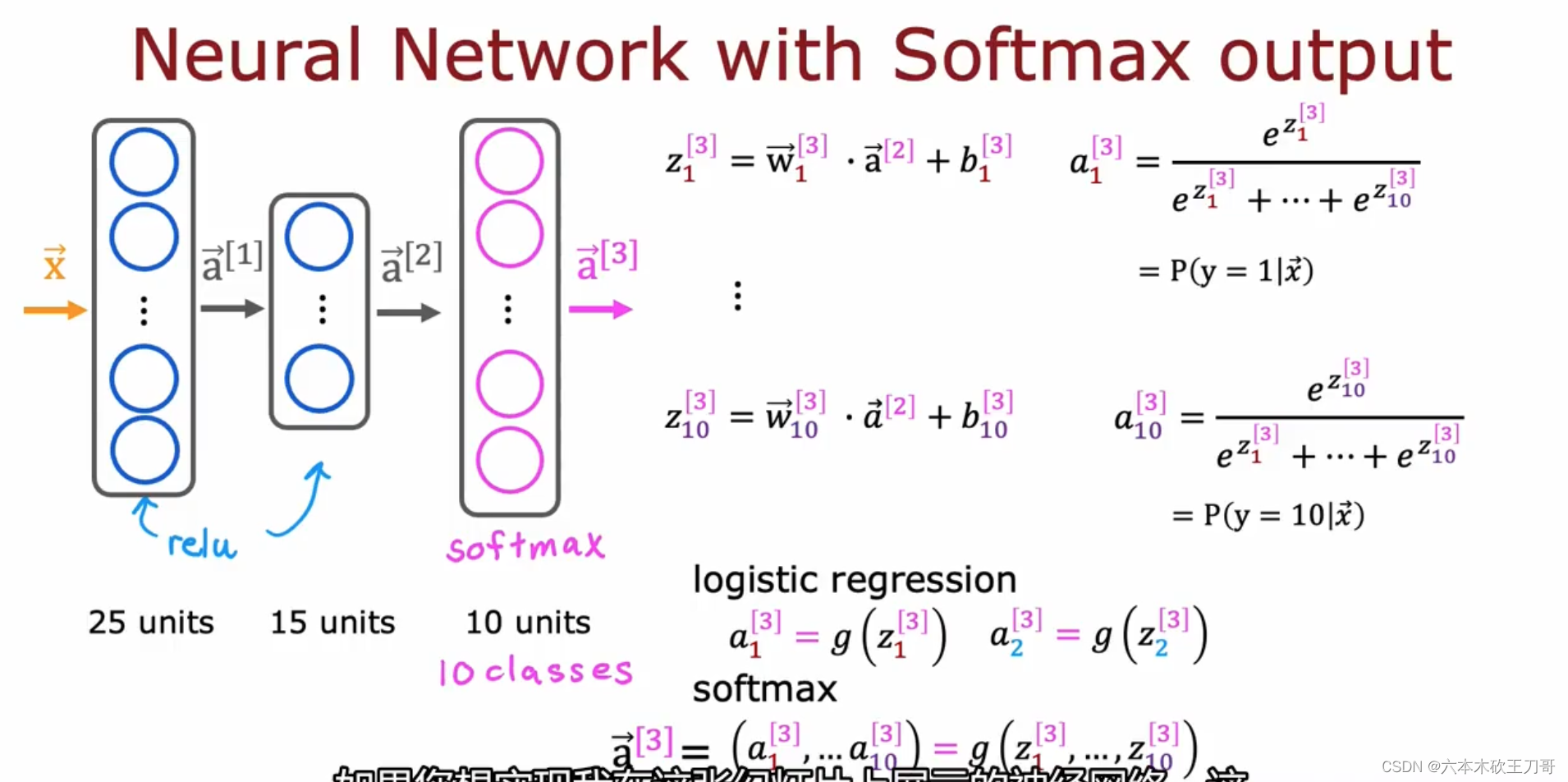
如何在神经网络上实现Softmax呢?可以把输出层设定为使用Softmax来作为激活函数,事实上,这一层的计算依旧是用w和b来计算z,但是当得到每一个输出Zn的时候,我们就需要通过这些Zn来计算输出的概率,也就是得到相应的a3输出。所以对于逻辑回归和softmax的区别在于,逻辑回归只需要当前计算单元的输出就可以直接代入Sigmoid函数得到输出,但是softmax是需要得到全部的计算Z值才能得到输出a3向量。
现在使用TensorFlow来实现代码。
与之前的代码类似,也是分为三部分,区别在于第一步中建立model中输出层的激活函数需要使用softmax,第二步中的损失函数需要使用SparseCategoricalCrossentropy函数,这是用于多分类问题的函数,Sparse和Category代表了输出值是离散值的分类问题(例如数字识别0 1 2 3 ... 的分类问题),第三步需要训练模型。但是这段代码并不推荐使用。
可以进一步改进实现
8.3.3 多个输出的分类 Multi-label Classification Problem
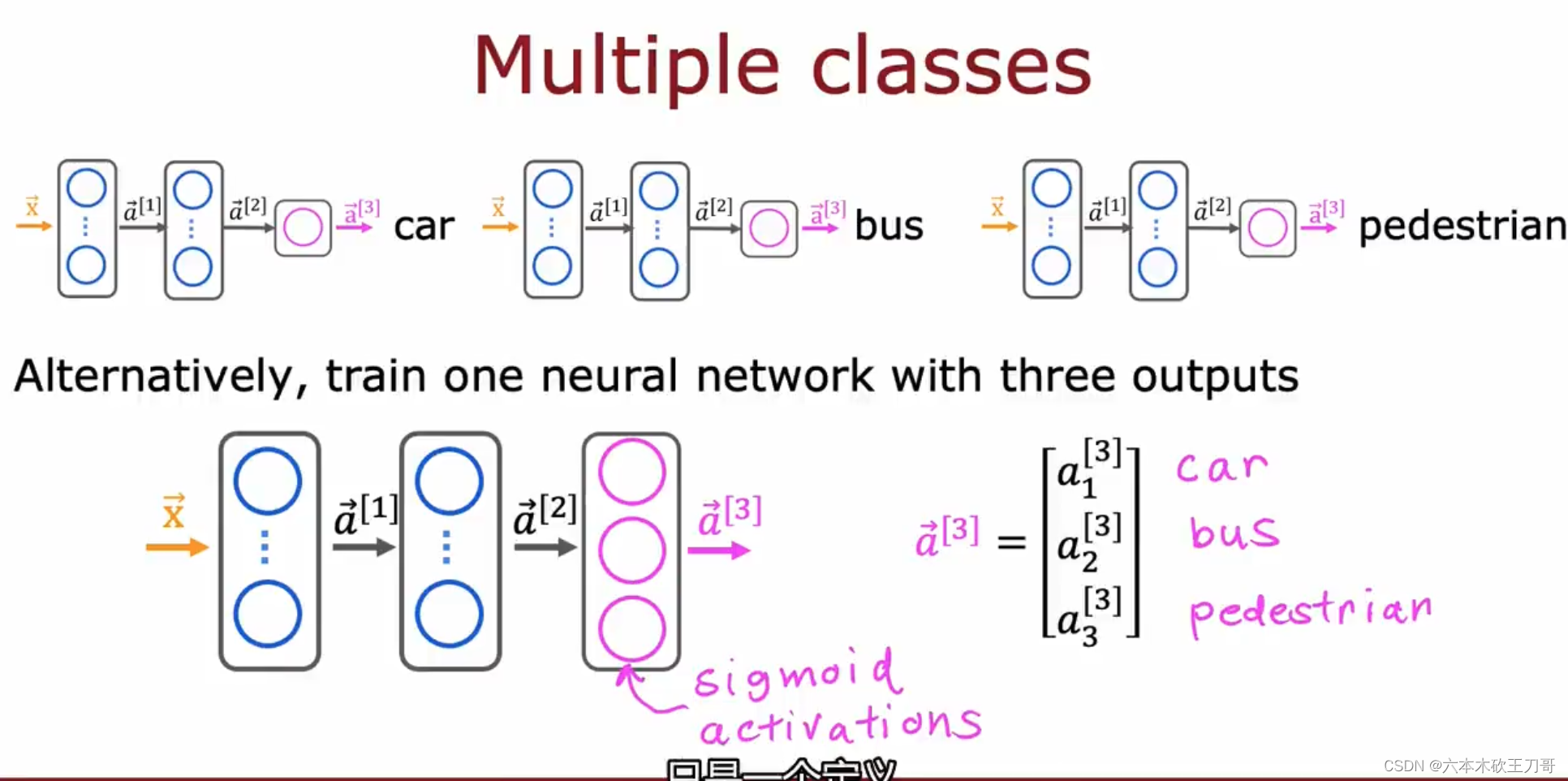
对于数字识别问题,是属于multi-class问题,给出的输出值是属于某一类,但是多标签问题,输出不仅仅只属于某一类,而是包含了多个标签,例如下图的图像识别问题, 需要识别三种物体:car,bus,pedestrian,所以输出是一个向量。
或许可以使用三个网络来解决这个问题,每个网络负责识别其中一种物体,但是这个太麻烦,我们依旧可以用一个网络来解决这个问题,实际上这是一个三组二分类问题,也就是说输出层可以是三个Sigmoid单元,这样每个单元输出0或者1,等同于判断是否存在这个物体。
主要目的是不要混淆多分类和多标签问题。
8.4 高级优化方法
8.4.1 高级优化
梯度下降是线性回归,逻辑回归和早期神经网络训练的主要方法。
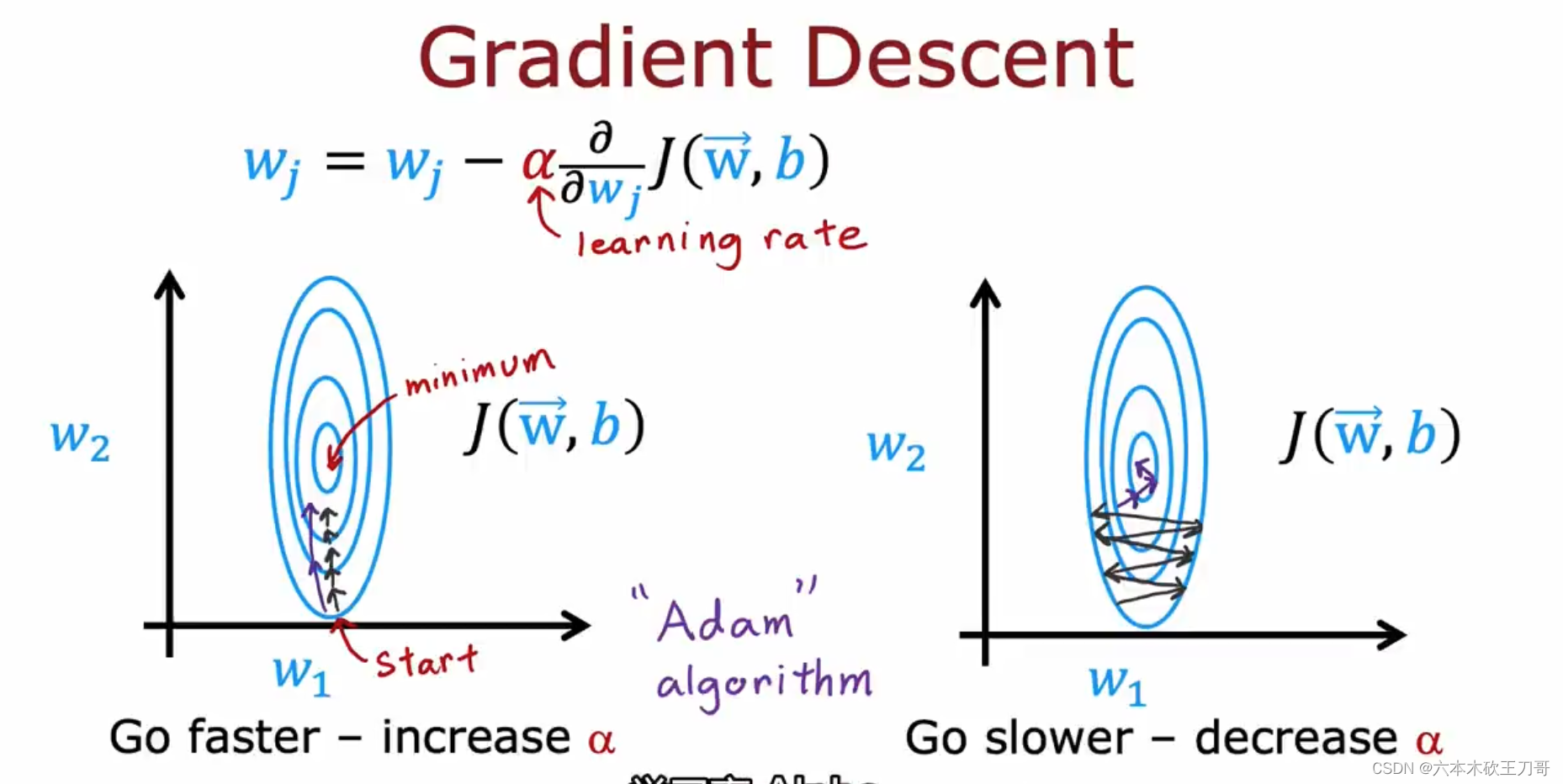
在梯度下降中,低的学习率可能会导致收敛的步长太小,需要花费很多步才能到达最小值点,使用Adam算法可以调整学习率来帮助加快收敛速度。
Adam的全名是Adaptive Moment estimation,它不仅仅只采用一个学习率修改,它会同时改变全部参数的学习率。
对Adam更直观的理解是,如果需要更快的收敛,就可以增加学习率,如果收敛过程来回震荡,就可以降低学习率,Adam算法的细节超出了本课程的范围。
代码中需要注意的是,在编译模型的时候,需要加上Adam的优化参数并设置初始学习率。
8.4.2 其他网络层类型
本小节探讨除了dense layer外的其他网络层类型。
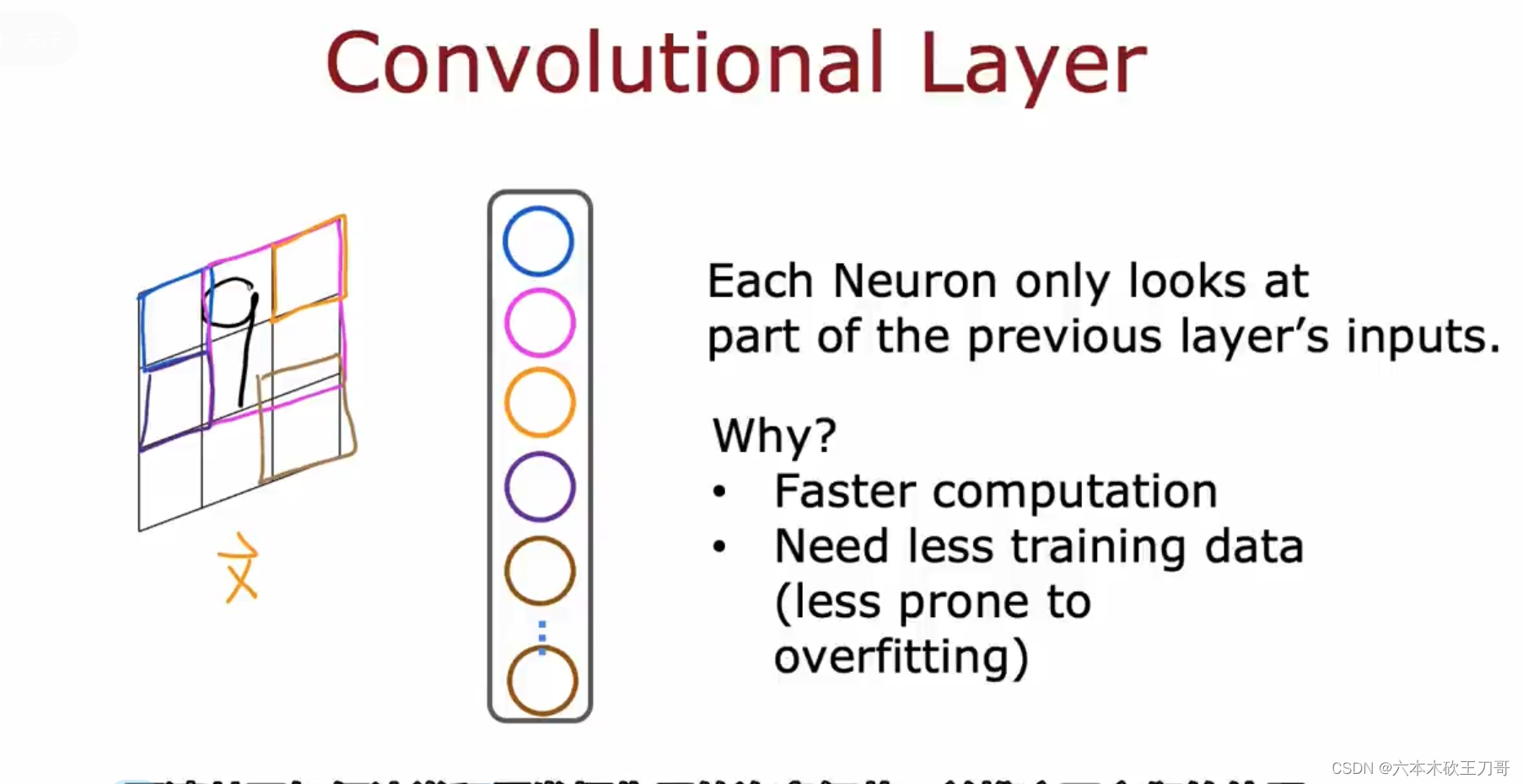
例如卷积层,它的输入不再是整个数据集,而是数据集的一部分,下图中的图像输入,卷积层的每个计算单元只接收图像某一个部分的数据输入,这样做的原因是可以帮助更快速的计算,和防止过拟合(这个之后还会介绍)。
下面是卷积神经网络的一些细节。用一个心电图的案例来说明,假设横坐标有1到100个数据,纵坐标是心电图的高度,我们要通过这组数据来训练神经网络,如果此时用卷积神经网络,那么输入的数据集将会被分割,例如第一个卷积层有9个计算单元,那么每个计算单元交叉的分到20个数据集,然后第二个卷积层有3个计算单元,它们接受上一个卷积层的输出,依然从9个输出中分割数据,最后经过一个Sigmoid层得到输出。
现在,除了卷积神经网络,还出现了更多更复杂的网络,例如transformer,LSTM等注意力模型,使用不同的网络层组成不同的结构,可以发挥更多的作用。
8.5 导数,计算图和大型神经网络(optional)
如果增加一个很小的值


计算图
一个线性单元计算图的例子
九、应用机器学习的建议
9.1 决定下一步做什么
9.1.1 下一步做什么
到目前为止,我们已经介绍了许多不同的学习算法,如果你一直跟着这些视频的进度学习,你会发现自己已经不知不觉地成为一个了解许多先进机器学习技术的专家了。
然而,在懂机器学习的人当中依然存在着很大的差距,一部分人确实掌握了怎样高效 有力地运用这些学习算法。而另一些人他们可能对我马上要讲的东西,就不是那么熟悉了。 他们可能没有完全理解怎样运用这些算法。因此总是把时间浪费在毫无意义的尝试上。我想 做的是确保你在设计机器学习的系统时,你能够明白怎样选择一条最合适、最正确的道路。 因此,在这节视频和之后的几段视频中,我将向你介绍一些实用的建议和指导,帮助你明白 怎样进行选择。具体来讲,我将重点关注的问题是假如你在开发一个机器学习系统,或者想 试着改进一个机器学习系统的性能,你应如何决定接下来应该选择哪条道路?为了解释这一 问题,我想仍然使用预测房价的学习例子,假如你已经完成了正则化线性回归,也就是最小 化代价函数𝐽的值,假如,在你得到你的学习参数以后,如果你要将你的假设函数放到一组 新的房屋样本上进行测试,假如说你发现在预测房价时产生了巨大的误差,现在你的问题是 要想改进这个算法,接下来应该怎么办?
实际上你可以想出很多种方法来改进这个算法的性能,其中一种办法是使用更多的训 练样本。具体来讲,也许你能想到通过电话调查或上门调查来获取更多的不同的房屋出售数 据。遗憾的是,我看到好多人花费了好多时间想收集更多的训练样本。他们总认为,要是我 有两倍甚至十倍数量的训练数据,那就一定会解决问题的是吧?但有时候获得更多的训练数 据实际上并没有作用。在接下来的几段视频中,我们将解释原因。
我们也将知道怎样避免把过多的时间浪费在收集更多的训练数据上,这实际上是于事无补的。另一个方法,你也许能想到的是尝试选用更少的特征集。因此如果你有一系列特征比如𝑥1, 𝑥2, 𝑥3等等。也许有很多特征,也许你可以花一点时间从这些特征中仔细挑选一小部分来防止过拟合。或者也许你需要用更多的特征,也许目前的特征集,对你来讲并不是很有 帮助。你希望从获取更多特征的角度来收集更多的数据,同样地,你可以把这个问题扩展为 一个很大的项目,比如使用电话调查来得到更多的房屋案例,或者再进行土地测量来获得更 多有关,这块土地的信息等等,因此这是一个复杂的问题。同样的道理,我们非常希望在花 费大量时间完成这些工作之前,我们就能知道其效果如何。我们也可以尝试增加多项式特征 的方法,比如𝑥1的平方,𝑥2的平方,𝑥1, 𝑥2的乘积,我们可以花很多时间来考虑这一方法,我 们也可以考虑其他方法减小或增大正则化参数𝜆的值。我们列出的这个单子,上面的很多方 法都可以扩展开来扩展成一个六个月或更长时间的项目。遗憾的是,大多数人用来选择这些 方法的标准是凭感觉的,也就是说,大多数人的选择方法是随便从这些方法中选择一种,比 如他们会说“噢,我们来多找点数据吧”,然后花上六个月的时间收集了一大堆数据,然后也 许另一个人说:“好吧,让我们来从这些房子的数据中多找点特征吧”。我很遗憾不止一次地 看到很多人花了至少六个月时间来完成他们随便选择的一种方法,而在六个月或者更长时间 后,他们很遗憾地发现自己选择的是一条不归路。
幸运的是,有一系列简单的方法能让你事 半功倍,排除掉单子上的至少一半的方法,留下那些确实有前途的方法,同时也有一种很简 单的方法,只要你使用,就能很轻松地排除掉很多选择,从而为你节省大量不必要花费的时 间。最终达到改进机器学习系统性能的目的假设我们需要用一个线性回归模型来预测房价, 当我们运用训练好了的模型来预测未知数据的时候发现有较大的误差,我们下一步可以做什么?
获得更多的训练实例——通常是有效的,但代价较大,下面的方法也可能有效,可考虑 先采用下面的几种方法。
1.尝试减少特征的数量
2.尝试获得更多的特征
3.尝试增加多项式特征
4.尝试减少正则化程度𝜆
5.尝试增加正则化程度𝜆
我们不应该随机选择上面的某种方法来改进我们的算法,而是运用一些机器学习诊断法来帮助我们知道上面哪些方法对我们的算法是有效的。
首先介绍怎样评估机器学习算法的性能,然后在之后的几段视频中,将开始讨论这些方法,它们也被称为"机器学习诊断法"。“诊断法”的意思是:这是一种测试法,你通过执行这种测试,能够深入了解某种算法到底是否有用。这通常也能够 告诉你,要想改进一种算法的效果,什么样的尝试,才是有意义的。在这一系列的视频中我 们将介绍具体的诊断法,但我要提前说明一点的是,这些诊断法的执行和实现,是需要花些时间的,有时候确实需要花很多时间来理解和实现,但这样做的确是把时间用在了刀刃上, 因为这些方法让你在开发学习算法时,节省了几个月的时间,因此,在接下来几节课中,我 将先来介绍如何评价你的学习算法。
在此之后,我将介绍一些诊断法,希望能让你更清楚。在接下来的尝试中,如何选择更有意义的方法。
9.1.2 模型评估
当我们确定学习算法的参数的时候,我们考虑的是选择参量来使训练误差最小化,有人 认为得到一个非常小的训练误差一定是一件好事,但我们已经知道,仅仅是因为这个假设具有很小的训练误差,并不能说明它就一定是一个好的假设函数。而且我们也学习了过拟合假设函数的例子,所以这推广到新的训练集上是不适用的。
继续参考以下房屋预测模型,当我们输入特征只有size的时候,绘制了图像,并拟合训练数据,但是这可能会带来过拟合的问题。
那么,你该如何判断一个假设函数是过拟合的呢?对于这个简单的例子,我们可以对假设函数f(𝑥)进行画图,然后观察图形趋势,但对于特征变量不止一个的这种一般情况,还有像有很多特征变量的问题,想要通过画出假设函数来进行观察,就会变得很难甚至是不可能实现。
因此,我们需要另一种方法来评估我们的假设函数过拟合检验。
为了检验算法是否过拟合,我们将数据分成训练集和测试集,通常用 70%的数据作为训练集,用剩下 30%的数据作为测试集。很重要的一点是训练集和测试集均要含有各种类型的数据,通常我们要对数据进行“洗牌”,然后再分成训练集和测试集。
测试集评估在通过训练集让我们的模型学习得出其参数后,对测试集运用该模型,我们有两种方式计算误差:
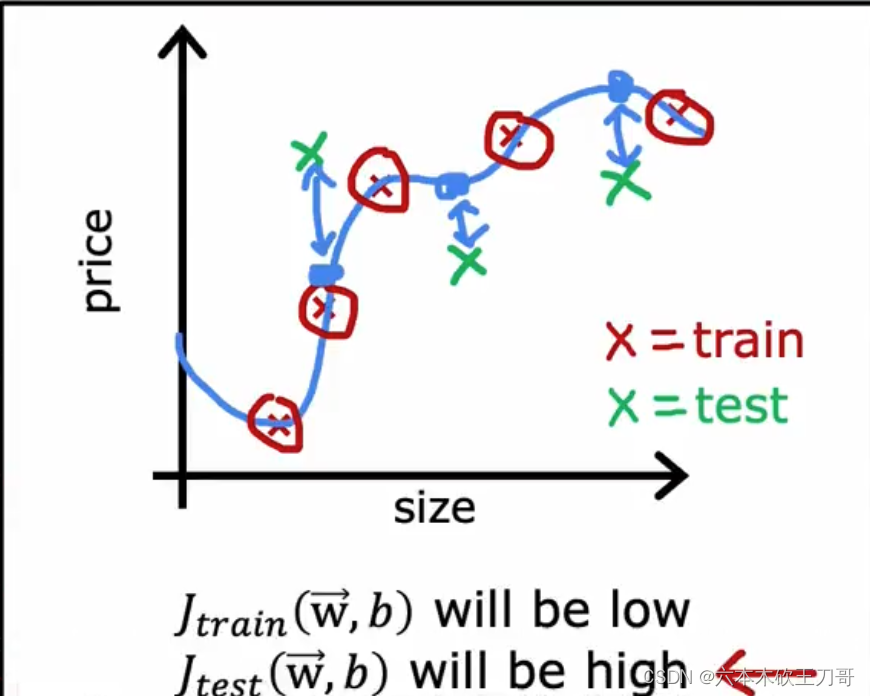
1.对于线性回归模型,我们利用测试集数据计算代价函数𝐽 train,然后用测试集来计算测试误差
如果训练结果如下图,说明训练集拟合的比较好,但是测试集的误差比较大。
2.对于逻辑回归模型,我们可以利用测试数据集来计算代价函数。
除了使用损失函数和代价函数的误差来判定之外,还可以使用训练集和测试集中错误分类的比例来评估模型。
9.1.3 模型选择和交叉验证测试集的训练方法
如何通过测试集来选择更好的模型?
假设我们要在 10 个不同次数的二项式模型之间进行选择。
显然越高次数的多项式模型越能够适应我们的训练数据集,但是适应训练数据集并不代表着能推广至一般情况,我们应该选择一个更能适应一般情况的模型。我们需要使用交叉验证集来帮助选择模型。
即:使用 60%的数据作为训练集,使用 20%的数据作为交叉验证集,使用 20%的数据作为测试集
模型选择的方法为:
1. 使用训练集训练出 10 个模型
2. 用 10 个模型分别对交叉验证集计算得出交叉验证误差(代价函数的值)
3. 选取代价函数值最小的模型
4. 用步骤 3 中选出的模型对测试集计算得出推广generalization误差(代价函数的值)
可以继续用下面的代价函数来计算误差。
用交叉验证集来选择模型,假设4阶的函数误差最小。注意到没有拟合,所以测试集表现出更好的泛化误差?(这里不太理解)
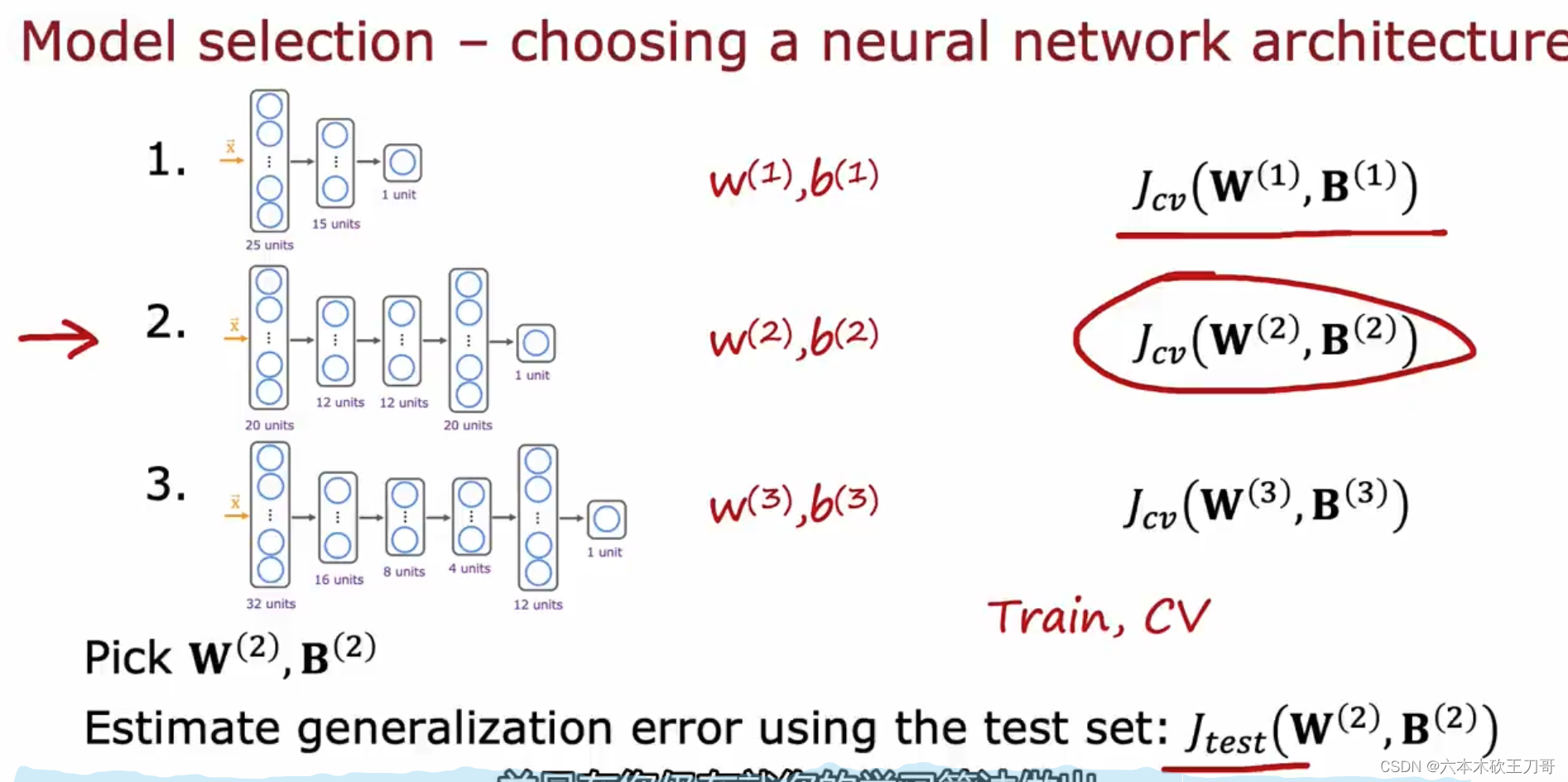
可以用同样的方法应用到别的模型中,例如神经网络。
同样的步骤也可以应用于神经网络选择。为了让测试集不unfair,需要通过交叉验证集来选择模型,最后再用测试集来计算泛化误差。
9.2 诊断模型
9.2.1 通过偏差和方差来诊断模型
当你运行一个学习算法时,如果这个算法的表现不理想,那么多半是出现两种情况: 要么是偏差比较大,要么是方差比较大。换句话说,出现的情况要么是欠拟合,要么是过拟 合问题。那么这两种情况,哪个和偏差有关,哪个和方差有关,或者是不是和两个都有关? 搞清楚这一点非常重要,因为能判断出现的情况是这两种情况中的哪一种。其实是一个很有效的指示器,指引着可以改进算法的最有效的方法和途径。在这段视频中,我想更深入地探 讨一下有关偏差和方差的问题,希望你能对它们有一个更深入的理解,并且也能弄清楚怎样 评价一个学习算法,能够判断一个算法是偏差还是方差有问题,因为这个问题对于弄清如何 改进学习算法的效果非常重要,高偏差和高方差的问题基本上来说是欠拟合和过拟合的问题。
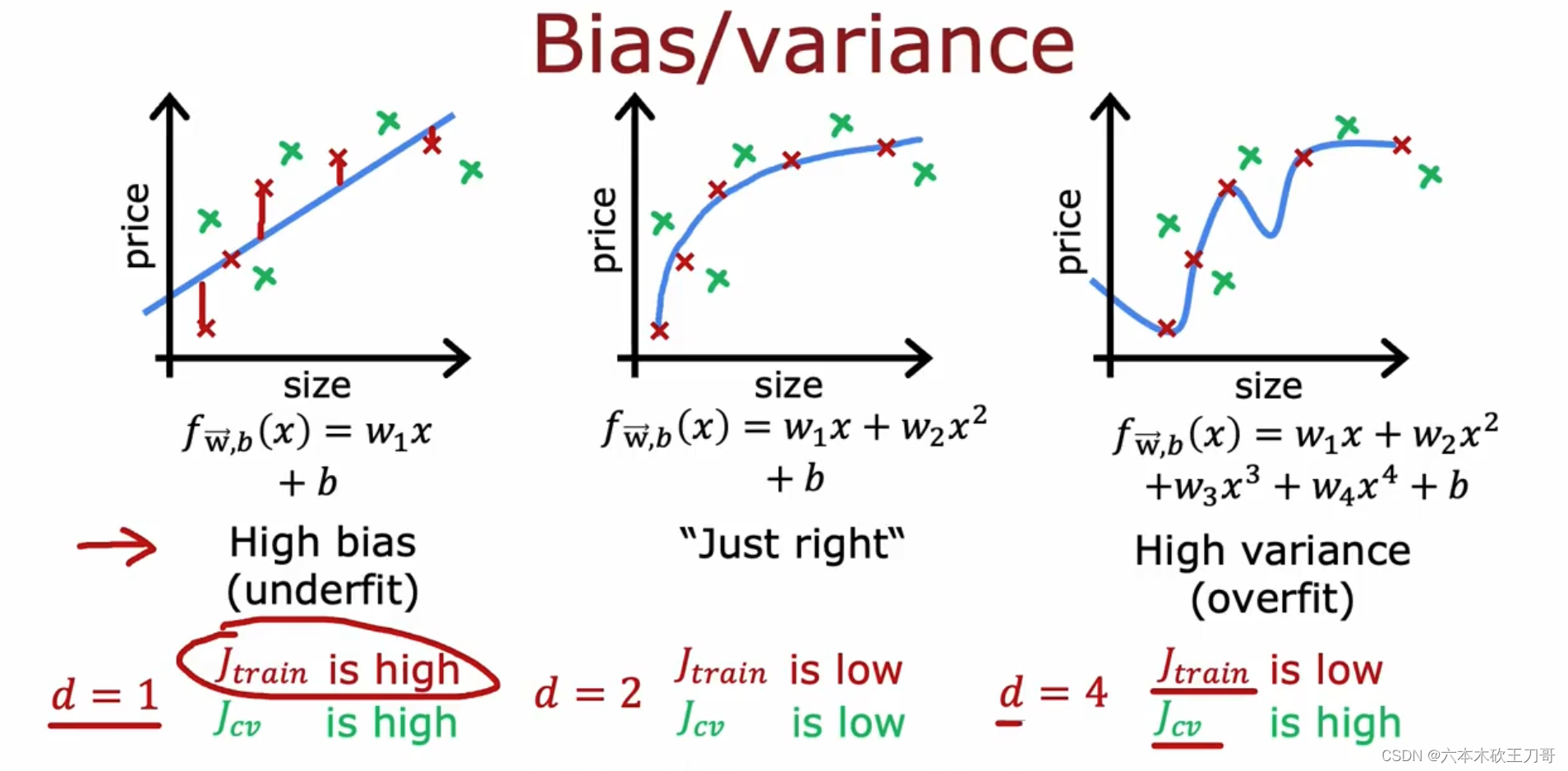
下图中的一次直线代表了训练集误差和验证集误差都较高,说明bias较高;第二个图两个误差都很低,说明偏差和方差都很低;第三个图是过拟合,训练集误差较低但是验证集误差较高,说明它的方差较高。
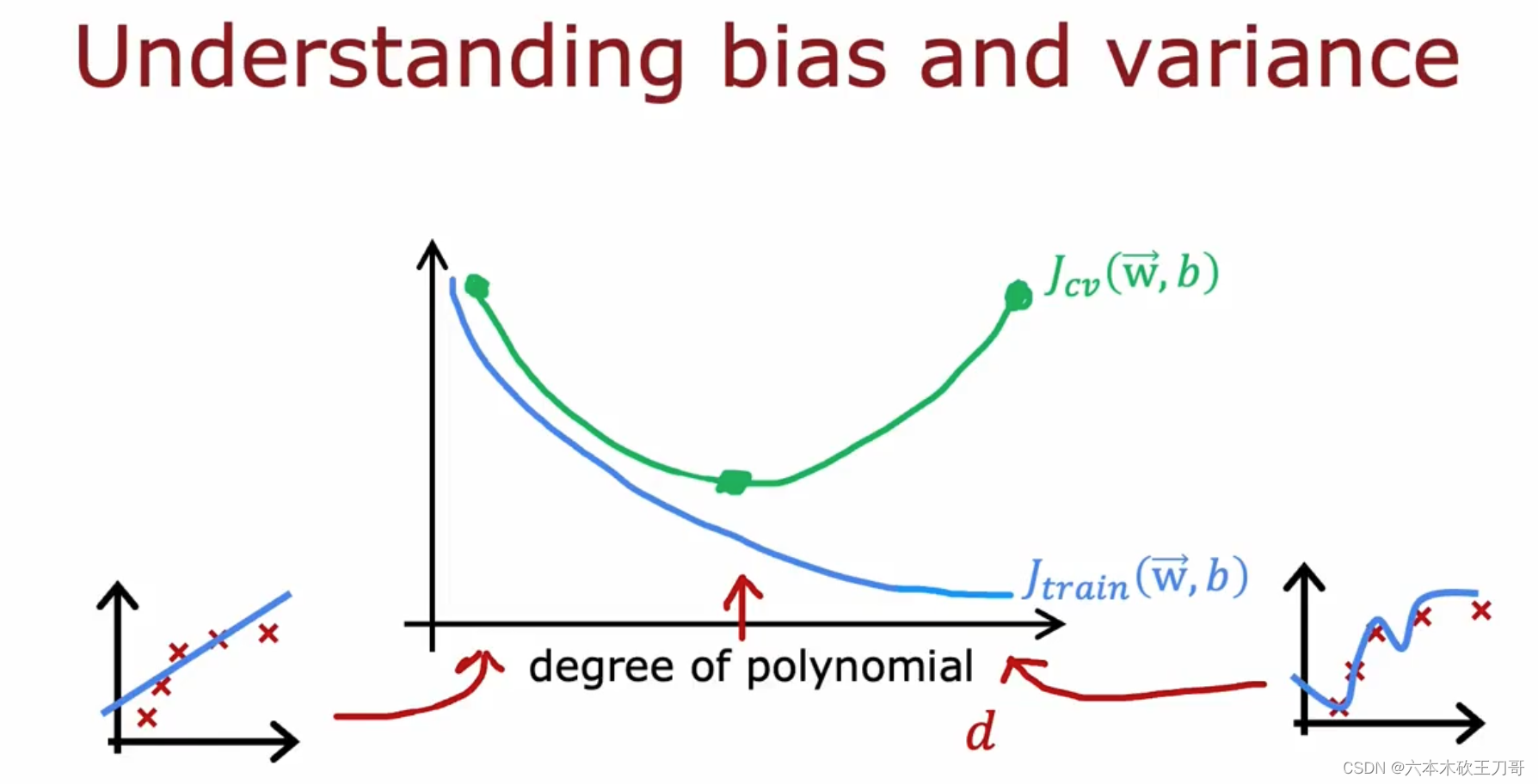
我们通常会通过将训练集和交叉验证集的代价函数误差与多项式的次数(上图中是1,2,4)绘制在同一张图表上来帮助分析。训练集的误差会根据多项式的次数增加而减小,这是因为一般来说线性函数拟合数据的效果不太理想(欠拟合),随着多项式次数增加,J train会下降,拟合的效果会越来越好。但是如果过大导致过拟合,那么会导致验证集的误差J cv变大,或者是过小欠拟合,也会导致验证集误差过大,只有当出现中间的多项式时(这个例子中时二次方程),方差和偏差都不会大。
如何诊断模型的偏差和方差?下图解释了对应的情况,前两种情况分别是高偏差(欠拟合)和高方差(过拟合)。
训练集误差和交叉验证集误差近似时:偏差/欠拟合
交叉验证集误差远大于训练集误差时:方差/过拟合
第三种情况时高偏差和高方差同时存在,这个也是有可能出现的,对应图中时一部分数据过拟合,另一部分数据是欠拟合,所以同时带来两个问题。
9.2.2 正则化,偏差和方差
在我们在训练模型的过程中,一般会使用一些正则化方法来防止过拟合。但是我们可能会正则化的程度太高或太小了,即我们在选择 λ 的值时也需要思考与刚才选择多项式模型次数类似的问题。
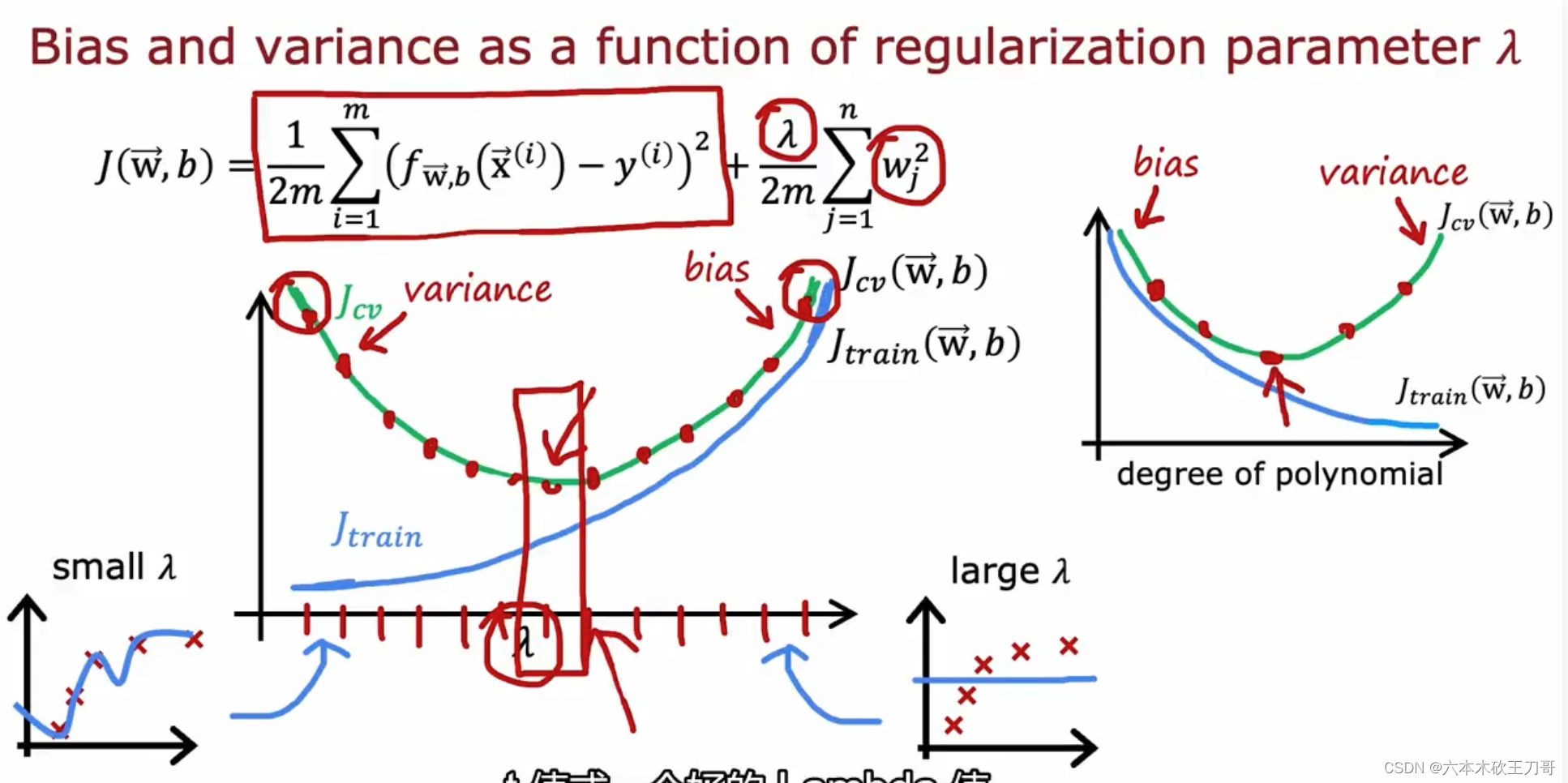
下图展示了三组选择不同λ的效果,第一个图是选择极大的λ,导致了拟合出来的函数几乎于横轴平行,因为如果是过大的λ,为了让代价函数J的值减小,只能让wj变小,这会导致wj的选择皆接近为0,导致f(x)的系数都为0从而变成f(x)=b。
第三个图是另一种极端情况,它选择了 λ = 0,这会导致正则化项直接消失,从而导致没有正则化而过拟合。
所以如何选择 λ 的值?我们可以选择一系列的想要测试的 𝜆 值,通常是 0-10 之间的呈现 2 倍关系的值(如: 0,0.01,0.02,0.04,0.08,0.15,0.32,0.64,1.28,2.56,5.12,10共12 个)。我们同样把数据分为训练集、交叉验证集和测试集。 例如下图中,建立12个模型,选择其中
选择𝜆的方法为:
1.使用训练集训练出 12 个不同程度正则化的模型
2.用 12 个模型分别对交叉验证集计算的出交叉验证误差
3.选择得出交叉验证误差最小的模型
4.运用步骤 3 中选出模型对测试集计算得出推广误差。
我们也可以同时将训练集和交叉验证集模型的代价函数误差与 λ 的值绘制在一张图表上,随着λ的变化,J train和 J cv会改变,也就是出现不同的高偏差和高方差情况。
• 当 𝜆 较小时,训练集误差较小(过拟合)而交叉验证集误差较大
• 随着 𝜆 的增加,训练集误差不断增加(欠拟合),而交叉验证集误差则是先减小后增加
9.2.3 制定一个用于性能评估的基准
拿语音识别举例,通过比较训练集的误差和验证集的误差,我们认为这个误差可能不低,但是如果说给出一个比较的基准,例如人类的水平也只能达到10.6%,其实训练集表现的性能已经很好了,这是由于某些语音里可能带来一些噪音,导致人类也无法真正的识别,所以也就可以容忍机器的性能。
下面举了一些可以作为基准的例子。
基于以上基准,我们需要对自己的算法做出一些评价,如果训练集的误差和我们期望的基准误差相差较小,可以认为没有偏差,如果验证集的误差和训练误差相差较大,就可以认为存在较大的方差,如果这这三者相差都很大,那么就有高偏差和高方差。
9.2.4 学习曲线 Learning Curve
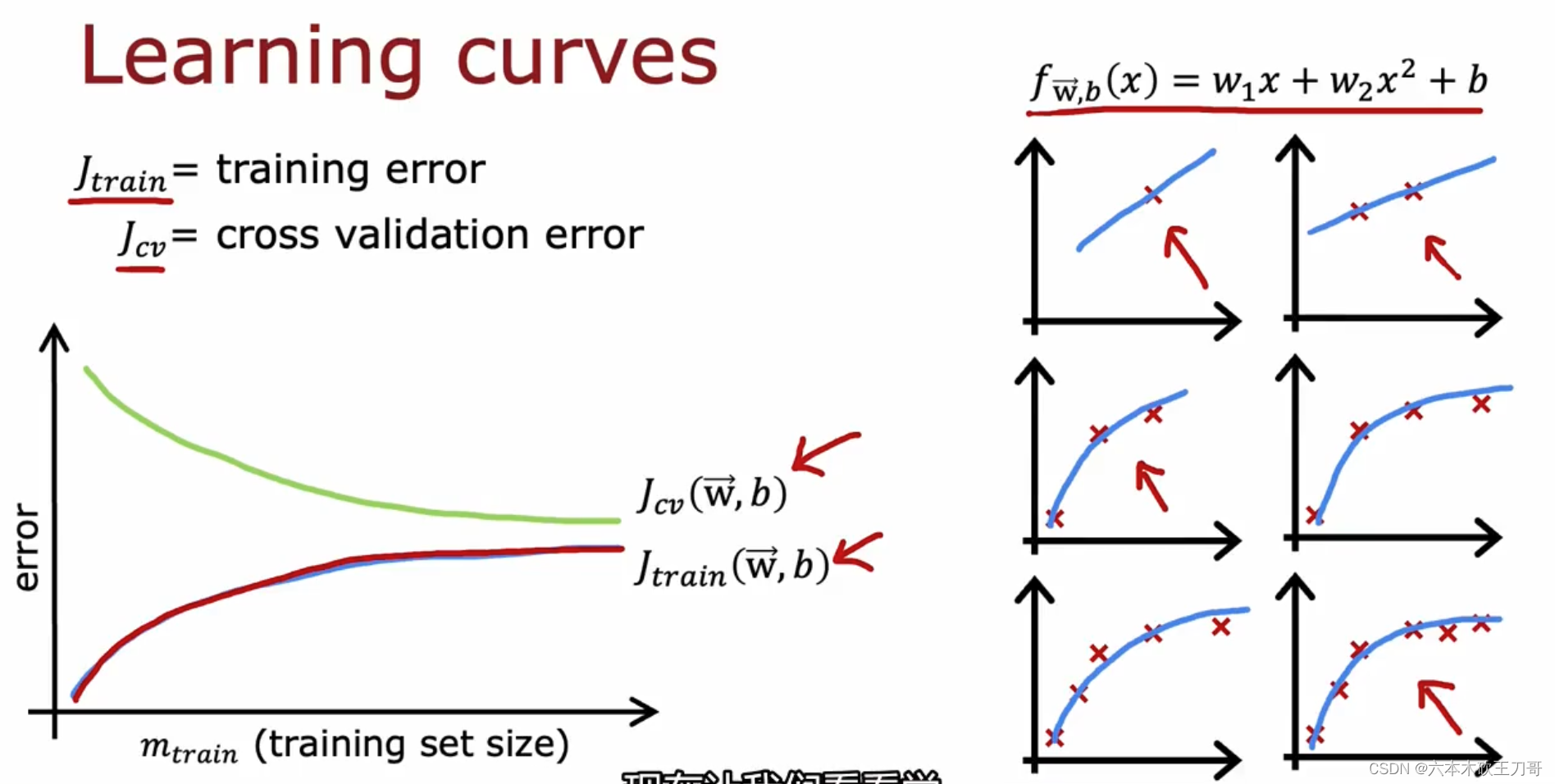
学习曲线就是一种很好的工具,我经常使用学习曲线来判断某一个学习算法是否处于偏 差、方差问题。学习曲线是学习算法的一个很好的合理检验(sanity check)。学习曲线是将训练集误差和交叉验证集误差作为训练集实例数量(𝑚)的函数绘制的图表。
如果用二次曲线从一个数据开始慢慢拟合更多的数据,训练集误差将会慢慢变大,这是因为当1个或者两个数据的时候可以完美拟合,但是当四个或者五个数据的时候就会出现一些偏差,导致训练集误差不如数据较少的时候。
为什么交叉验证误差会比训练集误差更大一些呢?因为在训练模型的时候,我们希望能在训练集上表现得更好,即使在m(训练数据集数量)较小的时候也是如此,也就是当训练较少数据的时候,训练的模型将能够非常完美地适应较少的训练数据,但是训练出来的模型却不能很好地适应交叉验证集数据或测试集数据。所以会出现以下这种曲线。
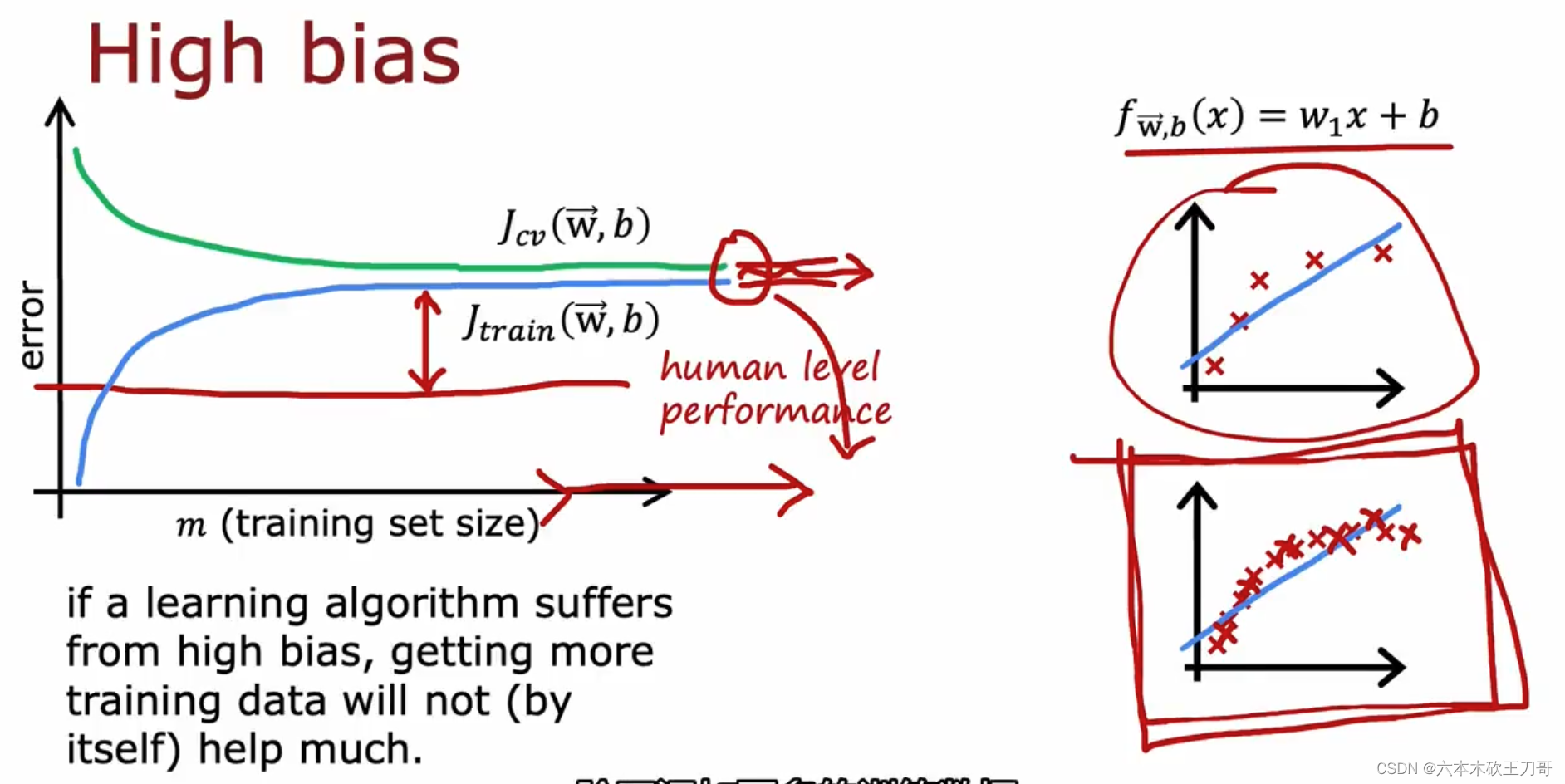
如何利用学习曲线识别高偏差/欠拟合:作为例子,我们尝试用一条直线来适应下面的数据,可以看出,无论训练集有多么大误差都不会有太大改观。也就是说在高偏差/欠拟合的情况下,增加数据到训练集不一定能有帮助。
如何利用学习曲线识别高方差/过拟合:假设我们使用一个非常高次的多项式模型,并且正则化非常小,可以看出,当交叉验证集误差远大于训练集误差时(因为过拟合),并且人类自身的表现误差甚至高于这个模型(因为过拟合,训练数据表现的太好),往训练集增加更多数据可以提高模型的效果。也就是说在高方差/过拟合的情况下,增加更多数据到训练集可能可以提高算法效果。
9.2.5 解决高偏差或者高方差的各种情况
我们已经介绍了怎样评价一个学习算法,我们讨论了模型选择问题,偏差和方差的问题。 那么这些诊断法则怎样帮助我们判断,哪些方法可能有助于改进学习算法的效果,而哪些可能是徒劳的呢?
让我们再次回到最开始的例子,在那里寻找答案,这就是我们之前的例子。回顾 提出的六种可选的下一步,让我们来看一看我们在什么情况下应该怎样选择:
1. 获得更多的训练实例——解决高方差
2. 尝试减少特征的数量——解决高方差
3. 尝试获得更多的特征——解决高偏差
4. 尝试增加多项式特征——解决高偏差
5. 尝试减少正则化程度 λ——解决高偏差
6. 尝试增加正则化程度 λ——解决高方差
9.2.6 神经网络的方差和偏差
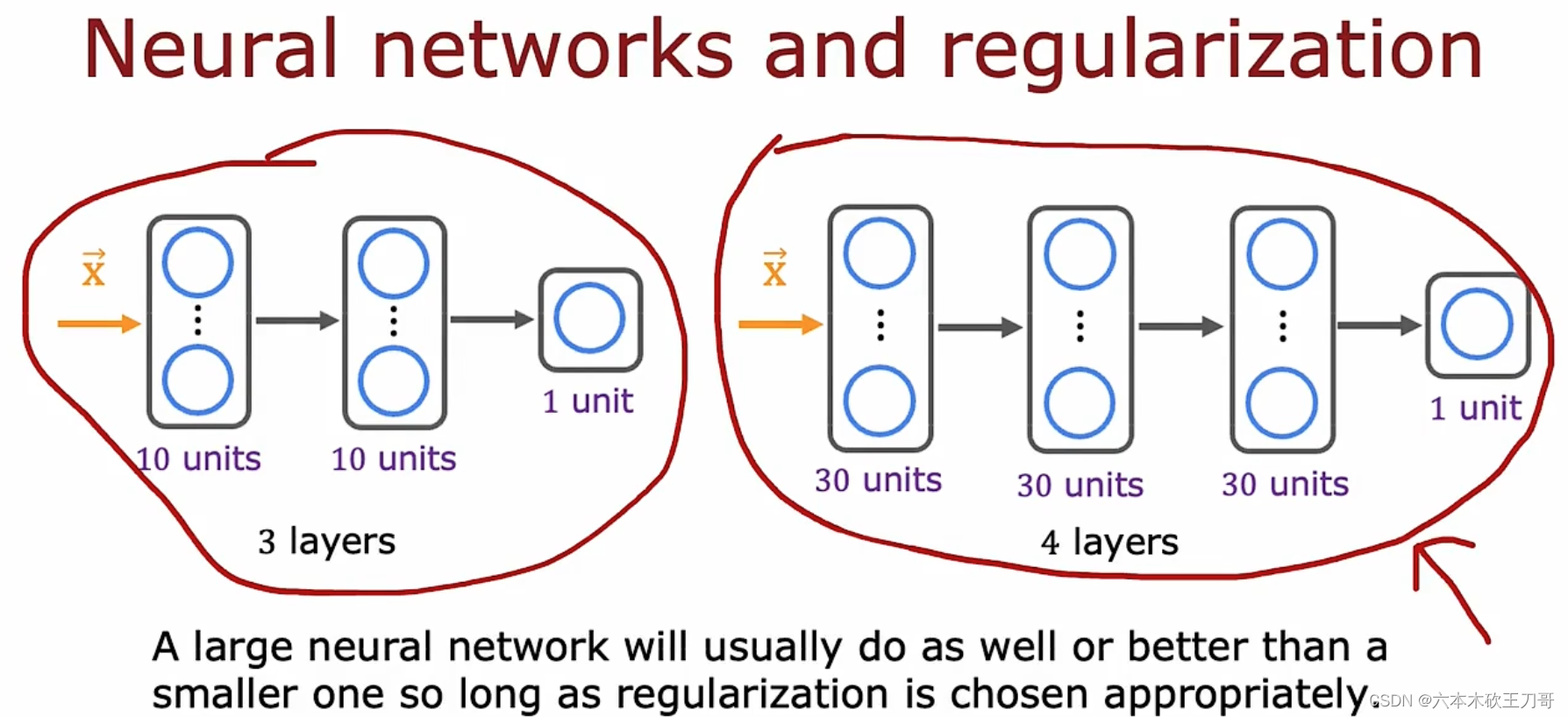
使用较小的神经网络,类似于参数较少的情况,容易导致高偏差和欠拟合,但计算代价较小;使用较大的神经网络,类似于参数较多的情况,容易导致高方差和过拟合,虽然计算代价比较大,但是可以通过正则化手段来调整而更加适应数据。
如何根据偏差和方差来训练一个神经网络?下图演示了这个步骤。
如果神经网络较大,担心产生高方差问题该怎么办?
通常选择较大的神经网络并采用正则化处理会比采用较小的神经网络效果要好,所以通常情况下使用较大神经网络会导致训练时间过长,但这个并没有太多的损害。
对于神经网络中的隐藏层的层数的选择,通常从一层开始逐渐增加层数,为了更好地作选择,可以把数据分为训练集、交叉验证集和测试集,针对不同隐藏层层数的神经网络训练神经网络, 然后选择交叉验证集代价最小的神经网络。
下面的代码展示了如果在TensorFlow中进行正则化的训练,在初始化每个隐藏层的时候加入正则化参数即可。
以上就是我们介绍的偏差和方差问题,以及诊断该问题的学习曲线方法。在改进学习算法的表现时,你可以充分运用以上这些内容来判断哪些途径可能是有帮助的。而哪些方法可能是无意义的。如果你理解了以上几节视频中介绍的内容,并且懂得如何运用。那么你已经可以使用机器学习方法有效的解决实际问题了。你也能像硅谷的大部分机器学习从业者一样,他们每天的工作就是使用这些学习算法来解决众多实际问题。我希望这几节中提 到的一些技巧,关于方差、偏差,以及学习曲线为代表的诊断法能够真正帮助你更有效率地应用机器学习,让它们高效地工作。