文章目录
一、理论基础
1、哈里斯鹰优化算法
请参考这里。
2、改进的哈里斯鹰优化算法
(1)反向学习策略
作为改善种群多样性的有效方法,反向学习(Opposition-based learning, OBL)策略被广泛应用于改进智能算法。OBL的主要思想是同时考虑候选解和反向解的相对优点,选择更好的解进入下一代种群,从而更好地提高算法的收敛速度和求解精度。
定义:设
X
=
(
x
1
,
x
2
,
⋯
,
x
D
)
X=(x_1,x_2,\cdots,x_D)
X=(x1,x2,⋯,xD)是
D
D
D维空间中的一个点,其中
x
j
∈
[
L
b
j
,
U
b
j
]
,
j
=
1
,
2
,
⋯
,
D
x_j\in[Lb_j,Ub_j],j=1,2,\cdots,D
xj∈[Lbj,Ubj],j=1,2,⋯,D,将
X
X
X的反向点设为
X
˘
=
(
x
˘
1
,
x
˘
2
,
⋯
,
x
˘
D
)
\breve X=(\breve x_1,\breve x_2,\cdots,\breve x_D)
X˘=(x˘1,x˘2,⋯,x˘D),准反向点设为
X
~
=
(
x
~
1
,
x
~
2
,
⋯
,
x
~
D
)
\tilde X=(\tilde x_1,\tilde x_2,\cdots,\tilde x_D)
X~=(x~1,x~2,⋯,x~D),准反射点设为
X
ˉ
=
(
x
ˉ
1
,
x
ˉ
2
,
⋯
,
x
ˉ
D
)
\bar X=(\bar x_1,\bar x_2,\cdots,\bar x_D)
Xˉ=(xˉ1,xˉ2,⋯,xˉD),其中:
x
˘
j
=
L
b
j
+
U
b
j
−
x
j
(1)
\breve x_j=Lb_j+Ub_j-x_j\tag{1}
x˘j=Lbj+Ubj−xj(1)
x
~
j
=
r
a
n
d
[
(
L
b
j
+
U
b
j
2
)
,
(
L
b
j
+
U
b
j
−
x
j
)
]
(2)
\tilde x_j=rand\left[\left(\frac{Lb_j+Ub_j}{2}\right),(Lb_j+Ub_j-x_j)\right]\tag{2}
x~j=rand[(2Lbj+Ubj),(Lbj+Ubj−xj)](2)
x
ˉ
j
=
r
a
n
d
[
(
L
b
j
+
U
b
j
2
)
,
x
j
]
(3)
\bar x_j=rand\left[\left(\frac{Lb_j+Ub_j}{2}\right),x_j\right]\tag{3}
xˉj=rand[(2Lbj+Ubj),xj](3)根据HHO算法开发阶段的四种更新方法,当
r
≥
0.5
,
∣
E
∣
≥
0.5
r\geq0.5,|E|\geq0.5
r≥0.5,∣E∣≥0.5时,鹰群个体需要在大范围内搜索以捕捉猎物。此时,为了扩大搜索范围,在使用原始公式进行位置更新后,对第
i
i
i个个体
X
i
o
l
d
(
t
+
1
)
X_i^{old}(t+1)
Xiold(t+1)采用准反向学习策略。因此,它在远离候选解的邻域中生成一个准反向解
X
~
i
(
t
+
1
)
\tilde X_i(t+1)
X~i(t+1)。贪婪选择策略用于从准反向解和原始个体中选择父代个体以进入下一代,如式(4)所示。
X
i
(
t
+
1
)
=
{
X
i
o
l
d
(
t
+
1
)
,
if
F
(
X
i
o
l
d
(
t
+
1
)
)
<
F
(
X
~
i
(
t
+
1
)
)
X
~
i
(
t
+
1
)
,
otherwise
(4)
X_i(t+1)=\begin{dcases}X_i^{old}(t+1),\quad\,\text{if}\,\,F(X_i^{old}(t+1))<F(\tilde X_i(t+1))\\[2ex]\tilde X_i(t+1),\quad\quad\text{otherwise}\end{dcases}\tag{4}
Xi(t+1)=⎩
⎨
⎧Xiold(t+1),ifF(Xiold(t+1))<F(X~i(t+1))X~i(t+1),otherwise(4)当
r
≥
0.5
,
∣
E
∣
<
0.5
r\geq0.5,|E|<0.5
r≥0.5,∣E∣<0.5,鹰种群可以在小范围内捕捉猎物。此时,对第
i
i
i个个体
X
i
o
l
d
(
t
+
1
)
X_i^{old}(t+1)
Xiold(t+1)采用准反射学习策略,以进一步增强其开发能力。在靠近候选解的邻域中生成准反射解。通过贪婪选择,更好的个体被保留下来,用于下一次迭代更新,如式(5)所示。
X
i
(
t
+
1
)
=
{
X
i
o
l
d
(
t
+
1
)
,
if
F
(
X
i
o
l
d
(
t
+
1
)
)
<
F
(
X
ˉ
i
(
t
+
1
)
)
X
ˉ
i
(
t
+
1
)
,
otherwise
(5)
X_i(t+1)=\begin{dcases}X_i^{old}(t+1),\quad\,\text{if}\,\,F(X_i^{old}(t+1))<F(\bar X_i(t+1))\\[2ex]\bar X_i(t+1),\quad\quad\text{otherwise}\end{dcases}\tag{5}
Xi(t+1)=⎩
⎨
⎧Xiold(t+1),ifF(Xiold(t+1))<F(Xˉi(t+1))Xˉi(t+1),otherwise(5)随机使用上述准反向和准反射策略,并根据不同个体的行为选择适当的搜索策略,可以加快算法在开发后期的优化效率,提高算法的全局收敛能力。然而,值得注意的是,贪婪选择提高了算法的收敛速度,同时增加了函数的估计次数和算法的运行时间。
(2)非线性收敛因子调整策略
本文提出对数非线性能量衰减策略,其对应的能量方程为:
a
(
t
)
=
1
−
ln
(
1
+
t
(
e
−
1
)
T
)
(6)
a(t)=1-\ln\left(1+\frac{t(e-1)}{T}\right)\tag{6}
a(t)=1−ln(1+Tt(e−1))(6)
E
=
2
E
0
a
(
t
)
(7)
E=2E_0a(t)\tag{7}
E=2E0a(t)(7)其中,
e
e
e是自然常数,
t
t
t是当前迭代次数,
T
T
T是最大迭代次数,
E
0
E_0
E0是初始逃逸能量。
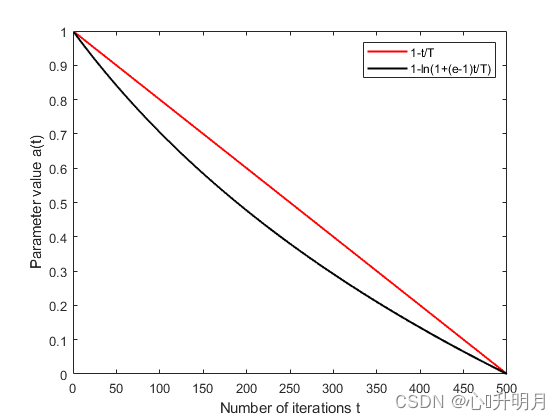
随着迭代次数
t
t
t的增加,收敛因子
a
(
t
)
a(t)
a(t)从1非线性减小到0,
(
1
−
t
/
T
)
(1-t/T)
(1−t/T)和
a
(
t
)
a(t)
a(t)的变化曲线如图1所示。图1表明,与
(
1
−
t
/
T
)
(1-t/T)
(1−t/T)的线性变化相比,
a
(
t
)
a(t)
a(t)的非线性变化使其在迭代的早期下降较快,在后期下降较慢。由于HHO算法的种群多样性在迭代的早期更好,因此有必要在迭代的后期确保强大的局部开发能力。因此,本文给出的调整参数可以更好地满足早期探索和后期开发之间更稳定的过渡,使算法能够确保探索和开发之间的平衡,进一步提高HHO算法的收敛速度和求解精度。
(3)随机无迹sigma点变异策略
为了提高HHO算法的收敛速度和计算精度,对当前最优解进行变异是一种简单有效的方法。操作的实质是在当前最优解的可见范围内进行精细开发,以实现当前开发范围内的进一步优化。无迹sigma点变换使用关于随机变量
x
ˉ
\bar x
xˉ的均值
x
x
x和方差
P
x
P_x
Px的信息来生成
2
D
+
1
2D+1
2D+1个点,用于估计随机变量
x
x
x给定函数的均值和方差。无迹sigma点的生成原理如式(8)所示:
{
ξ
0
′
=
x
ˉ
ξ
0
′
=
x
ˉ
+
(
(
D
+
κ
)
P
x
)
i
i
=
1
,
2
,
⋯
,
D
ξ
i
+
D
′
=
x
ˉ
−
(
(
D
+
κ
)
P
x
)
i
i
=
1
,
2
,
⋯
,
D
(8)
\begin{dcases}\xi_0'=\bar x\\[2ex]\xi_0'=\bar x+\left(\sqrt{(D+\kappa)P_x}\right)_i\quad\quad i=1,2,\cdots,D\\[2ex]\xi_{i+D}'=\bar x-\left(\sqrt{(D+\kappa)P_x}\right)_i\quad i=1,2,\cdots,D\end{dcases}\tag{8}
⎩
⎨
⎧ξ0′=xˉξ0′=xˉ+((D+κ)Px)ii=1,2,⋯,Dξi+D′=xˉ−((D+κ)Px)ii=1,2,⋯,D(8)其中,
κ
=
α
2
(
D
+
λ
)
−
D
\kappa=\alpha^2(D+\lambda)-D
κ=α2(D+λ)−D;
λ
=
3
−
D
\lambda=3-D
λ=3−D;
α
\alpha
α是一个非常小的正数,本文取值为
1
×
1
0
−
2
1\times 10^{-2}
1×10−2;
D
D
D是问题的维数;
x
ˉ
\bar x
xˉ是
x
x
x的平均值,
P
x
P_x
Px是
x
x
x的协方差矩阵,以及
(
(
D
+
κ
)
P
x
)
i
\left(\sqrt{(D+\kappa)P_x}\right)_i
((D+κ)Px)i是
(
D
+
κ
)
P
x
(D+\kappa)P_x
(D+κ)Px的平方根矩阵的第
i
i
i列。
本文以当前最优个体的位置作为均值,以当前种群的方差作为域范围。UT生成的点位于超椭球体上,每个方向上的两个点与中心的距离相同。当前最优解的随机UT使同一方向上的点更加灵活,快速定位当前最优解以提高算法的计算精度。对当前种群的最优个体
X
∗
o
l
d
(
t
)
X_*^{old}(t)
X∗old(t)随机变异产生
2
D
+
1
2D+1
2D+1突变点,如式(9)所示。
{
X
0
′
=
X
∗
o
l
d
(
t
)
X
i
′
=
X
∗
o
l
d
(
t
)
+
r
(
(
D
+
κ
)
P
x
)
i
i
=
1
,
2
,
⋯
,
D
X
i
+
D
′
=
X
∗
o
l
d
(
t
)
−
r
(
(
D
+
κ
)
P
x
)
i
i
=
1
,
2
,
⋯
,
D
(9)
\begin{dcases}X_0'=X_*^{old}(t)\\[2ex]X_i'=X_*^{old}(t)+r\left(\sqrt{(D+\kappa)P_x}\right)_i\quad\quad i=1,2,\cdots,D\\[2ex]X_{i+D}'=X_*^{old}(t)-r\left(\sqrt{(D+\kappa)P_x}\right)_i\quad i=1,2,\cdots,D\end{dcases}\tag{9}
⎩
⎨
⎧X0′=X∗old(t)Xi′=X∗old(t)+r((D+κ)Px)ii=1,2,⋯,DXi+D′=X∗old(t)−r((D+κ)Px)ii=1,2,⋯,D(9)
r
=
cos
(
π
2
⋅
t
T
)
(10)
r=\cos\left(\frac\pi2\cdot\frac tT\right)\tag{10}
r=cos(2π⋅Tt)(10)其中,
r
r
r是单调递减比例因子,这确保了随着迭代次数的增加,可以在小范围的最优解中精准利用该算法;
P
x
P_x
Px是当前种群的方差,决定了最优解的可视范围。计算
2
D
+
1
2D+1
2D+1变异个体的适应度值,并通过贪婪搜索更新当前最优个体,即:
X
∗
(
t
+
1
)
=
arg
min
0
≤
i
≤
2
D
{
F
(
X
i
′
)
}
(11)
X_*(t+1)=\arg\min_{0\leq i\leq 2D}\left\{F(X_i')\right\}\tag{11}
X∗(t+1)=arg0≤i≤2Dmin{F(Xi′)}(11)
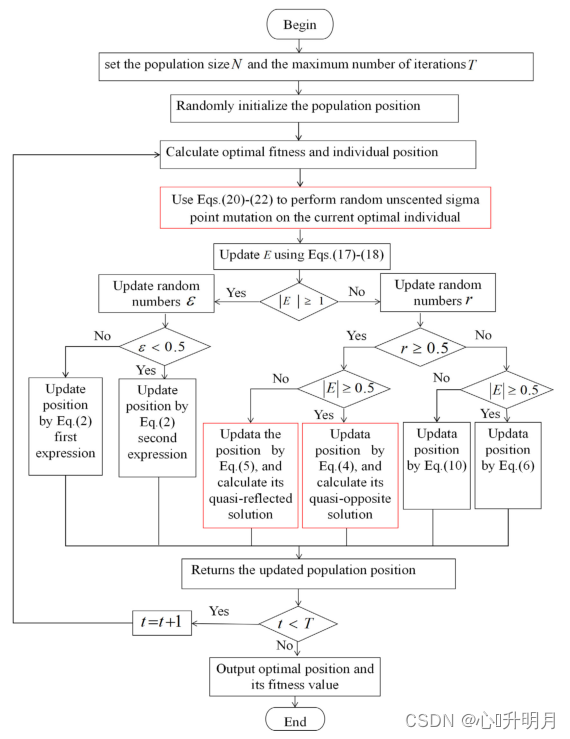
(4)IHHO算法流程图
IHHO算法流程图如图2所示。
二、仿真实验与结果分析
将IHHO与GWO、TSA、WOA和HHO进行对比,以常用23个测试函数中的F5、F6(单峰函数/30维)、F9、F10(多峰函数/30维)、F16、F17(固定维度多峰函数/2维、2维)为例,实验设置种群规模为30,最大迭代次数为500,每种算法独立运算30次,结果显示如下:
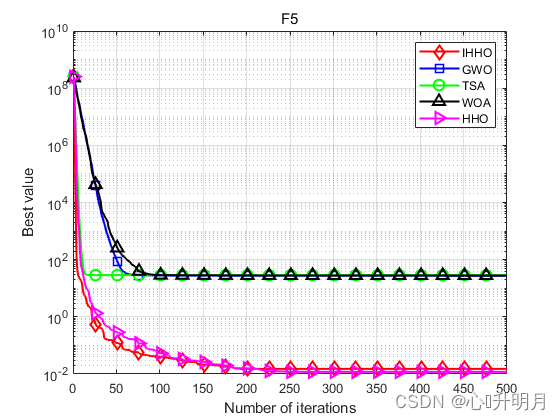
函数:F5
IHHO:最差值: 0.13865, 最优值: 7.0741e-07, 平均值: 0.015084, 标准差: 0.028063, 秩和检验: 1
GWO:最差值: 28.7782, 最优值: 25.7691, 平均值: 27.1844, 标准差: 0.89806, 秩和检验: 3.0199e-11
TSA:最差值: 28.9205, 最优值: 28.0782, 平均值: 28.656, 标准差: 0.29311, 秩和检验: 3.0199e-11
WOA:最差值: 28.7296, 最优值: 26.995, 平均值: 27.9626, 标准差: 0.5061, 秩和检验: 3.0199e-11
HHO:最差值: 0.06623, 最优值: 6.9462e-06, 平均值: 0.011919, 标准差: 0.015624, 秩和检验: 0.81875
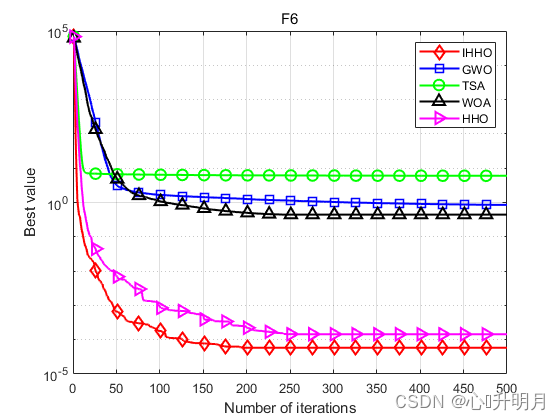
函数:F6
IHHO:最差值: 0.00029011, 最优值: 4.1743e-07, 平均值: 5.8064e-05, 标准差: 7.8979e-05, 秩和检验: 1
GWO:最差值: 2.0136, 最优值: 0.47823, 平均值: 0.85263, 标准差: 0.40313, 秩和检验: 3.0199e-11
TSA:最差值: 7.0002, 最优值: 3.4834, 平均值: 5.9968, 标准差: 0.89309, 秩和检验: 3.0199e-11
WOA:最差值: 0.98535, 最优值: 0.12858, 平均值: 0.44196, 标准差: 0.19807, 秩和检验: 3.0199e-11
HHO:最差值: 0.00073833, 最优值: 1.5022e-09, 平均值: 0.00014427, 标准差: 0.00017396, 秩和检验: 0.033874
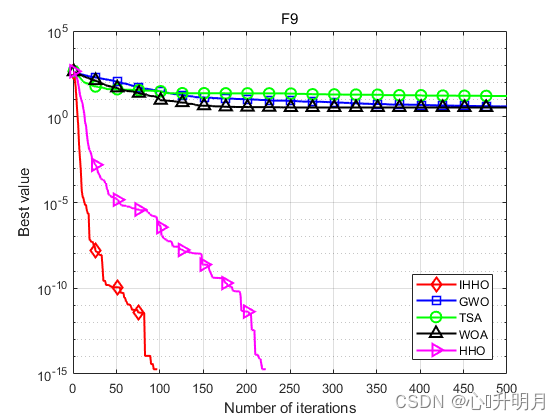
函数:F9
IHHO:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
GWO:最差值: 16.578, 最优值: 5.6843e-14, 平均值: 4.0017, 标准差: 5.4482, 秩和检验: 1.2019e-12
TSA:最差值: 162.0057, 最优值: 0, 平均值: 16.2838, 标准差: 44.1385, 秩和检验: 3.4526e-07
WOA:最差值: 104.4303, 最优值: 0, 平均值: 3.481, 标准差: 19.0663, 秩和检验: 0.1608
HHO:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
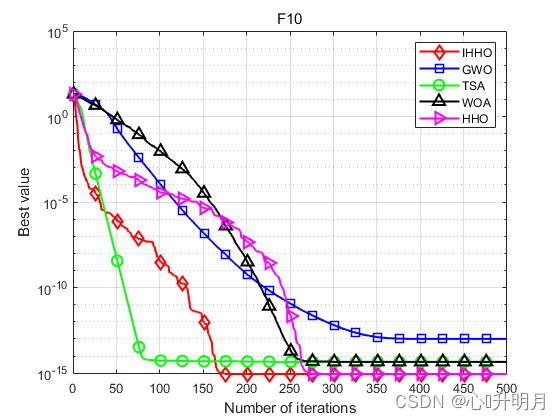
函数:F10
IHHO:最差值: 8.8818e-16, 最优值: 8.8818e-16, 平均值: 8.8818e-16, 标准差: 0, 秩和检验: NaN
GWO:最差值: 1.4655e-13, 最优值: 6.1284e-14, 平均值: 9.989e-14, 标准差: 1.983e-14, 秩和检验: 1.1738e-12
TSA:最差值: 4.4409e-15, 最优值: 4.4409e-15, 平均值: 4.4409e-15, 标准差: 0, 秩和检验: 1.6853e-14
WOA:最差值: 7.9936e-15, 最优值: 8.8818e-16, 平均值: 4.5593e-15, 标准差: 2.5523e-15, 秩和检验: 3.858e-09
HHO:最差值: 8.8818e-16, 最优值: 8.8818e-16, 平均值: 8.8818e-16, 标准差: 0, 秩和检验: NaN
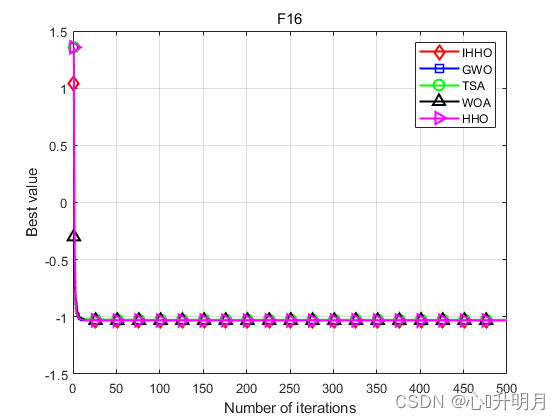
函数:F16
IHHO:最差值: -1.0316, 最优值: -1.0316, 平均值: -1.0316, 标准差: 8.1181e-11, 秩和检验: 1
GWO:最差值: -1.0316, 最优值: -1.0316, 平均值: -1.0316, 标准差: 2.8673e-08, 秩和检验: 3.018e-11
TSA:最差值: -0.99999, 最优值: -1.0316, 平均值: -1.0253, 标准差: 0.012862, 秩和检验: 3.018e-11
WOA:最差值: -1.0316, 最优值: -1.0316, 平均值: -1.0316, 标准差: 1.0089e-09, 秩和检验: 8.2895e-06
HHO:最差值: -1.0316, 最优值: -1.0316, 平均值: -1.0316, 标准差: 2.0929e-09, 秩和检验: 0.2062
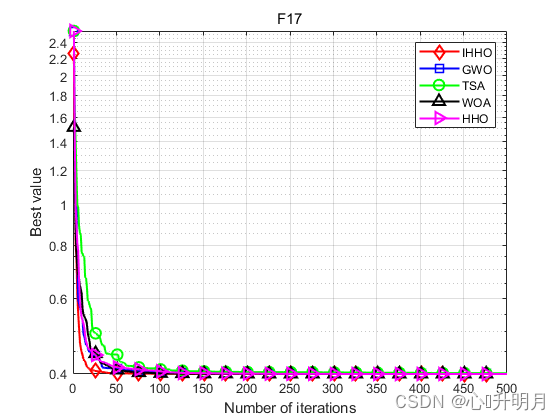
函数:F17
IHHO:最差值: 0.39789, 最优值: 0.39789, 平均值: 0.39789, 标准差: 5.6785e-07, 秩和检验: 1
GWO:最差值: 0.3979, 最优值: 0.39789, 平均值: 0.39789, 标准差: 1.8596e-06, 秩和检验: 5.3124e-09
TSA:最差值: 0.40322, 最优值: 0.39789, 平均值: 0.39939, 标准差: 0.0015405, 秩和检验: 3.5611e-11
WOA:最差值: 0.39791, 最优值: 0.39789, 平均值: 0.39789, 标准差: 5.7596e-06, 秩和检验: 3.0387e-06
HHO:最差值: 0.3979, 最优值: 0.39789, 平均值: 0.39789, 标准差: 1.5509e-06, 秩和检验: 0.0022272
实验结果表明:IHHO算法具有更好的全局探索和局部开发能力,在求解精度和收敛速度方面优于其他比较算法。
三、参考文献
[1] Wenyan Guo, Peng Xu, Fang Dai, et al. Improved Harris hawks optimization algorithm based on random unscented sigma point mutation strategy[J]. Applied Soft Computing, 2021, 113: 108012.