◆
输入输出描述法
描述一个系统,可以不管系统内部的结构如何,将系统看成一个黑盒子,只描述或者研究系统输出和输入之间的关系
模拟系统:微分方程描述
离散时间系统:差分方程描述
线性时不变系统:常用线性常系数差分方程
◆ 一个
N阶线性常系数差分方程用下式表示:
 (2.3.1)
(2.3.1)
或者
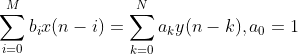 (2.3.2)
(2.3.2)
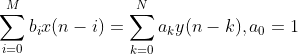 (2.3.2)
(2.3.2)
式中
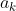 和
和
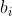 均为常数
均为常数
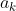 和
和
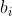 均为常数
均为常数
➢
线性
:式中
y(
n-
k)和
x(
n-
i)项只有一次幂,也没有相
 (2.3.1)
(2.3.1)
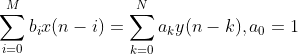 (2.3.2)
(2.3.2)


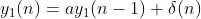 和例2.3.1(2)相同,输出
通式为:
和例2.3.1(2)相同,输出
通式为:
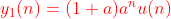
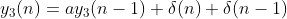
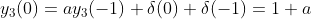
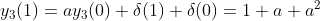
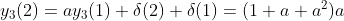
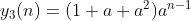
互交叉项,故称为线性常系数差分方程
➢
阶数
:由方程
y(
n-
k)项中
k的取值最大与最小之差确定。在(2.3.2)式中,
y(
n-
k)项
k最大的取值为
N,
k的 最小取值为零,因此称为
N 阶差分方程。
◆ 已知系统的输入序列,通过求解差分方程可求输出序列
◆ 求解差分方程的基本方法有:
➢ 变换域方法:
Z变换
➢ 时域解法
经典解法:闭合形式的解(齐次解和特解),应用少。
递推解法:数值解(本节详细讨论)
已知:输入序列和
N个初始条件
求解:
n时刻的输出,并递推求出
n+1时刻的输出
◆ 差分方程本身就是一个适合递推法求解的方程
 (2.3.1)
(2.3.1)
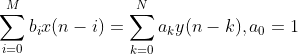 (2.3.2)
(2.3.2)
◆
重点:讨论初始条件对线性、时不变性、因果性、稳定性的影响
例 2.3.1 设系统用差分方程
y(
n)=
ay(
n-1)+
x(
n)描述,输入序列
x(
n)=
δ(
n),求输出序列
y(
n)
解:该系统差分方程是一阶差分方程,需要一个初始条件
(1)
设初始条件
y(-1)=0
y
(
n
)=
a
y(
n
-1)+
x
(
n
)
n=0时,
y(0)=
ay(0-1)+
x(0)=
ay(-1)+
δ(0)=1
n=1时,
y(1)=
ay(1-1)+
x(1)=
ay(0)+
δ(1)=a
n=2时,
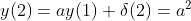
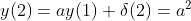
…
n=
n时,



(2)
设初始条件
y
(-1)=1
n=0时,
y(0)=
ay(-1)+
δ(0)=1+
a
n=1时,
y(1)=
ay(0)+
δ(1)=(1+
a)
a
n=2时,
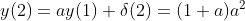
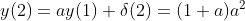
…
n=
n时,
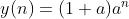
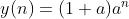

◆
分 析
对于同一个差分方程和同一个输入信号,因为初始条件不同,得到的输出信号是不相同的
对于
实际系统,用递推解法求解,总是由初始条件向
n>0的方向递推,是一个因果解
但对于
差分方程,其本身也可以向
n<0的方向递推,得到的是非因果解
结论1:差分方程本身并不能确定该系统是因果还是非因果系统,还需要用初始条件进行限制(因果性:在
n<0时,没有加入信号, 输出只能等于零)
结论2:线性常系数差分方程描述的系统并不一定是线性时不变系统,这和系统的初始状态有关
例2.3.2 设系统用一阶差分方程
y(
n)=
ay(
n-1)+
x(
n)描述,初始条件
y(-1)=1,试分析该系统是否是线性时不变系统
下面通过设输入信号
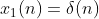 ,
,
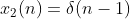 和
和
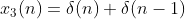 来检验系统是否是线性时不变
来检验系统是否是线性时不变
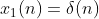 ,
,
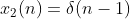 和
和
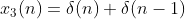 来检验系统是否是线性时不变
来检验系统是否是线性时不变
(1)
x
1
(
n
)=
δ
(
n
),
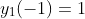
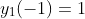
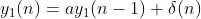 和例2.3.1(2)相同,输出
通式为:
和例2.3.1(2)相同,输出
通式为:
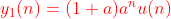
(3)
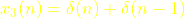 ;
;
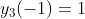
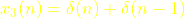 ;
;
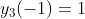
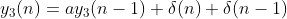
n=0时,
n=1时,
n=2时,…
n=
n时,
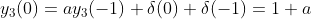
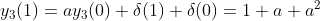
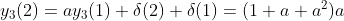
…
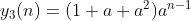
◆采用线性常系数差分方程描述系统时,如果没有附加的约束条件,则它不能唯一地确定一个系统的输
入和输出关系,也不能保证系统一定是线性时不变系统
◆约定:凡用线性常系数差分方程所描述的系统都是指线性时不变系统
(觉得这篇笔记对你有点用的话,麻烦你为本笔记点赞,评论,分享或收藏,因为这将是我输出更多笔记的动力,感谢!)
👇 👇 👇 👇