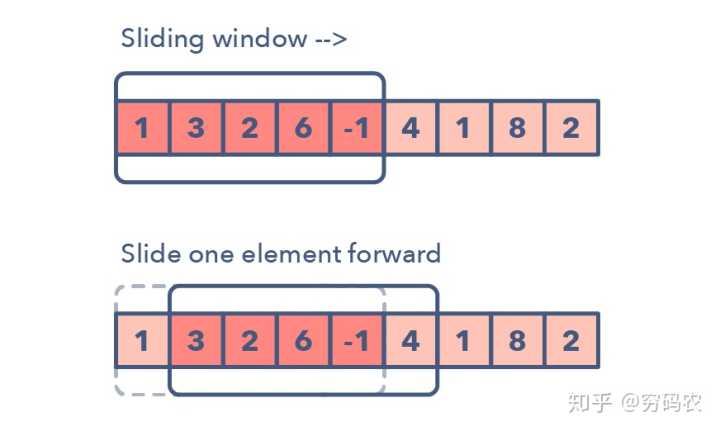
Sliding window,滑动窗口类型
介绍部分来自:https://www.zhihu.com/question/36738189/answer/908664455
滑动窗口类型的题目经常是用来执行数组或是链表上某个区间(窗口)上的操作。比如找最长的全为1的子数组长度。滑动窗口一般从第一个元素开始,一直往右边一个一个元素挪动。当然了,根据题目要求,我们可能有固定窗口大小的情况,也有窗口的大小变化的情况。
下面是一些我们用来判断我们可能需要上滑动窗口策略的方法:
- 这个问题的输入是一些线性结构:比如链表呀,数组啊,字符串啊之类的
- 让你去求最长/最短子字符串或是某些特定的长度要求
以下来自:https://labuladong.gitbook.io/algo/di-ling-zhang-bi-du-xi-lie/hua-dong-chuang-kou-ji-qiao-jin-jie
滑动窗口算法的思路是这样:
1、我们在字符串 S 中使用双指针中的左右指针技巧,初始化 left = right = 0,把索引左闭右开区间 [left, right) 称为一个「窗口」。
2、我们先不断地增加 right 指针扩大窗口 [left, right),直到窗口中的字符串符合要求(包含了 T 中的所有字符)。
3、此时,我们停止增加 right,转而不断增加 left 指针缩小窗口 [left, right),直到窗口中的字符串不再符合要求(不包含 T 中的所有字符了)。同时,每次增加 left,我们都要更新一轮结果。
4、重复第 2 和第 3 步,直到 right 到达字符串 S 的尽头。
这个思路其实也不难,**第 2 步相当于在寻找一个「可行解」,然后第 3 步在优化这个「可行解」,最终找到最优解,**也就是最短的覆盖子串。左右指针轮流前进,窗口大小增增减减,窗口不断向右滑动,这就是「滑动窗口」这个名字的来历。
该算法的大致逻辑如下:
int left = 0, right = 0;
while (right < s.size()) {`
// 增大窗口
window.add(s[right]);
right++;
while (window needs shrink) {
// 缩小窗口
window.remove(s[left]);
left++;
}
}
算法框架:
/* 滑动窗口算法框架 */
void slidingWindow(string s, string t) {
unordered_map<char, int> need, window;
for (char c : t) need[c]++;
int left = 0, right = 0;
int valid = 0;
while (right < s.size()) {
// c 是将移入窗口的字符
char c = s[right];
// 右移窗口
right++;
// 进行窗口内数据的一系列更新
...
/*** debug 输出的位置 ***/
printf("window: [%d, %d)\n", left, right);
/********************/
// 判断左侧窗口是否要收缩
while (window needs shrink) {
// d 是将移出窗口的字符
char d = s[left];
// 左移窗口
left++;
// 进行窗口内数据的一系列更新
...
}
}
}
经典题目:
1、Maximum Sum Subarray of Size K (easy)
描述
给一个数组nums和目标值k,找到数组中最长的子数组,使其中的元素和为k。如果没有,则返回0。
数组之和保证在32位有符号整型数的范围内
样例
样例1
输入: nums = [1, -1, 5, -2, 3], k = 3
输出: 4
解释:
子数组[1, -1, 5, -2]的和为3,且长度最大
样例2
输入: nums = [-2, -1, 2, 1], k = 1
输出: 2
解释:
子数组[-1, 2]的和为1,且长度最大
前缀和技巧
https://zhuanlan.zhihu.com/p/107778275
一、什么是前缀和
前缀和的思路是这样的,对于一个给定的数组 nums,我们额外开辟一个前缀和数组进行预处理:
int n = nums.length;
// 前缀和数组
int[] preSum = new int[n + 1];
preSum[0] = 0;
for (int i = 0; i < n; i++)
preSum[i + 1] = preSum[i] + nums[i];
这个前缀和数组 preSum 的含义也很好理解,preSum[i] 就是 nums[0..i-1] 的和。那么如果我们想求 nums[i..j] 的和,只需要一步操作 preSum[j+1]-preSum[i] 即可,而不需要重新去遍历数组了。
/**
* 前缀和算法
* put 与 putIfAbsent区别:
*
* put在放入数据时,如果放入数据的key已经存在与Map中,最后放入的数据会覆盖之前存在的数据,而putIfAbsent在放入数据时,如果存在重复的key,那么
* putIfAbsent不会放入值。
* putIfAbsent 如果传入key对应的value已经存在,就返回存在的value,不进行替换。如果不存在,就添加key和value,返回null
*
* @param nums nums = [1, -1, 5, -2, 3]
* @param k k = 3
* @return 输出: 4
*/
public static int maxSubArrayLen1(int[] nums, int k) {
// Write your code here
Map<Integer, Integer> map = new HashMap<>(); // sum -> id 前缀和数组为 hashmap 中的 key, id 为下标
map.put(0, -1); // 这里需要第一个元素为 0
int maxLen = 0;
for (int i = 0, sum = 0; i < nums.length; i++) {
sum += nums[i];
if (map.containsKey(sum - k)) { // sum[i] - k = sum[j] 说明前缀和i - 前缀和j = k
maxLen = Math.max(maxLen, i - map.get(sum - k)); // i - j = 区间大小
} else {
map.putIfAbsent(sum, i);
}
}
return maxLen;
}
2、Smallest Subarray with a given sum (easy)
3、Longest Substring with K Distinct Characters (medium)
描述
给定字符串S,找到最多有k个不同字符的最长子串T。
样例
样例 1:
输入: S = "eceba" 并且 k = 3
输出: 4
解释: T = "eceb"
样例 2:
输入: S = "WORLD" 并且 k = 4
输出: 4
解释: T = "WORL" 或 "ORLD"
算法:
/**
* @param s: A string
* @param k: An integer
* @return: An integer
*/
public static int lengthOfLongestSubstringKDistinct(String s, int k) {
// write your code here
if (s.length() == 0 || k == 0)
return 0;
int res = 0; // 结果
char[] ch = s.toCharArray(); // 字符数组
// 窗口 [left, right)
int left = 0; // 左指针
int right = 0; // 右指针
Map<Character, Integer> windowMap = new HashMap<>(); // 窗口 字符->出现次数
while(right < s.length()){
char c = ch[right]; // 将移入窗口的字符
right++; // 右移
// 进行窗口内数据的一些列更新
if (windowMap.containsKey(c)){
windowMap.put(c, windowMap.get(c) + 1); // 更新出现次数
}else{
windowMap.put(c, 1);
}
// 判断是否要收缩窗口
while (windowMap.size() > k){
char lc = ch[left]; // 要移除的字符
left++; // 左窗口右移
// 进行窗口内数据的一些列更新
int count = windowMap.get(lc);
if (count > 1) {
windowMap.put(lc, windowMap.get(lc) - 1);
}else {
windowMap.remove(lc);
}
}
// 更新答案
res = Math.max(res, right - left);
}
return res;
}
4、Fruits into Baskets (medium)
904. 水果成篮
类似:928. 最多有两个不同字符的最长子串
描述
在一排树中,第 i 棵树产生 tree[i] 型的水果。
你可以从你选择的任何树开始,然后重复执行以下步骤:
把这棵树上的水果放进你的篮子里。如果你做不到,就停下来。
移动到当前树右侧的下一棵树。如果右边没有树,就停下来。
请注意,在选择一颗树后,你没有任何选择:你必须执行步骤 1,然后执行步骤 2,然后返回步骤 1,然后执行步骤 2,依此类推,直至停止。
你有两个篮子,每个篮子可以携带任何数量的水果,但你希望每个篮子只携带一种类型的水果。
用这个程序你能收集的水果树的最大总量是多少?
示例 :
示例 1 :
输入:[1,2,1]
输出:3
解释:我们可以收集 [1,2,1]。
示例 2:
输入:[0,1,2,2]
输出:3
解释:我们可以收集 [1,2,2]
如果我们从第一棵树开始,我们将只能收集到 [0, 1]。
示例 3:
输入:[1,2,3,2,2]
输出:4
解释:我们可以收集 [2,3,2,2]
如果我们从第一棵树开始,我们将只能收集到 [1, 2]。
示例 4:
输入:[3,3,3,1,2,1,1,2,3,3,4]
输出:5
解释:我们可以收集 [1,2,1,1,2]
如果我们从第一棵树或第八棵树开始,我们将只能收集到 4 棵水果树。
public static int totalFruit(int[] tree) {
if (tree.length == 0)
return 0;
int res = 0; // 结果
int left = 0; // 左指针
int right = 0; // 右指针
Map<Integer, Integer> windowMap = new HashMap<>(); // 窗口
while (right < tree.length){
int ri = tree[right]; // 进入右窗口的值
right++; // 右移
// 进行窗口内数据的一系列更新
windowMap.put(ri, windowMap.getOrDefault(ri, 0) + 1);
// 判断是否需要左窗口移动
while (windowMap.size() > 2){
int li = tree[left]; // 移除窗口的值
left++; // 左窗口右移
// 进行窗口内数据的一系列更新
int count = windowMap.get(li);
if (count > 1){
windowMap.put(li, windowMap.get(li) - 1);
}else {
windowMap.remove(li);
}
}
// 结果更新
res = Math.max(res, right - left);
}
return res;
}
5、No-repeat Substring (hard)
描述
给定一个字符串,请找出其中无重复字符的最长子字符串。
样例
样例 1:
输入: "abcabcbb"
输出: 3
解释: 最长子串是 "abc".
样例 2:
输入: "bbbbb"
输出: 1
解释: 最长子串是 "b".
public class Solution {
/**
* @param s: a string
* @return: an integer
*/
public int lengthOfLongestSubstring(String s) {
// write your code here
if (s.length() == 0)
return 0;
int res = 0;
char[] ch = s.toCharArray();
int left = 0;
int right = 0;
Map<Character, Integer> windowMap = new HashMap<>();
while (right < ch.length){
char rc = ch[right]; // 放入窗口的值
right++; // 窗口右移
// 进行窗口的数据的一系列操作
windowMap.put(rc, windowMap.getOrDefault(rc, 0) + 1);
// 判断左窗口是否要收缩
while (windowMap.get(rc) > 1){
char lc = ch[left]; // 从窗口移除的值
left++; // 左窗口右移
// 进行窗口的数据的一系列操作
int count = windowMap.get(lc);
if (count > 1){
windowMap.put(lc, windowMap.get(lc) - 1);
}else{
windowMap.remove(lc);
}
}
// 判断结果
res = Math.max(res, right - left);
}
return res;
}
}
6、Longest Substring with Same Letters after Replacement (hard)
描述
给定一个仅包含大写英文字母的字符串,您可以将字符串中的任何一个字母替换为的另一个字母,最多替换k次。 执行上述操作后,找到最长的,只含有同一字母的子字符串的长度。
字符串长度和k的大小不会超过10^4。
样例
样例1
输入:
"ABAB"
2
输出:
4
解释:
将两个'A’替换成两个’B’,反之亦然。
样例2
输入:
"AABABBA"
1
输出:
4
解释:
将中间的 'A’ 替换为 'B' 后得到 “AABBBBA"。
子字符串"BBBB" 含有最长的重复字符, 长度为4。
解题思路:来自:https://blog.csdn.net/qq_17550379/article/details/99309142
我们首先可以想到通过滑动窗口来做这个题目。我们首先有一个朴素的想法,就是窗口中的最多重复元素尽可能的多,基于此我们就需要遍历的过程中记录窗口里面出现的最多重复元素的个数。例如
A B A B B
↑ ↑
l r
123
此时窗口中的最多重复元素是A,并且它的个数是2。接着我们看一下移动窗口的过程中,如何去维护它。
我们假设k=1,那么此时需要替换的元素个数r-l+1-2=1,我们发现此时等于k,所以我们需要继续扩大窗口。
A B A B B
↑ ↑
l r
123
此时B出现了2次,那么最多重复元素是B(虽然B和A一样多,但是我们要最近出现的那个),并且r-l+1-2>k,所以我们需要缩小窗口
A B A B B
↑ ↑
l r
123
此时r-l+1-2=k,所以我们扩大窗口。
A B A B B
↑ ↑
l r
123
我们发现此时的B出现了3次,并且r-l+1-3=k满足条件,我们需要将此时的窗口大小记录下来。
1、窗口大小 - 出现最多的字符 = 变换的次数k 符合条件
2、窗口大小 - 出现最多的字符 > 变换的次数k 需要缩小窗口
3、窗口大小 - 出现最多的字符 < 变换的次数k 需要扩大窗口
public class Solution {
/**
* @param s: a string
* @param k: a integer
* @return: return a integer
*/
public int characterReplacement(String s, int k) {
// write your code here
if (s.length() == 0)
return 0;
int res = 0;
char[] ch = s.toCharArray();
int left = 0; // 左窗口指针
int right = 0; // 右窗口指针
Map<Character, Integer> windowMap = new HashMap<>(); // 窗口
int maxCount = 0; // 窗口中的匹配最多的字符的个数
while (right < ch.length){
char rc = ch[right]; // 进入右窗口的值
right++; // 右移
// 进行窗口内数据的一系列操作
windowMap.put(rc, windowMap.getOrDefault(rc, 0) + 1); // 加到窗口中
maxCount = Math.max(maxCount, windowMap.get(rc)); // 更新最多的字符的个数
// 判断是否需要缩小窗口 (这里是窗口中其他个数的字符大于 k 就缩小,以为可以替换 k 次)
while (right - left - maxCount > k){
char lc = ch[left]; // 移除窗口的值
left++; // 左窗口右移
// 进行窗口内数据的一系列操作
int count = windowMap.get(lc);
if (count > 0){
windowMap.put(lc, count - 1);
}else {
windowMap.remove(lc);
}
}
// 更新最多的结果
res = Math.max(res, right - left);
}
return res;
}
}