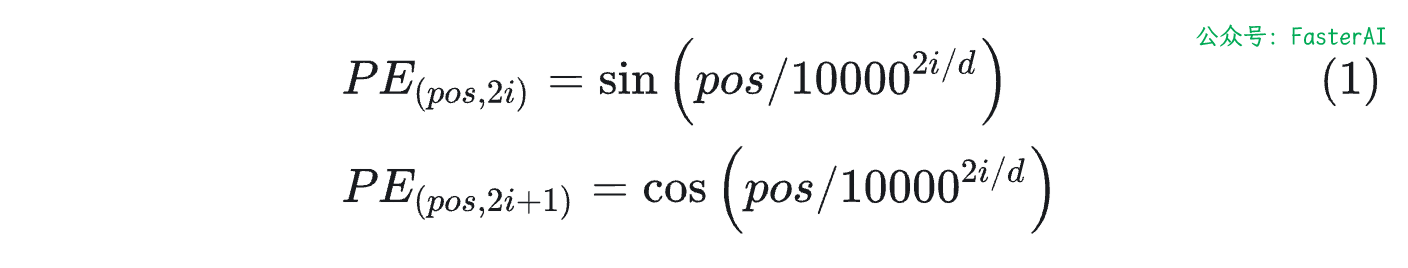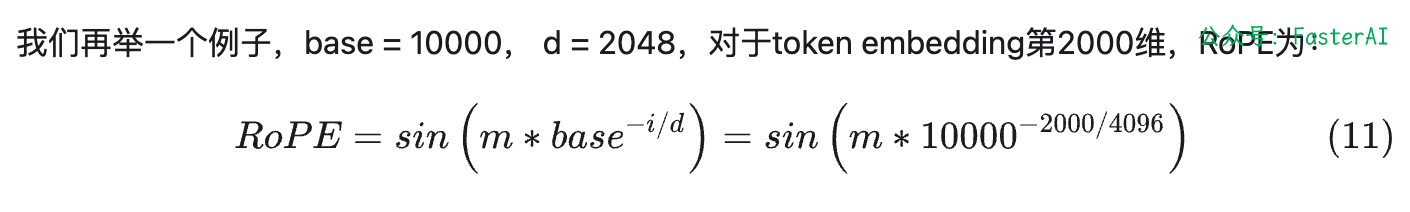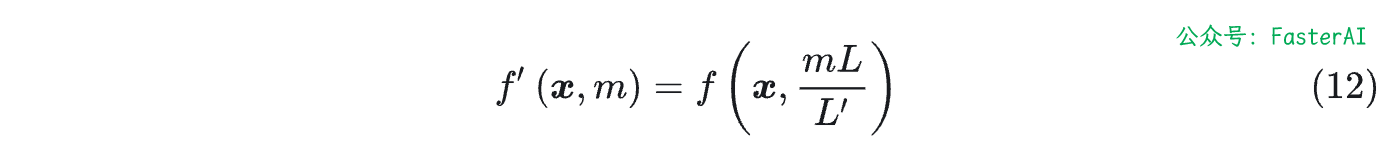【NLP高频面题 - LLM架构篇】旋转位置编码RoPE相对正弦位置编码有哪些优势?
重要性:⭐⭐⭐ 💯
NLP Github 项目:
-
NLP 项目实践:fasterai/nlp-project-practice
介绍:该仓库围绕着 NLP 任务模型的设计、训练、优化、部署和应用,分享大模型算法工程师的日常工作和实战经验
-
AI 藏经阁:https://gitee.com/fasterai/ai-e-book
介绍:该仓库主要分享了数百本 AI 领域电子书
-
AI 算法面经:fasterai/nlp-interview-handbook#面经
介绍:该仓库一网打尽互联网大厂NLP算法面经,算法求职必备神器
-
NLP 剑指Offer:https://gitee.com/fasterai/nlp-interview-handbook
介绍:该仓库汇总了 NLP 算法工程师高频面题
RoPE相对正弦位置编码而言是更好的位置编码方式。一个好的位置编码应该满足以下条件:
- 每个位置输出一个唯一的编码
- 具备良好的外推性
- 任何位置之间的相对距离在不同长度的句子中应该是一致的
RoPE可以更好的解决上面的三个问题。
正弦编码(Sinusoidal)
基于Sinusoidal的位置编码最初是由谷歌在论文Attention is All You Need中提出的方案,用于Transformer的位置编码。具体计算方式如下所示:
其中pos是位置,i表示维度。
- 具有相对位置表达能力:Sinusoidal可以学习到相对位置,对于固定位置距离的k,PE(i+k)可以表示成PE(i)的线性函数。
- 两个位置向量的内积只和相对位置 k 有关。
- Sinusoidal编码具有对称性。,即 P E ( t + k ) P E ( t ) = P E ( t ) P E ( t − k ) PE(t+k)PE(t) = PE(t)PE(t-k) PE(t+k)PE(t)=PE(t)PE(t−k),这表明Sinusoidal编码具有对称性。
- 随着k的增加,内积的结果会直接减少,即会存在远程衰减。
- 正弦编码是否真的具备外推性?实际的Attention计算中还需要与attention的权重W相乘,即 P E t T W q T W k P E t + k PE_t^T{W}_q^{T}{W}_kPE_{t+k} PEtTWqTWkPEt+k ,这时候内积的结果就不能反映相对距离
正弦编码是否真的具备外推性?
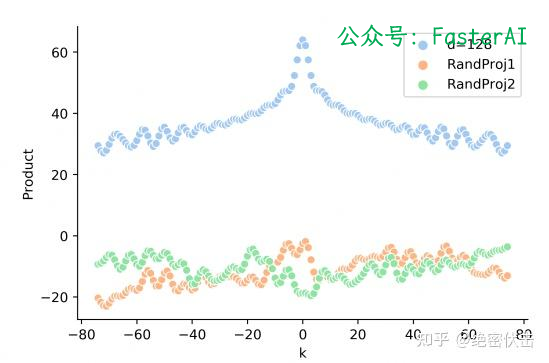
似乎Sinusoidal只和相对位置有关。但是实际的Attention计算中还需要与attention的权重W相乘,即 P E t T W q T W k P E t + k PE_t^T{W}_q^{T}{W}_kPE_{t+k} PEtTWqTWkPEt+k ,这时候内积的结果就不能反映相对距离。正弦编码中真实的q,k向量内积和相对距离之间,没有远程衰减性,如下图所示:
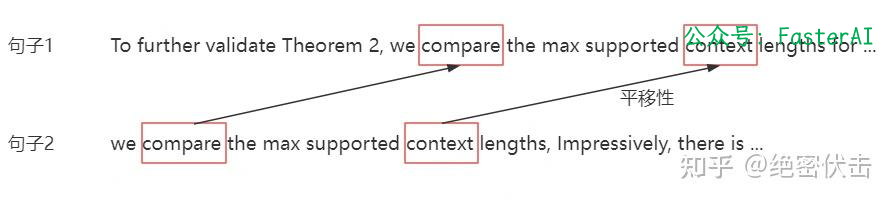
首先,对于RoPE编码任何位置之间的相对距离在不同长度的句子中应该是一致的。
如果两个token在句子1中的相对距离为k,在句子2中的相对距离也是k,那么这两个句子中,两个token之间的相关性应该是一致的,也就是attention_sample1(token1, token2) = attention_sample2(token1, token2)。
可以从旋转矩阵的角度轻松理解此特性。
其次:RoPE编码中q,k向量内积只和相对位置有关
最后,RoPE位置编码具有良好的外推性。
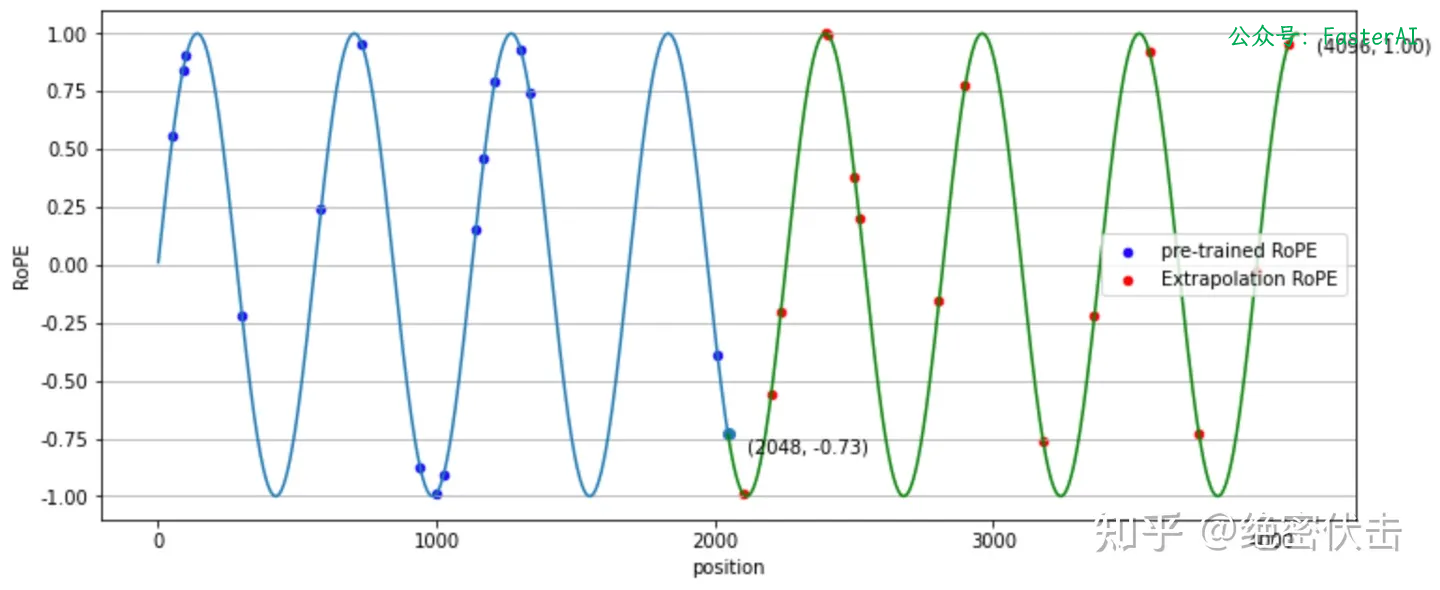
RoPE位置编码:
可以看出,在外推(Extrapolation)时,红色点超出了预训练时的位置编码。
为了解决这个问题,位置线性内插的核心思想是通过缩放位置索引,使得模型能够处理比预训练时更长的序列,而不损失太多性能。
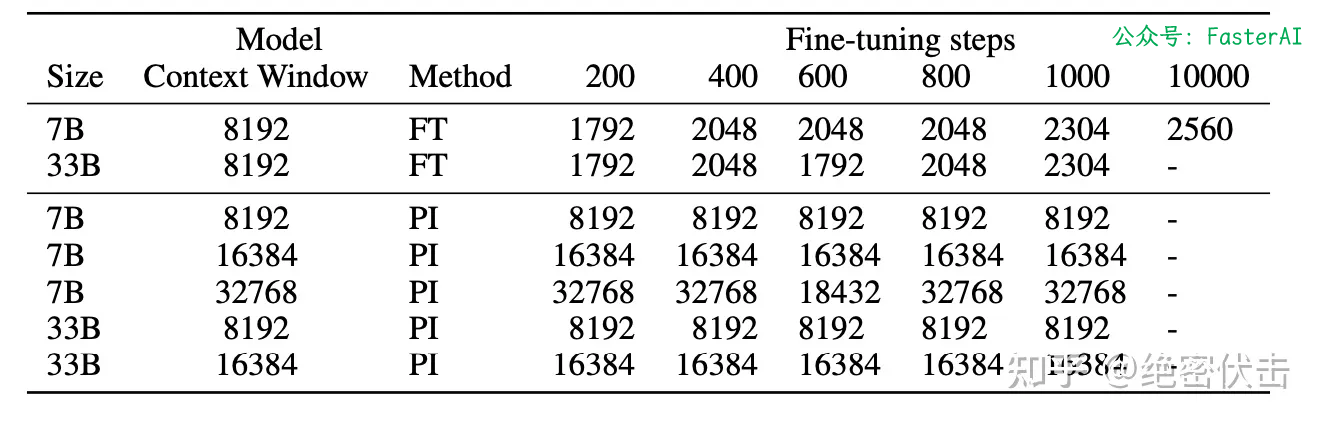
微调少量长文本,位置线性内插就能推理长文本:
另外,RoPE旋转位置编码不是作用在embedding的输入层,而是作用在与Attention的计算中,可以避免在输入中引入噪声。
NLP 大模型高频面题汇总
NLP基础篇
-
【NLP 面试宝典 之 模型分类】 必须要会的高频面题
-
【NLP 面试宝典 之 神经网络】 必须要会的高频面题
-
【NLP 面试宝典 之 主动学习】 必须要会的高频面题
-
【NLP 面试宝典 之 超参数优化】 必须要会的高频面题
-
【NLP 面试宝典 之 正则化】 必须要会的高频面题
-
【NLP 面试宝典 之 过拟合】 必须要会的高频面题
-
【NLP 面试宝典 之 Dropout】 必须要会的高频面题
-
【NLP 面试宝典 之 EarlyStopping】 必须要会的高频面题
-
【NLP 面试宝典 之 标签平滑】 必须要会的高频面题
-
【NLP 面试宝典 之 Warm up 】 必须要会的高频面题
-
【NLP 面试宝典 之 置信学习】 必须要会的高频面题
-
【NLP 面试宝典 之 伪标签】 必须要会的高频面题
-
【NLP 面试宝典 之 类别不均衡问题】 必须要会的高频面题
-
【NLP 面试宝典 之 交叉验证】 必须要会的高频面题
-
【NLP 面试宝典 之 词嵌入】 必须要会的高频面题
-
【NLP 面试宝典 之 One-Hot】 必须要会的高频面题
-
…