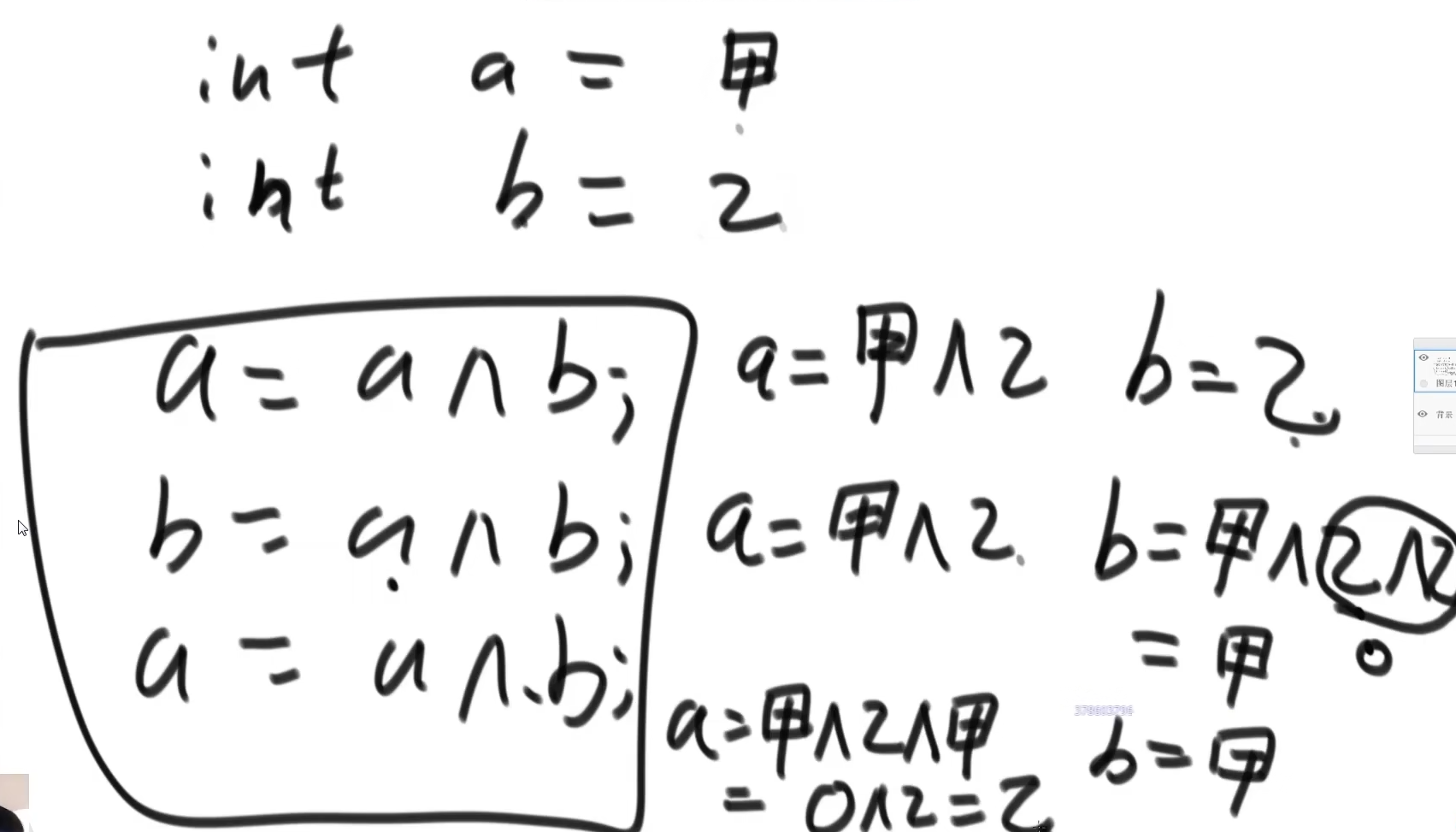排序算法

选择排序

时间复杂度：O(n^2)

• 将数组分成有序区和无序区。一开始整个数组是无序区。
• 每次从无序区中找到最小元素的下标，然后与无序区的第一个元素进行交换。

private static void selectionSort(int[] array){
    for (int i = 0; i < array.length; i++) {
        int min_idx = i;
        for (int j = i + 1; j < array.length; j++) {
            if (array[j] < array[min_idx]) {
                min_idx = j;
            }
        }
        int temp = array[i];
        array[i] = array[min_idx];
        array[min_idx] = temp;
    }
}

冒泡排序

时间复杂度：O(n^2)

• 每次从第 0 个元素开始，依次比较相邻的两个元素。如果后一个比前一个大，则进行交换。
• 之后的内循环比较次数，内循环的次数就会减一个，因为上一轮已经把最大的元素移动到了末尾。
• 优化：如果能够判断某一轮的内循环没有进行交换元素，则说明数组已经有序，则直接退出循环

private static void bubbling(int[] array){
    for (int i = 0; i < array.length; i++) {
        boolean flag = false;
        for (int j = 0; j < array.length - 1 - i; j++) {
            if(array[j] > array[j + 1]){
                flag = true;
                int temp = array[j];
                array[j] = array[j + 1];
                array[j + 1] = temp;
            }
        }
        if (!flag) {
            break;
        }
    }
}

插入排序

时间复杂度：O(n^2)

• 将数组分成有序区和无序区。一开始数组的第一个元素是有序区，后面都是无序区。
• 遍历无序区的元素，将插入插入到有序区对应的位置上。

private static void insertSort(int[] array){
    for (int i = 1; i < array.length; i++) {
        if(array[i] < array[i - 1]){
            int temp = array[i];
            int idx = i - 1;
            while(idx >= 0 && array[idx] > temp){
                array[idx + 1] = array[idx];
                idx--;
            }
            array[++idx] = temp;
        }
    }
}

二分查找

在一个有序数组中，找某个数是否存在

在一个有序数组中，找>=某个数最左侧的位置

34. 在排序数组中查找元素的第一个和最后一个位置

局部最小值问题

162. 寻找峰值

亦或（^）

性质：

1. 相当于无进位相加，1 + 0 = 1，1 + 1 = 0，0 + 0 = 0
2. 0 ^ n = n，n ^ n = 0
3. 满足交换律、结合律，a ^ b = b ^ a，(a ^ b) ^ c = a ^ (b ^ c)

应用：

不使用额外变量，交换两个变量的值

LCR 177. 撞色搭配

技巧：

只获得eor二进制最右边的1，其他位置设置为0
int rightOne = eor & (~eor + 1);